06-时间和因果关系

1 .CS 5412: Lecture 6 Timestamped Data Ken Birman Spring, 2019 http://www.cs.cornell.edu/courses/cs5412/2019sp 1

2 .Timestamps Last time we discussed time more as an active aspect of a coordinated system (one of a few dimensions in which an IoT system might be active). But once a sensor reading is captured and stored, there is also a temporal aspect to data analysis. What can we say about time for data and events “inside” a data store? http://www.cs.cornell.edu/courses/cs5412/2019sp 2

3 .Time in the real world Einstein was first to really look closely at this topic. It led to his theories of relativity and his Nobel Prize. But Einstein was thinking about particles moving at near the speed of light, or near black holes. Do those ideas apply in other settings? http://www.cs.cornell.edu/courses/cs5412/2019sp 3

4 .Time in computer Systems In IoT , time is tricky to work with for many reasons: Even with GPS recievers , it can be hard to get a good fix, so time can drift IoT sensors often lack GPS and their clocks need to be reset via an event, but then might drift by seconds per day Sensors can also fail, and this includes their clocks. Thus a timestamped event may have inaccurate time! http://www.cs.cornell.edu/courses/cs5412/2019sp 4 An early “integrated clock chip” (Wikipedia)

5 .In what ways can we talk about Time? First, whenever we use time in an IoT setting, it is important to track the time source and the associated skew: Without GPS time, sensor time will drift by seconds/day With GPS time, clocks can be accurate to within about 1ms With special purpose hardware for synchronization, the machines in a cloud would be able to share a clock and be accurate to a few us. … but today’s cloud computers don’t have that form of shared clocks, and if virtualized, clocks can be quite inaccurate! A total mess! http://www.cs.cornell.edu/courses/cs5412/2019sp 5

6 .vendors prefer limited accuracY ! Several recent security problems have involved an attacker who places a monitoring program on the same machine that some security code is on. The attacker is assumed to have the source code for the application it is attacking. The monitoring program measures timing properties of the memory and caching hardware at very high accuracy and is able to deduce contents of the memory state of the attacked program. It seems doubtful that this would work, but several exploits show that it really does work! Even so, cloud vendors make it hard to measure time. http://www.cs.cornell.edu/courses/cs5412/2019sp 6

7 .Lamport’s Causal Order Leslie Lamport is a famous distributed computing researcher Started out as a physicist and was inspired by Einstein, but went on to formalize distributed protocols, and won the Turing Award Primarily a theoretician, but he also was the author of Latex Especially good at elegant ways of posing problems and solving them He suggested that an important aspect of consistency should involve “consistency with respect to past events”. He calls this “causal” consistency http://www.cs.cornell.edu/courses/cs5412/2019sp 7 Drill down: C onsistency

8 .How does he define causality? Suppose that event A occurs in a data center, and then later event B. Did A “cause” B to happen? What if A was at 10am, and B at 11:30pm. Does knowing time help? What if A was a command to register a new student, and B was an internal action that creates her “meal card” account? What if A was an email from the department asking me about my teaching preferences, and B was my reply? http://www.cs.cornell.edu/courses/cs5412/2019sp 8 Drill down: C onsistency

9 .How does he define causality For Leslie, event A causes event B if there was a computation that somehow was triggered by A, and B was part of it. Inspired by physics! But this is hard to discover automatically. Instead, Leslie focused on potential causality: A “might” have caused B. Under what conditions is this possible? Somehow, information must flow from A to B. http://www.cs.cornell.edu/courses/cs5412/2019sp 9 Drill down: C onsistency

10 .Notation for representing causality Leslie proposes that we write A  B if A potentially caused B. He suggests that we use the words “happened before” for  Now the question arises: is  just a mathematical concept, or can we build a practical tool for tracking causality in real systems? http://www.cs.cornell.edu/courses/cs5412/2019sp 10 Drill down: C onsistency

11 .Why would we want to track A  B? Consider the Securities and Exchange Commission. For them, A might be “information about stock X” and B “a trade of X”. An insider trade occurs if someone with non-public information takes advantage to trade a stock before that information comes out. So if “John learned that the Lilly drug for Alzheimer’s showed promise”, then bought Lilly stock, perhaps John violated the insider trading law. http://www.cs.cornell.edu/courses/cs5412/2019sp 11

12 .Lamport’s point Simply seeing data records in which John talks to his friend at Lilly at 10:00am and then buys Lilly stock at 10:01am might not be “proof” of criminality. If the records were timestamped by the identical clock, and the clock isn’t faulty, this really would be proof. But if the records came from different computers, clock imprecision could be creating an illusion. If we track actual  , we would be confident. http://www.cs.cornell.edu/courses/cs5412/2019sp 12

13 .Tracking A  B Leslie first considered normal clocks. But they don’t track  Here, he took his inspiration from Einstein “ Time is an illusion.” Einstein went on to draw space-time diagrams. So Leslie asked: “Can we use space-time diagrams as the basis of a new kind of “logical clock”? If A  B, then LogicalClock (A) < LogicalClock (B) If LogicalClock (A) < LogicalClock (B), then A  B http://www.cs.cornell.edu/courses/cs5412/2019sp 13 Drill down: C onsistency

14 .Developing a solution Suppose that every computer (P, Q, …) has a local, private integer Call these LogicalClock P and LogicalClock Q etc. Each time something happens, increment the clock. Now, if A and B happen at P, the LogicalClock P can tell us that A  B. But what if A is on machine P, and B happens on Q? http://www.cs.cornell.edu/courses/cs5412/2019sp 14 Drill down: CAP C onsistency

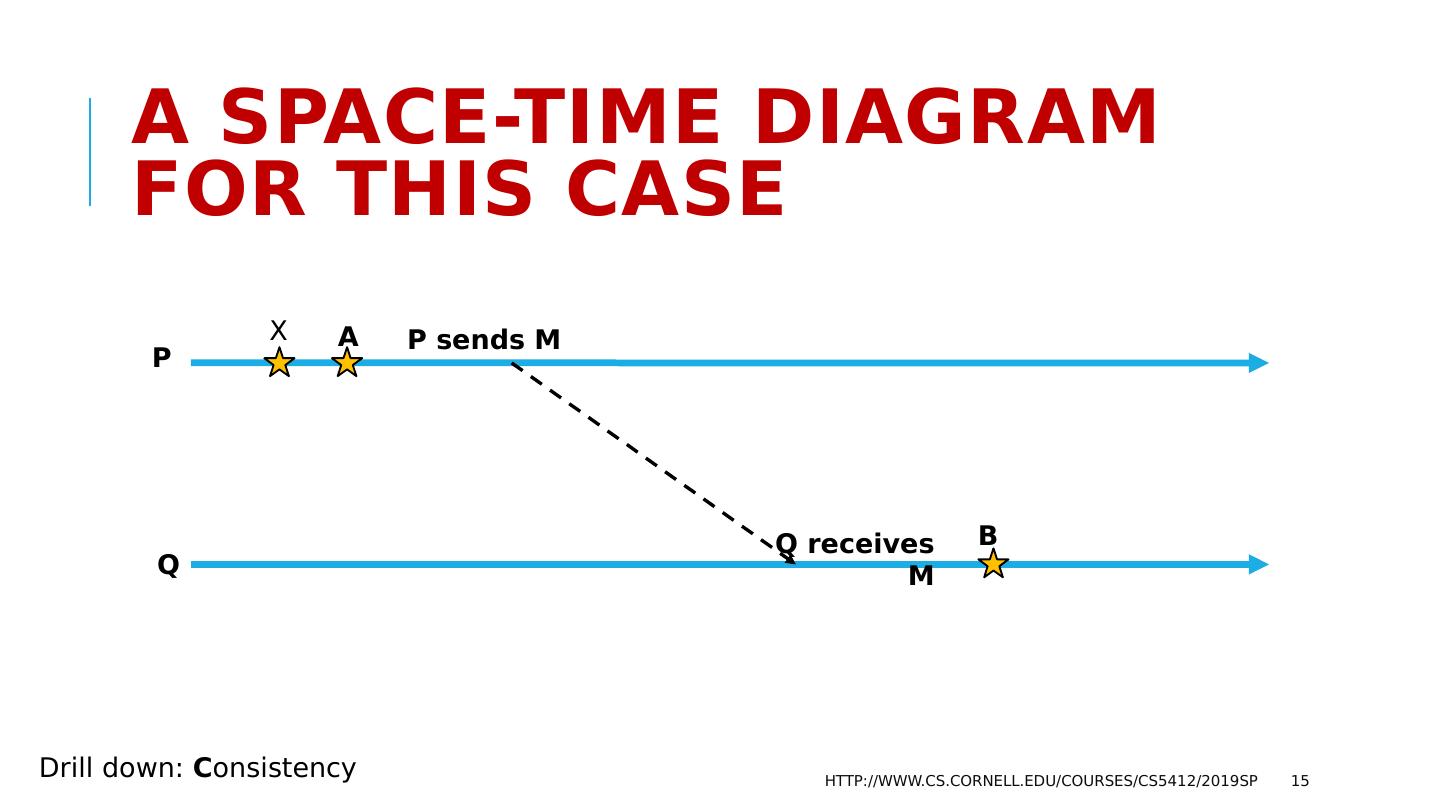
15 .A space-time Diagram for this case http://www.cs.cornell.edu/courses/cs5412/2019sp 15 P Q A B P sends M Q receives M Drill down: C onsistency X

16 .A space-time Diagram for this case Uncoordinated counters don’t solve our problem Here, A and B end up with the identical Time, so we incorrectly conclude that A did not happen before B http://www.cs.cornell.edu/courses/cs5412/2019sp 16 P LogicalClock P Q LogicalClock Q A P sends M 0 1 2 3 0 1 2 Q receives M B Drill down: C onsistency X

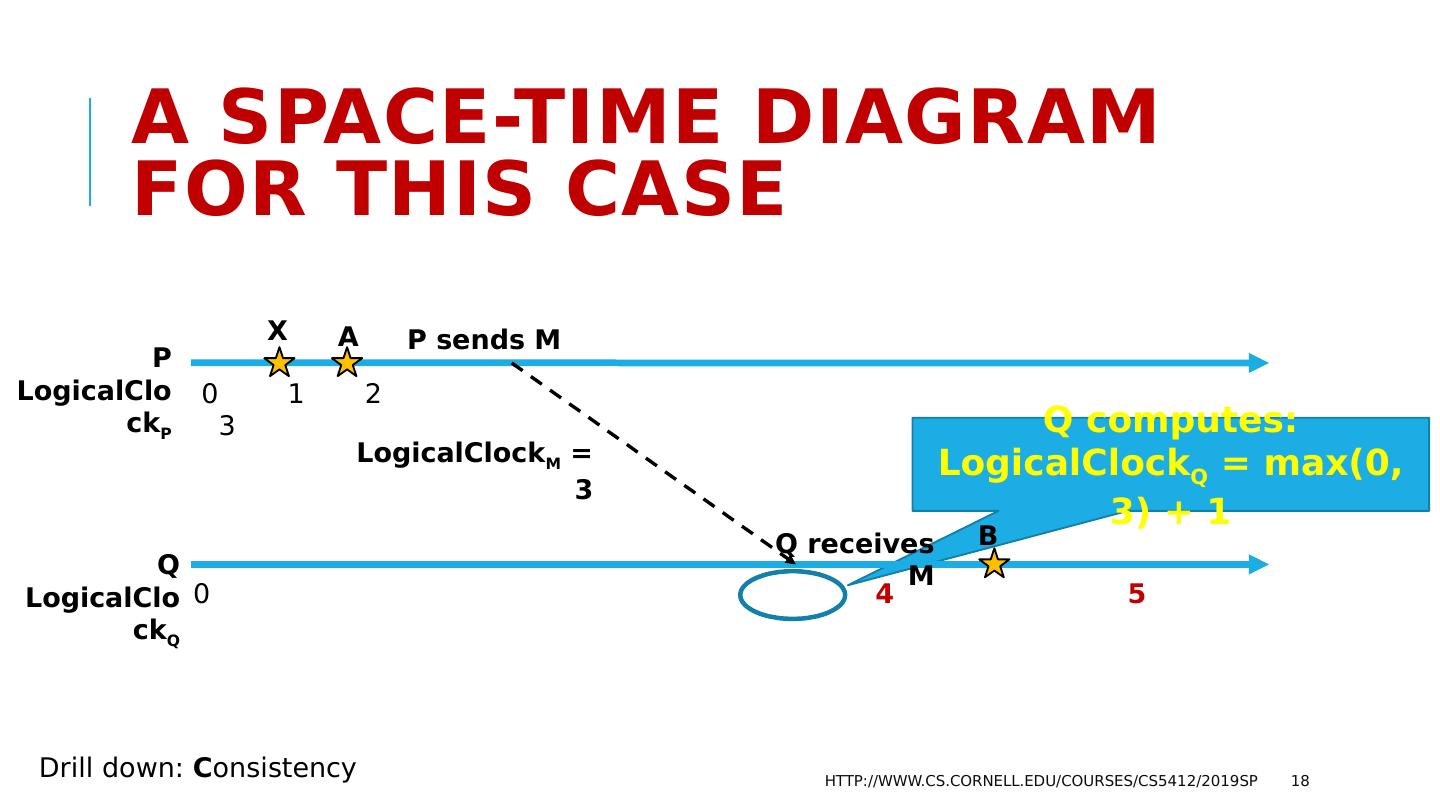
17 .Aha! But notice that in the diagram, the “receive” occurs when LogicalClock B  1. Yet the “send” of M was at LogicalClock A  3. So Lamport proposes this fix: Each time an interesting event occurs at P, increment LogicalClock P If P sends M to Q, include LogicalClock P in M. When Q receives M, LogicalClock Q = Max( LogicalClock Q , LogicalClock M ) + 1 http://www.cs.cornell.edu/courses/cs5412/2019sp 17 Drill down: C onsistency

18 .Q computes: LogicalClock Q = max(0, 3) + 1 A space-time Diagram for this case http://www.cs.cornell.edu/courses/cs5412/2019sp 18 P LogicalClock P Q LogicalClock Q A P sends M 0 1 2 3 0 4 5 Q receives M B Drill down: C onsistency LogicalClock M = 3 X

19 .We now have a cheap partial solution! With Lamport’s logical clocks, we pay a small cost (one integer per machine, to keep the clock, and some space in the message) Let’s use Time(X) to denote the relevant LogicalClock value for x. We can time-stamp events and messages. If A  B, then Time(A) < Time(B) But… if Time(A) < Time(B), perhaps A didn’t happen before B! http://www.cs.cornell.edu/courses/cs5412/2019sp 19 Drill down: C onsistency

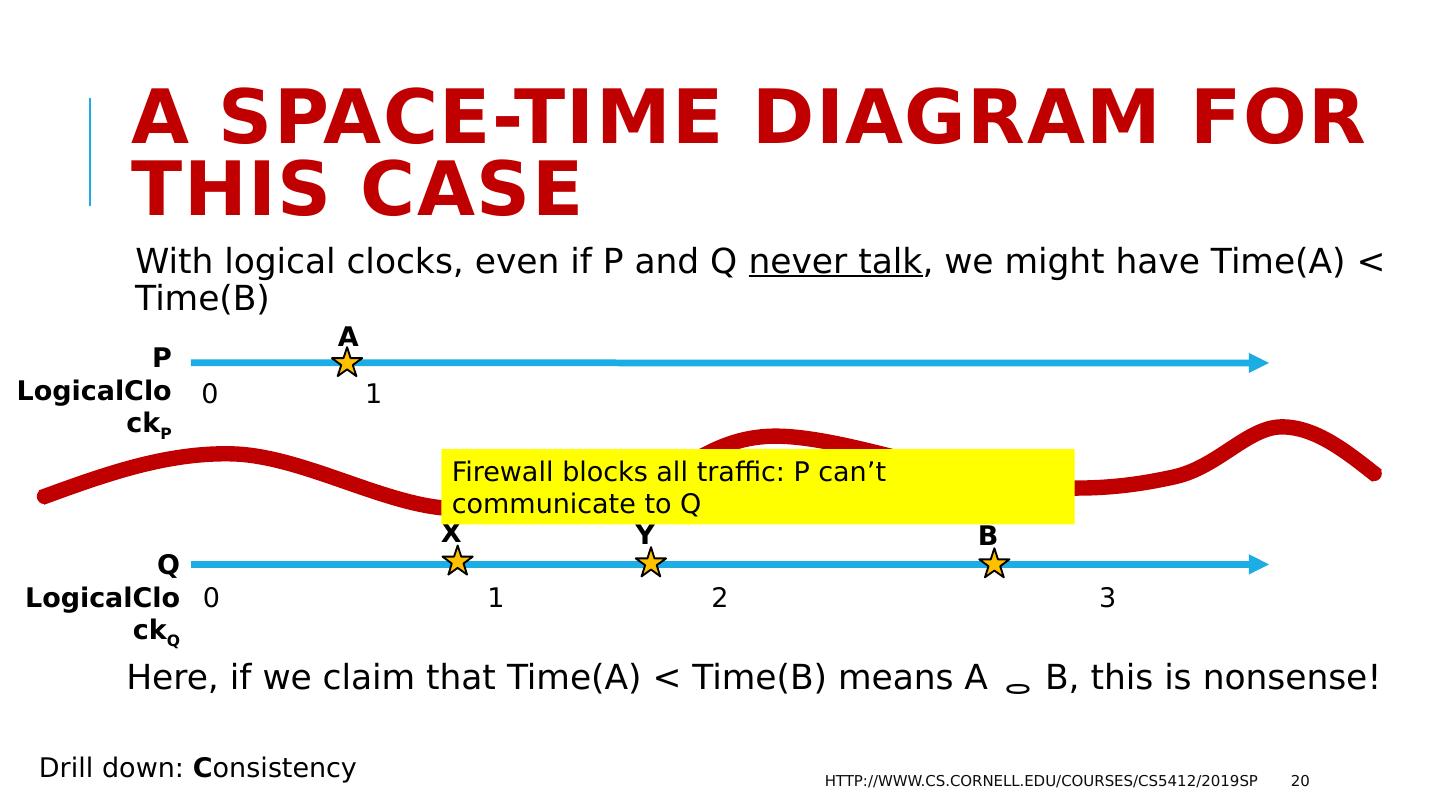
20 .A space-time Diagram for this case With logical clocks, even if P and Q never talk , we might have Time(A) < Time(B) Here, if we claim that Time(A) < Time(B) means A  B, this is nonsense! http://www.cs.cornell.edu/courses/cs5412/2019sp 20 P LogicalClock P Q LogicalClock Q A 0 1 0 1 2 3 B X Y Drill down: C onsistency Firewall blocks all traffic: P can’t communicate to Q

21 .Logical clocks only work in one direction. They approximate the causal happens-before relationship, but only in an “if-then” sense, not “If and only if”. Lamport gives many examples where this is good enough. We actually can do better, but at the “cost” of higher space overhead. http://www.cs.cornell.edu/courses/cs5412/2019sp 21 Drill down: C onsistency

22 .Would a logical Clock work for the SEC? The SEC wants to detect that “John learned of the good news from Lilly, then purchased stock before the market heard.” If A was John learning, and B was the stock purchase, then the SEC wants to look at TimeStamp (A) < TimeStamp (B), and conclude “A  B”. Logical Clocks don’t have this specific property! So we can’t use them to solve this SEC monitoring goal. http://www.cs.cornell.edu/courses/cs5412/2019sp 22

23 .Intuition behind vector clocks Suppose that we had a fancier clock that could act like logical clocks do (with the “take the max, then add one” rule). But instead of a single counter, what if it were to count “events in the causal past of this point in the execution”, tracking events on a per-process basis? For example, a VectorClock value for A = [5,7] might mean “event A happens after 5 events at P, and 7 events at Q”. http://www.cs.cornell.edu/courses/cs5412/2019sp 23

24 .Vector Clocks are easy to implement A vector clock has one entry per machine. VT(A) = [3, 0, 7, 1] If an event occurs at P, P increments its own entry in the vector When Q receives M from P, Q computes an entry-by-entry max, then increments its own entry (because a “receive” is an event, too) VectorClock comparison rule: Define VT(A) < VT(B) if VT(A) ≤ VT(B), Now, VT(A) < VT(B) iff A  B but VT(A) ≠ VT(B) http://www.cs.cornell.edu/courses/cs5412/2019sp 24 Drill down: C onsistency

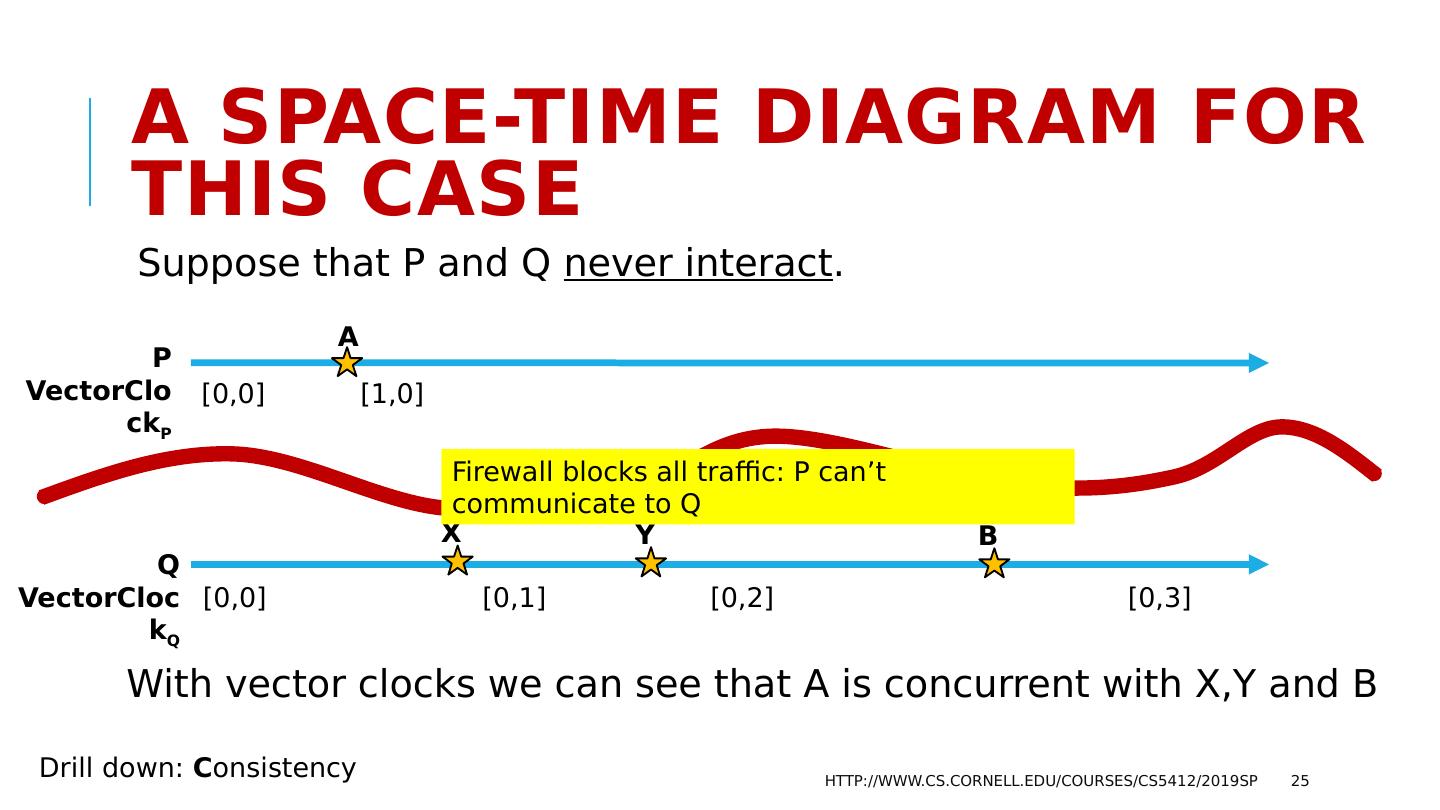
25 .A space-time Diagram for this case Suppose that P and Q never interact . With vector clocks we can see that A is concurrent with X,Y and B http://www.cs.cornell.edu/courses/cs5412/2019sp 25 P VectorClock P Q VectorClock Q A [0,0] [1,0] [0,0] [0,1] [0,2] [0,3] B X Y Drill down: C onsistency Firewall blocks all traffic: P can’t communicate to Q

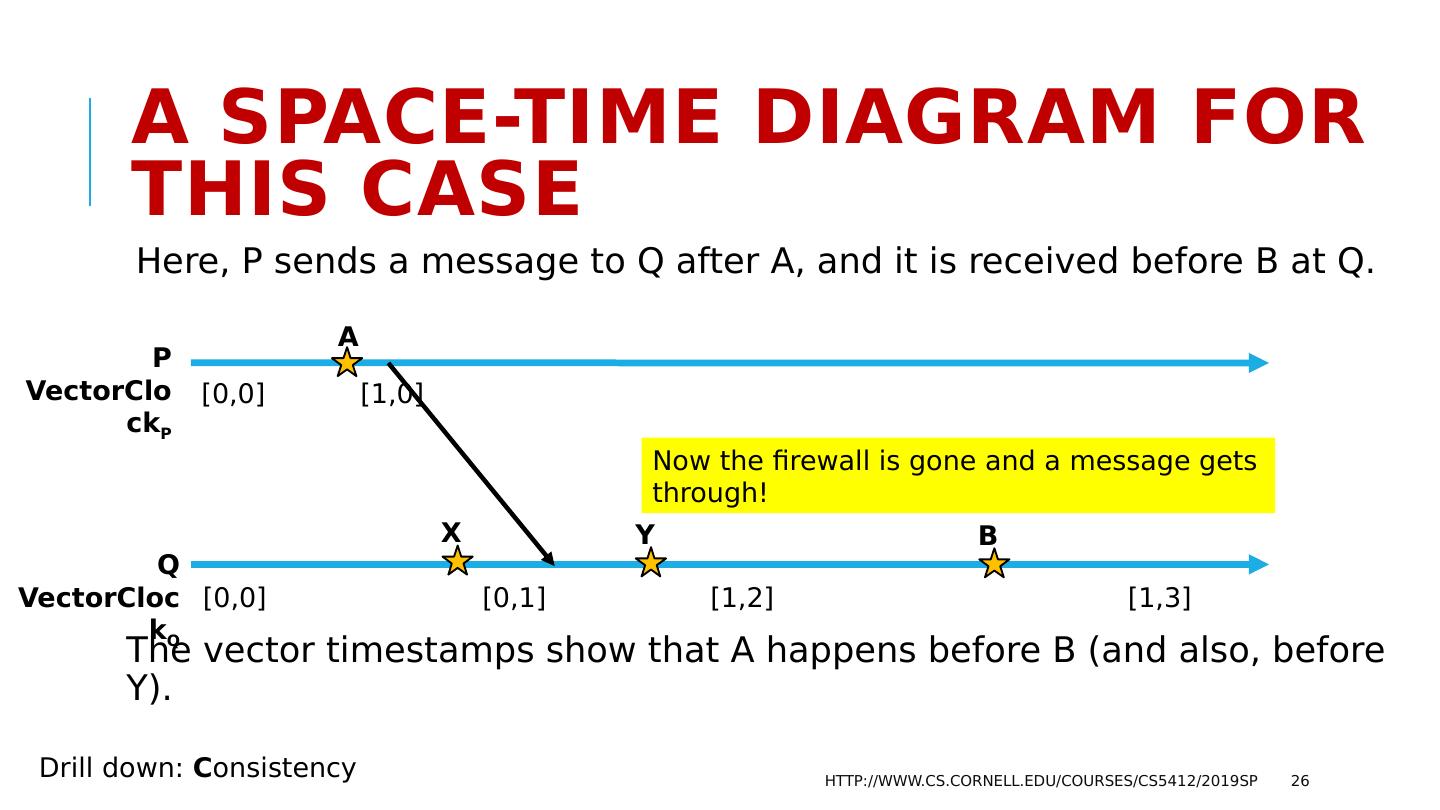
26 .A space-time Diagram for this case Here, P sends a message to Q after A, and it is received before B at Q. The vector timestamps show that A happens before B (and also, before Y). http://www.cs.cornell.edu/courses/cs5412/2019sp 26 P VectorClock P Q VectorClock Q A [0,0] [1,0] [0,0] [0,1] [1,2] [1,3] B X Y Drill down: C onsistency Now the firewall is gone and a message gets through!

27 .Vector Clocks solve the SEC problem! A: John spoke to his friend at Lilly. Then the message M was to tell his stock broker to “Buy Lilly futures ASAP!” B was the purchase. Our goal: Deduce that A  B using just a database with information about A, and information about B, including timestamps. We just saw that VectorClock (A) < VectorClock (B)  A  B! http://www.cs.cornell.edu/courses/cs5412/2019sp 27

28 .So why not always use vector clocks? They represent happens-before with full accuracy, which is great. But you need one vector entry per process in your application. For a small -service this would be fine, but if the vector would become large, the overheads are an issue. So, we try to use a LogicalClock before considering a VectorClock . http://www.cs.cornell.edu/courses/cs5412/2019sp 28

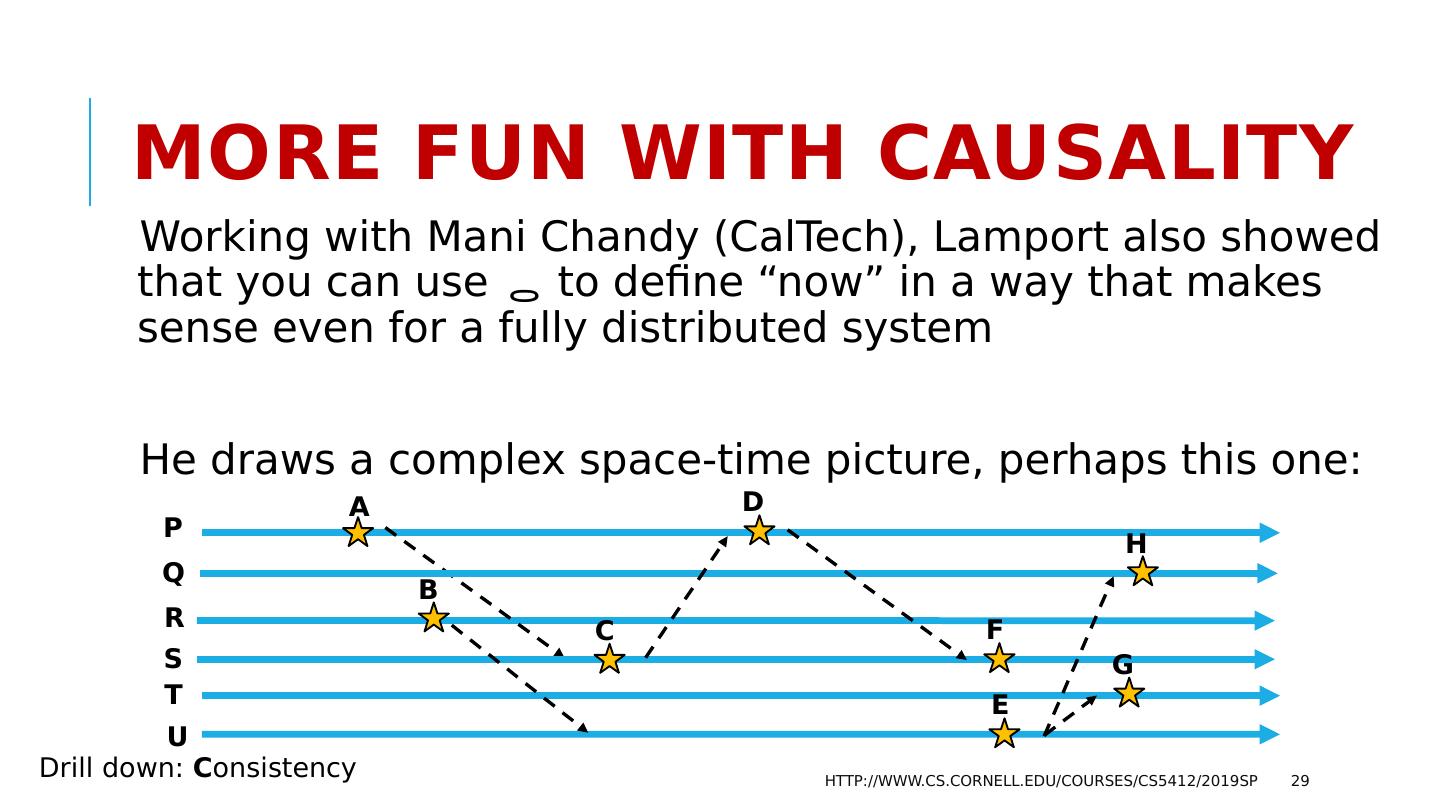
29 .More fun with Causality Working with Mani Chandy ( CalTech ), Lamport also showed that you can use  to define “now” in a way that makes sense even for a fully distributed system He draws a complex space-time picture, perhaps this one: http://www.cs.cornell.edu/courses/cs5412/2019sp 29 P Q A E F R S T U B D C H G Drill down: C onsistency