13-物联网的BlockChains

1 .CS5412/Lecture 13 Blockchains for I o T (Part 1) Ken Birman CS5412 Spring 2019 http://www.cs.cornell.edu/courses/cs5412/2019sp 1

2 .Blockchains for I o T What is blockchain? The most disruptive tech in decades ! “The distributed ledger technology, better known as blockchain, has the potential to eliminate huge amounts of record-keeping, save money and disrupt IT in ways not seen since the internet arrived.” Lucas Mearian , ComputerWorld Staff Writer http://www.cs.cornell.edu/courses/cs5412/2019sp 2 Lucas Mearian . Not afraid of hyperbole!

3 .A more technical answer? “A blockchain, originally block chain, is a growing list of records, called blocks, which are linked using cryptography. Each block contains a cryptographic hash of the previous block, a timestamp, and transaction data (generally represented as a Merkle Tree root hash). By design, a blockchain is resistant to modification of the data.” Wikipedia http://www.cs.cornell.edu/courses/cs5412/2019sp 3

4 .Terminology In BlockChain settings, a transaction is a digital record describing some event. Some transactions are complete and self-contained. But BlockChain also supports transaction languages in which one transaction might refer to events defined by a past or future transaction. http://www.cs.cornell.edu/courses/cs5412/2019sp 4

5 .Cryptographic Hash A cryptographic hash is a bit string computed from some block of data in a manner that yields a constant-length result irrespective of the data size, and yet such that it would be infeasible to find other data that would hash to the same result. There are a number of hashing schemes. A highly robust one is SHA-256. SHA-512 is even stronger. MD5 and SHA-1 have been compromised and are unsafe. http://www.cs.cornell.edu/courses/cs5412/2019sp 5

6 .Even faster hash methods exist http://www.cs.cornell.edu/courses/cs5412/2019sp 6 (single core performance, all Golang implementations, see benchmark ). BenchmarkHighwayHash 11,986 MB/s BenchmarkSHA256_AVX512 3,552 MB/s BenchmarkBlake2b 972 MB/s BenchmarkSHA1 950 MB/s (insecure) BenchmarkMD5 684 MB/s (insecure) BenchmarkSHA512 562 MB/s BenchmarkSHA256 383 MB/s Note: the AVX512 version of SHA256 uses the multi-buffer crypto library technique as developed by Intel, more details can be found in sha256-simd . https://blog.minio.io/highwayhash-fast-hashing-at-over-10-gb-s-per-core-in-golang-fee938b5218a

7 .Hardware can get even further FPGA and ASIC solutions can be purchased that will run SHA-256 or SHA-512 at speeds of 25,000 to 30,000 MB/s In some parts of the world there are entire datacenters equipped with huge numbers of these accelerator solutions. China dominates the business. Very hard to be a BlockChain miner with a single desktop computer today! http://www.cs.cornell.edu/courses/cs5412/2019sp 7

8 .Cryptographic hash Key All of these functions require a key in addition to the message. If the key is public, anyone can recompute the same hash from the message. If the key is private, then only the application holding the key can do so. The hash can then serve as a form of signature, verifiable by other components of the same application, since they would also know the key. http://www.cs.cornell.edu/courses/cs5412/2019sp 8

9 .Public/Private Key Pair (normally, RSA) This is a classic cryptographic method. RSA creates two “keys”, both just long numbers together with a modulus n that itself is a product of two very long prime numbers. Call them K, One is designated as the public key and shared. You keep the other private. http://www.cs.cornell.edu/courses/cs5412/2019sp 9 RSA K (RSA K (X)) = RSA K (RSA K (X)) = X

10 .Why RSA works In RSA encryption and decryption are just mathematical steps that involve a form of “ bignum ” arithmetic (modular exponentiation), performed block by block. RSA is secret because there is no known method for factoring a giant composite number that might have 1000’s of binary digits. If we could factor the modulus, it would be trivial to recover the secret key from the public one. Quantum computers might offer a path to doing so, but it would require devices with millions of qbits , way beyond anything feasible anytime soon. http://www.cs.cornell.edu/courses/cs5412/2019sp 10 In 1796, Gauss came up with the theory that ultimately gave us the (very simple) RSA technology. Gauss himself didn’t suggest this application.

11 .RSA strengths, weaknesses Very widely supported, basis of most “certificates” used in the Internet. Many tricks exist, based on commutativity of RSA computation. Basically, for any two RSA keys, A and B, RSA A (RSA B (M)) = RSA B (RSA A (M)). But RSA is fairly slow. The speed is a function of the data size. We don’t casually encrypt entire messages with RSA: it would be feasible but slow. http://www.cs.cornell.edu/courses/cs5412/2019sp 11

12 .How would process P sign message M? Compute the SHA-256 hash of M using a public SHA key. Now use P’s private key to encrypt the hash: SHA(M) private-key-of-P Process Q can easily verify that M has not been tampered with: Q recomputes the SHA-256 hash for M, using the same public SHA key Now Q uses RSA with P’s public key to crypt P’s signature. If they match, then Q has confirmed that M hasn’t changed. http://www.cs.cornell.edu/courses/cs5412/2019sp 12

13 .Notarizing blinded data There is even a method, by David Chaum , for signing an object that the signatory cannot see. It would be useful for secure voting: Prepare your ballot, then blind it and obtain a signature. The signature is proof that your vote was valid and only cast once. Submit it for counting now, unblinded, via a secure anonymous “onion route” The ballot itself has no identifying information, and neither does the signature. So a third party can see that your vote is valid, and can count it, and yet can’t learn how any particular individual voted. Chaum also showed how to get a receipt which can be used to be sure your vote was properly tabulated. http://www.cs.cornell.edu/courses/cs5412/2019sp 13

14 .Parallelism? A further win is to maximize parallelism and reduce record sizes. In the case of BlockChain , each block contains a set of transactions represented as binary records. These records might be huge, hence slow to hash (and very slow to encrypt, were you to try that). By having the creator store the record someplace reasonable and then just storing signatures in the BlockChain , we use it as efficiently as possible. http://www.cs.cornell.edu/courses/cs5412/2019sp 14

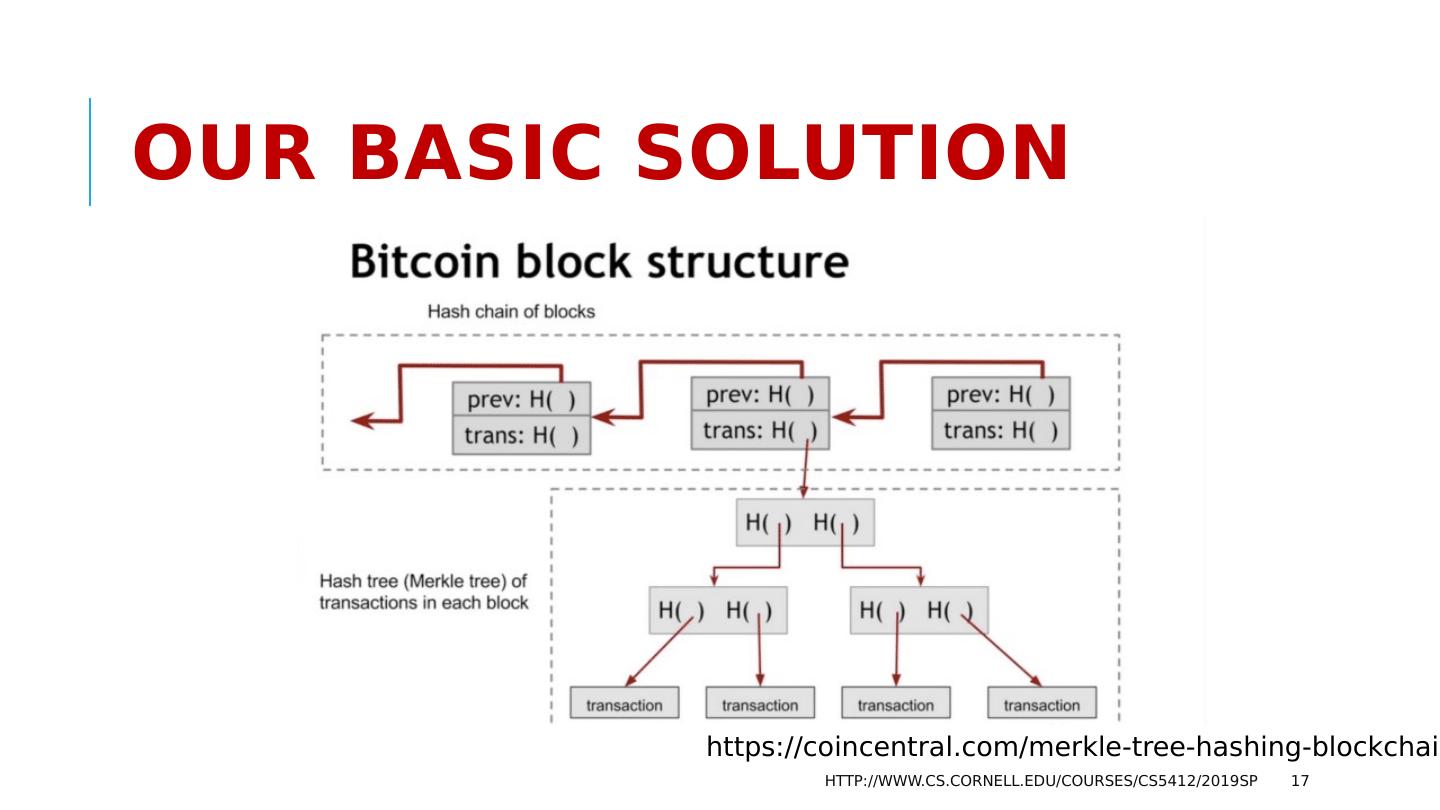
15 .Merkle Tree: A tree of signed records. Rather than making one list of N records and then hashing them, we often create a binary tree of hashes. Very common in BlockChains , permits us to run SHA-256 or SHA-512 in its fastest “mode” of operation. http://www.cs.cornell.edu/courses/cs5412/2019sp 15

16 .This already gives us a basic solution! Compute a series of records, each containing transactions signed by the initiator. The record needs to include the “name” of the initiator so that anyone needing to do so can look up the matching public key. The records would be a Merkle Tree of these transactions. Now to append record R to a chain with blocks B 0 … B k , take the signature from the root of the Merkle tree of R and hash it with the signature on B k . Store this hash into what will become B k+1 http://www.cs.cornell.edu/courses/cs5412/2019sp 16

17 .Our basic solution http://www.cs.cornell.edu/courses/cs5412/2019sp 17 https://coincentral.com/merkle-tree-hashing-blockchain/

18 .Why is this secure? If anyone tampers with any record in the chain, we can sense this by recomputing the Merkle tree. The signature won’t match. To verify the entire chain, block by block recompute the Merkle tree, then recompute the sequence of pairwise hash values. Verification is required when an untrusted BlockChain is initially loaded. http://www.cs.cornell.edu/courses/cs5412/2019sp 18

19 .Permissioned/ Permissionless BlockChain solutions split into two categories. A permissioned BlockChain is managed by an authorized group of servers, for example inside some datacenter. We generally assume that attackers either compromise the entire data center, or can’t attack the servers. A permissionless BlockChain is managed by an anonymous group of servers that volunteer to play the role, and might come and go at will. http://www.cs.cornell.edu/courses/cs5412/2019sp 19

20 .Permissionless Attacks are an issue! Permissionless BlockChain can come under many forms of attack. Compromised server might try to hand out “fake” versions of the chain. It might try to generate huge rates of transactions on its own, and not include your transactions. This is a form of DDoS attack. It could try to corrupt individual transactions or records. http://www.cs.cornell.edu/courses/cs5412/2019sp 20

21 .Proof Of Work A Proof of Work mechanism adds one more field to the blocks: a “nonce”. The nonce is just a bit string of some size. The rule is that to append B k+1 to the chain, in addition to hashing it with the hash of the prior block, P must also find a nonce such that when the nonce is included and a new hash is computed, the hash value ends with some desired number of 0 bits. http://www.cs.cornell.edu/courses/cs5412/2019sp 21

22 .Proof of work Finding such a nonce is hard work! So while P could be keen to append its block, it may need to search for this nonce for many seconds or minutes. The difficulty of finding a nonce value that will work prevents DDoS attacks. http://www.cs.cornell.edu/courses/cs5412/2019sp 22

23 .How most BlockChains Work today You can download the software as a VM or even compile it yourself. You launch the code on your own servers – this makes you a “miner” as soon as the system has initialized itself. The system downloads the entire current BlockChain , from other machines already running the BlockChain software (there is a web site listing some you can contact for copies). http://www.cs.cornell.edu/courses/cs5412/2019sp 23

24 .Next, you verify the BlockChain You’ll need to recompute all the Merkle trees and the chain of hashes. In fact this may not take enormously long… today. Few BlockChains have huge amounts of content. But someday, we might have BlockChains with hundreds of billions of records and total sizes in the petabytes. Then download speed and verification time and storage will become an issue! http://www.cs.cornell.edu/courses/cs5412/2019sp 24

25 .Meanwhile, new blocks arrive Each block extends some specific sequence of prior blocks. If you turn out to have downloaded the wrong sequence, you may have to truncate your chain and download the longer sequence. This is a “rollback”. During startup, substantial rollbacks can occur. Later they shouldn’t (assumes a fully connected network of mostly “correct” miners). http://www.cs.cornell.edu/courses/cs5412/2019sp 25

26 .At this point you can create transactions So, you open for business. Someone shows up to buy a glass of your fresh lemonade. You’ll generate the transaction (think “credit card payment slip”) and submit it to the system. It enters a pool of pending transactions. http://www.cs.cornell.edu/courses/cs5412/2019sp 26

27 .When will your transaction go through? Within an hour or so, you should see that your transaction got included into some block, and also that everyone seems to have adopted that block. The chain has moved six or more blocks into the future. So now you can hand that glass of frosty bliss to your happy customer! http://www.cs.cornell.edu/courses/cs5412/2019sp 27

28 .But nobody can cheat! To modify a past record you need to also modify every signature subsequent to that record. The step where you have to find these nonce values will be very slow and you’ll lose the race. http://www.cs.cornell.edu/courses/cs5412/2019sp 28 https://medium.com/loom-network/

29 .What if the attacker is a country? A country could build whole datacenters, equipped with hardware to compute SHA-256 at ultra-high speeds. In this case P (using the datacenter) could generate a lot of blocks quickly, for which they would be paid. Or could have an entire second BlockChain starting from months ago, and longer than the official main one. To prevent most such attacks, BlockChain solutions make the proof-of-work task harder as a function of the rate at which blocks are being found. http://www.cs.cornell.edu/courses/cs5412/2019sp 29