K-Means Segmentation - University of Missouri

1 .K-Means Segmentation 

2 .Segmentation 

3 . * * Pictures from Mean Shift: A Robust Approach toward Feature Space Analysis, by D. Comaniciu and P. Meer http://www.caip.rutgers.edu/~comanici/MSPAMI/msPamiResults.html 

4 . Segmentation and Grouping • Motivation: not • Grouping (or clustering) information is evidence – collect together tokens • Obtain a compact that “belong together” representation from an • Fitting image/motion – associate a model with sequence/set of tokens tokens – issues • which model? • Should support • which token goes to application which element? • Broad theory is absent • how many elements in the model? at present 

5 . General ideas • tokens – whatever we need to • bottom up group (pixels, points, surface elements, etc., segmentation etc.) – tokens belong together because they are locally • top down segmentation coherent – tokens belong together because they lie on the • These two are not same object mutually exclusive 

6 .Why do these tokens belong together?  

7 .

8 . Basic ideas of grouping in humans • Figure-ground • Gestalt properties discrimination – elements in a collection of elements can have – grouping can be seen in properties that result terms of allocating from relationships some elements to a (Muller-Lyer effect) figure, some to ground • gestaltqualitat – impoverished theory – A series of factors affect whether elements should be grouped together • Gestalt factors 

9 .

10 .

11 .

12 .

13 .

14 .

15 .

16 .Groupings by Invisible Completions 

17 .Here, the 3D nature of grouping is apparent: Why do these tokens belong together?  Corners and creases in 3D, length is interpreted differently: In The (in) line at the far end of corridor must be longer than the (out) near line if they measure to be the same size Out University of Missouri at Columbia 

18 .

19 .And the famous invisible dog eating under a tree: 

20 .A Final Example 

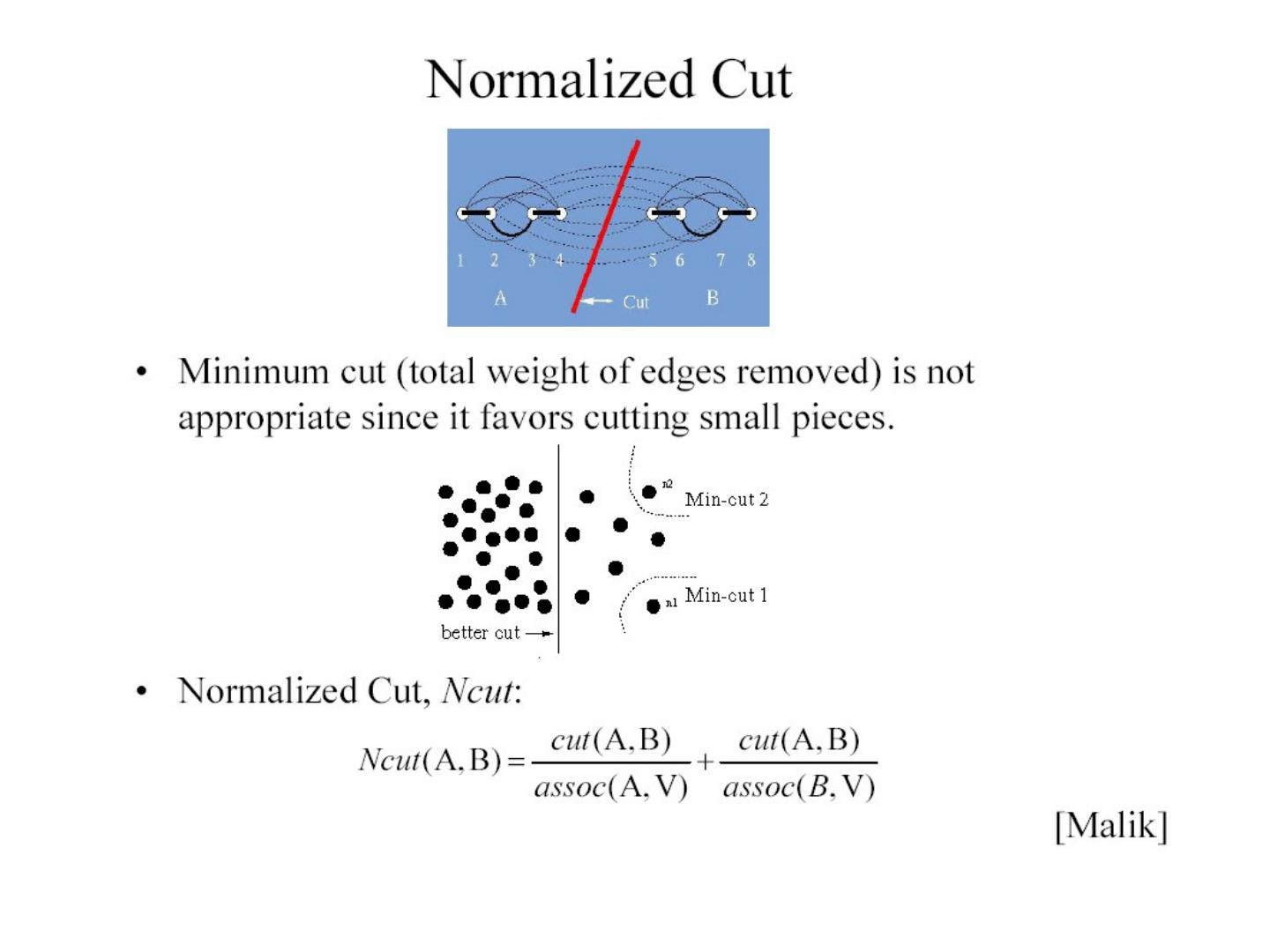
21 . Segmentation as clustering • Cluster together (pixels, tokens, etc.) that belong together • Point-Cluster distance • Agglomerative clustering – single-link clustering – attach closest to cluster it is – complete-link clustering closest to – group-average clustering – repeat • Dendrograms • Divisive clustering – yield a picture of output as – split cluster along best clustering process continues boundary – repeat 

22 .Simple clustering algorithms 

23 .

24 . K-Means • Choose a fixed number of clusters • Algorithm – fix cluster centers; • Choose cluster centers allocate points to and point-cluster closest cluster allocations to minimize – fix allocation; compute error best cluster centers • can’t do this by search, • x could be any set of because there are too features for which we many possible can compute a distance allocations. (careful about scaling)  2     x j   i  iclusters  jelements of i'th cluster  * From Marc Pollefeys COMP 256 2003 

25 .K-Means 

26 .K-Means * From Marc Pollefeys COMP 256 2003 

27 . Image Segmentation by K-Means • Select a value of K • Select a feature vector for every pixel (color, texture, position, or combination of these etc.) • Define a similarity measure between feature vectors (Usually Euclidean Distance). • Apply K-Means Algorithm. • Apply Connected Components Algorithm. • Merge any components of size less than some threshold to an adjacent component that is most similar to it. * From Marc Pollefeys COMP 256 2003 

28 .Results of K-Means Clustering: Image Clusters on intensity Clusters on color K­means clustering using intensity alone and color alone 

29 . K-Means • Is an approximation to EM – Model (hypothesis space): Mixture of N Gaussians – Latent variables: Correspondence of data and Gaussians • We notice: – Given the mixture model, it’s easy to calculate the correspondence – Given the correspondence it’s easy to estimate the mixture models