拟合优度检验

1 .7-3: 假设检验 张伟平 

2 .第七讲: 假设检验 7.3 拟合优度检验 . . . . . . . . . . . . . . . . . . 1 7.3.1 离散总体情形 . . . . . . . . . . . . . . 2 7.3.2 列联表的独立性和齐一性检验 . . . . . 8 7.3.3 连续总体情形 . . . . . . . . . . . . . . 12 Previous Next First Last Back Forward 1 

3 . 7.3 拟合优度检验 前面的假设检验基本上是在假定总体是正态的条件下做的, 但是 这个假设本身不一定成立, 需要收集样本 (X1 , · · · , Xn ) 来检验它. 一 般地, 检验 H0 : X服从某种分布F 可以采用 Karl Pearson 提出的 χ2 拟合优度检验. 基本想法: 基于样本得到 F 的估计 Fˆn , 计算某种偏差 D(Fˆn , F ), 例如 supx∈R |Fˆn (x) − F (x)|. 当 H0 正确时, 由于 Fˆn 是 F 的相合估 计, 偏差 D(Fˆn , F ) 应该很小. Karl Pearson 对离散分布 F 提出一种检验方法, 即拟合优度 检验方法或者称为 Pearson 卡方检验方法. Previous Next First Last Back Forward 1 

4 .7.3.1 离散总体情形 (1) 理论总体分布不含未知参数的情形 设某总体 X 服从一个离散分布, X a1 ... ak P p1 ... pk p1 , · · · , pk 完全已知. 现从该总体抽得一个样本量为 n 的样本, 其落 在类别 a1 , · · · , ak 的观测数分别为 n1 , · · · , nk . 感兴趣的问题是检验 理论频率是否正确, 即下面假设是否正确: H0 : P (X = a1 ) = p1 , · · · , P (X = ak ) = pk . 这类问题只提零假设而不提对立假设, 相应的检验方法称为拟合优度 检验. 显然, 在零假设下, 各类别的理论频数分别为 np1 , · · · , npk , 将 理论频数和观测频数列于下表: Previous Next First Last Back Forward 2 

5 . 类别 a1 a2 ··· ak 理论频数 np1 np2 ··· npk 观测频数 n1 n2 ··· nk 由大数定律知, 在零假设成立时, ni /n 依概率收敛于 pi , 故理论 频数 npi 与观测频数 ni 接近. Pearson 提出检验统计量 ∑k (ni − npi )2 ∑ (O − E)2 T = = . i=1 npi E 可以严格地证明, 在一定的条件下, 当 H0 成立时, T 的极限分布 就是自由度为 k − 1 的 χ2 分布. 拒绝域: T > χ2α (k − 1) Previous Next First Last Back Forward 3 

6 . 下面给出一个例子来说明拟合优度检验的应用. ↑Example 有人制造一个含 6 个面的骰子, 并声称是均匀的. 现设计一个实 验来检验此命题: 连续投掷 600 次, 发现出现六面的频数分别为 97, 104, 82, 110, 93, 114. 问能否在显著性水平 0.2 下认为骰子是均匀 的? ↓Example 解: 该问题设计的总体是一个有 6 个类别的离散总体, 记出现六个面 的概率分别为 p1 , · · · , p6 , 则零假设可以表示为 H0 : pi = 1/6, i = 1, · · · , 6. 在零假设下, 理论频数都是 100, 故检验统计量 χ2 的取值为 (97−100)2 (104−100)2 (82−100)2 (110−100)2 (93−100)2 (114−100)2 100 + 100 + 100 + 100 + 100 + 100 =6.94, 跟自由度为 6 − 1 = 5 的 χ2 分布的上 0.05 分位数 χ25 (0.2) ≈ 7.29 比 较, 不能拒绝零假设, 即可在显著性水平 0.2 下认为骰子是均匀的. Previous Next First Last Back Forward 4 

7 . ↑Example 孟德尔 (Mendel) 豌豆杂交试验。纯黄和纯绿品种杂交，因为 黄色对绿色是显性的，在 Mendel 第一定律 (自由分离定律) 的假 设下，二代豌豆中应该有 75％是黄色的，25％是绿色的。在产生的 n = 8023 个二代豌豆中，有 n1 = 6022 个黄色，n2 = 2001 个绿色。 我们的问题是检验这些这批数据是否支持 Mendel 第一定律，要检验 的假设是 H0 : π1 = 0.75, π2 = 0.25 ↓Example 解: 在 Mendel 第一定律 (H0 ) 下，黄色和绿色的个数期望值为 µ1 = nπ1 = 8023∗0.75 = 6017.25, µ2 = nπ2 = 8023∗0.25 = 2005.75 则 Pearson χ2 统计量为 ∑ (O−E)2 Z= E =(6022−6017.25)2 /6017.25+(2001−2005.75)2 /2005.75=0.015 自由度 df = 1，p − value 为 0.99996. 因此可以认为这些数据服从 Mendel 第一定律。Fisher 基于 Mendel 的这些数据，发现其数据与 Previous Next First Last Back Forward 5 

8 .理论值符合的太好，p − value = 0.99996，但这么好的拟合在几千次 试验中才发生一次，因而 Fisher 断定数据可能有伪造的嫌疑。 (2) 理论总体分布含若干未知参数的情形 设某总体 X 服从一个离散 分布, X a1 ... ak P p1 ... pk pi = pi (θ1 , . . . , θr ), i = 1, . . . , k 依赖于 r 个未知参数 θ1 , . . . , θr . 此 时理论频数 npi 一般也与这些参数有关, 从而使用最大似然估计代替 这些参数以得到 pi 的最大似然估计 pˆi , 得到的统计量记为 ∑k (ni − nˆpi )2 χ2 = . i=1 nˆ pi 拟合优度检验的提出者 Karl Pearson 最初认为在零假设下, 检验统计 量的 χ2 的极限分布仍等于自由度为 k − 1 的 χ2 分布, R. A. Fisher 发现自由度应该等于 k −1 减去估计的独立参数的个数 r, 即 k −1−r. Previous Next First Last Back Forward 6 

9 . ↑Example 从某人群中随机抽取 100 个人的血液, 并测定他们在某基因位点 处的基因型. 假设该位点只有两个等位基因 A 和 a, 这 100 个基因型 中 AA, Aa 和 aa 的个数分别为 30, 40, 30, 则能否在 0.05 的水平下 认为该群体在此位点处达到 Hardy-Weinberg 平衡态? ↓Example 解: 取零假设为 H0 : Hardy-Weinberg 平衡态成立. 设人群中等位基因 A 的频率为 p, 则该人群在此位点处达到 Hardy- Weinberg 平衡态指的是在人群中 3 个基因型的频率分别为 P (AA) = p2 , P (Aa) = 2p(1 − p) 和 P (aa) = (1 − p)2 , 即零假设可等价地写成 H0 : P (AA) = p2 , P (Aa) = 2p(1 − p), P (aa) = (1 − p)2 . 在 H0 下, 3 个基因型的理论频数为 100 × pˆ2 , 100 × 2 × pˆ2 (1 − pˆ) 和 100 × (1 − pˆ)2 , 其中 pˆ 等于估计的等位基因频率 0.5, 代入 χ2 Previous Next First Last Back Forward 7 

10 .统计量表达式, 得统计量的值等于 4. 该统计量的值大于自由度为 3 − 1 − 1 = 1 (恰好一个自由参数被估计) 的 χ2 分布上 0.05 分位数 3.84, 故可在 0.05 的水平下认为未达到 Hardy-Weinberg 平衡态. 7.3.2 列联表的独立性和齐一性检验 (1) 独立性检验 下面考虑很常用的列联表. 列联表是一种按两个属性作双向分类 的表. 例如肝癌病人可以按所在医院 (属性 A) 和是否最终死亡 (属 性 B) 分类. 目的是看不同医院的疗效是否不同. 又如婴儿可按喂养 方式 (属性 A, 分两个水平: 母乳喂养与人工喂养) 和小儿牙齿发育状 况 (属性 B, 分两个水平: 正常与异常) 来分类. 这两个例子中两个属 性都只有两个水平, 相应的列联表称为 “四格表”, 一般地, 如果第一 个属性有 a 个水平, 第二个属性有 b 个水平, 称为 a × b 表 (见教材 p268) . 实际应用中, 常见的一个问题是考察两个属性是否独立. 即零 Previous Next First Last Back Forward 8 

11 .假设是 H0 : 属性 A 与属性 B 独立. 这是列联表的独立性检验问题. 假设样本量为 n, 第 (i, j) 格的频数为 nij . 记 pij = P (属性 A, B 分别处于水平i, j), (7.1) ui = P (属性 A 有水平i), (7.2) vi = P (属性 B 有水平j) (7.3) 则零假设等价于 H0 : pij = ui vj ∀i, j 将 ui 和 vj 看成参数, 则总的独立参数有 a − 1 + b − 1 = a + b − 2 个. 它们的极大似然估计为 ni· n·j u ˆi = , vˆj = . n n Previous Next First Last Back Forward 9 

12 . ∑b 正好是它们的频率 (证明参看教材) . 其中 ni· = j=1 nij , n·j = ∑a n ij . 在 H 0 下, 第 (i, j) 格的理论频数为 nˆ pij = ni· n·j /n, 因此 i=1 ∑ ∑ 在 H0 下, ai=1 bj=1 (nij − nˆ pij ) 应该较小. 故取检验统计量为 ∑a ∑ b (nij − ni· n·j /n)2 χ2 = . i=1 j=1 (ni· n·j /n) 在零假设下 χ2 的极限分布是有自由度为 k − 1 − r = ab − 1 − (a + b − 2) = (a − 1)(b − 1) 的 χ2 分布. 对于四格表, 自由度为 1. (2) 齐一性检验 跟列联表有关的另一类重要的检验是齐一性检验, 即检验某一个 属性 A 的各个水平对应的另一个属性 B 的分布全部相同, 这种检验 跟独立性检验有着本质的区别. 独立性问题中两属性都是随机的; 而 齐一性问题中属性 A 是非随机的, 这样涉及到的分布实际上是条件分 布. 虽然如此, 所采用的检验方法跟独立性检验完全一样. Previous Next First Last Back Forward 10 

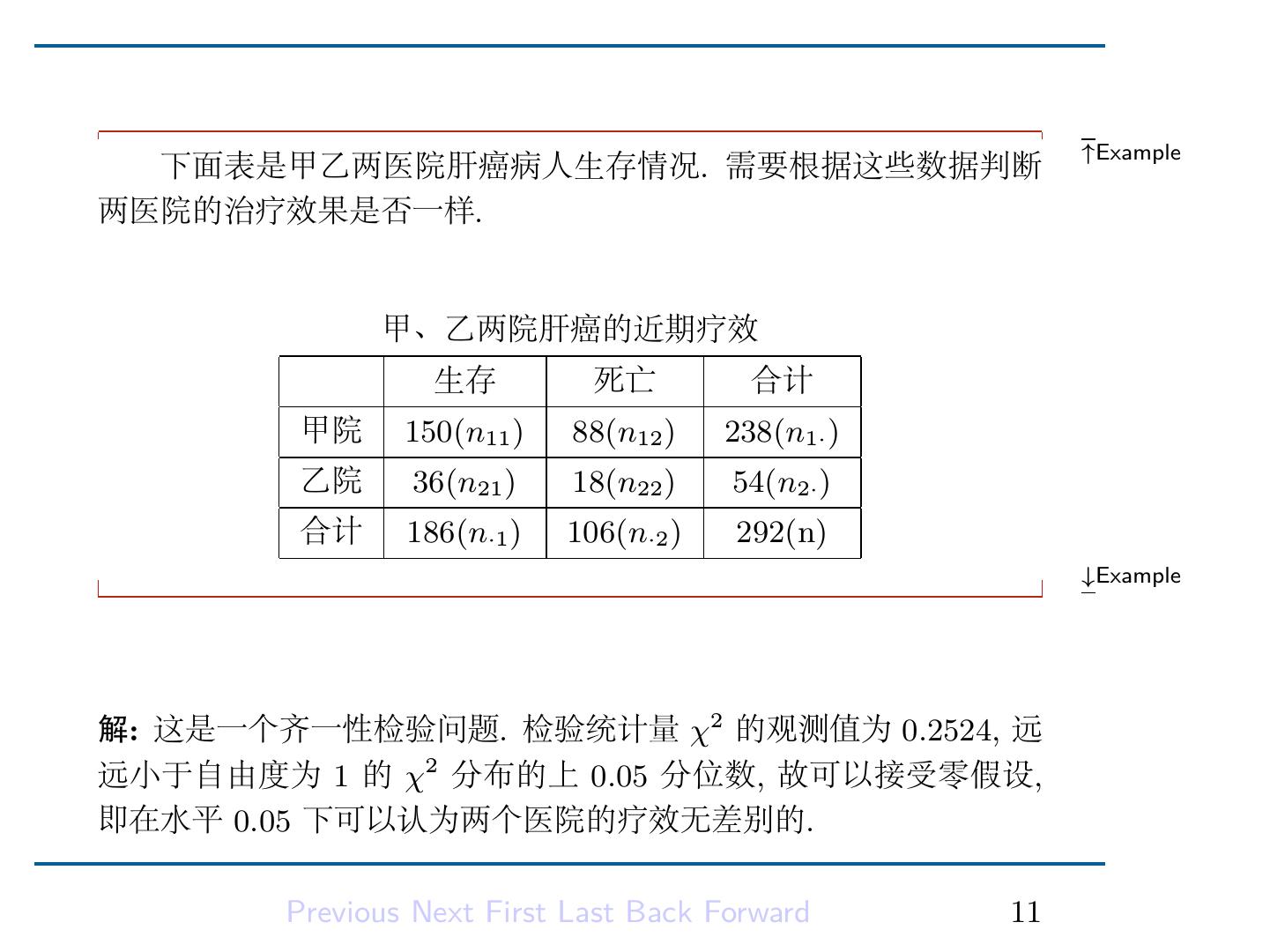
13 . ↑Example 下面表是甲乙两医院肝癌病人生存情况. 需要根据这些数据判断 两医院的治疗效果是否一样. 甲、乙两院肝癌的近期疗效 生存 死亡 合计 甲院 150(n11 ) 88(n12 ) 238(n1· ) 乙院 36(n21 ) 18(n22 ) 54(n2· ) 合计 186(n·1 ) 106(n·2 ) 292(n) ↓Example 解: 这是一个齐一性检验问题. 检验统计量 χ2 的观测值为 0.2524, 远 远小于自由度为 1 的 χ2 分布的上 0.05 分位数, 故可以接受零假设, 即在水平 0.05 下可以认为两个医院的疗效无差别的. Previous Next First Last Back Forward 11 

14 .7.3.3 连续总体情形 设 (X1 , · · · , Xn ) 是取自总体 X 的一个样本, 记 X 的分布函数 为 F (x), 需要检验的那种分布中含有 r 个总体参数 θ1 , · · · , θr . 我们 要在显著性水平 α 下检验 H0 : F (x) = F0 (x; θ1 , · · · , θr ), 其中 F0 (x; θ1 , · · · , θr ) 表示需要检验的那种分布的分布函数. 例如, 当我们要检验 H0 : X ∼ N (µ, σ 2 ) 时, r = 2, θ1 = µ, θ2 = σ 2 . ∫ x { } 1 1 F0 (x; µ, σ 2 ) = √ exp − 2 (t − µ)2 dt. −∞ 2πσ 2 2σ 上述假设可以通过适当的离散化总体分布, 采用拟合优度法来做 检验. 首先把实数轴分成 k 个子区间 (aj−1 , aj ], j = 1, · · · , k, 其中 Previous Next First Last Back Forward 12 

15 .a0 可以取 −∞, ak 可以取 ∞. 这样构造了一个离散总体, 其取值就 是这 k 个区间. 记 pj = PH0 (aj−1 < X ≤ aj ) = F0 (aj ; θ1 , · · · , θr ) − F0 (aj−1 ; θ1 , · · · , θr ), j = 1, · · · , k. 如果 H0 成立, 则概率 pj 应该与数据落在区间 (aj−1 , aj ] 的频率 fj = nj /n 接近, 其中 nj 表示相应的频数. 当 pi 的取值不含未知参 数时, 取检验统计量 ∑k (nj − npj )2 χ2 = , j=1 npj 否则取 ∑k (nj − nˆpj )2 χ2 = , j=1 nˆ pj 其中 pˆi 是将 pi 中的未知参数换成适当的估计后得到的 pi 的估计. Previous Next First Last Back Forward 13 

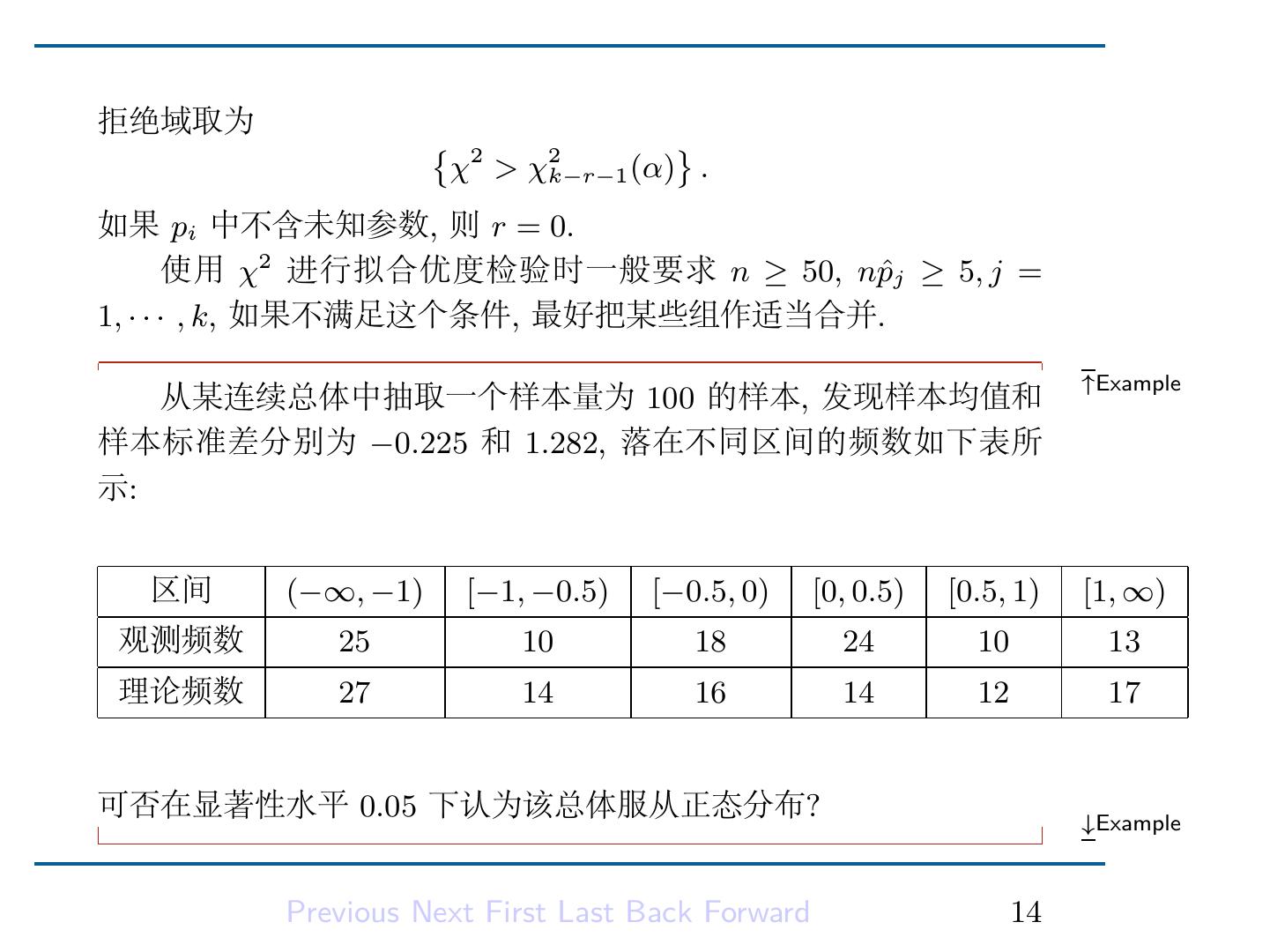
16 .拒绝域取为 { 2 } χ > χ2k−r−1 (α) . 如果 pi 中不含未知参数, 则 r = 0. 使用 χ2 进行拟合优度检验时一般要求 n ≥ 50, nˆ pj ≥ 5, j = 1, · · · , k, 如果不满足这个条件, 最好把某些组作适当合并. ↑Example 从某连续总体中抽取一个样本量为 100 的样本, 发现样本均值和 样本标准差分别为 −0.225 和 1.282, 落在不同区间的频数如下表所 示: 区间 (−∞, −1) [−1, −0.5) [−0.5, 0) [0, 0.5) [0.5, 1) [1, ∞) 观测频数 25 10 18 24 10 13 理论频数 27 14 16 14 12 17 可否在显著性水平 0.05 下认为该总体服从正态分布? ↓Example Previous Next First Last Back Forward 14 

17 .解: 设理论正态分布的均值和方差分别为 µ 和 σ 2 , 记第 i 个区间 为 (ai−1 , ai , i = 1, · · · , 6, 则样本落在第 i 个格子的理论概数为 100P (ai−1 < X ≤ ai ), 其中 X ∼ N (µ, σ 2 ). 将 µ = −0.225 和 σ 2 = 100 99 × 1.2822 = 1.622 代入得到估计的理论频数, 列于上表中. H0 : 总体服从正态分布 由此算得检验统计量 χ2 的值约为 9.25, 与自由度为 6-1-2=3 的 χ2 分布的上 0.05 分位数 χ23 (0.05) ≈ 7.81 比较可以拒绝零假设, 即可以 在显著性水平 0.05 下认为该总体不服从正态分布. Previous Next First Last Back Forward 15 

18 . P 值 若检验的拒绝域为 T (X) > τ , 对两组不同的样本 X1 和 X2 , 若它们均落在拒绝域: T (X1 ) > τ, T (X2 ) > τ 则它们否定原假设的程度一样吗? 如何区分这个差异? P 值 = P (在H0 �,得到如检验统计量T (X)的值T (x)这么大或者更极端) 从而可以通过 P 值来比较样本的支持程度. 对不同的水平 α 检验方法, 可以通过比较它们的功效 (二型错误) 来评比优劣. Previous Next First Last Back Forward 16