1.7-2: 假设检验 张伟平 

2.第七讲: 假设检验 7.2 一样本和两样本总体参数检验 . . . . . . . . . 1 7.2.1 一样本正态总体参数检验 . . . . . . . 1 7.2.2 两样本正态总体的情形 . . . . . . . . . 13 7.2.3 成对数据 . . . . . . . . . . . . . . . . 18 7.2.4 0-1 分布中未知参数 p 的假设检验 . . 19 7.2.5 置信区间和假设检验之间的关系 . . . . 21 Previous Next First Last Back Forward 1 

3. 7.2 一样本和两样本总体参数检验 本节介绍最基本的假设检验问题: 一样本和两样本正态总体的有 关均值和方差的检验, 简单的大样本检验 (0-1 分布参数的假设检验). 7.2.1 一样本正态总体参数检验 一般地, 设总体 X ∼ N (µ, σ 2 ), −∞ < µ < ∞, σ 2 > 0; X1 , · · · , Xn 是取自总体 X 的一个样本. 取显著性水平为 α. 则可能考虑的参数有 均值 µ 和方差 σ 2 : (1) 方差已知时均值的检验 先考虑双侧假设, 即要检验 H0 : µ = µ0 ↔ H1 : µ ̸= µ0 . Previous Next First Last Back Forward 1 

4. ¯ 取 “标准化” 后的检验统计量 由于 µ 的极大似然估计为 X, √ X¯ − µ0 Z = Z(X1 , · · · , Xn ) = n σ 注意到当 H0 成立时, U ∼ N (0, 1), |Z| 应该较小, 反之当 |U | 的观 测值 z(x1 , · · · , xn ) 较大时, 不利于零假设 H0 应该拒绝之. 所以选拒 绝域形如 {|Z| > τ }. 要求显著性水平为 α, 即 PH0 (|Z| > τ ) = α, 解得 τ = zα/2 . 于是检验的拒绝域为 {|Z| > uα/2 }. 即当观测值 (x1 , · · · , xn ) 满足不等式 √ |¯ x − µ0 | n > uα/2 σ Previous Next First Last Back Forward 2 

5.时拒绝 H0 . 类似地, 检验右侧假设 H0 : µ = µ0 ↔ H1 : µ > µ0 或者 H0 : µ ≤ µ0 ↔ H1 : µ > µ0 仍然用统计量 Z, 由于 Z 大时不利于 H0 , 取拒绝域为 {Z > uα } . 而检验另一个左侧假设 H0 : µ = µ0 ↔ H1 : µ < µ0 或者 H0 : µ ≤ µ0 ↔ H1 : µ < µ0 的拒绝域为 {Z < −uα } . 虽然我们取的临界值只考虑使检验在 µ = µ0 处的犯 I 类错误的概率 为 α, 从检验的拒绝域的形状上可直接看出来在零假设下 µ ≤ µ0 (或 µ ≥ µ0 ) 时犯第 I 类错误的概率恒小于或等于 α. Previous Next First Last Back Forward 3 

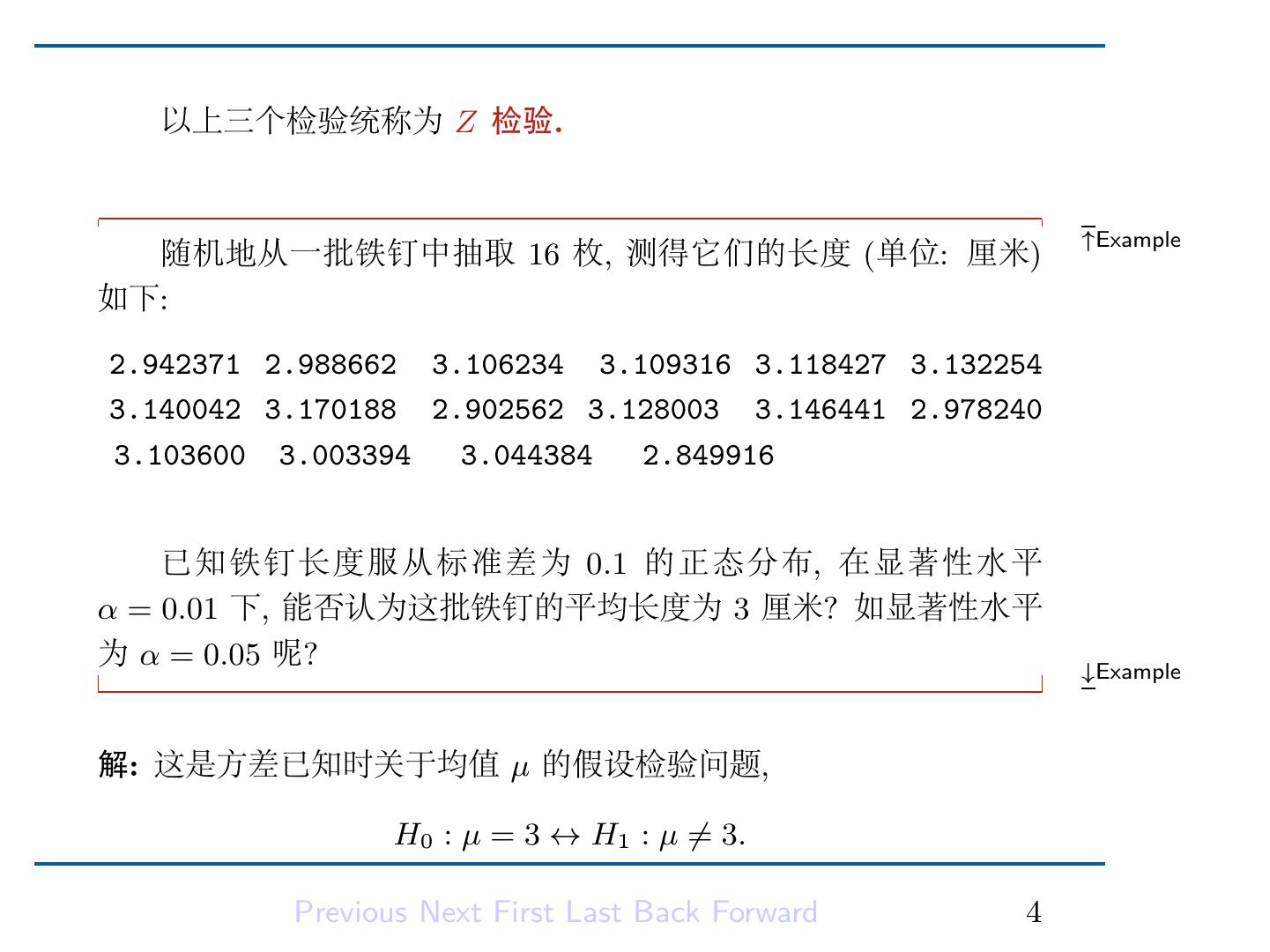
6. 以上三个检验统称为 Z 检验. ↑Example 随机地从一批铁钉中抽取 16 枚, 测得它们的长度 (单位: 厘米) 如下: 2.942371 2.988662 3.106234 3.109316 3.118427 3.132254 3.140042 3.170188 2.902562 3.128003 3.146441 2.978240 3.103600 3.003394 3.044384 2.849916 已知铁钉长度服从标准差为 0.1 的正态分布, 在显著性水平 α = 0.01 下, 能否认为这批铁钉的平均长度为 3 厘米? 如显著性水平 为 α = 0.05 呢? ↓Example 解: 这是方差已知时关于均值 µ 的假设检验问题, H0 : µ = 3 ↔ H1 : µ ̸= 3. Previous Next First Last Back Forward 4 

7. √ ¯ 取检验统计量为 Z = n(X − 3)/0.1, 检验的拒绝域为 |Z| > uα/2 . 由样本算得检验统计量的值为 z ≈ 2.16, 如显著性水平为 0.01, 则临 界值为 u0.005 ≈ 2.58, 跟检验统计量的值比较发现不能拒绝零假设, 即不能推翻铁钉平均长度为 3 厘米的假设; 而如果显著性水平为 0.05 时, 临界值为 u0.025 = 1.96, 此时可以拒绝零假设, 认为铁钉平均长度 不等于 3 厘米. 这个例子说明结论可能跟显著性水平的选择有关: 显 著性水平越小, 零假设被保护得越好从而更不容易被拒绝. ↑Example 对正态总体 N (µ, σ 2 )(其中 σ 2 已知) 下的假设检验问题 H0 : µ ≥ µ0 ↔ H1 : µ < µ0 ，如果我们还要求“犯第二类错误的概率要小于指 定的 β > 0”该怎么办？ ↓Example 解：根据功效函数和两类错误的定义，知道等价的要求 βϕ (µ) ≥ 1 − β, µ < µ0 (7.1) 但是，当 µ < µ0 但 µ 接近 µ0 时，βϕ (µ) ≈ α，而因为 α, β 一般都 很小，因此一般有 α < 1 − β，这就看出要求 (7.1) 无法达到。我们 Previous Next First Last Back Forward 5 

8.只能放松一些，要求对某个指定的 µ1 < µ0 ，有 βϕ (µ) ≥ 1 − β, µ < µ1 (7.2) 因为 βϕ (µ) 为 µ 的减函数，因此等价于要求 βϕ (µ1 ) ≥ 1 − β 此即 (√ ) n(µ0 − µ) Φ − uα ≥ 1 − β σ 等价的得到 n ≥ σ 2 (uα + uβ )2 /(µ0 − µ)2 也即要满足题目中的要求，样本大小至少要达到上式右边那么大。 Previous Next First Last Back Forward 6 

9.(2) 方差未知时均值的检验 考虑检验 H0 : µ = µ0 ↔ µ ̸= µ0 , 由于方差未知, 可以在将 X¯ 标准化的过程中用样本方差 S 2 代替总体 2 方差 σ , 得检验统计量 √ X¯ − µ0 T = n . S 由于在 H0 下, T ∼ tn−1 , 于是拒绝域取成 {|T | > tn−1 (α/2)} . 此检验称为t 检验. 类似地可以得到另外两个单侧假设的检验拒绝域, 见表 7.2.1 中. Previous Next First Last Back Forward 7 

10. ↑Example (例7.2.1续) 设方差未知, 则在水平 0.01 和 0.05 下能否认为铁钉 平均长度为 3 厘米? ↓Example 解: 这是方差未知时关于均值 µ 的假设检验问题, H0 : µ = 3 ↔ H1 : µ ̸= 3 √ ¯ 取检验统计量为 T = n(X − 3)/S, 检验的拒绝域为 |T | > tn−1 (α/2). 由样本算得检验统计量的值约为 2.21, 与显著性水平 0.01 对应临界 值 t15 (0.005) ≈ 2.95 比较, 不能拒绝零假设, 而与显著性水平 0.05 对 应临界值 t15 (0.025) ≈ 2.13 比较, 可以拒绝零假设, 即在显著性水平 0.01 下不能拒绝铁钉平均长度为 3 厘米的假定, 但在显著性水平 0.05 下可以认为铁钉平均长度不等于 3 厘米, 此结论与方差已知情形一致. Previous Next First Last Back Forward 8 

11.(3) 方差的检验 考虑假设检验问题 H0 : σ 2 = σ02 ↔ H1 : σ 2 ̸= σ02 . 对均值已知的情形, 由 σ 2 的极大似然估计 1∑ n ˆ2 = σ (Xi − µ)2 n i=1 可以构造检验统计量 1 ∑ n nˆσ2 χ2 = 2 (Xi − µ)2 = 2 . σ0 i=1 σ0 σ 2 nˆ σ2 在 H0 下, χ2 ∼ χ2n , χ2 的平均值为 n, 而在 H1 下, χ2 = σ02 σ2 的 σ2 均值为 2n σ0 ̸= n, 因此当 χ 的值过于偏离 n 时应该拒绝 H0 , 于是拒 2 绝域取成 { } χ2 < χ2n (1 − α/2) 或者 χ2 > χ2n (α/2) . Previous Next First Last Back Forward 9 

12. 对均值未知的情形, 构造检验统计量 (n − 1)S 2 χ2 = , σ02 其中 S 2 为样本方差. 在 H0 下, χ2 ∼ χ2n−1 , 拒绝域取成 { } χ2 < χ2n−1 (1 − α/2) 或者 χ2 > χ2n−1 (α/2) . 对于单侧假设, 可以类似得到检验的拒绝域, 参看下表 7.2.1. 上述检验称为 χ2 检验. Previous Next First Last Back Forward 10 

13.Previous Next First Last Back Forward 11 

14. ↑Example (例7.2.1续) 在水平 0.1 下能否认为铁钉的标准差大于 0.1 厘米? ↓Example 解: 这是均值未知时关于方差 σ 2 的假设检验问题, H0 : σ 2 ≤ 0.12 ↔ H1 : σ 2 > 0.12 . 2 取检验统计量为 χ2 = (n−1)S 0.12 , 检验的拒绝域为 {χ2 > χ2n−1 (α)}. 由 样本算得检验统计量的值 χ2 ≈ 14.32, 与显著性水平 0.2 对应临界值 χ215 (0.1) ≈ 22.31 比较, 不能拒绝零假设, 即在显著性水平 0.1 下可以 认为铁钉的标准差小于 0.1. Previous Next First Last Back Forward 12 

15.7.2.2 两样本正态总体的情形 设 总 体 X ∼ N (µ1 , σ12 ), Y ∼ N (µ2 , σ22 ), −∞ < µ1 , µ2 < ∞, σ12 , σ22 > 0; X1 , · · · , Xn 是从总体 X 中抽取的一个样本, Y1 , · · · , Yn 是从总体 Y 中抽取的一个样本. 设来自不同总体的样本相互独立. 下 面设考虑有关均值差 µ1 − µ2 和方差比 σ12 /σ22 的检验. 取显著性水平 为 α. ↑Example 甲乙两个农业试验区种植玉米, 除了甲区施磷肥外, 其他试验条 件都相同, 把两个试验区分别均分成 10 个和 9 个小区统计产量 (单 位: 千克) , 得数据如下 甲区 62 57 65 60 63 58 57 60 60 58 乙区 50 59 56 57 58 57 56 55 57 假定甲乙两区中每小块的玉米产量分别服从 N (µ1 , σ 2 ), N (µ2 , σ 2 ), 其中 µ1 , µ2 , σ 2 未知. 试问在显著性水平 α = 0.1 下磷肥对玉米的产 量是否有效? ↓Example Previous Next First Last Back Forward 13 

16.解: 磷肥对玉米产量有效果等价于 µ1 > µ2 , 故将其设为对立假设, 假 设检验问题是 H0 : µ1 ≤ µ2 = 0 ↔ H1 : µ1 > µ2 . 构造基于 µ1 − µ2 的极大似然估计 X ¯ − Y¯ 的检验统计量 ¯ − Y¯ X T = √ . 1 1 Sw m + n 当 H0 成立时, T ∼ tm+n−2 , 于是拒绝域为 {T > tm+n−2 (α))} . 由所得数据算得检验统计量 T 的观测值为 ¯ − y¯ x t= √ = 3.23. 1 1 sw m + n Previous Next First Last Back Forward 14 

17.由 α = 0.1 得临界值为 tm+n−2 (α/2) = t17 (0.1) ≈ 1.33 < 3.23, 因此 拒绝 H0 , 即可以在显著性水平 0.1 下认为磷肥对玉米的产量有显著 性影响. ↑Example 在例7.2.2中假定了两个正态总体的方差是相等的, 即 σ12 = σ22 = 2 σ . 现在我们根据样本来检验这个方差齐性的假设, 即要检验 σ12 σ2 H0 : 2 = 1 ↔ H1 : 12 ̸= 1. σ2 σ2 ↓Example 解: 因为 σ12 和 σ22 的极大似然估计分别是 1 ∑ 1∑ m n ˆ12 = σ (Xi − X) ¯ 2, σ ˆ22 = (Yi − Y¯ )2 . m i=1 n i=1 Previous Next First Last Back Forward 15 

18.在 θ = σ12 /σ22 的极大似然估计 θˆ = σ ˆ12 /ˆ σ22 的基础上可以构造检验统 计量 S2 (m − 1)ˆ σ12 /m F = 12 = . S2 (n − 1)ˆ σ22 /n 注意到 F 中的分子和分母分别是 X 和 Y 的样本方差. 当零假设成 立时, F ∼ Fm−1,n−1 . 于是拒绝域为 {F < Fm−1,n−1 (α/2) 或 F > Fm−1,n−1 (1 − α/2)}. 由数据算得检验统计量 F 的观测值 f = 1.19, 如果取显著性水平 α = 0.2, 那么临界值为 F9,8 (0.1) = 2.44, F9,8 (0.9) = 1/F8,9 (0.1) = 0.41 (如果 X ∼ Fm,n , 则 1/X ∼ Fn,m ). 易见 0.41 < 1.19 < 2.44, 因此不能拒绝 H0 , 即在显著性水平 0.2 下可以认为上例中所作的方 差齐性假定是合理的. Previous Next First Last Back Forward 16 

19.Previous Next First Last Back Forward 17 

20.7.2.3 成对数据 在上述两样本正态总体的假设检验中, 要求两个样本是独立的, 但是没有要求样本量相等. 有一类数据叫做成对数据 {(X1 , Y1 ), · · · , (Xn , Yn )} • 数据对之间通常可以认为是独立的 • 数据对内两个观测通常不独立 比如一个病人在用药前后测得的指标分别为 X 和 Y 当数据是连续数据时候, 通常对数据对内取差, 构造一个新的总 体 Z = Y − X 及样本 Z1 = X1 − Y1 , · · · , Zn = Xn − Yn , 通常假设 Z 服从正态, 则相应的假设检验转为一样本正态检验问题! Previous Next First Last Back Forward 18 

21.7.2.4 0-1 分布中未知参数 p 的假设检验 产品验收时, 需要检验不合格率是否小于某给定的一个数. 设 (X1 , · · · , Xn ) 是取自总体 X 的一个样本, 该总体服从 0-1 分 布, 取 1 的概率为 p. 常见的假设有三种: (1) H0 : p = p0 ↔ H1 : p ̸= p0 ; (2) H0 : p = p0 ↔ H1 : p > p0 或 H0 : p ≤ p0 ↔ H1 : p > p0 ; (3) H0 : p = p0 ↔ H1 : p < p0 或 H0 : p ≥ p0 ↔ H1 : p < p0 . 假定样本量 n 较大, 取显著性水平为 α. 由于 p 的极大似然估计 ¯ 取 “标准化” 过的检验统计量 为 X, √ X¯ − p0 T = n√ , p0 (1 − p0 ) 其中 p0 和 p0 (1 − p0 )/n 分别为 X ¯ 在零假设 p = p0 下的期望和方 差, 从而当 H0 成立时, 由中心极限定理近似地有 T ∼ N (0, 1). 于是 上述三种检验的拒绝域分别为 {|T | > uα/2 , {T > uα } 和 {T < −uα } Previous Next First Last Back Forward 19 

22. ↑Example 某厂产品不合格率通常为 0.5. 厂方希望知道原料产地的改变是 否对产品的质量发生显著的影响. 现在随机地从原料产地改变后的产 品中抽取了 80 个样品进行检验, 发现有 5 个是不合格品. 试问, 在显 著性水平 0.1 下, 厂方由此可以得出什么结论? ↓Example 解: 总体 X ∼ B(1, p), 其中 p 未知. 在显著性水平 α = 0.1 下, 产品 质量无变化等价于 p = 0.05, 故我们要检验 H0 : p = 0.05 ↔ H1 : p ̸= 0.05. 由于 x ¯ = 5/80 = 0.0625, 因此检验统计量 T 的观测值 √ ¯ − p0 x t= n√ = 0.513. p0 (1 − p0 ) 由 α = 0.10 得临界值 u0.05 = 1.645. 易见, |t| < 1.645, 因此不能拒 Previous Next First Last Back Forward 20 

23.绝 H0 , 即在近似显著性水平 0.10 下可以认为原料产地的改变对该厂 产品的质量没有发生显著的影响. 7.2.5 置信区间和假设检验之间的关系 置信区间和假设检验之间有着明显的联系。我们首先考虑置信区 间和双边检验之间的关系。设 X1 , · · · , Xn 为从总体 F (x; θ) 中抽取 ¯ 即 的样本，参数 θ 的 1 − α 置信区间为 [θ, θ], ¯ P (θ ≤ θ ≤ θ) 1−α 而对假设 H0 : θ = θ0 ↔ H1 : θ ̸= θ0 ，在原假设之下，有 ¯ P (θ ≤ θ0 ≤ θ) 1−α 等价于 ¯ + P (θ0 < θ) ≤ α P (θ0 > θ) Previous Next First Last Back Forward 21 

24.按显著性检验的定义，即得其检验为 ϕ : 当 θ ≤ θ0 ≤ θ¯ 时，接受H0 , 不然就拒绝 反过来讲, 如果假设 H0 : θ = θ0 ↔ H1 : θ ̸= θ0 检验的接受域有 形式 ¯ 1 , · · · , xn ) θ(x1 , · · · , xn ) ≤ θ0 ≤ θ(x 即有 ¯ P (θ ≤ θ0 ≤ θ) 1−α 由 θ0 的任意性，知对任意的 θ，有 ¯ P (θ ≤ θ ≤ θ) 1−α 即：为求出参数 θ 的 1 − α 置信区间，我们可以先找出 θ 的双边检 验 H0 : θ = θ0 ↔ H1 : θ ̸= θ0 的检验函数，则其接受域就是参数 θ 的 1 − α 置信区间。反过来，为求假设 H0 : θ = θ0 ↔ H1 : θ ̸= θ0 Previous Next First Last Back Forward 22 

25.的检验，我们可以先求出参数 θ 的 1 − α 置信区间，则就是该假设的 接受域。 类 似 地， 置 信 水 平 为 1 − α 的 单 侧 置 信 区 间 (θ, ∞) (或 者 ¯ 与显著性水平为 α 的右 (或者左) 边检验问题 H0 : θ ≤ (−∞, θ)) θ0 ↔ H1 : θ > θ0 (或者 H0 : θ ≥ θ0 ↔ H1 : θ < θ0 )，也有类似的对 应关系。 Previous Next First Last Back Forward 23