- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
设计过程与ALU设计
展开查看详情
1 . ECE4680 Computer Organization & Architecture The Design Process & ALU Design ECE4680 ALU design.1 2002-2-20 The Design Process "To Design Is To Represent" Design activity yields description/representation of an object -- Traditional craftsman does not distinguish between the concept- ualization and the artifact -- Separation comes about because of complexity -- The concept is captured in one or more representation languages -- This process IS design Design Begins With Requirements -- Functional Capabilities: what it will do -- Performance Characteristics: Speed, Power, Area, Cost, . . . ECE4680 ALU design.2 2002-2-20
2 . Design Process (cont.) Design Finishes As Assembly CPU -- Design understood in terms of Datapath Control components and how they have been assembled ALU Regs Shifter -- Top Down decomposition of complex functions (behaviors) into more primitive functions Nand Gate -- bottom-up composition of primitive building blocks into more complex assemblies Design is a "creative process," not a simple method ECE4680 ALU design.3 2002-2-20 Design Refinement Informal System Requirement Initial Specification Intermediate Specification refinement increasing level of detail Final Architectural Description Intermediate Specification of Implementation Final Internal Specification Physical Implementation ECE4680 ALU design.4 2002-2-20
3 . Design as Search Problem A Strategy 1 Strategy 2 SubProb 1 SubProb 2 SubProb 3 BB1 BB2 BB3 BBn : Basic Blocks Design involves educated guesses and verification -- Given the goals, how should these be prioritized? -- Given alternative design pieces, which should be selected? -- Given design space of components & assemblies, which part will yield the best solution? Feasible (good) choices vs. Optimal choices ECE4680 ALU design.5 2002-2-20 Design as Representation (example) (1) Functional Specification "VHDL Behavior" -A, B; 1 bit carry input- Inputs: 2 x 16 bit operands- -Cin. -S; 1 bit carry output- Outputs: 1 x 16 bit result- -Cout. Operations: PASS, ADD (A plus B plus Cin), SUB (A minus B minus Cin), AND, XOR, OR, COMPARE (equality) Performance: left unspecified for now! (2) Block Diagram "VHDL Entity" Understand the data and control flows 16 16 A B 3 M mode/function ALU Cout Cin S 16 ECE4680 ALU design.6 2002-2-20
4 . Elements of the Design Process °Divide and Conquer (e.g. ALU) • Formulate a solution in terms of simpler components. • Design each of the components (subproblems) °Generate and Test (e.g. ALU) • Given a collection of building blocks, look for ways of putting them together that meets requirement °Successive Refinement (e.g. carry lookahead) • Solve "most" of the problem (i.e., ignore some constraints or special cases), examine and correct shortcomings. °Formulate High-Level Alternatives (e.g. carry select) • Articulate many strategies to "keep in mind" while pursuing any one approach. °Work on the Things you Know How to Do • The unknown will become “obvious” as you make progress. ECE4680 ALU design.7 2002-2-20 Summary of the Design Process Hierarchical Design to manage complexity Top Down vs. Bottom Up vs. Successive Refinement Importance of Design Representations: Block Diagrams Decomposition into Bit Slices top bottom down up Truth Tables, K-Maps mux design Circuit Diagrams meets at TT Other Descriptions: state diagrams, timing diagrams, reg xfer, . . . Optimization Criteria: Power Gate Count Area Logic Levels Delay Fan-in/Fan-out Cost [Package Count] Pin Out Design time ECE4680 ALU design.8 2002-2-20
5 . Introduction to Binary Numbers Consider a 4-bit binary number Decimal Binary Decimal Binary 0 0000 4 0100 1 0001 5 0101 2 0010 6 0110 3 0011 7 0111 Examples: 3+2=5 3+3=6 1 1 1 0 0 1 1 0 0 1 1 + 0 0 1 0 + 0 0 1 1 0 1 0 1 0 1 1 0 Problems: how to represent signed number? How to do subtraction? ECE4680 ALU design.9 2002-2-20 Sign and Magnitude Representation Decimal Binary Decimal Binary 0 0000 -0 1000 1 0001 -1 1001 2 0010 -2 1010 3 0011 -3 1011 4 0100 -4 1100 5 0101 -5 1101 6 0110 -6 1110 7 0111 -7 1111 Easy for human to understand, but 0 has two representation: a problem for programmer. Need different ways to do addition and subtraction. Extra step to set sign for the result: a problem for hardware. Especially when a<b, how to do a-b ? ECE4680 ALU design.10 2002-2-20
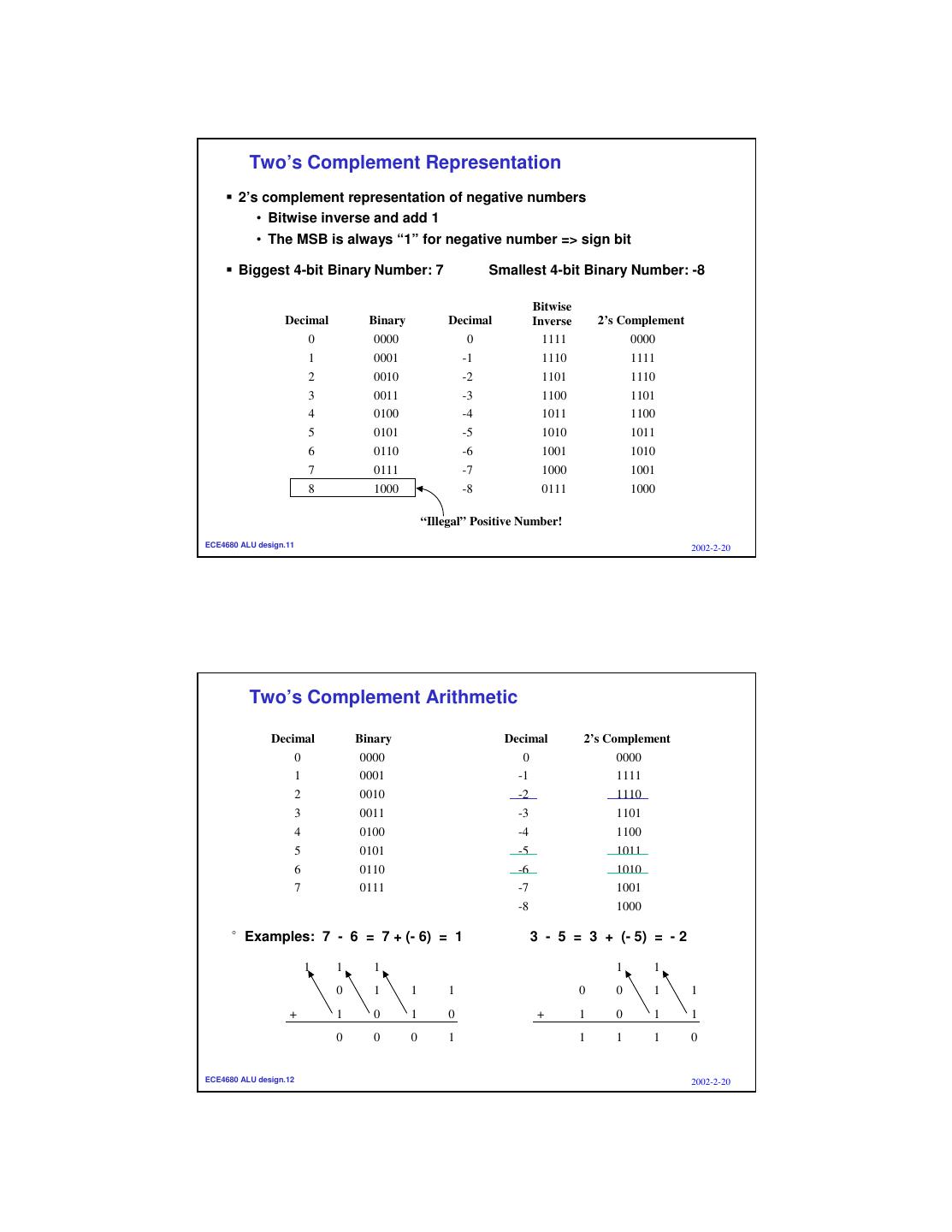
6 . Two’s Complement Representation 2’s complement representation of negative numbers • Bitwise inverse and add 1 • The MSB is always “1” for negative number => sign bit Biggest 4-bit Binary Number: 7 Smallest 4-bit Binary Number: -8 Bitwise Decimal Binary Decimal Inverse 2’s Complement 0 0000 0 1111 0000 1 0001 -1 1110 1111 2 0010 -2 1101 1110 3 0011 -3 1100 1101 4 0100 -4 1011 1100 5 0101 -5 1010 1011 6 0110 -6 1001 1010 7 0111 -7 1000 1001 8 1000 -8 0111 1000 “Illegal” Positive Number! ECE4680 ALU design.11 2002-2-20 Two’s Complement Arithmetic Decimal Binary Decimal 2’s Complement 0 0000 0 0000 1 0001 -1 1111 2 0010 -2 1110 3 0011 -3 1101 4 0100 -4 1100 5 0101 -5 1011 6 0110 -6 1010 7 0111 -7 1001 -8 1000 °Examples: 7 - 6 = 7 + (- 6) = 1 3 - 5 = 3 + (- 5) = - 2 1 1 1 1 1 0 1 1 1 0 0 1 1 + 1 0 1 0 + 1 0 1 1 0 0 0 1 1 1 1 0 ECE4680 ALU design.12 2002-2-20
7 . Two’s Complement Properties Decimal Binary Decimal 2’s Complement From 3 bits to 4 bits 0 0000 0 0000 1 0001 -1 1111 2 0010 -2 1110 3 0011 -3 1101 4 0100 -4 1100 5 0101 -5 1011 6 0110 -6 1010 7 0111 -7 1001 -8 1000 Treat subtraction the same way as for addition. Negate a number invert the number + add 1. (Page 216) Sign extension: when word is prolonged, fill sign bit into the new bits. See above example. ECE4680 ALU design.13 2002-2-20 Functional Specification of the ALU ALUop 3 A N Zero ALU Result N Overflow B N CarryOut °ALU Control Lines (ALUop) Function • 000 And • 001 Or • 010 Add • 110 Subtract • 111 Set-on-less-than ECE4680 ALU design.14 2002-2-20
8 . A One Bit ALU °This 1-bit ALU will perform AND, OR, and ADD CarryIn A and or Mux Result 1-bit add Full B Adder CarryOut ECE4680 ALU design.15 2002-2-20 A One-bit Full Adder CarryIn A 1-bit °This is also called a (3, 2) adder C Full B Adder °Half Adder: No CarryIn nor CarryOut °Truth Table: CarryOut Inputs Outputs A B CarryIn CarryOut Sum Comments 0 0 0 0 0 0 + 0 + 0 = 00 0 0 1 0 1 0 + 0 + 1 = 01 0 1 0 0 1 0 + 1 + 0 = 01 0 1 1 1 0 0 + 1 + 1 = 10 1 0 0 0 1 1 + 0 + 0 = 01 1 0 1 1 0 1 + 0 + 1 = 10 1 1 0 1 0 1 + 1 + 0 = 10 1 1 1 1 1 1 + 1 + 1 = 11 ECE4680 ALU design.16 2002-2-20
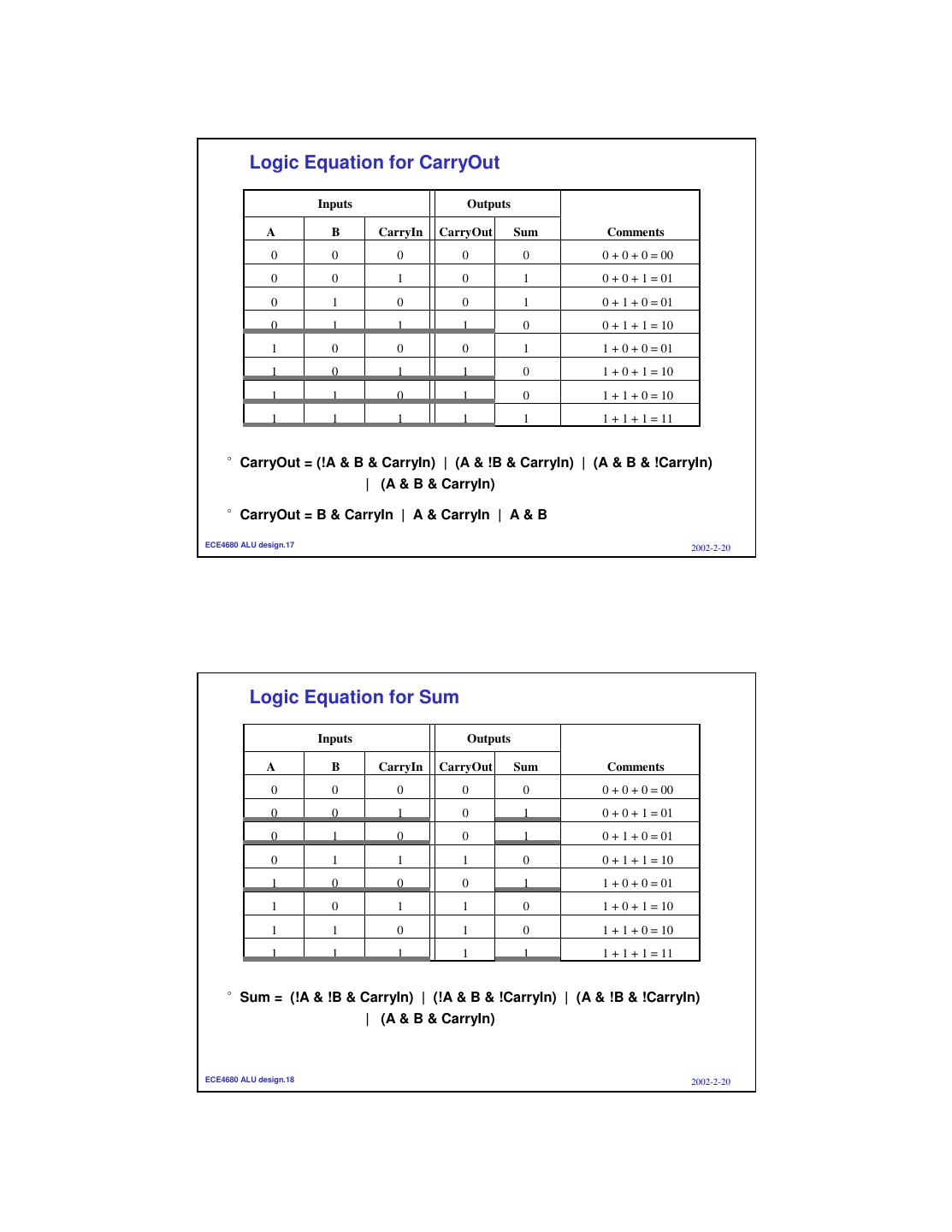
9 . Logic Equation for CarryOut Inputs Outputs A B CarryIn CarryOut Sum Comments 0 0 0 0 0 0 + 0 + 0 = 00 0 0 1 0 1 0 + 0 + 1 = 01 0 1 0 0 1 0 + 1 + 0 = 01 0 1 1 1 0 0 + 1 + 1 = 10 1 0 0 0 1 1 + 0 + 0 = 01 1 0 1 1 0 1 + 0 + 1 = 10 1 1 0 1 0 1 + 1 + 0 = 10 1 1 1 1 1 1 + 1 + 1 = 11 °CarryOut = (!A & B & CarryIn) | (A & !B & CarryIn) | (A & B & !CarryIn) | (A & B & CarryIn) °CarryOut = B & CarryIn | A & CarryIn | A & B ECE4680 ALU design.17 2002-2-20 Logic Equation for Sum Inputs Outputs A B CarryIn CarryOut Sum Comments 0 0 0 0 0 0 + 0 + 0 = 00 0 0 1 0 1 0 + 0 + 1 = 01 0 1 0 0 1 0 + 1 + 0 = 01 0 1 1 1 0 0 + 1 + 1 = 10 1 0 0 0 1 1 + 0 + 0 = 01 1 0 1 1 0 1 + 0 + 1 = 10 1 1 0 1 0 1 + 1 + 0 = 10 1 1 1 1 1 1 + 1 + 1 = 11 °Sum = (!A & !B & CarryIn) | (!A & B & !CarryIn) | (A & !B & !CarryIn) | (A & B & CarryIn) ECE4680 ALU design.18 2002-2-20
10 . Logic Equation for Sum (continue) °Sum = (!A & !B & CarryIn) | (!A & B & !CarryIn) | (A & !B & !CarryIn) | (A & B & CarryIn) °Sum = A XOR B XOR CarryIn °Truth Table for XOR: X Y X XOR Y 0 0 0 0 1 1 1 0 1 1 1 0 ECE4680 ALU design.19 2002-2-20 Logic Diagrams for CarryOut and Sum °CarryOut = B & CarryIn | A & CarryIn | A & B CarryIn A B CarryOut °Sum = A XOR B XOR CarryIn CarryIn A B Sum ECE4680 ALU design.20 2002-2-20
11 . A 4-bit ALU ° 1-bit ALU 4-bit ALU CarryIn0 CarryIn A0 1-bit A Result0 B0 ALU CarryIn1 CarryOut0 A1 1-bit Result1 Result B1 ALU Mux CarryIn2 CarryOut1 A2 1-bit Result2 B2 ALU 1-bit CarryIn3 CarryOut2 Full A3 B 1-bit Result3 Adder B3 ALU CarryOut CarryOut3 ECE4680 ALU design.21 2002-2-20 How About Subtraction? °Keep in mind the followings: • (A - B) is the that as: A + (-B) • 2’s Complement: Take the inverse of every bit and add 1 °Bit-wise inverse of B is !B: • A + !B + 1 = A + (!B + 1) = A + (-B) = A - B Subtract A CarryIn 4 Zero “ALU” Result Sel 4 2x1 Mux B 0 4 1 4 4 !B CarryOut ECE4680 ALU design.22 2002-2-20
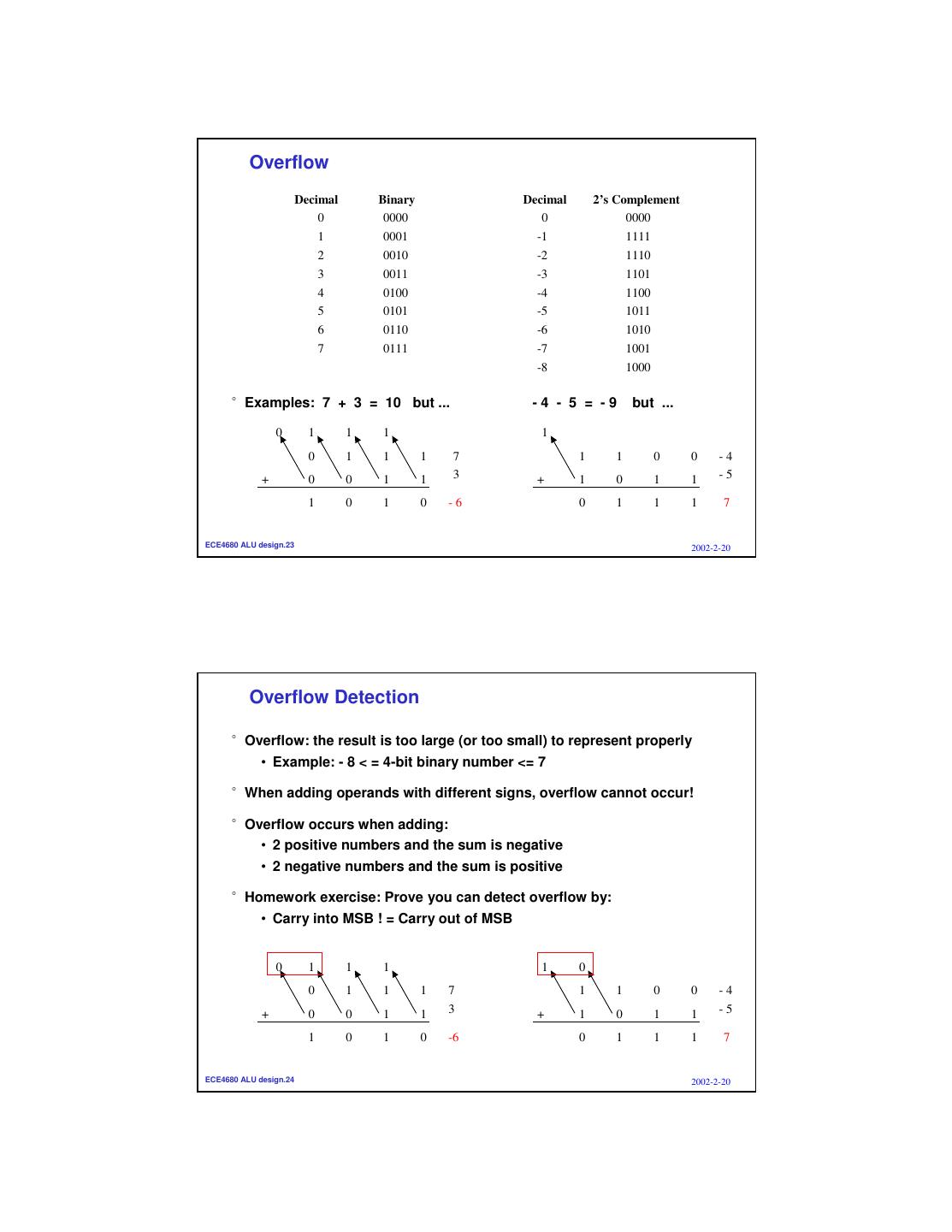
12 . Overflow Decimal Binary Decimal 2’s Complement 0 0000 0 0000 1 0001 -1 1111 2 0010 -2 1110 3 0011 -3 1101 4 0100 -4 1100 5 0101 -5 1011 6 0110 -6 1010 7 0111 -7 1001 -8 1000 °Examples: 7 + 3 = 10 but ... -4 - 5 = -9 but ... 0 1 1 1 1 0 1 1 1 7 1 1 0 0 -4 + 0 0 1 1 3 + 1 0 1 1 -5 1 0 1 0 -6 0 1 1 1 7 ECE4680 ALU design.23 2002-2-20 Overflow Detection °Overflow: the result is too large (or too small) to represent properly • Example: - 8 < = 4-bit binary number <= 7 °When adding operands with different signs, overflow cannot occur! °Overflow occurs when adding: • 2 positive numbers and the sum is negative • 2 negative numbers and the sum is positive °Homework exercise: Prove you can detect overflow by: • Carry into MSB ! = Carry out of MSB 0 1 1 1 1 0 0 1 1 1 7 1 1 0 0 -4 + 0 0 1 1 3 + 1 0 1 1 -5 1 0 1 0 -6 0 1 1 1 7 ECE4680 ALU design.24 2002-2-20
13 . Overflow Detection Logic °Carry into MSB ! = Carry out of MSB • For a N-bit ALU: Overflow = CarryIn[N - 1] XOR CarryOut[N - 1] CarryIn0 A0 1-bit Result0 X Y X XOR Y B0 ALU 0 0 0 CarryIn1 CarryOut0 A1 0 1 1 1-bit Result1 ALU 1 0 1 B1 1 1 0 CarryIn2 CarryOut1 A2 1-bit Result2 B2 ALU CarryIn3 A3 Overflow 1-bit Result3 B3 ALU CarryOut3 ECE4680 ALU design.25 2002-2-20 Zero Detection Logic °Zero Detection Logic is just a one BIG NOR gate • Any non-zero input to the NOR gate will cause its output to be zero CarryIn0 A0 1-bit Result0 B0 ALU CarryIn1 CarryOut0 A1 1-bit Result1 B1 ALU Zero CarryIn2 CarryOut1 A2 1-bit Result2 B2 ALU CarryIn3 CarryOut2 A3 1-bit Result3 B3 ALU CarryOut3 ECE4680 ALU design.26 2002-2-20
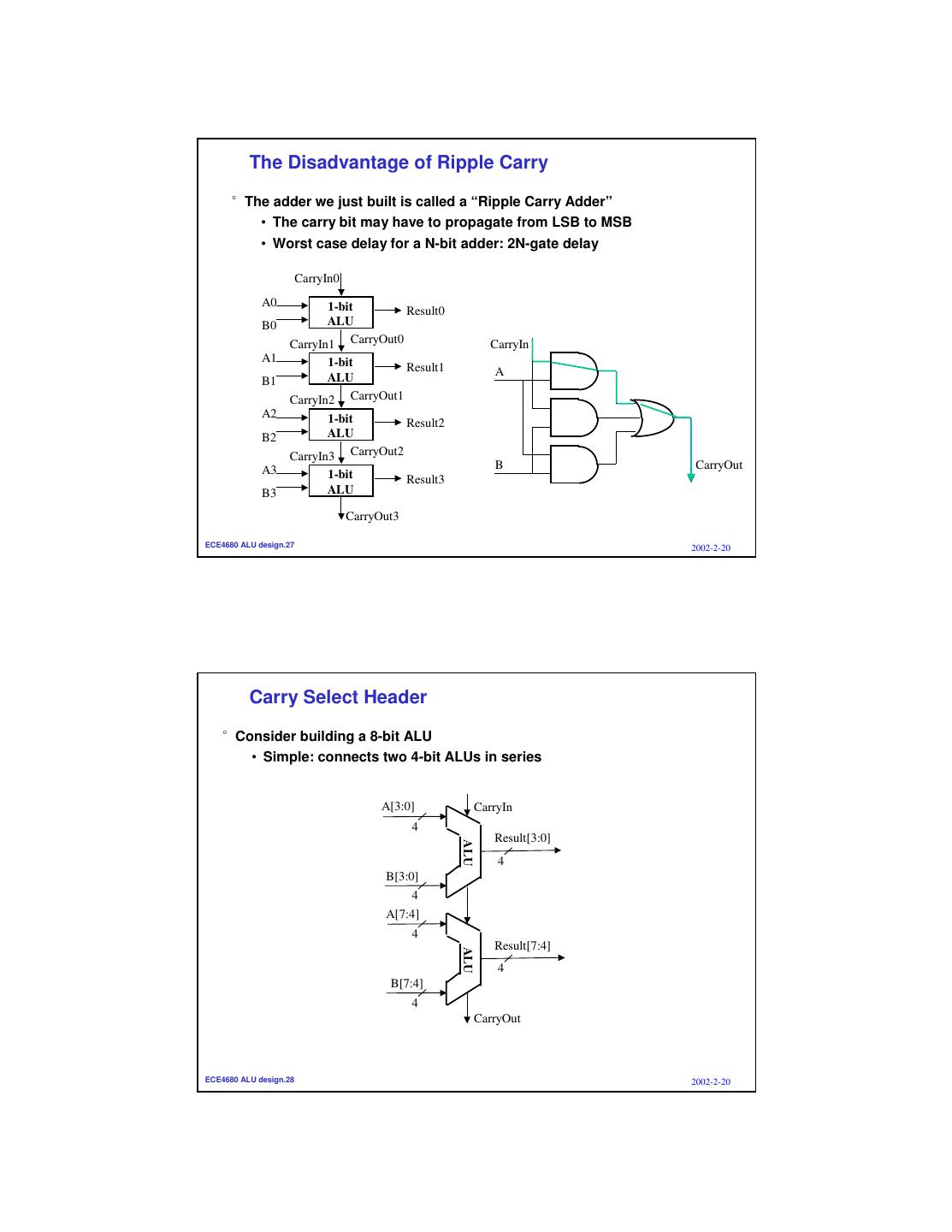
14 . The Disadvantage of Ripple Carry °The adder we just built is called a “Ripple Carry Adder” • The carry bit may have to propagate from LSB to MSB • Worst case delay for a N-bit adder: 2N-gate delay CarryIn0 A0 1-bit Result0 B0 ALU CarryIn1 CarryOut0 CarryIn A1 1-bit Result1 A B1 ALU CarryIn2 CarryOut1 A2 1-bit Result2 B2 ALU CarryIn3 CarryOut2 A3 B CarryOut 1-bit Result3 B3 ALU CarryOut3 ECE4680 ALU design.27 2002-2-20 Carry Select Header °Consider building a 8-bit ALU • Simple: connects two 4-bit ALUs in series A[3:0] CarryIn 4 Result[3:0] ALU 4 B[3:0] 4 A[7:4] 4 Result[7:4] ALU 4 B[7:4] 4 CarryOut ECE4680 ALU design.28 2002-2-20
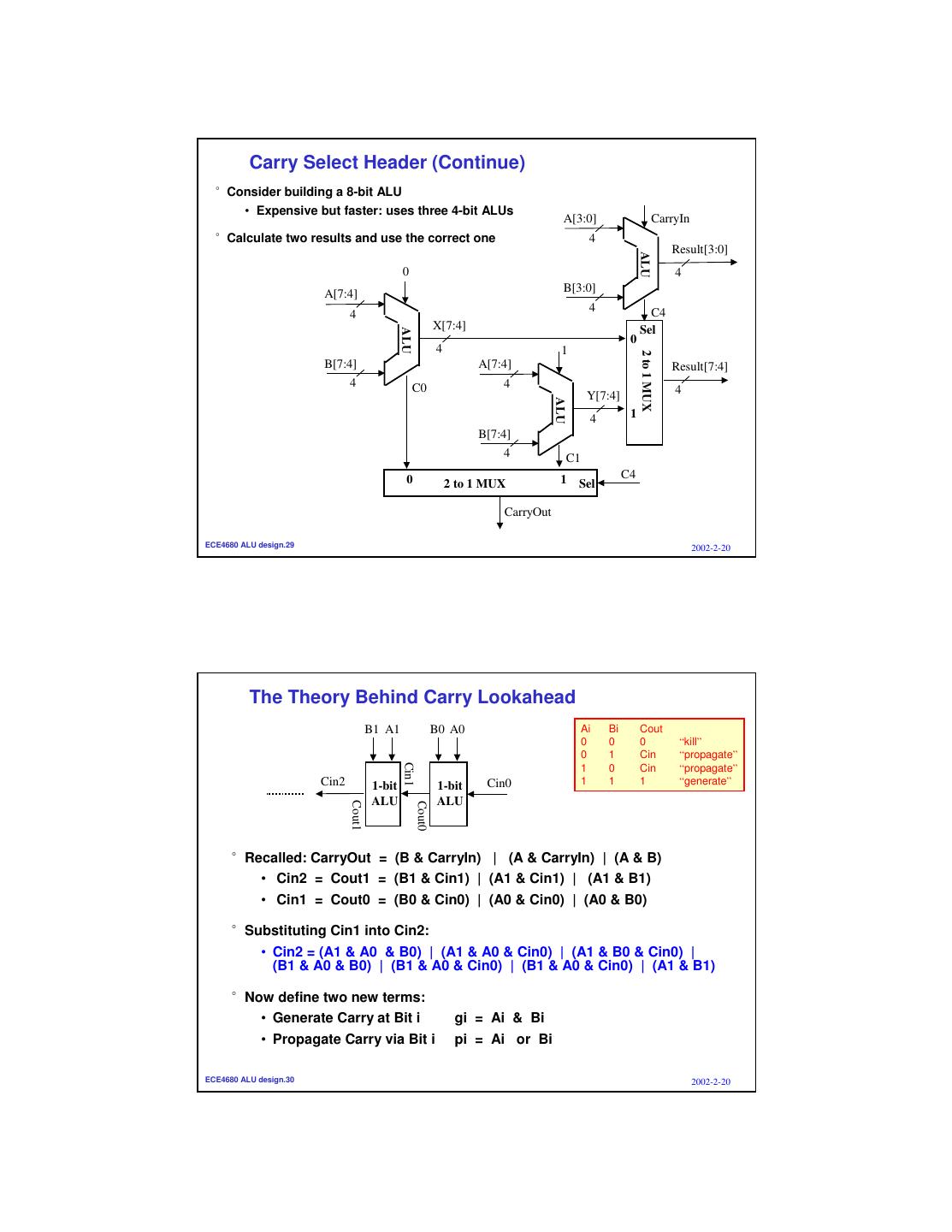
15 . Carry Select Header (Continue) °Consider building a 8-bit ALU • Expensive but faster: uses three 4-bit ALUs A[3:0] CarryIn °Calculate two results and use the correct one 4 Result[3:0] ALU 0 4 A[7:4] B[3:0] 4 C4 4 X[7:4] Sel ALU 0 4 1 2 to 1 MUX B[7:4] A[7:4] Result[7:4] 4 C0 4 Y[7:4] 4 ALU 4 1 B[7:4] 4 C1 0 1 Sel C4 2 to 1 MUX CarryOut ECE4680 ALU design.29 2002-2-20 The Theory Behind Carry Lookahead B1 A1 B0 A0 Ai Bi Cout 0 0 0 “kill” 0 1 Cin “propagate” Cin1 1 0 Cin “propagate” Cin2 1-bit 1-bit Cin0 1 1 1 “generate” ALU ALU Cout1 Cout0 °Recalled: CarryOut = (B & CarryIn) | (A & CarryIn) | (A & B) • Cin2 = Cout1 = (B1 & Cin1) | (A1 & Cin1) | (A1 & B1) • Cin1 = Cout0 = (B0 & Cin0) | (A0 & Cin0) | (A0 & B0) °Substituting Cin1 into Cin2: • Cin2 = (A1 & A0 & B0) | (A1 & A0 & Cin0) | (A1 & B0 & Cin0) | (B1 & A0 & B0) | (B1 & A0 & Cin0) | (B1 & A0 & Cin0) | (A1 & B1) °Now define two new terms: • Generate Carry at Bit i gi = Ai & Bi • Propagate Carry via Bit i pi = Ai or Bi ECE4680 ALU design.30 2002-2-20
16 . The Theory Behind Carry Lookahead (Continue) Ai Bi Cout °Using the two new terms we just defined: 0 0 0 “kill” • Generate Carry at Bit i gi = Ai & Bi 0 1 Cin “propagate” 1 0 Cin “propagate” • Propagate Carry via Bit i pi = Ai or Bi 1 1 1 “generate” °We can rewrite: • Cin1 = g0 | (p0 & Cin0) • Cin2 = g1 | (p1 & g0) | (p1 & p0 & Cin0) • Cin3 = g2 | (p2 & g1) | (p2 & p1 & g0) | (p2 & p1 & p0 & Cin0) °Carry going into bit 3 is 1 if • We generate a carry at bit 2 (g2) • Or we generate a carry at bit 1 (g1) and bit 2 allows it to propagate (p2 & g1) • Or we generate a carry at bit 0 (g0) and bit 1 as well as bit 2 allows it to propagate (p2 & p1 & g0) • Or we have a carry input at bit 0 (Cin0) and bit 0, 1, and 2 all allow it to propagate (p2 & p1 & p0 & Cin0) °Cini = f(g0,g1,…gi-1,p0,p1,…pi-1, Cin0) = f(A0,A1,…Ai-1,B0,B1,…Bi-1, Cin0) : Calculation of Cini can be quickly started since it is based on all initial inputs. All logical functions can be implemented by 2 levels of gates. ECE4680 ALU design.31 2002-2-20 Carry Lookahead Adder (Design trick: peek) Cini = f(g0,g1,…gi-1,p0,p1,…pi-1, Cin0) = f(A0,A1,…Ai-1,B0,B1,…Bi-1, Cin0) : Calculation of Cini can be quickly started since it is based on all initial inputs. All logical functions can be implemented by 2 levels of gates. CarryIn0 gi = Ai · Bi A0 1-bit pi = Ai + Bi Result0 B0 ALU g0 + p0 · Cin0 = Cin1 A1 1-bit Result1 B1 ALU g1 + p1 · g0 + p1 · p0 · Cin0 = Cin2 A2 1-bit Result2 B2 ALU g2 + p2 · g1 + p2 · p1 · g0 + p2 · p1 · p0 · Cin0 = Cin3 A3 1-bit Carry Lookahead Unit Result3 B3 ALU CarryOut3 ECE4680 ALU design.32 2002-2-20
17 . Compare Ripple Carry and Carry Lookahead Cini = f(A0,A1,…Ai-1,B0,B1,…Bi-1, Cin0) : Computation of Cini can be quickly started since it is based on all initial inputs. All logical functions can be implemented by 2 levels of gates. CarryIn0 Cin0 A0 1-bit A0 1-bit Result0 Result0 B0 ALU B0 ALU Cout0 Cin1 Carry Lookahead Unit Cin1 A1 1-bit A1 1-bit Result1 Result1 B1 ALU B1 ALU Cout1 Cin2 Cin2 A2 1-bit A2 1-bit Result2 Result2 B2 ALU B2 ALU Cout2 Cin3 Cin3 A3 1-bit A3 1-bit Result3 Result3 B3 ALU B3 ALU CarryOut3 CarryOut3 The sequential dependency of Ripple Carry is broken. All bits in Carry Lookahead can work in parallel. The delay of N-bit Carry Lookahead adder is always a constant of 4. But Imagine how expensive/complex the hardware would be! ECE4680 ALU design.33 2002-2-20 A Partial Carry Lookahead Adder °It is very expensive to build a “full” carry lookahead adder • Just imagine the length of the equation for Cin31 °Common practices: • Connects several N-bit Lookahead Adders to form a big adder • Example: connects four 8-bit carry lookahead adders to form a 32-bit partial carry lookahead adder A[31:24] B[31:24] A[23:16] B[23:16] A[15:8] B[15:8] A[7:0] B[7:0] 8 8 8 8 8 8 8 8 8-bit Carry C24 8-bit Carry C16 8-bit Carry C8 8-bit Carry C0 Lookahead Lookahead Lookahead Lookahead Adder Adder Adder Adder 8 8 8 8 Result[31:24] Result[23:16] Result[15:8] Result[7:0] ECE4680 ALU design.34 2002-2-20
18 . Hierarchical Carry Lookahead Adder Super Propagate Carry Super Generate Carry P0 = p3 & p2 & p1 & p0 G0 = g3 | p3&g2 | p3&p2&g1 | p3&p2&p1&g0 P1 = p7 & p6 & p5 & p4 G1 = g7 | p7&g6 | p7&p6&g5 | p7&p6&p5&g4 P2 = p11 & p10 & p9 & p8 G2 = g11| p11&g10 | p11&p10&g9 | p11&p10&p9&g8 P3 = p15 & p14 & p13 & p12 G3 = g15| p15&g14 | p15&p14&g13 | p15&p14&p13&g12 A[15:12] B[15:12] A[11:8] B[11:8] A[7:4] B[7:4] A[3:0] B[3:0] 4-bit ripple 4 4 4 4 4 4 4 4 carry adder 4-bit Carry 4-bit Carry 4-bit Carry 4-bit Carry c0 Lookahead Adder Lookahead Adder Lookahead Adder Lookahead Adder 4 4 4 4 C4 G3 P3 C3 G2 P2 C2 G1 P1 C1 G0 P0 carry-lookahead unit at higher level Result[15:12] Result[11:8] Result[7:4] Result[3:0] C1 = G0 | P0&c0 C2 = G1 | P1&G0 | P1&P0&c0 C3 = G2 | P2&G1 | P2&P1&G0 |P2&P1&P0&c0 C4 = G3 | P3&G2 | P3&P2&G1 |P3&P2&P1&G0 | P3&P2&P1&P0&c0 ECE4680 ALU design.35 2002-2-20 Summary °An Overview of the Design Process • Design is an iterative process-- successive refinement • Do NOT wait until you know everything before you start °An Introduction to Binary Arithmetics • If you use 2’s complement representation, subtract is easy. °ALU Design • Designing a Simple 4-bit ALU • Other ALU Construction Techniques °More information from Chapter 4 of the textbook ECE4680 ALU design.36 2002-2-20