1 .Strong Induction 2/27/12 1

2 .Induction Rule 2/27/12 2

3 .Strong Induction Rule 2/27/12 3

4 .Strong Induction Rule 2/27/12 3

5 .Fibonacci Numbers 0, 1, 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+ 5=8, … F n+1 =F n +F n-1 (n≥1) F 0 =0 F 1 =1 2/27/12 5

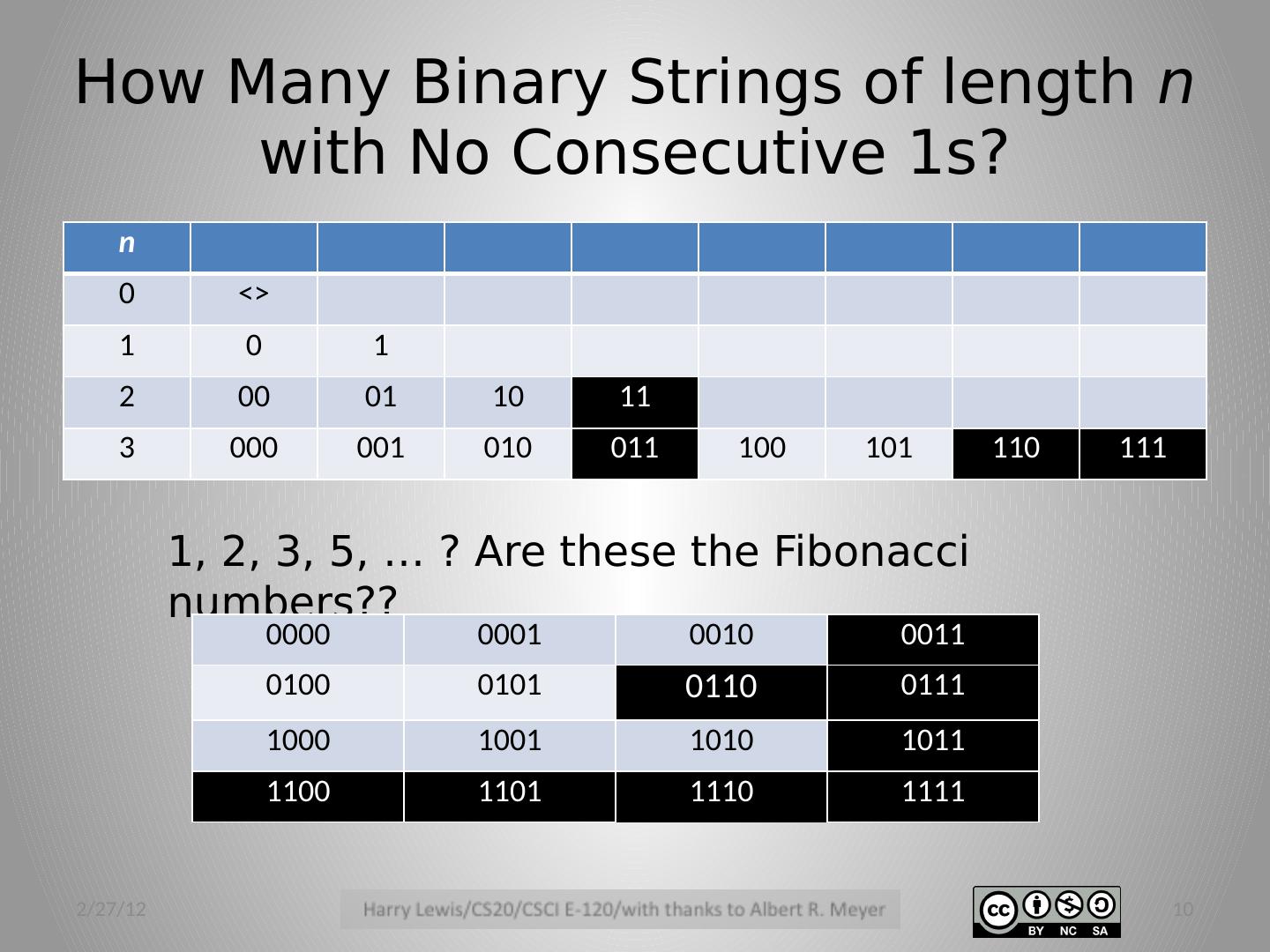
6 .How Many Binary Strings of length n with No Consecutive 1s? 2/27/12 6 n 0 <> 1 0 1 2 00 01 10 11 3 000 001 010 011 100 101 110 111

7 .How Many Binary Strings of length n with No Consecutive 1s? 2/27/12 7 n 0 <> 1 0 1 2 00 01 10 11 3 000 001 010 011 100 101 110 111

8 .How Many Binary Strings of length n with No Consecutive 1s? 2/27/12 8 n 0 <> 1 0 1 2 00 01 10 11 3 000 001 010 011 100 101 110 111

9 .How Many Binary Strings of length n with No Consecutive 1s? 2/27/12 9 n 0 <> 1 0 1 2 00 01 10 11 3 000 001 010 011 100 101 110 111

10 .How Many Binary Strings of length n with No Consecutive 1s? 2/27/12 10 n 0 <> 1 0 1 2 00 01 10 11 3 000 001 010 011 100 101 110 111 1, 2, 3, 5, … ? Are these the Fibonacci numbers?? 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

11 .C n = #Binary Strings of length n with No Consecutive 1s 2/27/12 11 n 0 1 2 3 4 C n 1 2 3 5 8 C n = F n +2 ?? Why would that be? Say that a string is “good” if it has no consecutive 1s Why would a “good” string of length n +1 have something to do with good strings of shorter length? n 0 1 2 3 4 5 6 F n 0 1 1 2 3 5 8

12 .Getting Good Strings of Length n +1 2/27/12 12 A good string of length n +1 ends in either 0 or 1. Call this good string x . [Try breaking the problem down into cases] If x ends in 0, the first n digits could be any good string of length n since adding a 0 to the end can’t turn a good string bad There are C n strings like that 0 Good string of length n x

13 .Getting Good Strings of Length n +1 2/27/12 13 If x ends in 1, the next to last digit must be 0 (otherwise x would end in 11 and be bad) But the previous n -1 digits could be any good string of length n -1. There are C n -1 strings like that Total = C n +1 = C n +C n -1 0 1 Good string of length n -1 x

14 .Proof by Induction that C n =F n +2 2/27/12 14 (Base cases) C 0 = 1 = F 0+2 C 1 = 2 = F 1+2 (Induction hypothesis) Assume n≥1 and C m =F m +2 for all m≤n . Need to show that C n +1 = F n +3 Then C n +1 = C n +C n -1 (by previous slide) = F n +2 +F n +1 (by the induction hypothesis) = F n +3 by defn of Fibonacci numbers

15 .Finis 2/27/12 15