展开查看详情
1 .States and Invariants 3/2/12 1
2 .State Space A state space is just a binary relation on a set S (the set of “states”) (Meyer calls this a “state machine”) E.g. S = 3x3 arrangements of X, O, blank a → b , where a , b ∈S, iff a move from state a can result in state b 3/2/12 2 X O X X O → → X X O O
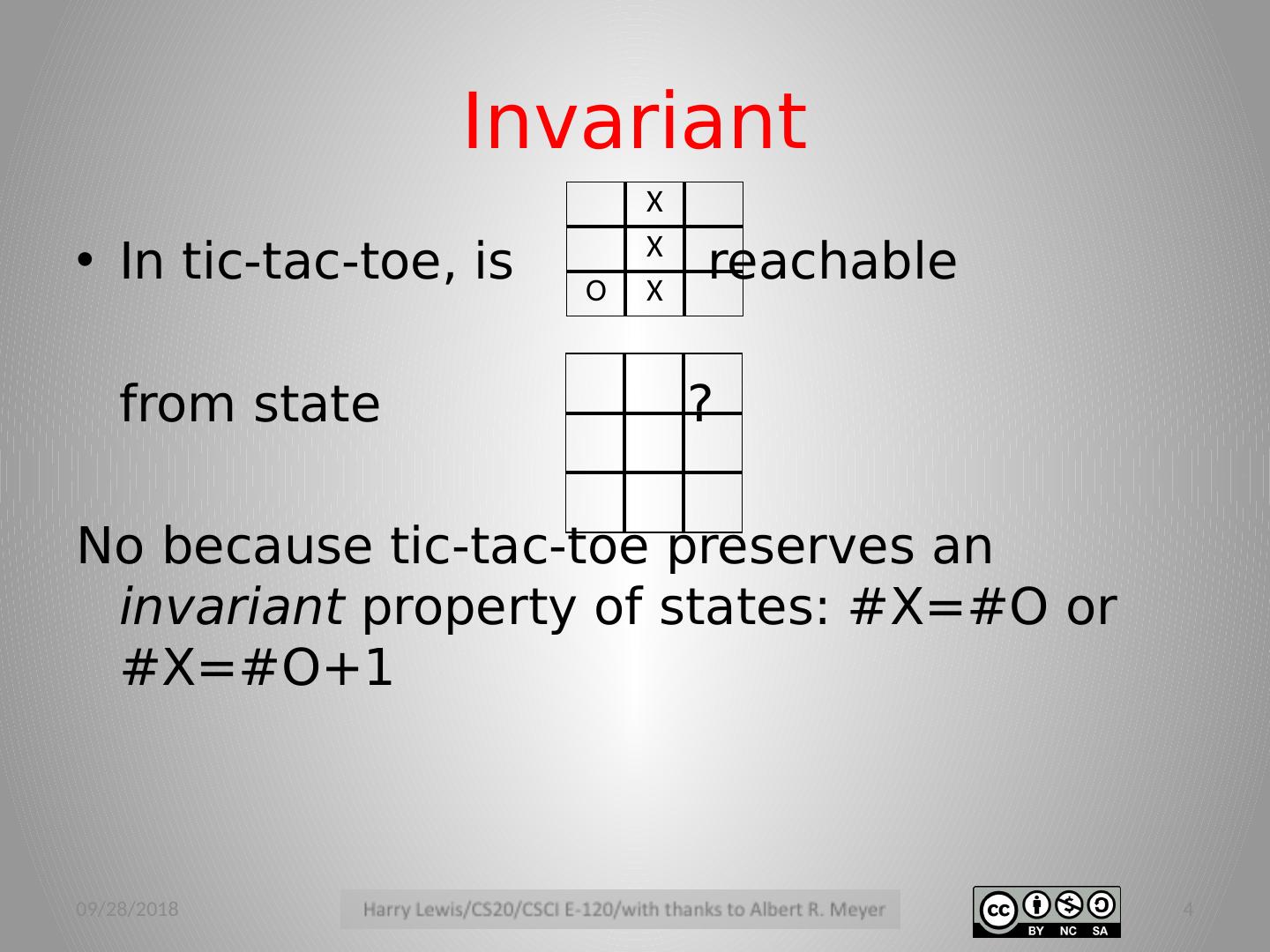
3 .Moving from state to state Many computational problems can be described in terms of the states that are reachable from a state after a series of moves In tic-tac-toe, is reachable from state ? 3/2/12 3 X X O X
4 .Invariant In tic-tac-toe, is reachable from state ? No because tic-tac-toe preserves an invariant property of states: #X=#O or #X=#O+1 3/2/12 4 X X O X
5 .Invariant Tic-tac-toe preserves an invariant property of states: #X=#O or #X=#O+1 #X = #O = 0: Initial state X always goes first a → b : state b is a successor of state a if #X=#O in a , then #X=#O+1 in b if #X=#O+1 in a , then #X=#O in b Therefore is unreachable. 3/2/12 5 X X O X
6 .Floyd’s Invariant Principle Preserved Invariant , P ( state ): if P ( q ) and ,then P ( r ) Conclusion: if P ( start ), then P ( r ) for all reachable states r , including final state (if any) q r 3/2/12 6
7 .Computing Factorials n ! = n∙(n-1)∙…∙2∙1 Let b :=1, a:= n If a=1 then return b b := b∙a a:=a-1 Go to step 2 To prove Correctness (if it computes anything it computes n !): Let state set S = N×N×N : the values of (a, b , n ) (a, b , n ) → (a-1, a∙b , n ) in each iteration of loop steps 2-5 Let P(a , b , n ) ≡ “a! ∙ b = n !” Show P(n , 1, n ) P(a , b , n ) ⇒P(a-1, a∙b , n ) , because a! ∙ b = n ⇒ (a-1)! ∙ ( a∙b ) = n ! So the loop preserves the invariant P(a , b , n ) When & if a=1, since P(1, b , n ) is true, b must be n ! 3/2/12 7
8 .Computing Factorials n ! = n∙(n-1)∙…∙2∙1 If the program computes anything it computes n ! But still must show Termination: a initially is n and decreases by 1 on each iteration and therefore must eventually reach 1 PROVIDED n≥1 !! 3/2/12 8 Let b :=1, a:= n If a=1 then return b b := b∙a a:=a-1 Go to step 2
热门城市
