State Machine

1 .Chapter 3 Digital Logic Structures

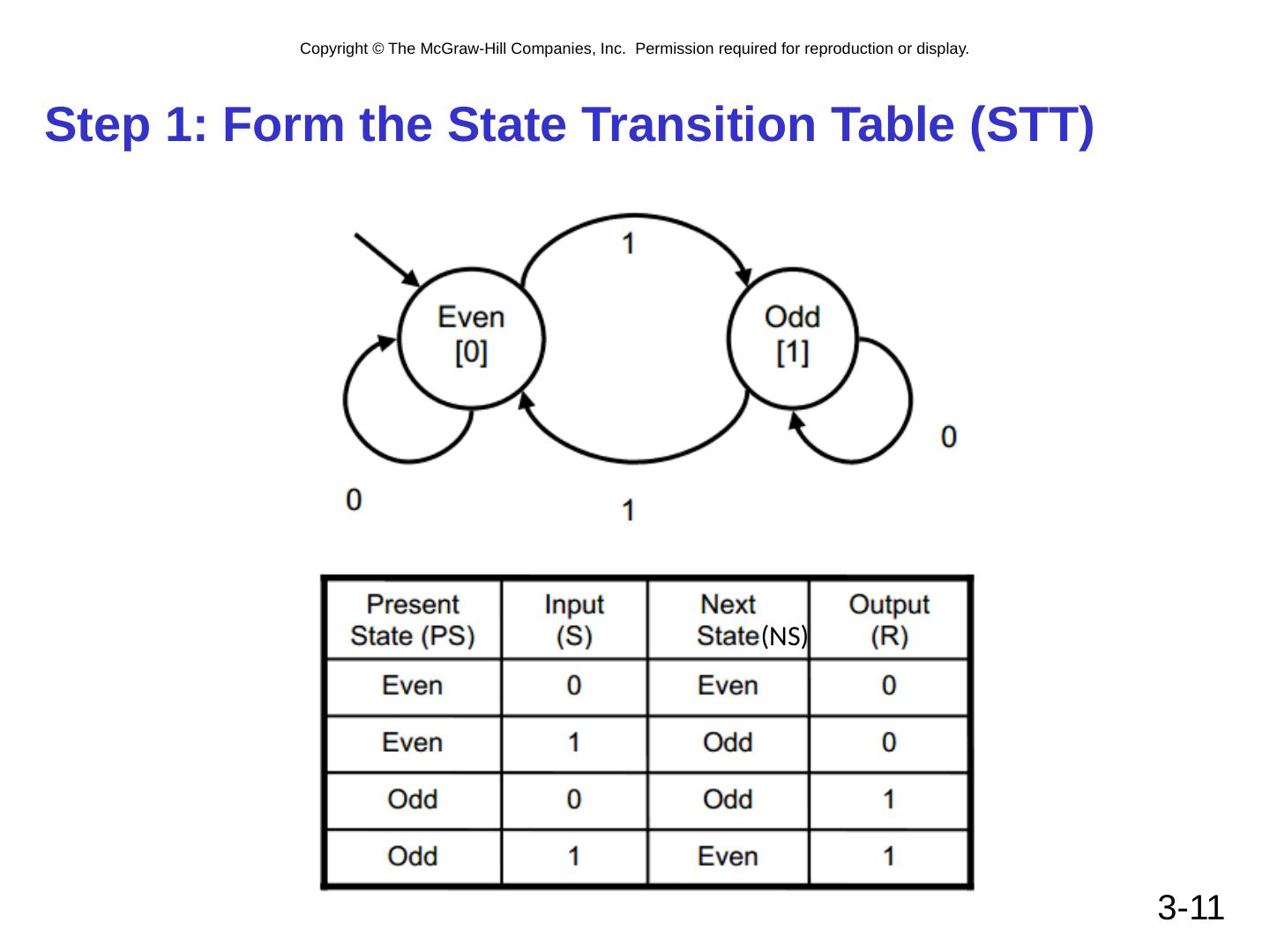
2 .3- 2 State Machine Another type of sequential circuit Combines combinational logic with storage “Remembers” state, and changes output (and state) based on inputs and current state

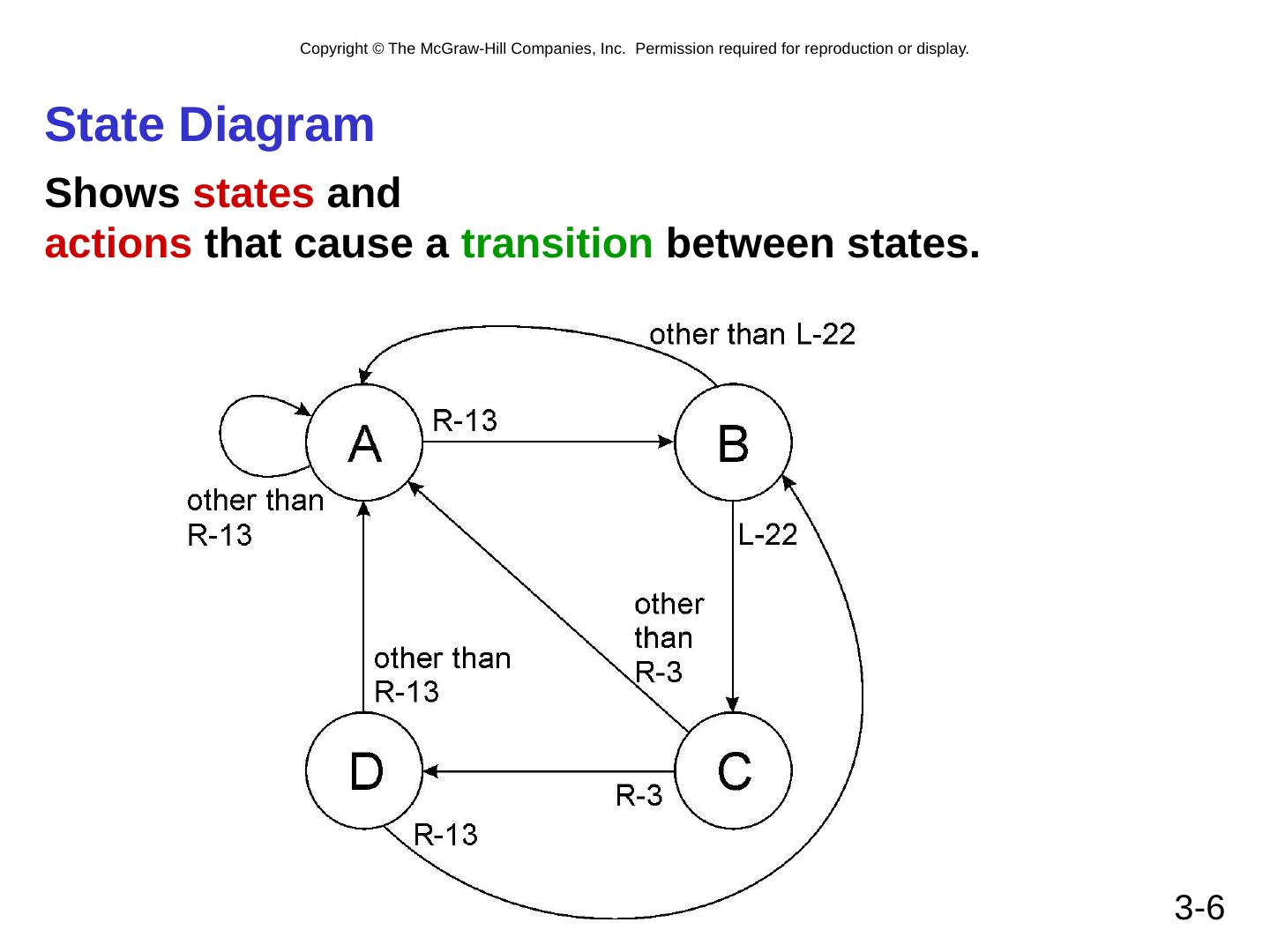
3 .3- 3 Combinational vs. Sequential Two types of “combination” locks 4 1 8 4 30 15 5 10 20 25 Combinational Success depends only on the values , not the order in which they are set. Sequential Success depends on the sequence of values (e.g, R-13, L-22, R-3).

4 .3- 4 State The state of a system is a snapshot of all the relevant elements of the system at the moment the snapshot is taken. Examples: The state of a basketball game can be represented by the scoreboard. Number of points, time remaining, possession, etc. The state of a tic-tac-toe game can be represented by the placement of X’s and O’s on the board.

5 .3- 5 State of Sequential Lock Our lock example has four different states, labelled A-D: A: The lock is not open , and no relevant operations have been performed. B: The lock is not open , and the user has completed the R-13 operation. C: The lock is not open , and the user has completed R-13 , followed by L-22 . D: The lock is open . (user has completed R-13 , L-22 and then R-3 )

6 .3- 6 State Diagram Shows states and actions that cause a transition between states.

7 .Definition of a Finite State Machine A set of input events A set of output events A set of states A function that maps states and input to output A function that maps states and inputs to states (which is called a state transition function ) Must be complete A description of the initial state A finite state machine is one that has a limited or finite number of possible states.  3- 7

8 .Example 2: A Door Combination Lock 3- 8 Partial Complete entry code is the 4-bit sequence “0110”

9 .Example 3: Odd Parity Checker 3- 9

10 .Why Finite State Machines (FSMs) A FSM is simple and intuitive way of describing a system which has discrete dynamics (State Transition Diagrams). An FSM is an “abstract machine.” That means that we use a mathematical description of the machine to reason about it without actually building it. A FSM can be directly and unambiguously converted into a digital electronic circuits .  3- 10

11 .Step 1: Form the State Transition Table (STT) 3- 11 (NS)

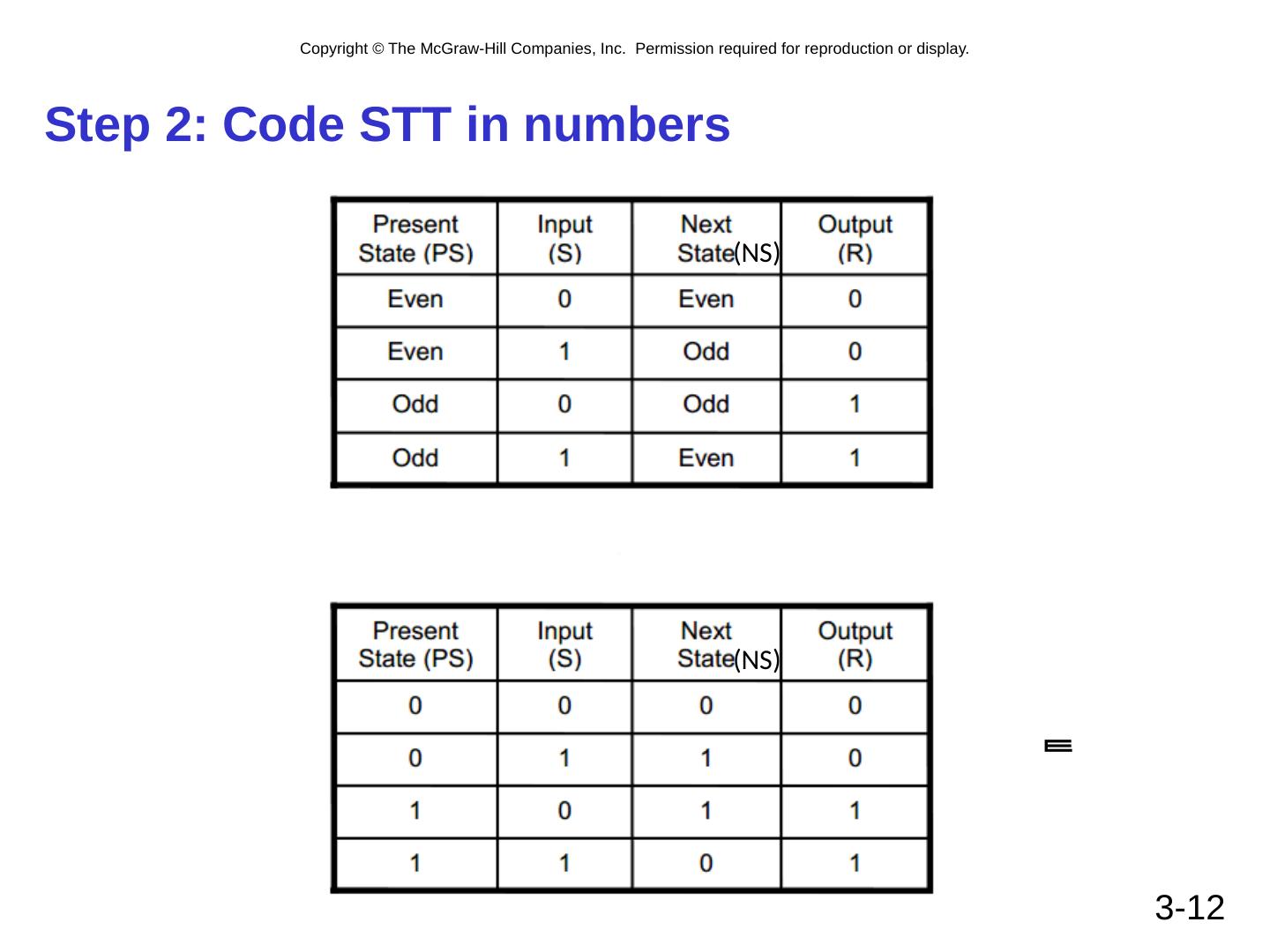
12 .Step 2: Code STT in numbers 3- 12  (NS) (NS)

13 .Step 3: Implement STT 3- 13

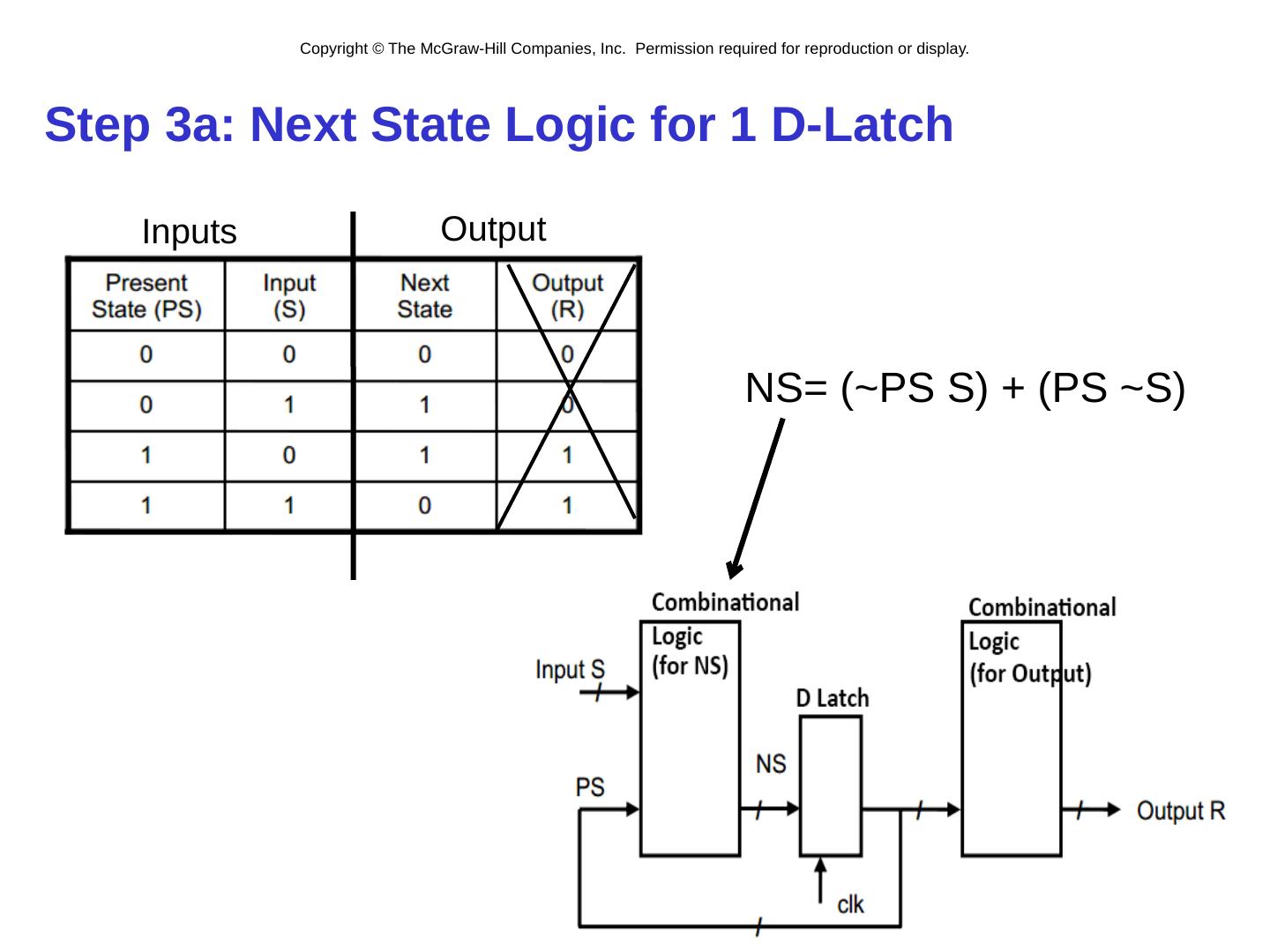
14 .Step 3a: Next State Logic for 1 D-Latch 3- 14 NS= (~PS S) + (PS ~S) Inputs Output

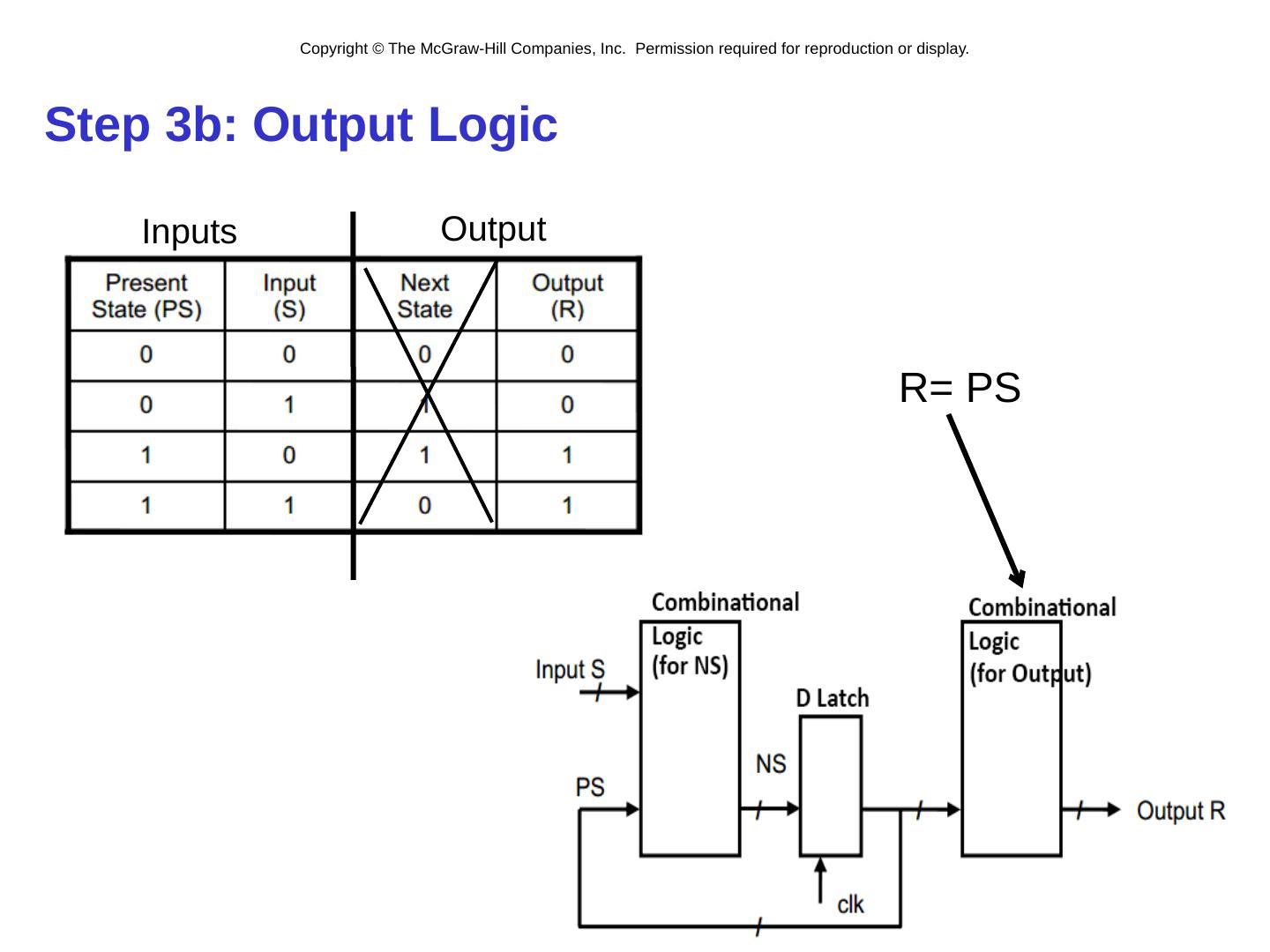
15 .Step 3b: Output Logic 3- 15 R = PS Inputs Output

16 .Step 4: Implement Circuit 3- 16

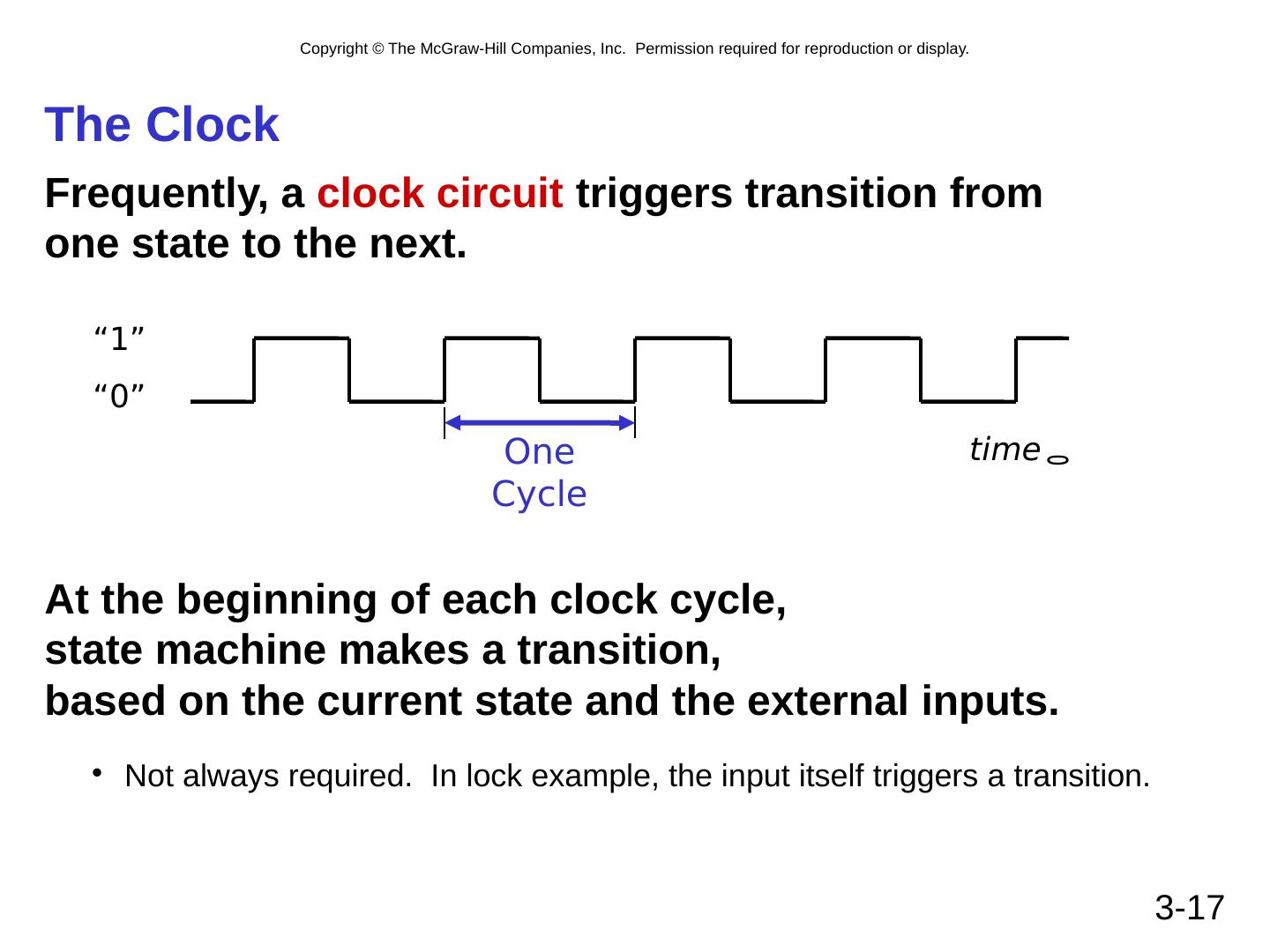
17 .3- 17 The Clock Frequently, a clock circuit triggers transition from one state to the next. At the beginning of each clock cycle, state machine makes a transition, based on the current state and the external inputs. Not always required. In lock example, the input itself triggers a transition. “1” “0” time  One Cycle

18 .3- 18 Master-Slave Flipflop A pair of gated D-latches, to isolate next state from current state. During 1 st phase (clock=1), previously-computed state becomes current state and is sent to the logic circuit. During 2 nd phase (clock=0), next state, computed by logic circuit, is stored in Latch A. PS N S PS