- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
系列
展开查看详情
1 .Series Geometric Series Binomial Coefficients Harmonic Series
2 .Sum of a Geometric Series What is Method 1: Prove by induction that for every n≥0, And then make some argument about the limit as n →∞ to conclude that the sum is 2.
3 .Sum of a Geometric Series Another way. Recall that and plug in x = ½ ! These “formal power series” have many uses.
4 .Another example What is Since
5 .Another Example What is Generalize. Note that S=F(1/3) where
6 .Manipulating Power Series
7 .Another Approach But then
8 .Identities involving “Choose” What is “Set Theory” derivation Let S be a set of size n This is the sum of the number of 0 element subsets, plus the number of 1-element subsets, plus …, plus the number of n -element subsets Total 2 n
9 .Binomial Theorem because if you multiply out ( x+y)(x+y)(x+y )…( x+y ) the coefficient of x i y n-i is the number of different ways of choosing x from i factors and y from n-i factors
10 .Using the Binomial Theorem Since substituting x = y =1 yields
11 .Using the Binomial Theorem What is Try to make this look like the binomial thm
12 .Stacking books Can you stack identical books so the top one is completely off the table? 4/12/12
13 .Stacking books Can you stack identical books so the top one is completely off the table? One book: balance at middle 4/12/12 1 1
14 .Stacking books Two books: balance top one at the middle, the second over the table edge at the center of gravity of the pair 4/12/12 1 1 1 ½
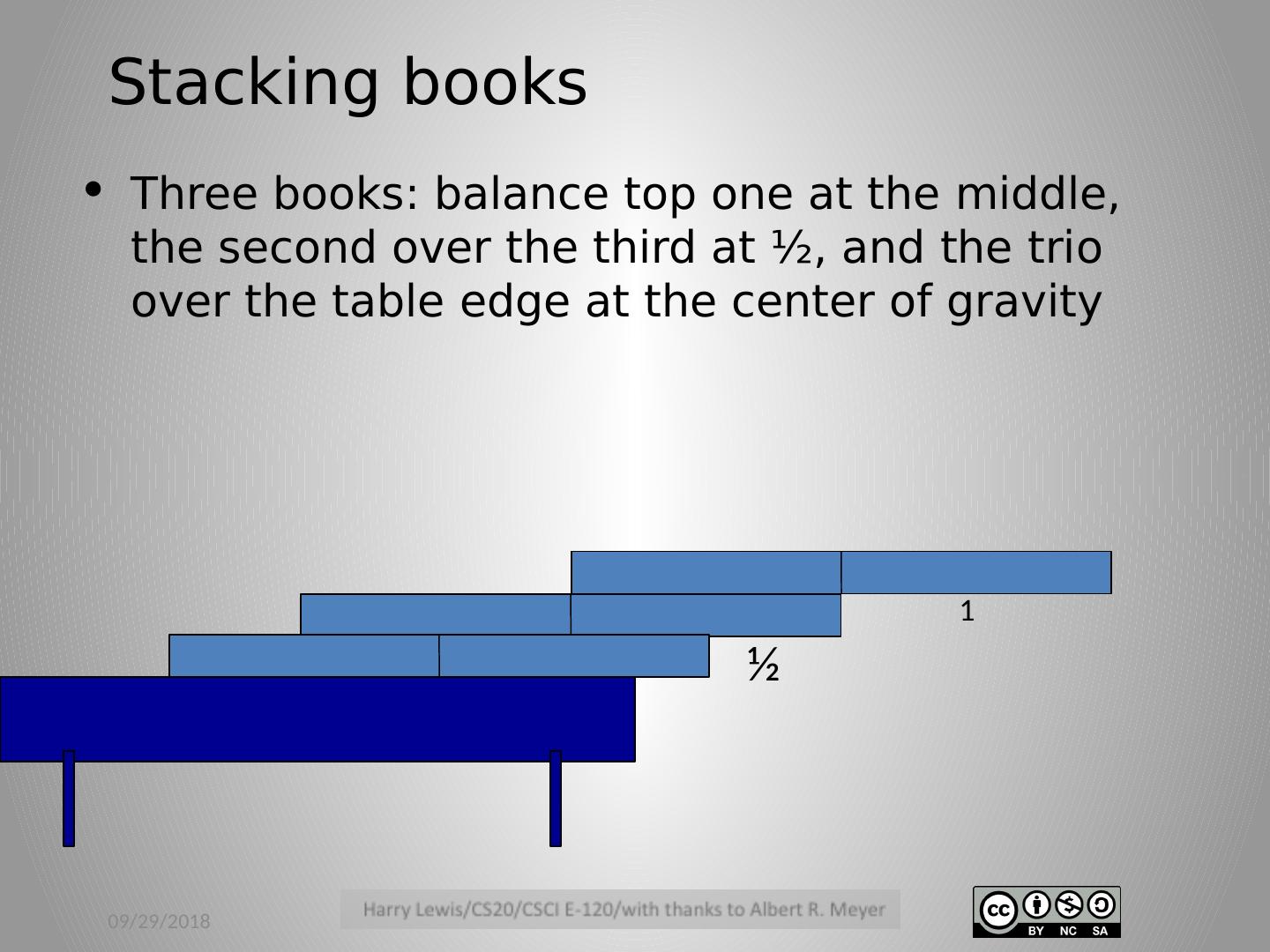
15 .Stacking books Three books: balance top one at the middle, the second over the third at ½, and the trio over the table edge at the center of gravity 4/12/12 1 ½
16 .Stacking books Three books: balance top one at the middle, the second over the third at ½, and the trio over the table edge at the center of gravity = (1+2+2½)/3 = 1⅚ from right end 4/12/12 1 ½ 1⅚
17 .Stacking books Three books: balance top one at the middle, the second over the third at ½, and the trio over the table edge at the center of gravity = (1+2+2½)/3 = 1⅚ from right end 4/12/12 1 ½ ⅓ 1⅚ See a pattern?
18 .The Harmonic Series Diverges Let . Then for any n, Doubling the number of terms adds at least ½ to the sum Corollary. The series diverges, that is, 4/12/12
19 .Proof by WOP that the Harmonic Series Diverges 4/12/12
20 .The Harmonic Series Diverges 4/12/12
21 .So w ith a stack of 31 books you get 2 book lengths off the table! And there is no limit to how far the stack can extend ! 4/12/12 http://mathforum.org/advanced/robertd/harmonic.html
22 .FINIS