抽样分布

1 .5-2: 抽样分布 张伟平 

2 .第五章: 数理统计的基本概念与抽样分布 4.1 三大分布 . . . . . . . . . . . . . . . . . . . . 1 4.1.1 χ 分布 . . . . . . . . . . . . . . . . . 2 1 4.1.2 t 分布 . . . . . . . . . . . . . . . . . . 7 4.1.3 F 分布 . . . . . . . . . . . . . . . . . 12 4.1.4 正态总体样本均值和样本方差的分布 . 16 4.1.5 几个重要推论 . . . . . . . . . . . . . . 18 4.2 总结 . . . . . . . . . . . . . . . . . . . . . . . 23 Previous Next First Last Back Forward 1 

3 . 4.1 三大分布 能求出抽样分布的确切而且具有简单表达式的情形并不多, 一般 都较难. 所幸的是, 在总体分布为正态情形, 许多重要统计量的抽样分 布可以求得, 这些多与下面讨论的三种分布有密切关系. 这三个分布 在后面几章中有重要应用. 4.1.1 χ2 分布 ∑ n 设 X1 , X2 , · · · , Xn i.i.d. ∼ N (0, 1), 令 X = Xi2 , 则称 i=1 Definition X 是自由度为 n 的 χ2 变量, 其分布称为自由度为 n 的χ2 分布, 记为 X ∼ χ2n . Previous Next First Last Back Forward 1 

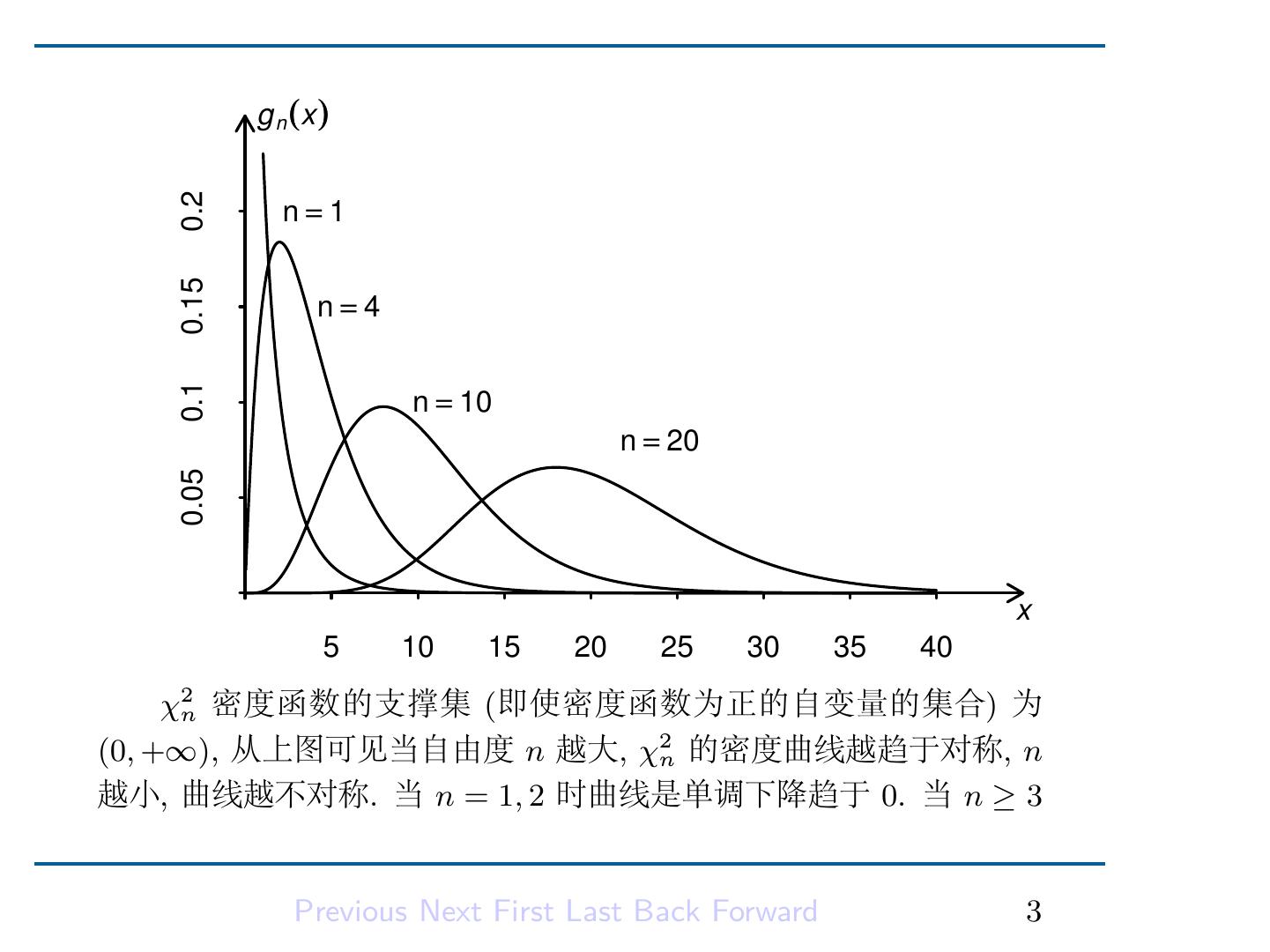
4 . 设随机变量 X 是自由度为 n 的 χ2 随机变量, 则其概率密度函 数为   n 1 n x x 2 −1 e− 2 , x > 0, gn (x) = 2 2 Γ( n 2 ) (4.1)  0, x ≤ 0. χ2n 的密度函数 gn (x) 形状如下图 Previous Next First Last Back Forward 2 

5 . g n (x ) 0.2 n=1 0.15 n=4 0.1 n = 10 n = 20 0.05 x 5 10 15 20 25 30 35 40 χ2n 密度函数的支撑集 (即使密度函数为正的自变量的集合) 为 (0, +∞), 从上图可见当自由度 n 越大, χ2n 的密度曲线越趋于对称, n 越小, 曲线越不对称. 当 n = 1, 2 时曲线是单调下降趋于 0. 当 n ≥ 3 Previous Next First Last Back Forward 3 

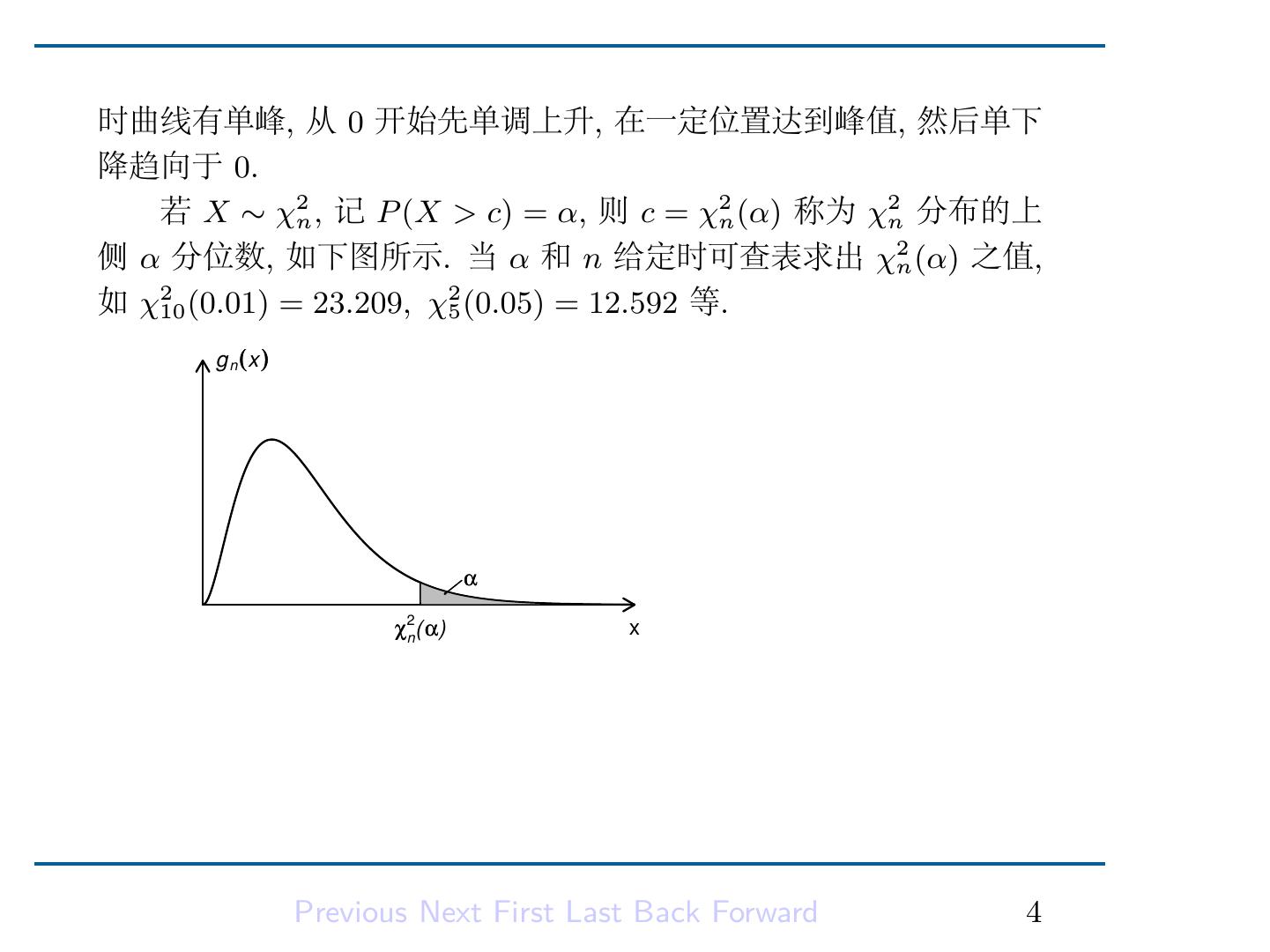
6 .时曲线有单峰, 从 0 开始先单调上升, 在一定位置达到峰值, 然后单下 降趋向于 0. 若 X ∼ χ2n , 记 P (X > c) = α, 则 c = χ2n (α) 称为 χ2n 分布的上 侧 α 分位数, 如下图所示. 当 α 和 n 给定时可查表求出 χ2n (α) 之值, 如 χ210 (0.01) = 23.209, χ25 (0.05) = 12.592 等. g n (x ) α χ2n( α) x Previous Next First Last Back Forward 4 

7 . χ2 变量具有下列性质: (1) 设随机变量 X ∼ χ2n 则有 E(X) = n, V ar(X) = 2n. (2) 设 Z1 ∼ χ2n1 , Z2 ∼ χ2n2 , 且 Z1 和 Z2 独立, 则 Z1 + Z2 ∼ χ2n1 +n2 . 我们从 X 2 分布的定义出发给出一个简单证明: 由定义 Z1 = X12 + · · · + Xn21 , 此处 X1 , X2 , · · · , Xn1 i.i.d. ∼ N (0, 1), 同理 Z2 = Xn21 +1 + · · · + Xn21 +n2 , 此处 Xn1 +1 , Xn1 +2 , · · · , Xn1 +n2 i.i.d. ∼ N (0, 1), Previous Next First Last Back Forward 5 

8 .再由 Z1 和 Z2 的独立性可知 X1 , X2 , · · · , Xn1 �Xn1 +1 , · · · , Xn1 +n2 i.i.d. ∼ N (0, 1). 因此 Z1 + Z2 = X12 + · · · + Xn21 + Xn21 +1 + · · · + Xn21 +n2 . 按定义即有 Z1 + Z2 ∼ χ2n1 +n2 . Previous Next First Last Back Forward 6 

9 .4.1.2 t 分布 设随机变量 X ∼ N (0, 1), Y ∼ χ2n , 且 X 和 Y 独立, 则称 X T = √ Y /n Definition 为自由为 n 的 t 变量, 其分布称为由为 n 的t 分布, 记为 T ∼ tn . 设随机变量 T ∼ tn , 则其密度函数为 ( )− n+1 Γ( n+1 ) x2 2 n √ , −∞<x<∞ 2 tn (x) = 1+ (4.2) Γ( 2 ) nπ n 该密度函数的图形如下 Previous Next First Last Back Forward 7 

10 . tn(x) N (0,, 1)(t ∞(x )) 0.4 t 10(x ) t 5(x ) 0.3 t 1(x ) 0.2 0.1 x −4 −3 −2 −1 0 1 2 3 4 Previous Next First Last Back Forward 8 

11 . tn 的密度函数与标准正态分布 N (0, 1) 密度很相似, 它们都是关 于原点对称, 单峰偶函数, 在 x = 0 处达到极大. 但 tn 的峰值低于 N (0, 1) 的峰值, tn 的密度函数尾部都要比 N (0, 1) 的两侧尾部粗一 些. 容易证明: lim tn (x) = φ(x) n→∞ 此处 φ(x) 是 N (0, 1) 变量的密度函数. Previous Next First Last Back Forward 9 

12 . t n (x ) α 2 α 2 − t n ( α 2) t n ( α 2) x 若 T ∼ tn , 记 P (|T | > c) = α, 则 c = tn (α/2) 为自由度为 n 的 t 分布的双侧 α 分位数 (如上图所示). 当给定 α 时, tn (α), tn (α/2) 等可通过查表求出. 例如 t12 (0.05) = 1.782, t9 (0.025) = 2.262 等. t 分布是英国统计学家 W.S. Gosset 在 1908 年以笔名 Student Previous Next First Last Back Forward 10 

13 .发表的论文中提出的, 故后人称为 “学生氏 (Student) 分布” 或 “t 分 布”. t 变量具有下列的性质: (1) 若随机变量 T ∼ tn , 则当 n ≥ 2 时, E(T ) = 0. 当 n ≥ 3 时, V ar(T ) = n n−2 . (2) 当 n → ∞ 时, t 变量的极限分布为 N (0, 1). Previous Next First Last Back Forward 11 

14 .4.1.3 F 分布 设随机变量 X ∼ χ2m , Y ∼ χ2n , 且 X 和 Y 独立, 则称 X/m F = Y /n Definition 为自由度分别是 m 和 n 的 F 变量, 其分布称为自由度分 别是 m 和 n 的F 分布, 记为 F ∼ Fm,n . 若随机变量 Z ∼ Fm,n , 则其密度函数为   Γ( m+n ) m n m m+n Γ( n 2 )Γ( m ) m 2 n 2 x 2 −1 (n + mx)− 2 , x > 0, fm,n (x) = 2 2 0, 其它. (4.3) Previous Next First Last Back Forward 12 

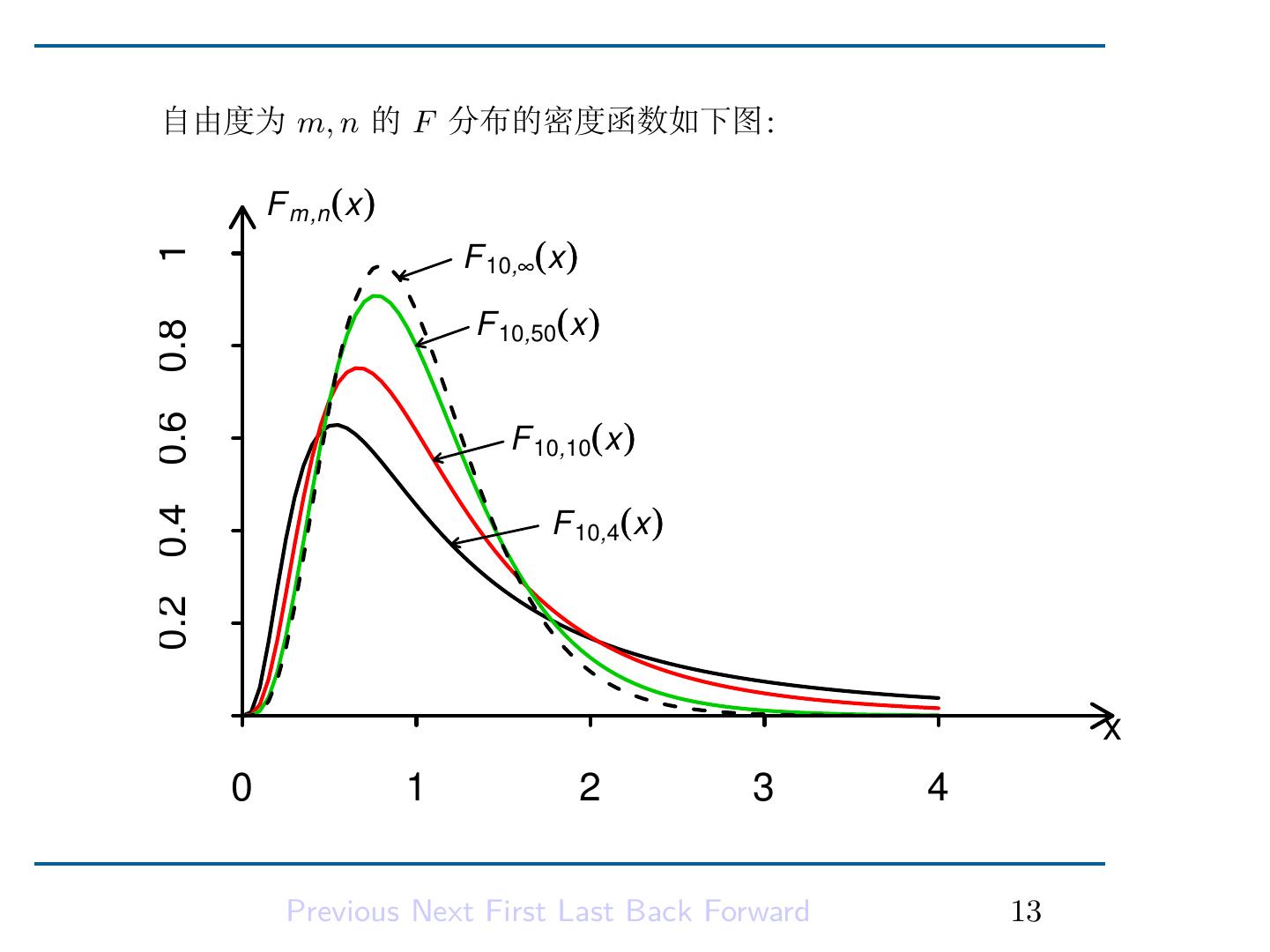
15 . 自由度为 m, n 的 F 分布的密度函数如下图： F m,n (x ) F 10,∞∞(x ) 1 F 10,50(x ) 0.2 0.4 0.6 0.8 F 10,10(x ) F 10,4(x ) x 0 1 2 3 4 Previous Next First Last Back Forward 13 

16 . 注意 F 分布的自由度 m 和 n 是有顺序的, 当 m ̸= n 时若将自 由度 m 和 n 的顺序颠倒一下, 得到的是两个不同的 F 分布. 从上图 可见对给定 m = 10, n 取不同值时 fm,n (x) 的形状, 我们看到曲线是 偏态的, n 越小偏态越严重. F m,n (x ) α F m,n (α) x 若 F ∼ Fm,n , 记 P (F > c) = α, 则 c = Fm,n (α) 称为 F 分布 的上侧 α 分位数 (见上图). 当 m, n 和 α 给定时, 可以通过查表求出 Fm,n (α) 之值, 例如 F4,10 (0.05) = 3.48, F10,15 (0.01) = 3.80 等. 这 Previous Next First Last Back Forward 14 

17 .在区间估计和假设检验问题中常常用到. F 变量具有下列的性质: / (1) 若 Z ∼ Fm,n , 则 1 Z ∼ Fn,m . (2) 若 T ∼ tn , 则 T 2 ∼ F1,n / (3) Fm,n (1 − α) = 1 Fn,m (α) 以上性质中 (1) 和 (2) 是显然的, (3) 的证明不难. 尤其性质 (3) 在求区间估计和假设检验问题时会常常用到. 因为当 α 为较小的数, 如 α = 0.05 或 α = 0.01, m, n 给定时, 从已有的 F 分布表上查不 到 Fm,n (1 − 0.05) 和 Fm,n (1 − 0.01) 之值, 但它们的值可利用性质 (3) 求得, 因为 Fn,m (0.05) 和 Fn,m (0.01) 是可以通过查 F 分布表求 得的. Previous Next First Last Back Forward 15 

18 .4.1.4 正态总体样本均值和样本方差的分布 为方便讨论正态总体样本均值和样本方差的分布, 我们先给出正 态随机变量的线性函数的分布. 1. 正态变量线性函数的分布 设随机变量 X1 , · · · , Xn i.i.d. ∼ N (a, σ 2 ), c1 , c2 , · · · , cn 为常 数, 则有 ∑ n ( ∑ n ∑ n ) T = ck Xk ∼ N a ck , σ 2 c2k k=1 k=1 k=1 ∑ n 特别, 当 c1 = · · · = cn = 1/n, 即 T = 1 n ¯ 时, 有 Xi = X i=1 / ¯ ∼ N (a, σ 2 n). X Previous Next First Last Back Forward 16 

19 .2. 正态变量样本均值和样本方差的分布 下述定理给出了正态变量样本均值和样本方差的分布和它们的独 立性. ∑ n 定理 1. 设 X1 , X2 , · · · , Xn i.i.d. ∼ N (a, σ 2 ), X ¯ = 1 n Xi 和 S 2 = i=1 ∑ n 1 n−1 (Xi − X) ¯ 2 分别为样本均值和样本方差, 则有 i=1 (1) X¯ ∼ N (a, 1 σ 2 ); n (2) (n − 1)S 2 /σ 2 ∼ χ2n−1 ; (3) X¯ 和 S 2 独立. Previous Next First Last Back Forward 17 

20 .4.1.5 几个重要推论 下面几个推论在正态总体区间估计和假设检验问题中有着重要应 用. 推论 1. 设 X1 , X2 , · · · , Xn 相互独立相同分布 (i.i.d.) ∼ N (a, σ 2 ), 则 √ ¯ n(X − a) T = ∼ tn−1 . S 证: 由注 5.4.3 可知 X ¯ ∼ N (a, σ 2 /n), 将其标准化得 √n(X ¯ − a)/σ ∼ N (0, 1). 又 (n − 1)S /σ ∼ χn−1 , 即 S /σ ∼ χn−1 /(n − 1), 且 X 2 2 2 2 2 2 ¯ 2 和 S 独立, 按定义有 √ ¯ √ ¯ n(X − a)/σ n(X − a) T = √ = ∼ tn−1 . 2 S /σ 2 S Previous Next First Last Back Forward 18 

21 .推论 2. 设 X1 , X2 , · · · , Xm i.i.d. ∼ N (a1 , σ12 ), Y1 , Y2 , · · · , Yn i.i.d. ∼ N (a2 , σ22 ), 且假定 σ12 = σ22 = σ 2 , 样本 X1 , X2 , · · · , Xm 与 Y1 , Y2 , · · · , Yn 独立, 则 √ ¯ − Y¯ ) − (a1 − a2 ) (X mn T = · ∼ tn+m−2 , Sw n+m 此处 (n + m − 2)Sw2 = (m − 1)S12 + (n − 1)S22 , 其中 1 ∑m 1 ∑ n S12 = (Xi − X) ¯ 2, S22 = (Yj − Y¯ )2 . m − 1 i=1 n − 1 j=1 证: 由注 5.4.3 可知 X ¯ ∼ N (a, σ 2 /m), Y¯ ∼ N (a2 , σ 2 /n), 故有 X¯− ( ) ( ) Y¯ ∼ N a1 − a2 , ( m + n )σ = N a1 − a2 , mn σ . 将其标准化得 1 1 2 n+m 2 √ X¯ − Y¯ − (a1 − a2 ) mn ∼ N (0, 1). (4.4) σ m+n 又 (m − 1)S12 /σ 2 ∼ χ2m−1 , (n − 1)S22 /σ 2 ∼ χ2n−1 , 再利用 χ2 分布的 性质可知 (m − 1)S12 + (n − 1)S22 ∼ χ2n+m−2 . (4.5) σ2 Previous Next First Last Back Forward 19 

22 . ¯ Y¯ ) 与 (S12 , S22 ) 相互独立, 由定义可知 再由 (4.4) 和 (4.5) 中 (X, √ /√ ¯ − Y¯ ) − (a1 − a2 ) (X mn (m − 1)S12 + (n − 1)S22 T = σ n+m σ 2 (n + m − 2) √ ¯ − Y¯ ) − (a1 − a2 ) (X nm = ∼ tn+m−2 . Sw n+m 推论 3. 设 X1 , X2 , · · · , Xm i.i.d. ∼ N (a1 , σ12 ), Y1 , Y2 , · · · , Yn i.i.d. ∼ N (a2 , σ22 ), 且合样本 X1 , X2 , · · · , Xm 和 Y1 , Y2 , · · · , Yn 相互独立, 则 S12 σ22 F = · ∼ Fm−1,n−1 , S22 σ12 此处 S12 和 S22 定义如推论2所述. 证: 由注 5.4.3 可知 (m − 1)SX 2 /σ12 ∼ χ2m−1 , (n − 1)SY2 /σ22 ∼ χ2n−1 , Previous Next First Last Back Forward 20 

23 .且二者独立, 由 F 分布的定义可知 2 (m−1)SX / 2 σ1 (m − 1) S 2 σ22 F = 2 / = X · ∼ Fm−1,n−1 . (n−1)SY (n − 1) SY2 σ12 2 σ2 证毕. 下列这一推论给出了服从指数分布随机变量的线性函数的分布与 χ2 分布的关系. 这在指数分布总体的区间估计和假设检验问题中有 重要应用. 推论 4. 设 X1 , X2 , · · · , Xn i.i.d. 服从指数分布: f (x, λ) = λe−λx I[x>0] , 则有 ∑n 2λnX ¯ = 2λ Xi ∼ χ22n . i=1 Previous Next First Last Back Forward 21 

24 .证: 首先证明 2λX1 ∼ χ22 . 因为 ( ∫ y y ) 2λ F (y) = P (2λX1 < y) = P X1 < = λe−λx dx, 2λ 0 所以 { y 1 −2 ′ 2 e 当y>0 f (y) = F (y) = 0 当y ≤ 0. 因此 f (y) 即为自由度为 2 的 χ2 密度, 即 2λX1 ∼ χ22 . 再利用 χ2 分布的性质 (3), 2λXi ∼ χ22 , i = 1, 2, · · · , n; 又它们 ∑ n 相互独立, 故有 2λ Xi ∼ χ22n . i=1 Previous Next First Last Back Forward 22 

25 . 4.2 总结 数据在使用前要注意采用有效的方法收集数据, 如设计好抽样方 案, 安排好试验等等. 只有有效的收集了数据, 才能有效地使用数据, 开展统计推断工作. 获得数据后, 根据问题的特点和抽样方式确定抽样分布, 即统计 模型. 基于统计模型, 统计推断问题可以按照如下的步骤进行: 1. 确定用于统计推断的合适统计量; 2. 寻求统计量的精确分布; 在统计量的精确分布难以求出的情形, 可考虑利用中心极限定理或其它极限定理找出统计量的极限分 布. 3. 基于该统计量的精确分布或极限分布, 求出统计推断问题的精 确解或近似解. 4. 根据统计推断结果对问题作出解释. Previous Next First Last Back Forward 23 

26 . 其中第二步是最重要, 但也是最困难的一步. 统计三大分布及正 态总体下样本均值和样本方差的分布, 在寻求与正态变量有关的统计 量精确分布时, 起着十分重要作用. 尤其在后面两章中求区间估计和 假设检验问题时可以看得十分清楚. Previous Next First Last Back Forward 24