展开查看详情
1 .Relations Between S ets 2/13/12 1
2 .Relations 2/13/12 2 Sam Mary CS20 EC 10 Students Courses The “is-taking” relation A relation is a set of ordered pairs: {(Sam,Ec10), (Sam, CS20), (Mary, CS20)}
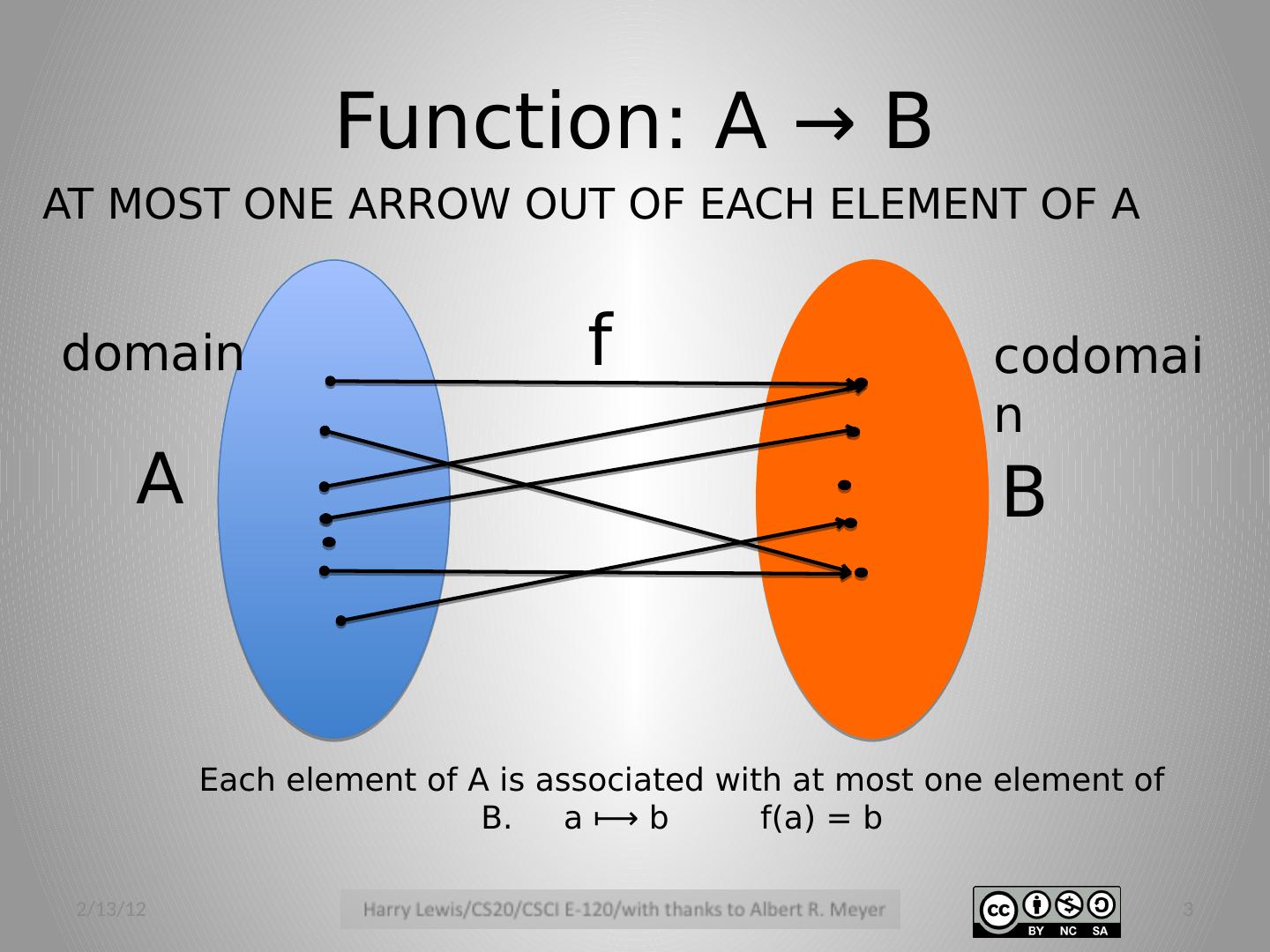
3 .Function: A → B 2/13/12 3 A B Each element of A is associated with at most one element of B. a ⟼ b f(a ) = b f AT MOST ONE ARROW OUT OF EACH ELEMENT OF A domain codomain
4 .Total Function: A → B 2/13/12 4 A B Each element of A is associated with ONE AND ONLY one element of B. a ⟼ b f(a ) = b f EXACTLY ONE ARROW OUT OF EACH ELEMENT OF A domain codomain
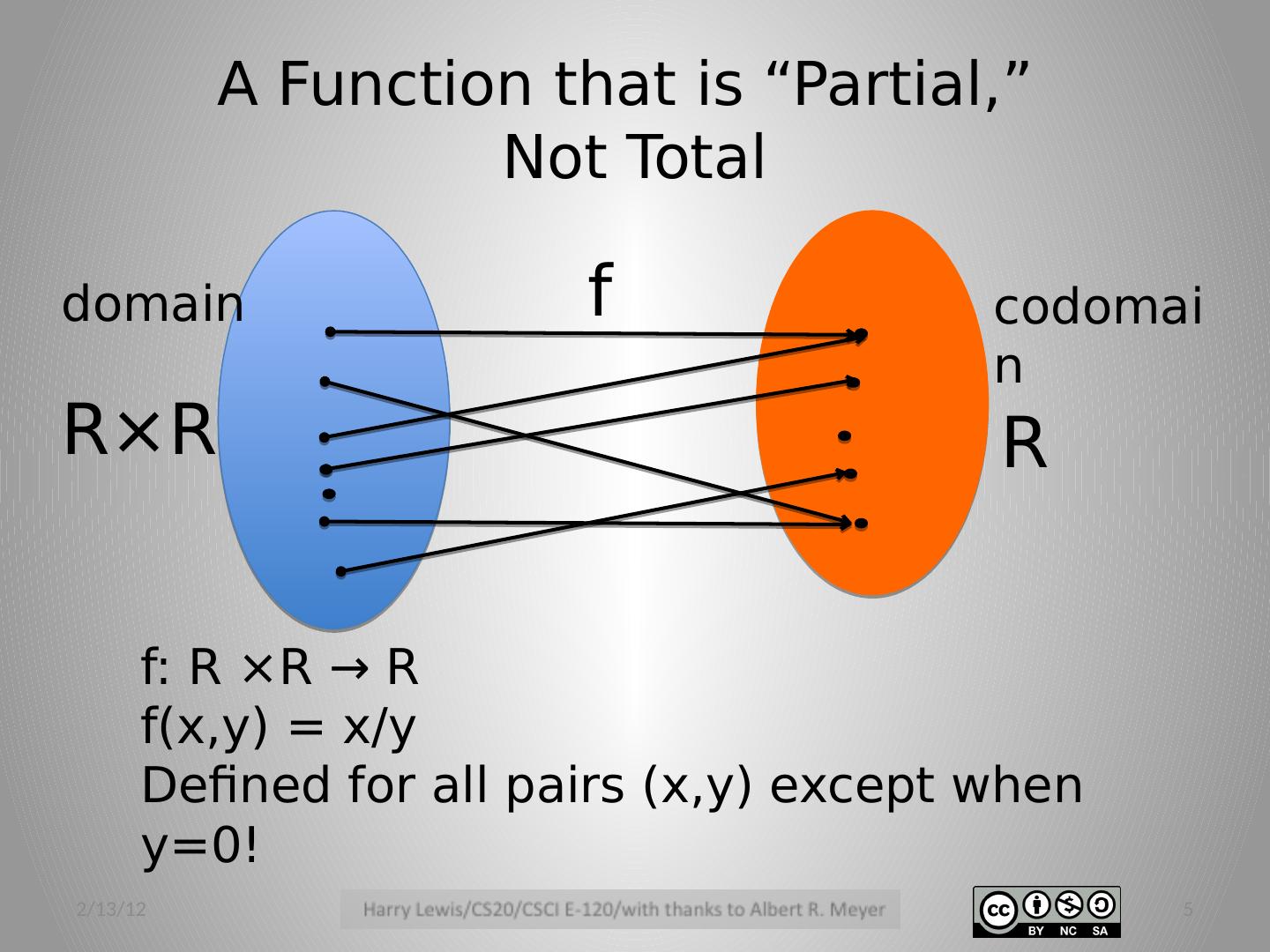
5 .A Function that is “Partial,” Not Total 2/13/12 5 R×R R f : R ×R → R f (x,y ) = x/y Defined for all pairs ( x,y ) except when y =0! f domain codomain
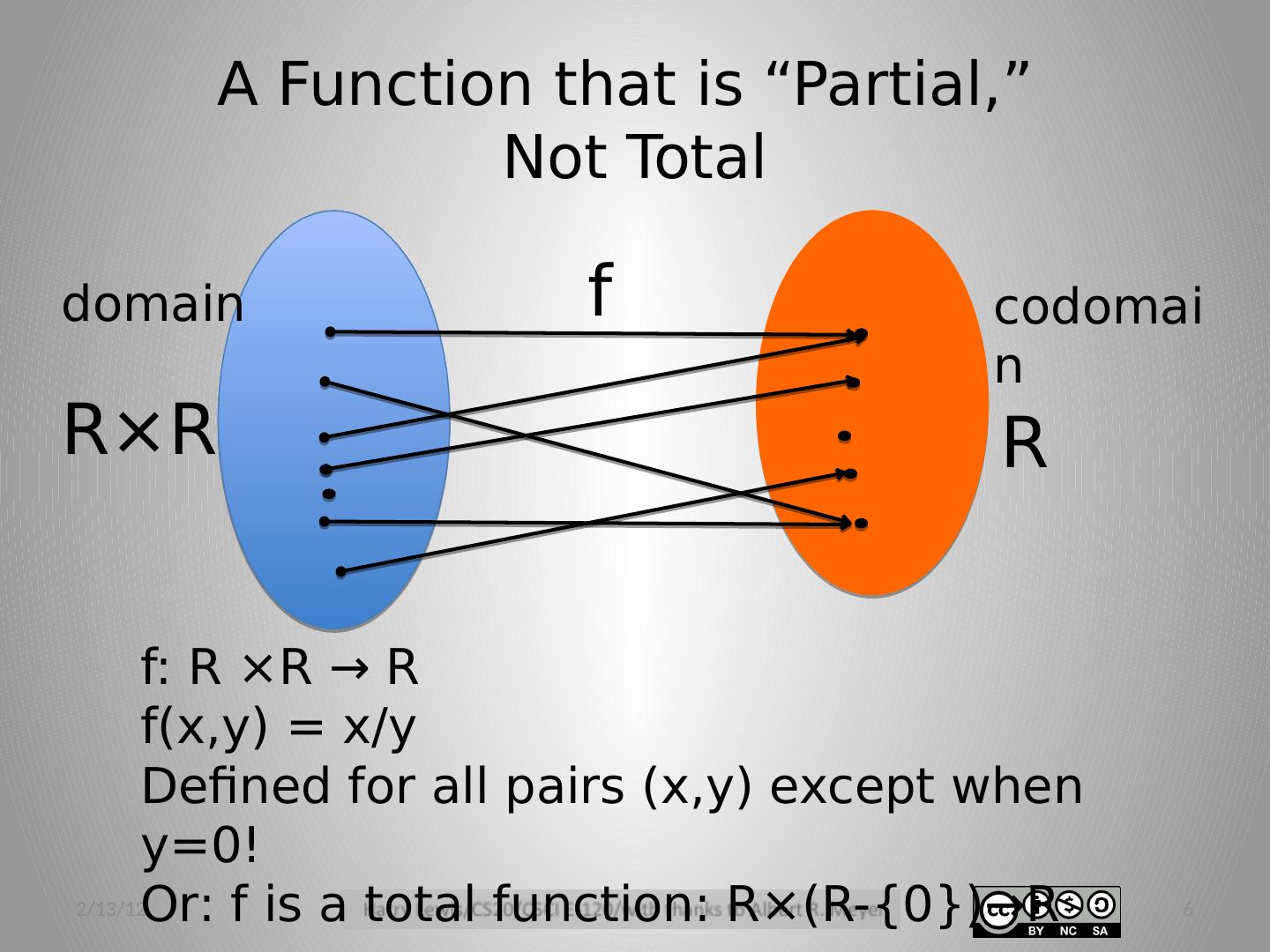
6 .A Function that is “Partial,” Not Total 2/13/12 6 R×R R f : R ×R → R f (x,y ) = x/y Defined for all pairs ( x,y ) except when y =0! Or: f is a total function: R×(R-{0})→R f domain codomain
7 .Injective Function 2/13/12 7 A B f domain codomain “at most one arrow in” (∀b∈B)(∃ ≤1 a∈A) f(a )= b
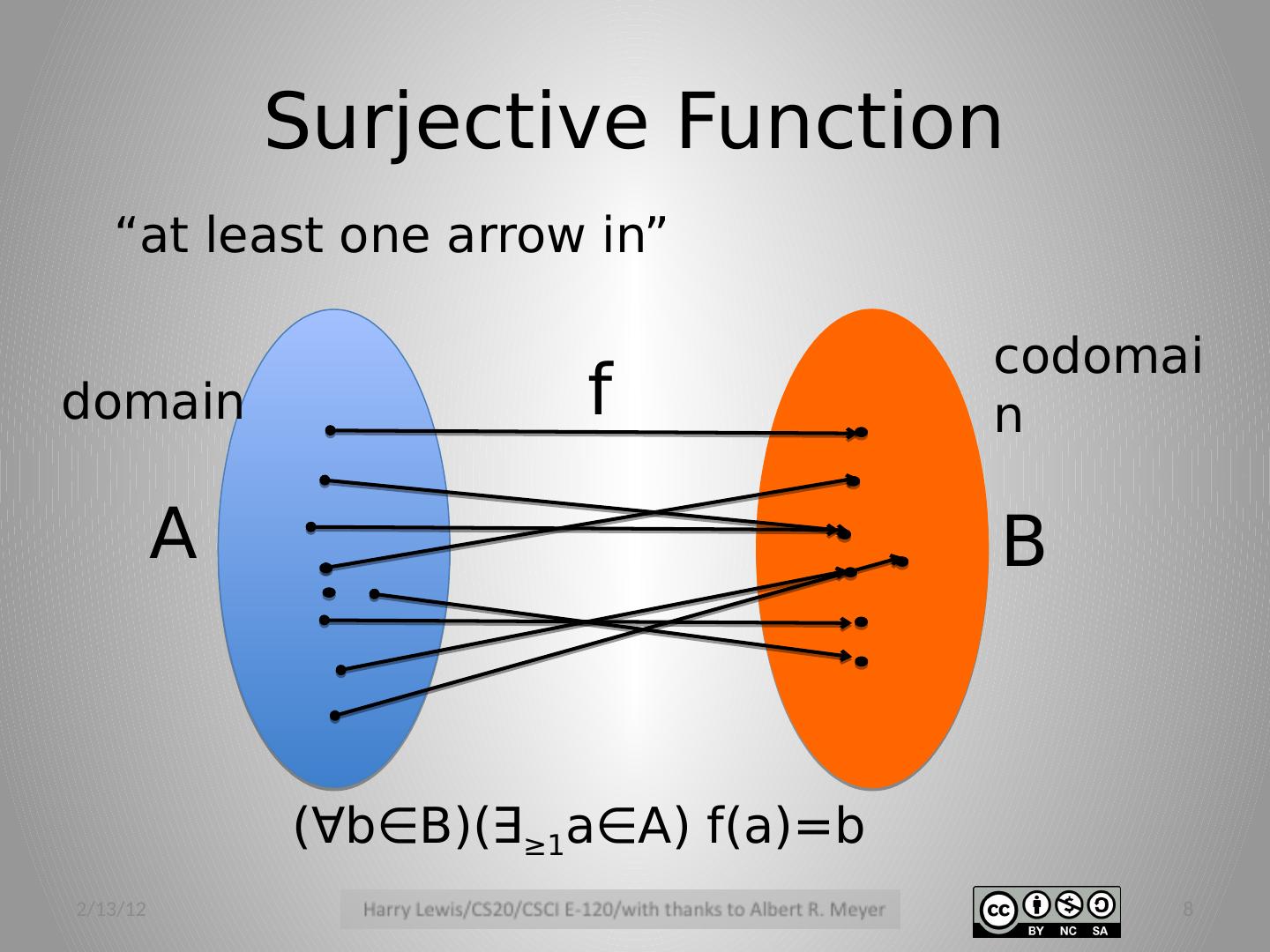
8 .Surjective Function 2/13/12 8 A B f domain codomain “at least one arrow in” (∀b∈B)(∃ ≥1 a∈A) f(a )= b
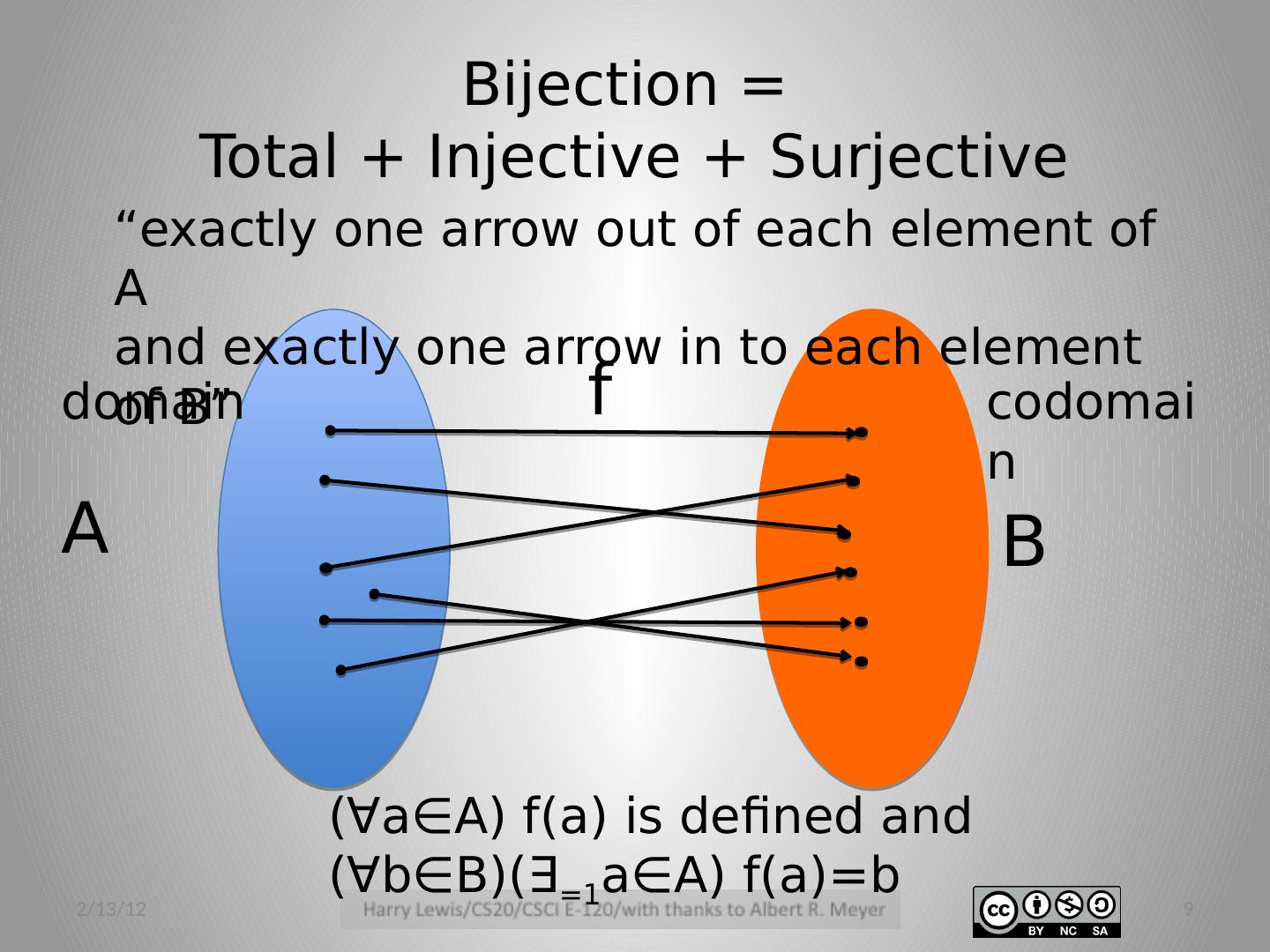
9 .Bijection = Total + Injective + Surjective 2/13/12 9 A B f domain codomain “exactly one arrow out of each element of A a nd exactly one arrow in to each element of B” ( ∀ a∈A ) f(a ) is defined and ( ∀ b∈B )(∃ =1 a∈A) f(a )= b
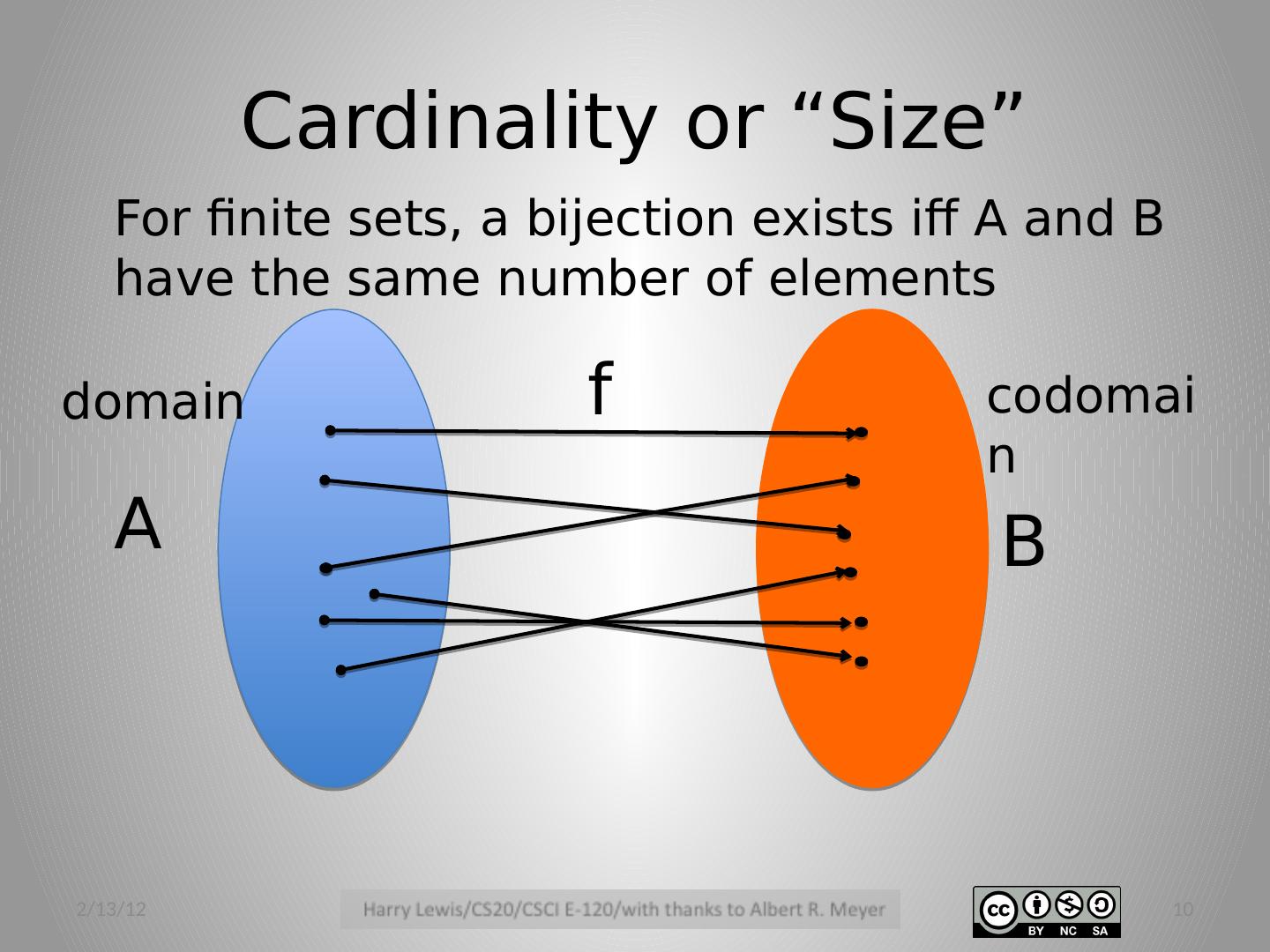
10 .Cardinality or “Size” 2/13/12 10 A B f domain codomain For finite sets, a bijection exists iff A and B have the same number of elements
11 .Cardinality or “Size” 2/13/12 11 Use the same as a definition of “same size” for infinite sets: Sets A and B have the same size iff there is a bijection between A and B Theorem: The set of even integers has the same size as the set of all integers [f(2n) = n ] …, -4, -3, -2, -1, 0, 1, 2, 3, 4 … …, -8, -6, -4, -2, 0, 2, 4, 6, 8 …
12 .Cardinality or “Size” 2/13/12 12 There are as many natural numbers as integers 0 1 2 3 4 5 6 7 8 … 0, -1, 1, -2, 2, -3, 3, -4, 4 … f(n ) = n/2 if n is even, -(n+1)/2 if n is odd Defn : A set is countably infinite if it has the same size as the set of natural numbers
13 .An Infinite Set May Have the Same Size as a Proper Subset! 2/13/12 13 0 1 2 3 4 5 0 1 2 3 4 5 Hilton Sheraton Every room of both hotels is full! Suppose the Sheraton has to be evacuated ⋮ ⋮
14 .An Infinite Set May Have the Same Size as a Proper Subset! 2/13/12 14 0 1 2 3 4 5 0 1 2 3 4 5 Hilton Sheraton Step 1: Tell the resident of room n in the Hilton to go to room 2n This leaves all the odd-numbered rooms of the Hilton unoccupied ⋮ ⋮
15 .An Infinite Set May Have the Same Size as a Proper Subset! 2/13/12 15 0 1 2 3 4 5 0 1 2 3 4 5 Hilton Sheraton Step 2: Tell the resident of room n in the Sheraton to go to room 2n+1 of the Hilton. Everyone gets a room! ⋮ ⋮
热门城市
