- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
逻辑与运算
展开查看详情
1 . Logic and computers 2/6/12
2 . Binary Arithmetic Only two digits: the bits 0 and 1 (Think: 0 = F, 1 = T) 0 0 1 1 +0 +1 +0 +1 ---- ---- ---- ---- 0 1 1 10 2/6/12
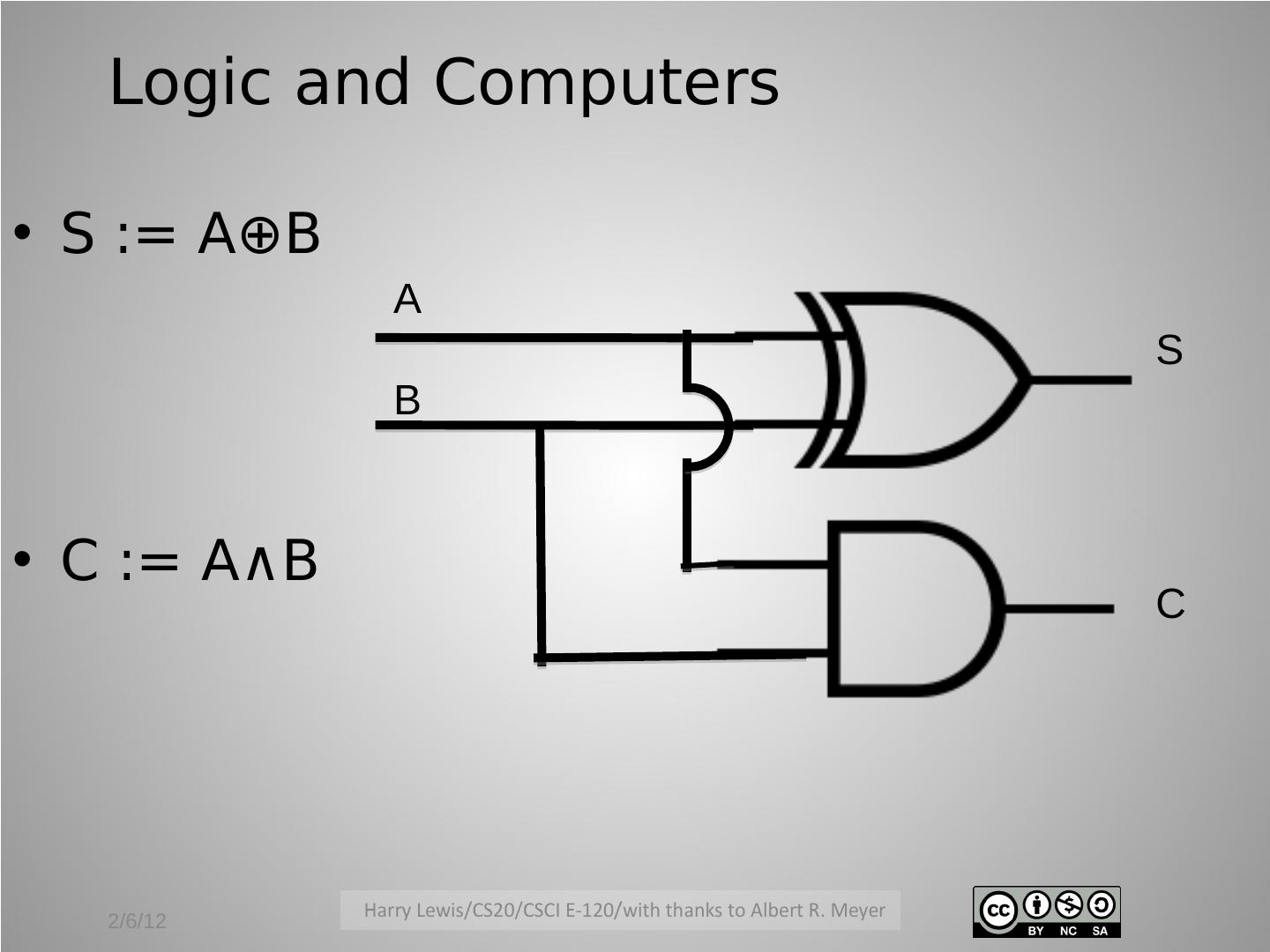
3 .Logic and Computers A half adder: Two bits in (A, B: to be added together) Two bits out (S, C: sum and carry) 0+0=0, carry 0 0+1=1, carry 0 1+0=1, carry 0 1+1=0, carry 1 S := A⊕B C := A∧B 2/6/12
4 . NOT OR NOR AND NAND XOR NXOR (EQUIV) 2/6/12
5 . Logic and Computers • S := A⊕B A S B • C := A∧B C 2/6/12
6 . Half Adder A S B HA C A S B C 2/6/12
7 . A Longer Addition 11 11 +11 110 2/6/12
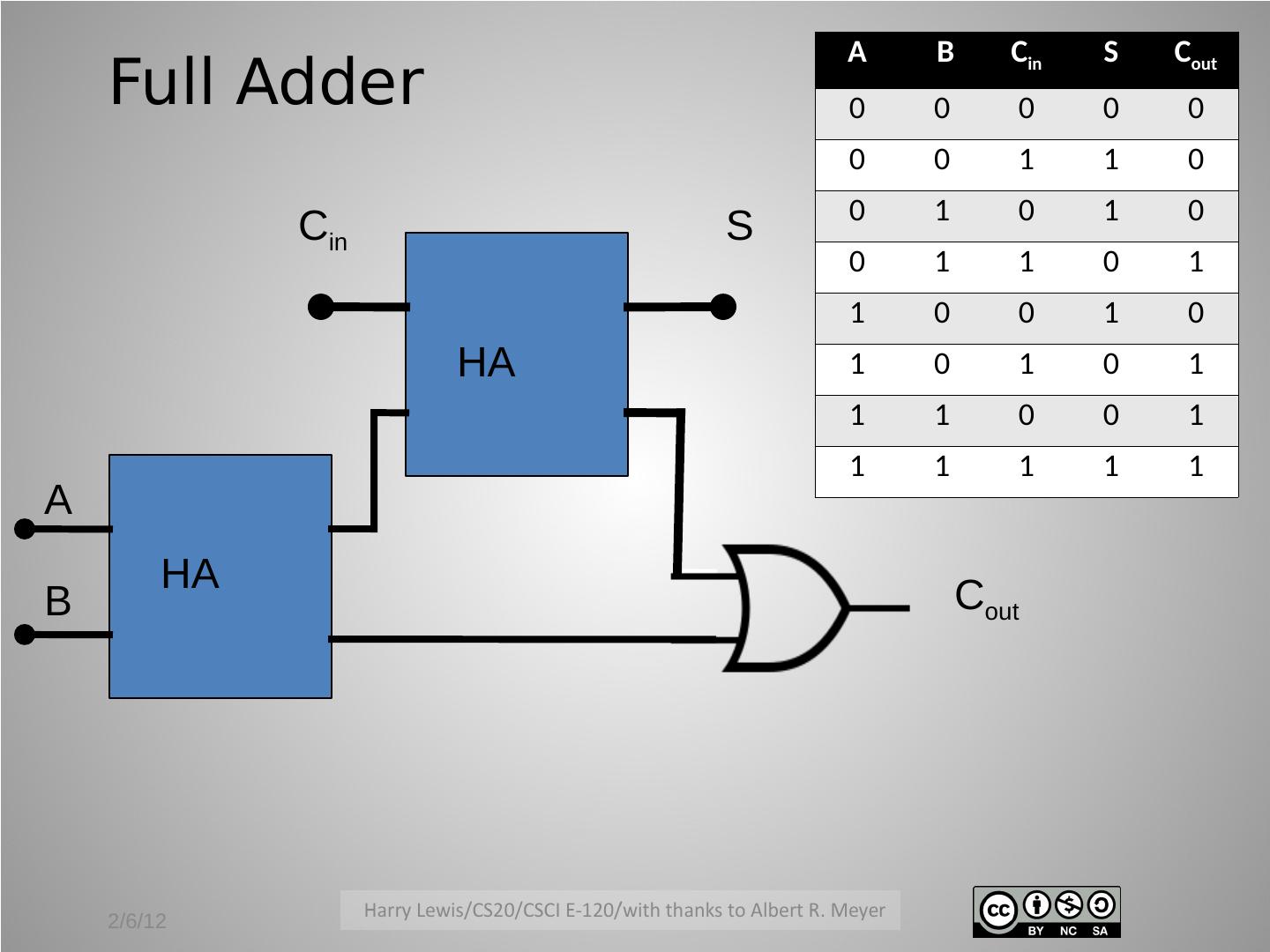
8 .Full Adder A B Cin S Cout • Need a third input to 0 0 0 0 0 create a component of 0 0 1 1 0 a ripple-carry adder: 0 1 0 1 0 0 1 1 0 1 the carry from the 1 0 0 1 0 previous bit position 1 0 1 0 1 1 1 0 0 1 • Inputs: A, B, Cin 1 1 1 1 1 • Outputs: S, Cout 2/6/12
9 . A B Cin S Cout Full Adder 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 Cin S 0 1 1 0 1 1 0 0 1 0 HA 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 A HA B Cout 2/6/12
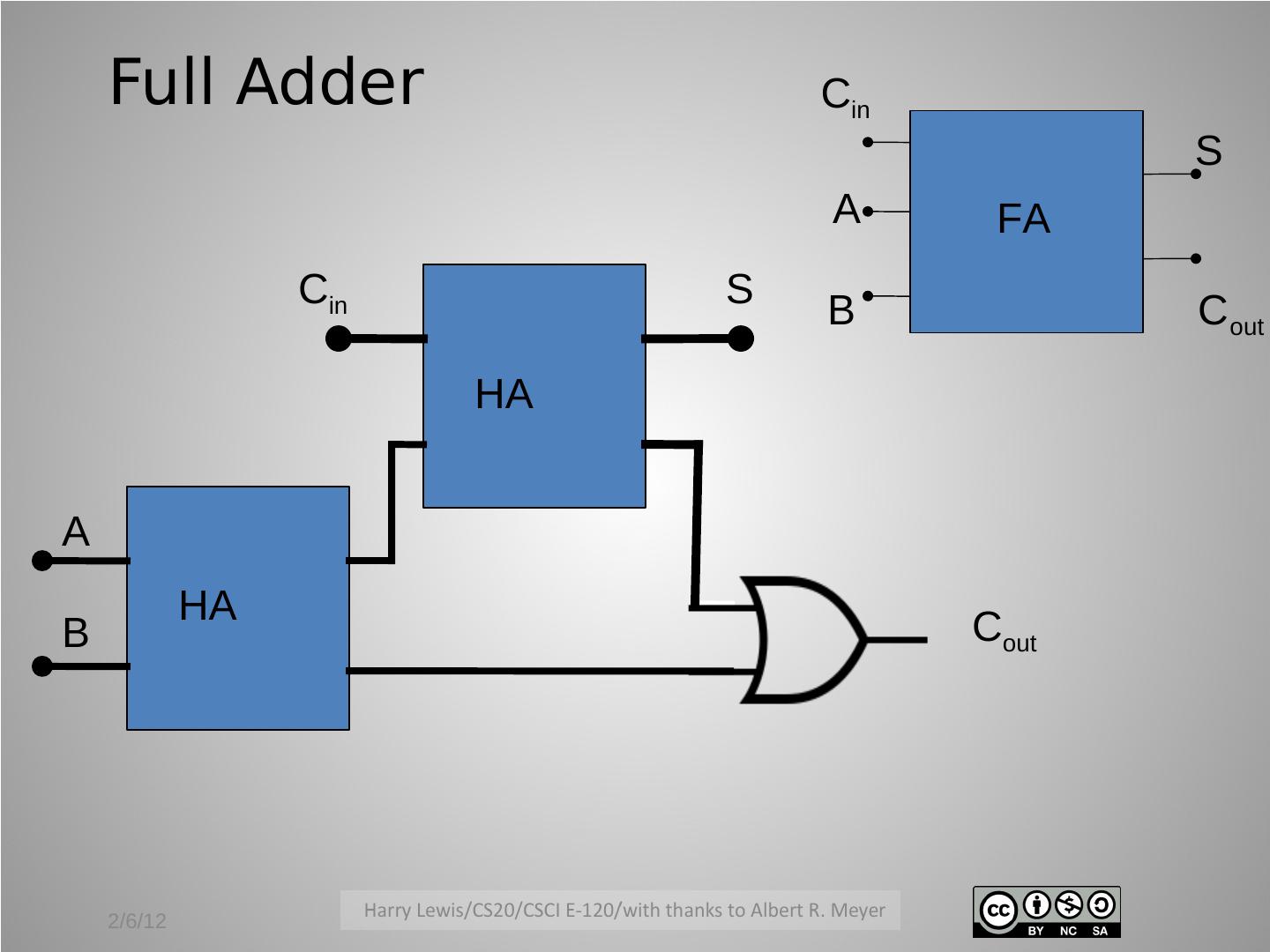
10 . Full Adder Cin S A FA Cin S B C out HA A HA B Cout 2/6/12
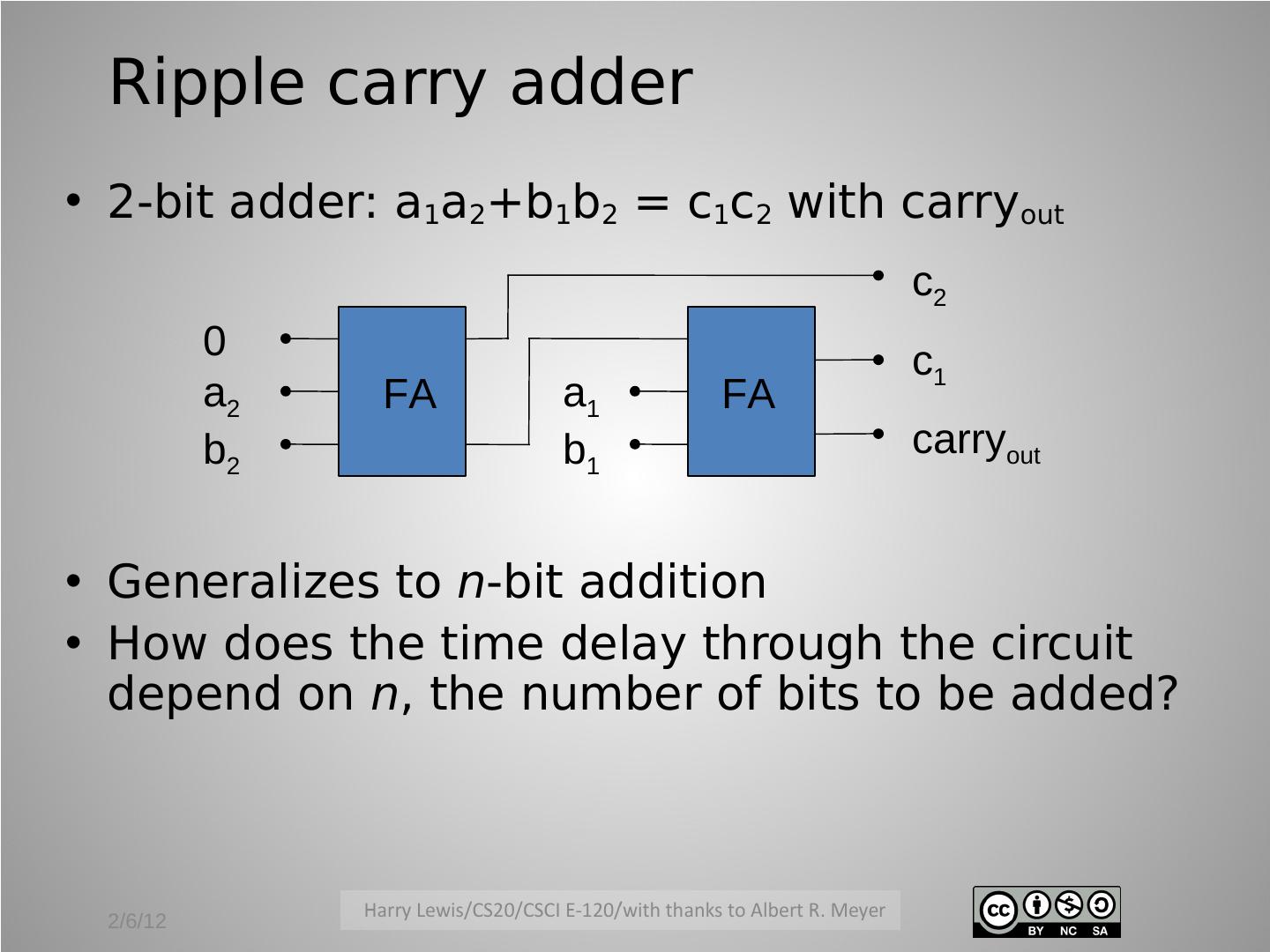
11 . Ripple carry adder • 2-bit adder: a1a2+b1b2 = c1c2 with carryout c2 0 c1 a2 FA a1 FA b2 b1 carryout • Generalizes to n-bit addition • How does the time delay through the circuit depend on n, the number of bits to be added? 2/6/12
12 . Simplifying Circuits • Simpler formulas turn into circuits that use less hardware! • E.g. p ⋁ q ⋁ (p⋀q) is equivalent to p ⋁ q but would use more logic gates • But the P=NP? question means that it may be hard to simplify formulas as much as possible – Any tautology is equivalent to p ⋁ ¬p so if we could easily simplify formulas we could easily determine whether a formula is a tautology 2/6/12