数字逻辑结构

1 .Chapter 3 Digital Logic Structures

2 .3- 2 Transistor: Building Block of Computers Microprocessors contain millions of transistors Intel Pentium II: 7 million Compaq Alpha 21264: 15 million Intel Pentium III: 28 million Intel Pentium4: 55 Million Intel Core 2 Duo: 291 Million Logically, each transistor acts as a switch Combined to implement logic functions AND, OR, NOT Combined to build higher-level structures Adder, multiplexor, decoder, register, … Combined to build processor LC-3

3 .Transistors 3- 3 First transistor: Bell Labs in 1947; developed by J. Bardeen, W. Shockley & W. Brattain A 2011 processor with 1.17 billion transistors positioned in 240 sq. millimeters http ://www.brew-wood.co.uk/computers/transistor.htm

4 .3- 4 Simple Switch Circuit Switch open : No current through circuit Light is off V out is +2.9V Switch closed : Short circuit across switch Current flows Light is on V out is 0V Switch-based circuits can easily represent two states: on/off, open/closed, voltage/no voltage.

5 .3- 5 N-type MOS Transistor MOS = Metal Oxide Semiconductor two types: N-type and P-type N-type when Gate has positive voltage, short circuit between #1 and #2 (switch closed ) when Gate has zero voltage, open circuit between #1 and #2 (switch open ) Gate = 1 Gate = 0 Terminal #2 must be connected to GND (0V). Animation D rain Source GND GND

6 .3- 6 P-type MOS Transistor P-type is complementary to N-type when Gate has positive voltage, open circuit between #1 and #2 (switch open ) when Gate has zero voltage, short circuit between #1 and #2 (switch closed ) Gate = 1 Gate = 0 Terminal #1 must be connected to +2.9V. Source D rain GND +2.9V

7 .3- 7 CMOS Circuit Complementary MOS Uses both N-type and P-type MOS transistors P-type Attached to + voltage Pulls output voltage UP when input is zero N-type Attached to GND Pulls output voltage DOWN when input is one For all inputs, make sure that output is either connected to GND or to +, but not both!

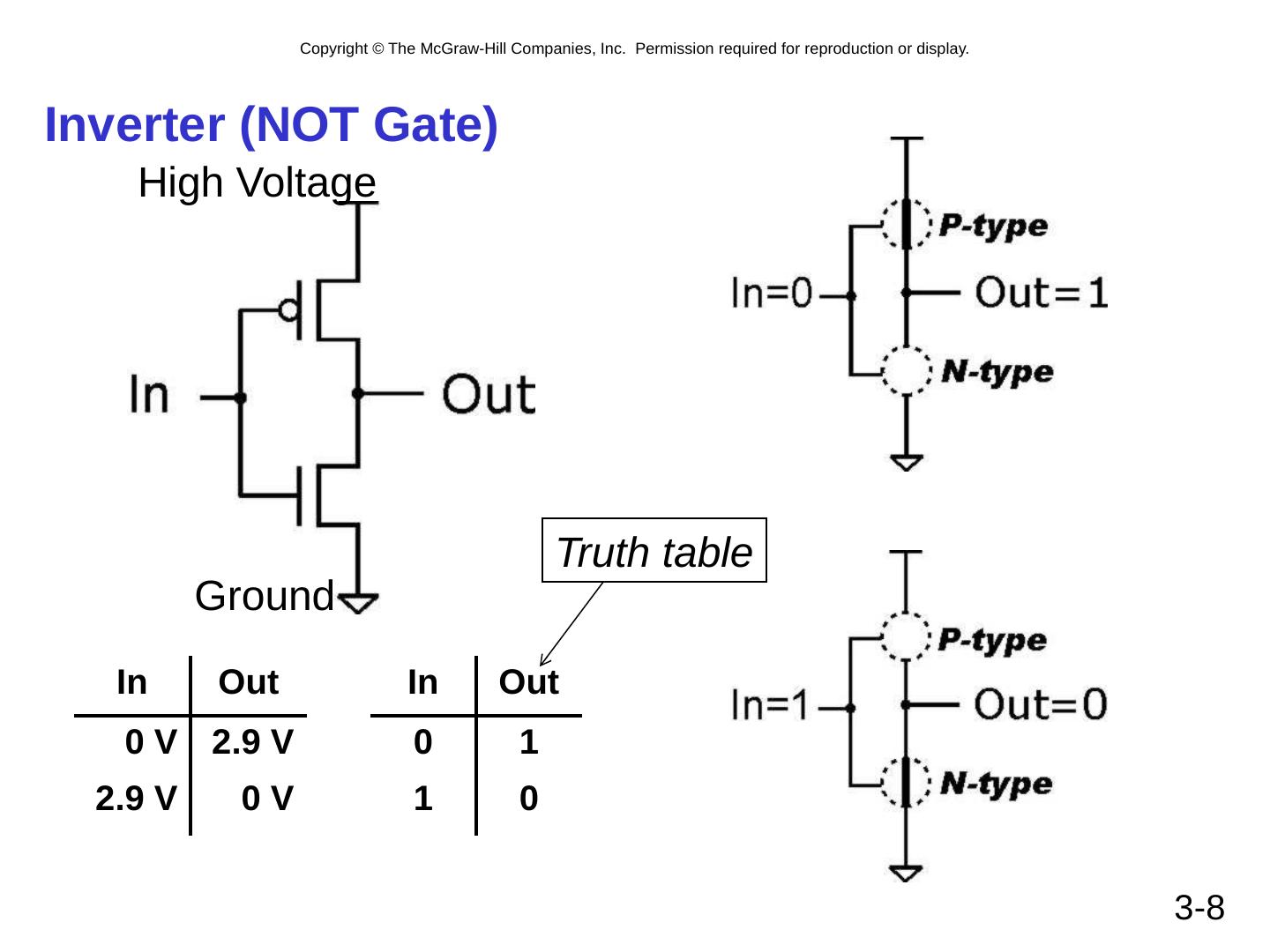
8 .3- 8 Inverter (NOT Gate) In Out 0 V 2.9 V 2.9 V 0 V In Out 0 1 1 0 Truth table High Voltage Ground

9 .Logical Operations In 1850, George Boole developed Boolean Algebra showing that all logical functions can be performed with just 3 operations (AND, OR & NOT). In 1937, Claude Shannon showed that Boolean Algebra could be applied to circuit design. 3- 9 http://www.computerhistory.org/revolution/digital-logic/12/269

10 .3- 10 NOR Gate (NOT OR) A B C 0 0 1 0 1 0 1 0 0 1 1 0 Note: Serial structure on top, parallel on bottom. High Voltage Ground

11 .3- 11 OR Gate Add inverter to NOR. A B C 0 0 0 0 1 1 1 0 1 1 1 1

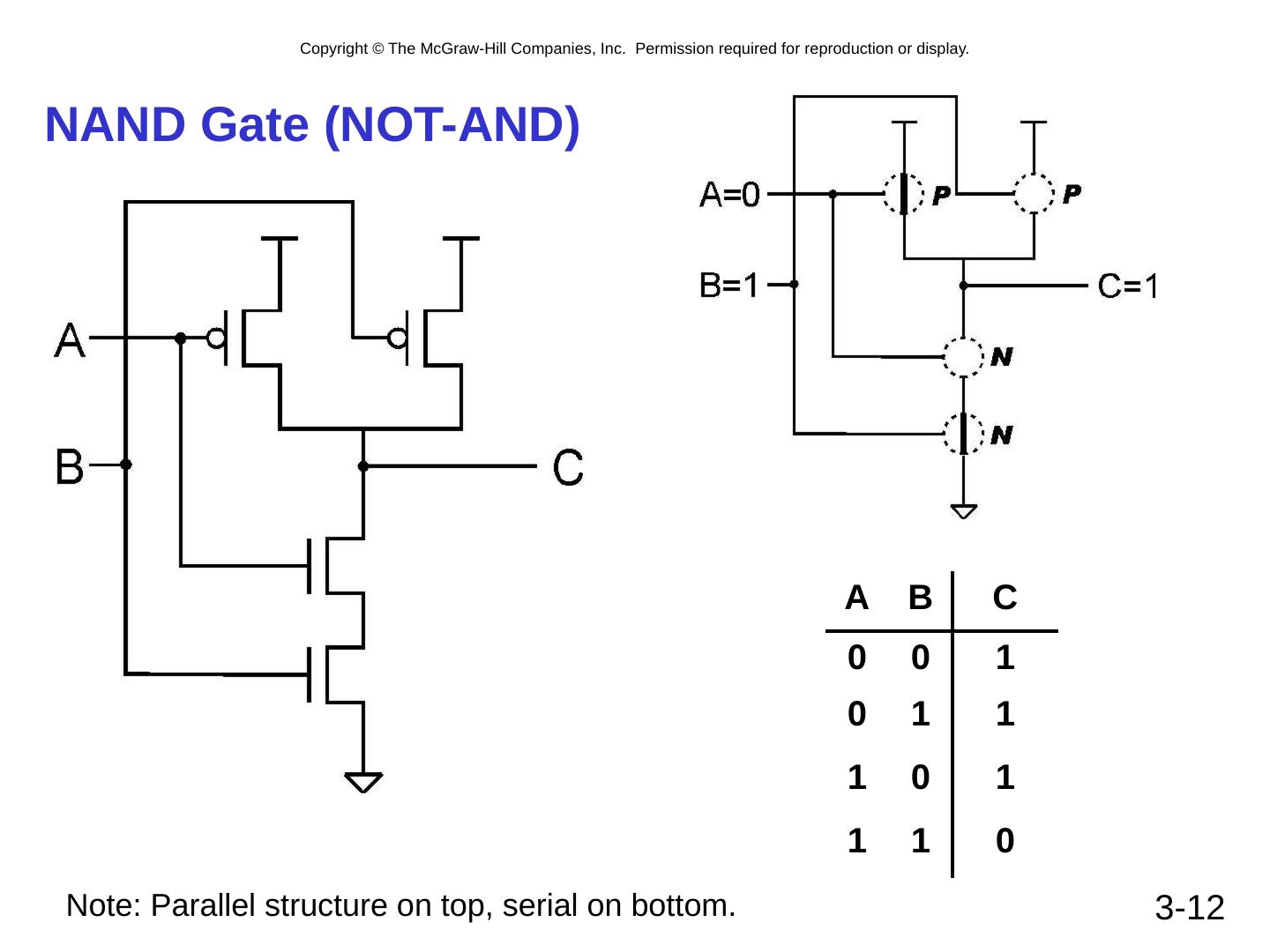
12 .3- 12 NAND Gate (NOT-AND) A B C 0 0 1 0 1 1 1 0 1 1 1 0 Note: Parallel structure on top, serial on bottom.

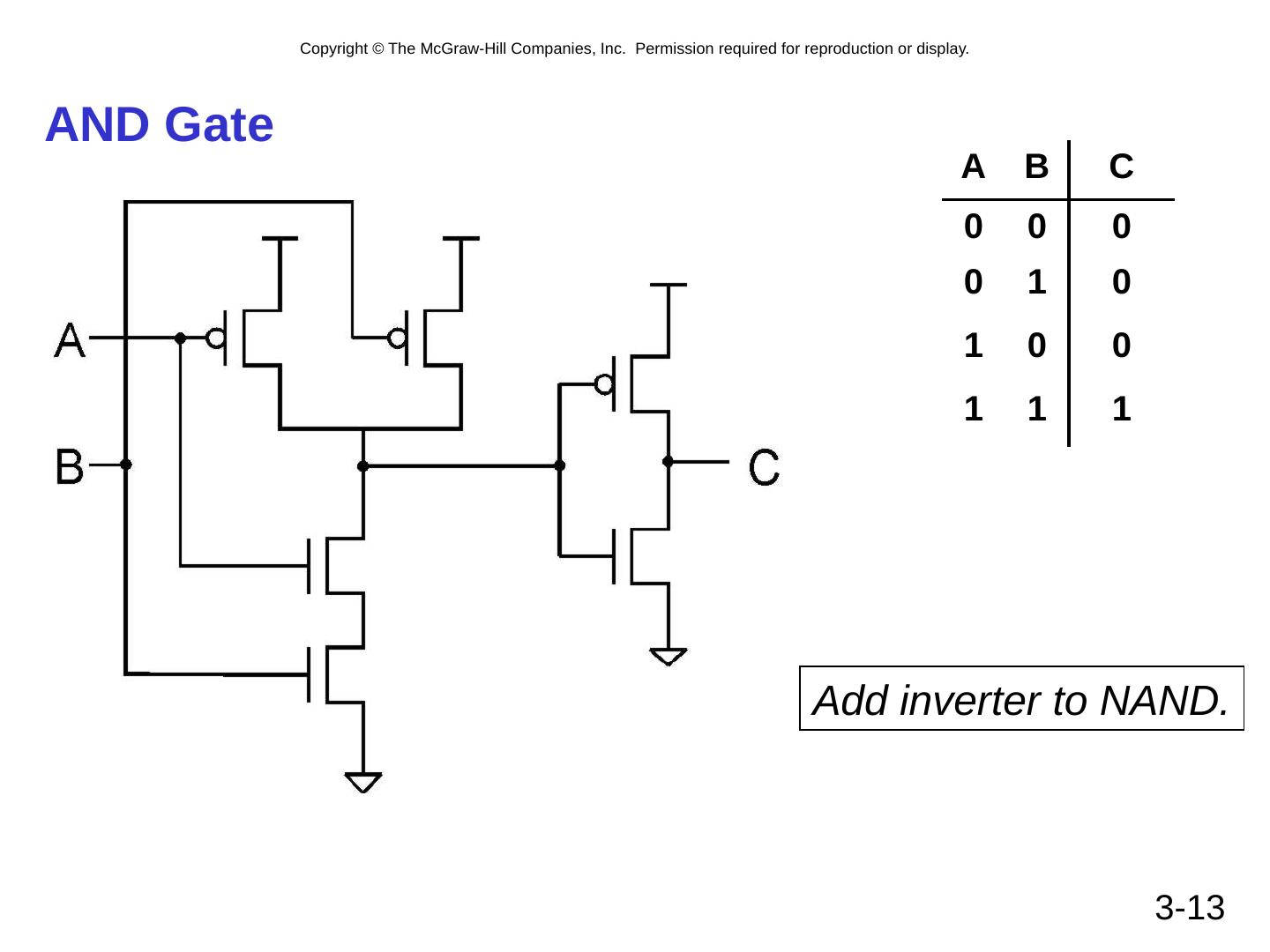
13 .3- 13 AND Gate Add inverter to NAND. A B C 0 0 0 0 1 0 1 0 0 1 1 1

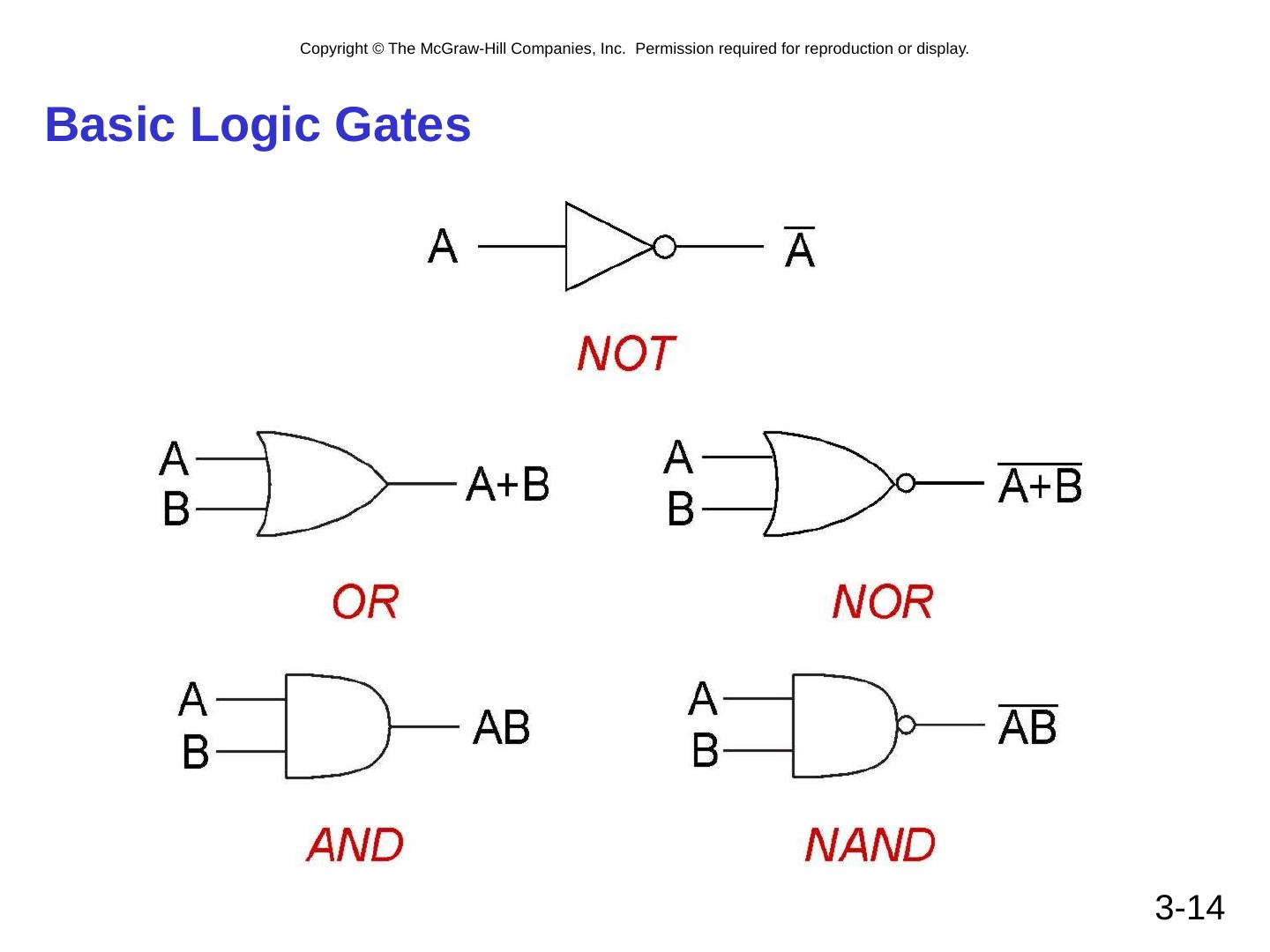
14 .3- 14 Basic Logic Gates

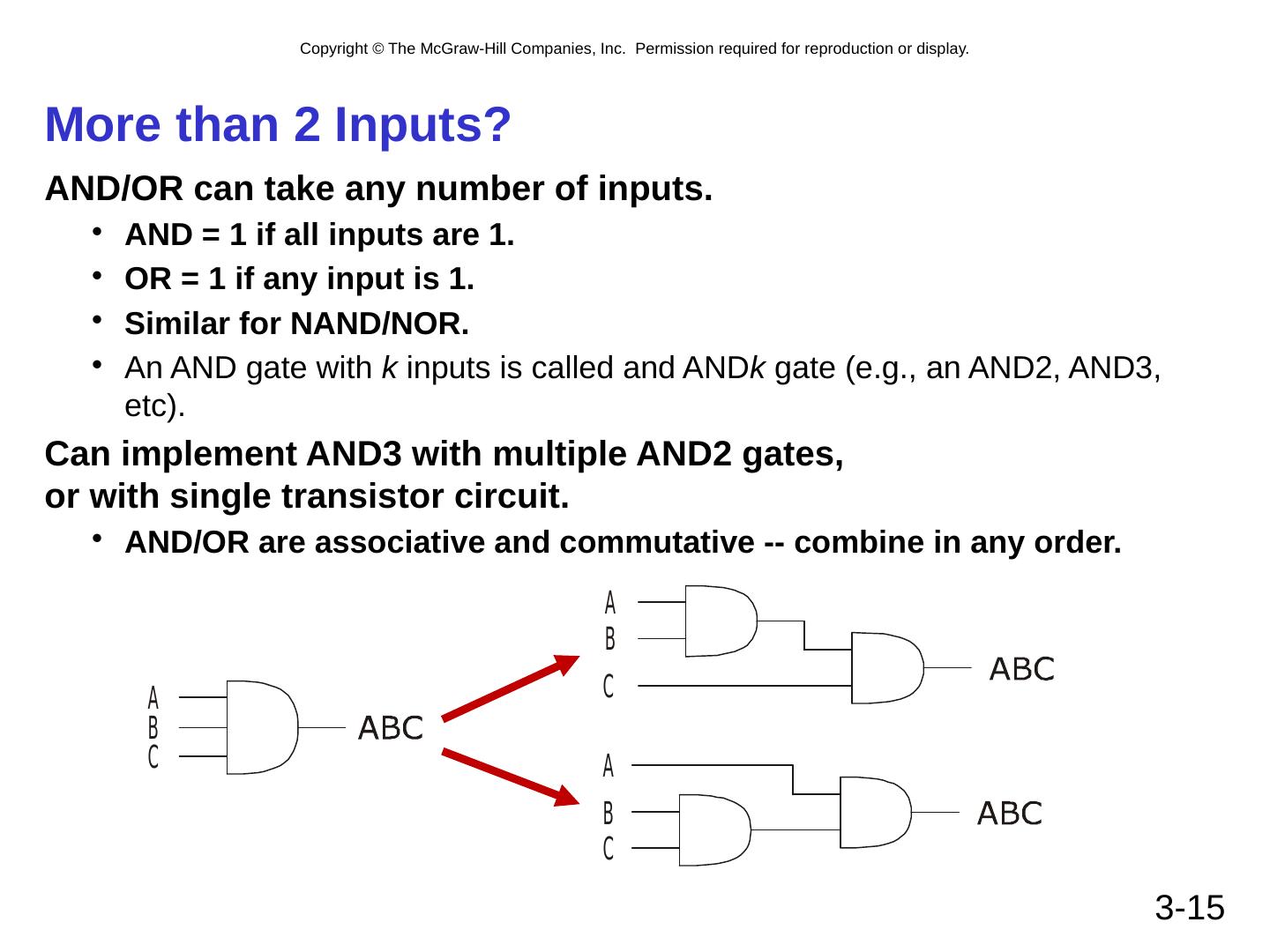
15 .3- 15 More than 2 Inputs? AND/OR can take any number of inputs. AND = 1 if all inputs are 1. OR = 1 if any input is 1. Similar for NAND/NOR. An AND gate with k inputs is called and AND k gate (e.g., an AND2, AND3, etc). Can implement AND3 with multiple AND2 gates, or with single transistor circuit. AND/OR are associative and commutative -- combine in any order.

16 .3- 16 Logical Completeness Can implement ANY truth table with AND, OR, NOT. A B C D 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 0 AND combinations that yield a "1" in the truth table. Put a “bubble” (inverter) for every 0, a straight-in for every 1 in a row 2. OR the results of the AND gates. If there are N 1’s, there will be N and gates; the or gate will have N inputs

17 .3- 16 Logical Completeness Can implement ANY truth table with AND, OR, NOT. A B C D 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 0 AND combinations that yield a "1" in the truth table. Put a “bubble” (inverter) for every 0, a straight-in for every 1 in a row 2. OR the results of the AND gates. If there are N 1’s, there will be N and gates; the or gate will have N inputs

18 .3- 16 Logical Completeness Can implement ANY truth table with AND, OR, NOT. A B C D 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 0 AND combinations that yield a "1" in the truth table. Put a “bubble” (inverter) for every 0, a straight-in for every 1 in a row 2. OR the results of the AND gates. If there are N 1’s, there will be N and gates; the or gate will have N inputs