Divide, Floating Point, Pentium Bug

1 . ECE4680 Computer Organization & Architecture Divide, Floating Point, Pentium Bug ECE468 ALU-III.1 2002-2-27 Review: MULTIPLY HARDWARE Version 1 °64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg, 32-bit multiplier reg Multiplicand Shift Left 64 bits Multiplier Shift Right 64-bit ALU 32 bits Product Write Control 64 bits ECE468 ALU-III.2 2002-2-27 

2 . Review: MULTIPLY HARDWARE Version 3 °32-bit Multiplicand reg, 32 -bit ALU, 64-bit Product reg, (0-bit Multiplier reg) Multiplicand 32 bits 32-bit ALU Product Shift Right Write Control 64 bits ECE468 ALU-III.3 2002-2-27 Review: Booth’s Algorithm Insight middle of run end of run beginning of run 0 1 1 1 1 0 Current Bit Bit to the Right Explanation Example 1 0 Beginning of a run of 1s 0001111000 1 1 Middle of a run of 1s 0001111000 0 1 End of a run of 1s 0001111000 0 0 Middle of a run of 0s 0001111000 Originally for Speed since shift faster than add for his machine ECE468 ALU-III.4 2002-2-27 

3 . Review: Booth’s Algorithm 1. Depending on the current and previous bits, do one of the following: 00: a. Middle of a string of 0s, so no arithmetic operations. 01: b. End of a string of 1s, so add the multiplicand to the left half of the product. 10: c. Beginning of a string of 1s, so subtract the multiplicand from the left half of the product. 11: d. Middle of a string of 1s, so no arithmetic operation. 2.As in the previous algorithm, shift the Product register right (arith) 1 bit. Multiplicand Product (2 x 3) Multiplicand Product (2 x -3) 0010 0000 0011 0 0010 0000 1101 0 ECE468 ALU-III.5 2002-2-27 Divide: Paper & Pencil 1001 Quotient Divisor 1000 1001010 Dividend –1000 10 101 1010 –1000 10 Remainder °See how big a number can be subtracted, creating quotient bit on each step • Binary => 1 * divisor or 0 * divisor °Dividend = Quotient x Divisor + Remainder °3 versions of divide, successive refinement ECE468 ALU-III.6 2002-2-27 

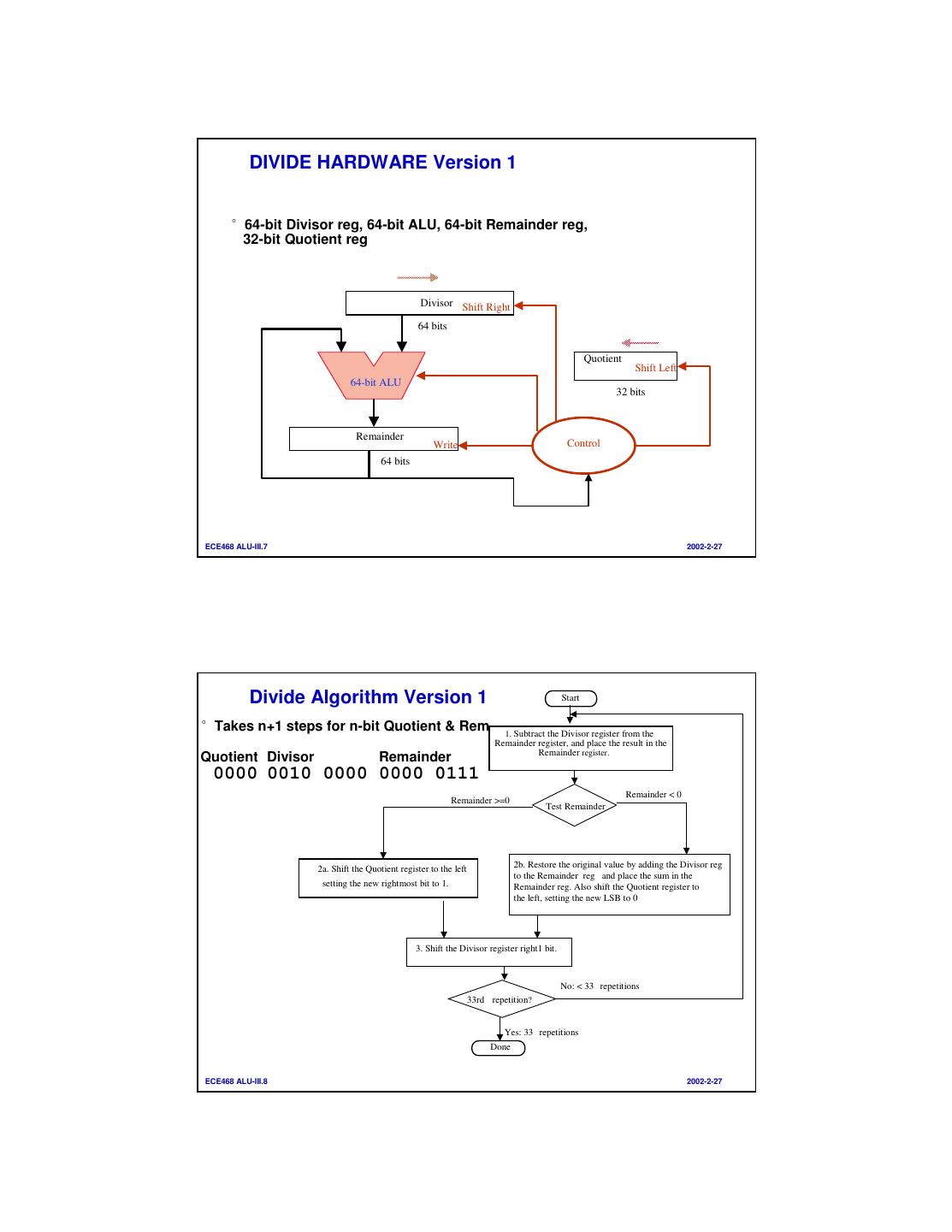
4 . DIVIDE HARDWARE Version 1 °64-bit Divisor reg, 64-bit ALU, 64-bit Remainder reg, 32-bit Quotient reg Divisor Shift Right 64 bits Quotient Shift Left 64-bit ALU 32 bits Remainder Write Control 64 bits ECE468 ALU-III.7 2002-2-27 Divide Algorithm Version 1 Start °Takes n+1 steps for n-bit Quotient & Rem 1. Subtract the Divisor register from the Remainder register, and place the result in the Remainder register. Quotient Divisor Remainder 0000 0010 0000 0000 0111 Remainder < 0 Remainder >=0 Test Remainder 2b. Restore the original value by adding the Divisor reg 2a. Shift the Quotient register to the left to the Remainder reg and place the sum in the setting the new rightmost bit to 1. Remainder reg. Also shift the Quotient register to the left, setting the new LSB to 0 3. Shift the Divisor register right1 bit. No: < 33 repetitions 33rd repetition? Yes: 33 repetitions Done ECE468 ALU-III.8 2002-2-27 

5 . Observations on Divide Version 1 °1/2 bits in divisor always 0 => 1/2 of 64-bit adder is wasted => 1/2 of divisor is wasted °Instead of shifting divisor to right, shift remainder to left? °1st step cannot produce a 1 in quotient bit ( otherwise too big) => switch order to shift first and then subtract, can save 1 iteration ECE468 ALU-III.9 2002-2-27 DIVIDE HARDWARE Version 2 °32-bit Divisor reg, 32 -bit ALU, 64-bit Remainder reg, 32-bit Quotient reg Divisor 32 bits Quotient 32-bit ALU Shift Left 32 bits Remainder Shift Left Write Control 64 bits ECE468 ALU-III.10 2002-2-27 

6 . Start Divide Algorithm Version 2 Quotient Divisor Remainder 1. Shift the Remainder register left 1 bit 0000 0010 0000 0111 2. Subtract the Divisor register from the left half of the Remainder register, and place the result in the left half of the Remainder register Remainder >=0 Remainder < 0 Test Remainder 3b. Restore the original value by adding the Divisor reg to the left half of the Remainder 3a. Shift the Quotient register . to the reg and place the sum in the left half of the Left setting the new rightmost bit to 1. Remainder reg. Also, shift the Quotient reg to the left, setting the new LSB to 0. No: < 32 repetitions 32nd repetition? Yes: 32 repetitions Done ECE468 ALU-III.11 2002-2-27 Observations on Divide Version 2 °Eliminate Quotient register by combining with Remainder as shifted left • Start by shifting the Remainder left as before. • Thereafter loop contains only two steps because the shifting of the Remainder register shifts both the remainder in the left half and the quotient in the right half • The consequence of combining the two registers together and the new order of the operations in the loop is that the remainder will shifted left one time too many. • Thus the final correction step must shift back only the remainder in the left half of the register ECE468 ALU-III.12 2002-2-27 

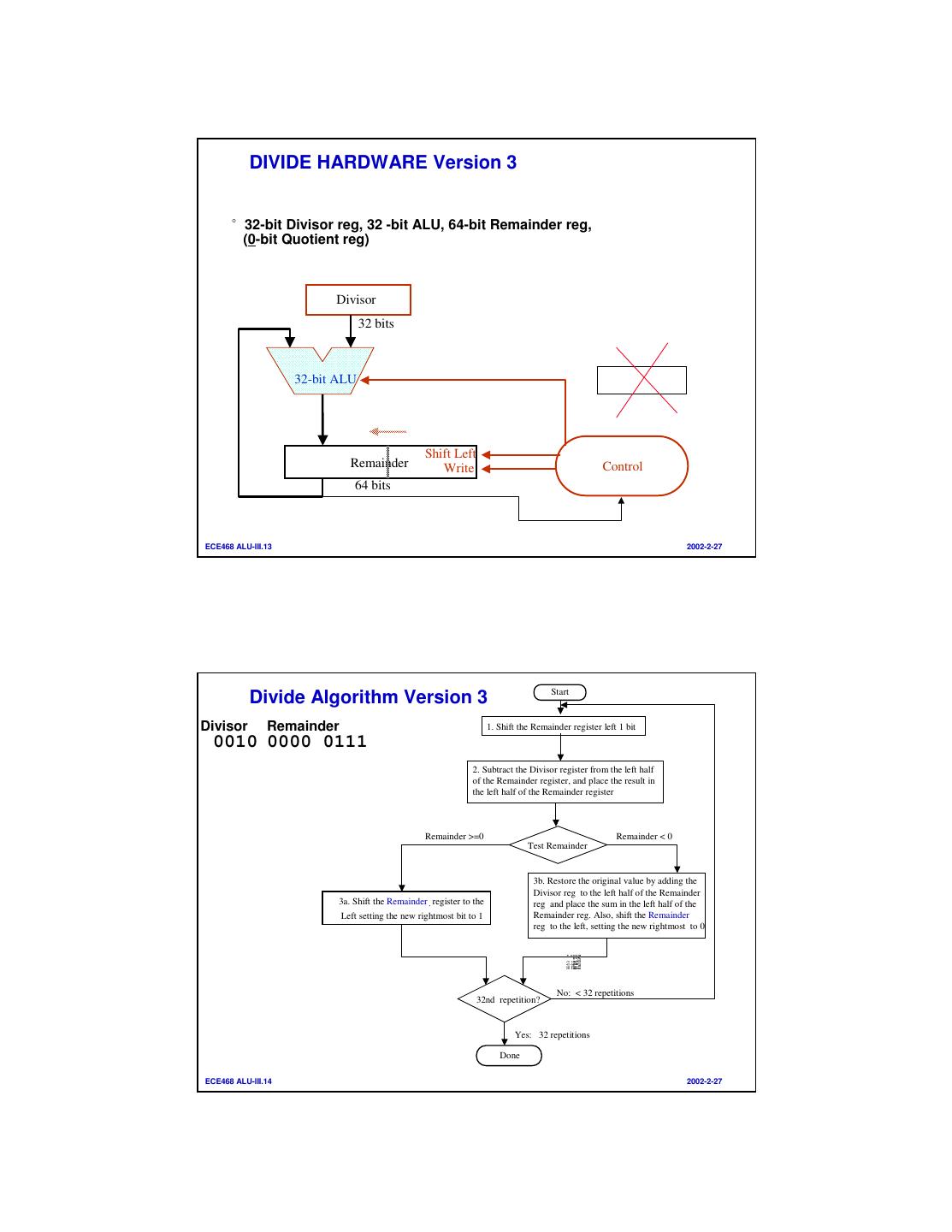
7 . DIVIDE HARDWARE Version 3 °32-bit Divisor reg, 32 -bit ALU, 64-bit Remainder reg, (0-bit Quotient reg) Divisor 32 bits 32-bit ALU Shift Left Remainder Write Control 64 bits ECE468 ALU-III.13 2002-2-27 Start Divide Algorithm Version 3 Divisor Remainder 1. Shift the Remainder register left 1 bit 0010 0000 0111 2. Subtract the Divisor register from the left half of the Remainder register, and place the result in the left half of the Remainder register Remainder >=0 Remainder < 0 Test Remainder 3b. Restore the original value by adding the Divisor reg to the left half of the Remainder 3a. Shift the Remainder . register to the reg and place the sum in the left half of the Left setting the new rightmost bit to 1 Remainder reg. Also, shift the Remainder reg to the left, setting the new rightmost to 0 No: < 32 repetitions 32nd repetition? Yes: 32 repetitions Done ECE468 ALU-III.14 2002-2-27 

8 . Observations on Divide Version 3 °Same Hardware as Multiply: just need ALU to add or subtract, and 63- bit register to shift left or shift right °Hi and Lo registers in MIPS combine to act as 64-bit register for multiply and divide °Signed Divides: Simplest is to remember signs, make positive, and complement quotient and remainder if necessary • Note: Dividend and Remainder must have same sign (Uniqueness) • Note: Quotient negated if Divisor sign & Dividend sign disagree ECE468 ALU-III.15 2002-2-27 Floating-Point °What can be represented in N bits? N • Unsigned 0 to 2 -1 N-1 N-1 • 2s Complement -2 to 2 -1 N-1 N-1 • 1s Complement -2 + 1 to 2 -1 N • Excess M -M to 2-M-1 (E = e + M) also called biased notation N/4 • BCD 0 to 10 - 1 °But, what about? • very large numbers? 9,349,398,989,787,762,244,859,087,678 • very small number? 0.0000000000000000000000045691 • rationals 2/3 • irrationals 2 • transcendentals e, š ECE468 ALU-III.16 2002-2-27 

9 . Recall Scientific Notation decimal point exponent Sign, magnitude 23 -24 6.02 x 10 1.673 x 10 Mantissa radix (base) Sign, magnitude E - 127 IEEE F.P. ± 1.M x 2 Issues: ° Arithmetic (+, -, *, / ) ° Representation, Normal form ° Range and Precision ° Rounding ° Exceptions (e.g., divide by zero, overflow, underflow) ° Errors ° Properties ( negation, inversion, if A > B then A - B > 0 ) ECE468 ALU-III.17 2002-2-27 Floating-Point Arithmetic Representation of floating point numbers in IEEE 754 standard: 1 8 23 single precision sign S E M Exponent: mantissa: excess 127 Sign + Magnitude, normalized binary integer binary significand w/ hidden integer bit: 1.M actual exponent is e = E - 127 0 < E < 255, not 0 ≤ E ≤ 255 127 < e < 128, not –127 ≤ e ≤ 128 S E-127 00000000 is reserved for 0; 11111111 is reserved for infinity. N = (-1) 2 (1.M) e.g. 0 = 0 00000000 0 . . . 0 -1.5 = 1 01111111 10 . . . 0 Magnitude of numbers that can be represented is in the range: -126 127 2 (1.0) to 2 (2 - 2 23 ) which is approximately: -38 38 1.8 x 10 to 3.40 x 10 ECE468 ALU-III.18 2002-2-27 

10 . Normalized Numbers Significand is left adjusted --> as large as possible, exponent is as small as possible 4 E.g., B = 2 , p = 3: (once used in IBM 360/370, p.280) 0 0110 0000 . 0110 1100 = 0.6C 0 0101 0110 . 1100 0000 = 6.C0 denormalized normalized In B = 2, the significand MSB is always 1 when the significand is left adjusted. So not necessary to store this "hidden" bit in memory. 0 011 1.01 1 0 011 .011 w/o hidden bit w/ hidden bit = improved precision Within the FPU, the hidden bit is inserted because of the denormalization step that precedes FP add/subtract. -bias 2 must distinguish from Smallest normal #: 0 0 ... 0 .0 ... 01 hidden bit zero with special form "1" 0 0…0 .0…00, no hidden bit 0 0 ... 0 1.0 ... 00 no hidden bit ECE468 ALU-III.19 2002-2-27 Double Precision for greater precision and larger range Representation of floating point numbers in double precision: 1 11 20+32 single precision sign S E M Exponent: mantissa: excess 1023 Sign + Magnitude, normalized binary integer binary significand w/ hidden actual exponent is integer bit: 1.M e = E - 1023 0 < E < 2047 S E-1023 N = (-1) 2 (1.M) 0 = 0 00000000 0 . . . 0 -1.5 = 1 01111111 10 . . . 0 Questions: Why is FP number normalized? (for accuracy) Why is FP not accurate for large numbers? Why is S put on leftmost? (P.278) Why is E represented by biased notation? (P.278) Why is E put before M? (P.278) ECE468 ALU-III.20 2002-2-27 

11 . Basic Addition Algorithm (pp 280-285) For addition (or subtraction) this translates into the following steps: (1) compute Ye - Xe, supposing Ye > Xe. Xe-Ye (2) right shift Xm that many positions to form Xm 2 (3) compute Xm 2 Xe-Ye + Ym if representation demands normalization, then a normalization step follows: (4) left shift result, decrement result exponent and check for underflow right shift result, increment result exponent and check for overflow continue until MSB of data is 1 (NOTE: Hidden bit in IEEE Standard) (5) If significand is longer than allowed, round significand (6) if result is 0 mantissa, may need to set the exponent to zero by special step ECE468 ALU-III.21 2002-2-27 Basic Addition Algorithm (continue) P284 S tart Example (p282) 1. Compare the exponents of the two numbers. Shift the smaller number to the right until its expone nt would match the larger exponent 0.5 X – 0.4375 = (1.000x2-1 )X (-1.110x2-2 ) 2 . Add the significands Step1: -1.110x2-2 -0.111x2-1 3. Normalize the sum, either shifting right and incrementing the exponent or shifting left and decreme nting the expone nt Step2: 1.000x2-1 +( -0.111x2-1 ) = 0.001x2-1 Ove rflow or Y es unde rflow? Step3: 0.001x2-1 1.000x2–4 No Exception Step4: None 4. Round the significand to the appropriate numbe r of bits No Still normalized? Y es D one ECE468 ALU-III.22 2002-2-27 

12 . Datapath for FPU (See Fig. 4.45 for more details) E1 E2 AC MQ DR Exp adder Mantissa Unit adder Unit E Data Out Data In Addition Algorithm: AC<n m -1:0>, DR<nm -1:0>, E1<n m -1:0>, E2<n m -1:0>, E<n m -1:0>, AC_OVERFLOW, ERROR Begin: AC_OVERFLOW := 0; ERROR := 0; Load: E1:= Xe; AC := Xm; E2 := Ye; DR := Ym; ECE468 ALU-III.23 2002-2-27 Extra Bits "Floating Point numbers are like piles of sand; every time you move one you lose a little sand, but you pick up a little dirt." How many extra bits? IEEE: As if computed the result exactly and rounded. Addition: 1.xxxxx 1.xxxxx 1.xxxxx + 1.xxxxx 0.001xxxxx 0.01xxxxx 1x.xxxxy 1.xxxxxyyy 1x.xxxxyyy post-normalization pre-normalization pre and post °Guard Digits: digits to the right of the first p digits of significand to guard against loss of digits – can later be shifted left into first P places during normalization. °Addition: carry-out shifted in °Subtraction: borrow digit and guard °Multiplication: carry and guard, division requires guard ECE468 ALU-III.24 2002-2-27 

13 . Rounding Digits normalized result, but some non-zero digits to the right of the significand --> the number should be rounded E.g., B = 10, p = 3: 2-bias 0 2 1.69 = 1.6900 * 10 - 0 0 7.85 = - .0785 * 10 2-bias 0 2 1.61 = 1.6115 * 10 2-bias one round digit must be carried to the right of the guard digit so that after a normalizing left shift, the result can be rounded, according to the value of the round digit IEEE Standard: (p. 300) four rounding modes: round to nearest (default) round towards plus infinity (always round up) round towards minus infinity(always round down) round towards 0 round to nearest: round digit < B/2 then truncate > B/2 then round up (add 1 to ULP) = B/2 then round to nearest even digit it can be shown that this strategy minimizes the mean error introduced by rounding ECE468 ALU-III.25 2002-2-27 Infinity and NaNs (pp300-301) result of operation overflows, i.e., is larger than the largest number that can be represented overflow is not the same as divide by zero (raises a different exception) +/- infinity S 1...1 0...0 It may make sense to do further computations with infinity e.g., X/0 > Y may be a valid comparison Not a number, but not infinity (e.q. sqrt(-4)) invalid operation exception (unless operation is = or =) NaN S 1 . . . 1 non-zero HW decides what goes here NaNs propagate: f(NaN) = NaN ECE468 ALU-III.26 2002-2-27 

14 . Exceptions Invalid operation: result of operation is a NaN (except = or =) inf. +/- inf.; 0 * inf; 0/0; inf./inf.; x remainder y where y = 0; sqrt(x) where x < 0, x≠ ≠+/- inf. Overflow: result of operation is larger than largest representable # flushed to +/- inf. if overflow exception is not enabled Divide by 0: x/0 where x = 0, +/- inf.; flushed to +/- inf. if divide by zero exception not enabled Underflow: subnormal result(see p300) OR non-zero result underflows to 0 Inexact: rounded result not the actual result (rounding error = 0) IEEE Standard --> specifies defaults and allows traps to permit user to handle the exception contrast with the more usual result of aborting the computation altogether! ECE468 ALU-III.27 2002-2-27 Pentium Bug °Pentium FP Divider uses algorithm to generate multiple bits per steps • FPU uses most significant bits of divisor & dividend/remainder to guess next 2 bits of quotient • Guess is taken from lookup table: -2, -1,0,+1,+2 (if previous guess too large a reminder, quotient is adjusted in subsequent pass of -2) • Guess is multiplied by divisor and subtracted from remainder to generate a new remainder • Called SRT division after 3 people who came up with idea °Pentium table uses 7 bits of remainder + 4 bits of divisor = 211 entries °5 entries of divisors omitted: 1.0001, 1.0100, 1.0111, 1.1010, 1.1101 from PLA (fix is just add 5 entries back into PLA: cost $200,000) °Self correcting nature of SRT => string of 1s must follow error • e.g., 1011 1111 1111 1111 1111 1011 1000 0010 0011 0111 1011 0100 (2.99999892918) °Since indexed also by divisor/remainder bits, sometimes bug doesn’t show even with dangerous divisor value ECE468 ALU-III.28 2002-2-27 

15 . Pentium bug appearance °First 11 bits to right of decimal point always correct: bits 12 to 52 where bug can occur (4th to 15th decimal digits) °FP divisors near integers 3, 9, 15, 21, 27 are dangerous ones: • 3.0 > d 3.0 - 36 x 2–22 , 9.0 > d 9.0 - 36 x 2–20 • 15.0 > d 15.0 - 36 x 2–20 , 21.0 > d 21.0 - 36 x 2–19 °0.333333 x 9 could be problem °In Microsoft Excel, try (4,195,835 / 3,145,727) * 3,145,727 • = 4,195,835 => not a Pentium with bug • = 4,195,579 => Pentium with bug (assuming Excel doesn’t already have SW bug patch) • Rare since error in 5th significant digit ECE468 ALU-III.29 2002-2-27 Pentium Bug Time line °June 1994: Intel discovers bug in Pentium: takes months to make change, reverify, put into production: plans good chips in January 1995 4 to 5 million Pentiums produced with bug °Scientist suspects errors and posts on Internet in September 1994 °Nov. 22 Intel Press release: “Can make errors in 9th digit ... Most engineers and financial analysts need only 4 of 5 digits. Theoretical mathematician should be concerned. ... So far only heard from one.” °Intel claims happens once in 27,000 years for typical spread sheet user: • 1000 divides/day x error rate assuming numbers random °Dec 12: IBM claims happens once per 24 days: Bans Pentium sales • 5000 divides/second x 15 minutes = 4.2 million divides/day • IBM statement: http://www.ibm.com/Features/pentium.html • Intel said it regards IBM's decision to halt shipments of its Pentium processor-based systems as unwarranted. ECE468 ALU-III.30 2002-2-27 

16 . Pentium jokes °Q: What's another name for the "Intel Inside" sticker they put on Pentiums? A: Warning label. °Q: Have you heard the new name Intel has chosen for the Pentium? A: the Intel Inacura. °Q: According to Intel, the Pentium conforms to the IEEE standards for floating point arithmetic. If you fly in aircraft designed using a Pentium, what is the correct pronunciation of "IEEE"? A: Aaaaaaaiiiiiiiiieeeeeeeeeeeee! °TWO OF TOP TEN NEW INTEL SLOGANS FOR THE PENTIUM 9.9999973251 It's a FLAW, Dammit, not a Bug 7.9999414610 Nearly 300 Correct Opcodes ECE468 ALU-III.31 2002-2-27 Pentium conclusion: Dec. 21, 1994 $500M write-off “To owners of Pentium processor-based computers and the PC community: We at Intel wish to sincerely apologize for our handling of the recently publicized Pentium processor flaw. The Intel Inside symbol means that your computer has a microprocessor second to none in quality and performance. Thousands of Intel employees work very hard to ensure that this is true. But no microprocessor is ever perfect. What Intel continues to believe is technically an extremely minor problem has taken on a life of its own. Although Intel firmly stands behind the quality of the current version of the Pentium processor, we recognize that many users have concerns. We want to resolve these concerns. Intel will exchange the current version of the Pentium processor for an updated version, in which this floating-point divide flaw is corrected, for any owner who requests it, free of charge anytime during the life of their computer. Just call 1-800-628-8686.” Sincerely, Andrew S. Grove Craig R. Barrett Gordon E. Moore President /CEO Executive Vice President Chairman of the Board ECE468 ALU-III.32 &COO 2002-2-27 

17 . Summary °Bits have no inherent meaning: operations determine whether they are really ASCII characters, integers, floating point numbers °Divide can use same hardware as multiply: Hi & Lo registers in MIPS °Floating point basically follows paper and pencil method of scientific notation using integer algorithms for multiply and divide of significands °IEEE 754 requires good rounding; special values for NaN, Infinity °Pentium: Difference between bugs that board designers must know about and bugs that potentially affect all users • Why not make public complete description of bugs in later category? • $200,000 cost in June to repair design • $500,000,000 loss in December in profits to replace bad parts • How much to repair Intel’s reputation? °What is technologists responsibility in disclosing bugs? ECE468 ALU-III.33 2002-2-27