离散型随机变量

1 . 2-1: 离散型随机变量 张伟平 课件 http://staff.ustc.edu.cn/~zwp/ 论坛 http://fisher.stat.ustc.edu.cn 

2 .第二章随机变量及其分布 2.1 随机变量的概念 . . . . . . . . . . . . . . . . . 1 2.2 离散型随机变量 . . . . . . . . . . . . . . . . . 5 2.2.1 0-1 分布 . . . . . . . . . . . . . . . . . 8 2.2.2 二项分布 . . . . . . . . . . . . . . . . 9 2.2.3 几何分布 (Geometric distribution) . . 12 2.2.4 Pascal 分布 (负二项分布) . . . . . . . 16 2.2.5 Poisson 分布 . . . . . . . . . . . . . . 20 2.2.6 离散的均匀分布 . . . . . . . . . . . . . 27 Previous Next First Last Back Forward 1 

3 . 2.1 随机变量的概念 随机变量是其值随机会而定的变量。 ↑Example 以 X 表示掷一次骰子得到的点数, X 是一个随机变量. 它可以 取 {1, 2, 3, 4, 5, 6} 中的一个值，但到底取那个值，要等掷了骰子才知 道. ↓Example ↑Example 一张奖券的中奖金额是一个随机变量. 它的值要等开奖以后才知 道. ↓Example Previous Next First Last Back Forward 1 

4 . ↑Example 在一批产品中随机地抽出 100 个产品, 其中所含的废品数是一个 随机变量. 它的值要等检查了所有抽出的产品后才知道. ↓Example 在另外的例子中, 随机试验的结果虽然不是一个数, 但仍可用数 来描述. ↑Example 掷一枚硬币出现正面或反面. ↓Example     2, ω = ω1 X(ω) = 1, ω = ω2 , ω3    0, ω = ω4 ↑Example Previous Next First Last Back Forward 2 

5 . 产品被分为正品或废品. ↓Example 上面两例中的结果均可用一个取值 0,1 的随机变量来描述, 其中 可以 1 代表正面或正品, 以 0 代表反面或废品. 事实上, 对任意一个事件 A, 定义 { 1 ω∈A, IA (ω) = 0 反之 , 则事件 A 由随机变量 IA 表示出来. IA 称为事件 A 的示性函数. 随机变量是把随机试验的结果，也就是样本空间，与一组实数联 系起来. 这样的处理简化了原来的概率结构. 例如某机构调查民众对 一提案的态度是支持 (1) 还是反对 (0). 如果随机访问 50 人，按照 古典概型，所有可能的结果有 250 个. 但是如果我们用 X 记 1 的个 数来表示赞成者的人数，则 X 为一个随机变量. 它的取值范围只在 Previous Next First Last Back Forward 3 

6 .{0, 1, · · · , 50}. 所以随机变量的引进有利于我们对所研究的问题进行 准确, 简练的描述. 又由于随机变量取实值, 随机变量之间的运算就变 得容易了. 令 Ω 为一个样本空间. 令 X 是定义在 Ω 上的一个实函数, 如果对 Ω 中的任意点 ω，总存在一个实数 X(ω) 与之对应， Definition 则称 X 为一个 (一维) 随机变量. 常见的随机变量可以分为两大类. 只取有限个或可数个值的随机 变量称为离散型随机变量；取连续的值且密度存在的随机变量称为连 续型随机变量. 当然, 存在既非离散型也非连续型的随机变量. 但它们 在实际中并不常见, 也不是我们这里研究的对象. Previous Next First Last Back Forward 4 

7 . 2.2 离散型随机变量 设 X 为一随机变量. 如果 X 只取有限个或可数个值，则称 Definition X 为一个 (一维) 离散型随机变量. 由于一个随机变量的值是由试验结果决定的，因而是以一定的概 率取值. 这个概率分布称为离散型随机变量的概率函数. 设 X 为一离散型随机变量，其全部可能值为 {a1 , a2 , ...}. 则 pi = P (X = ai ), i = 1, 2, ... (2.1) Definition 称为 X 的概率质量函数 (probability mass function, pmf) 或分布律. Previous Next First Last Back Forward 5 

8 . 概率质量函数 {pi , i = 1, 2, ..} 必须满足下列条件： pi ≥ 0, i = 1, 2, .... ∑ pi = 1. i ∑ ∑ F (x) = P (X ≤ x) = P (X = ai ) = pi i:pi ≤x i:pi ≤x P (X = ai ) = P (ai−1 < X ≤ ai ) = F (ai ) − F (ai−1 ) 概率质量函数 (2.1) 指出了全部概率 1 是如何在 X 的所有可能值之 间分配的. 它可以列表的形式给出： 可能值 a1 a2 ... ai ... (2.2) 概率 p1 p2 ... pi ... 有时也把 (2.2) 称为随机变量 X 的分布表. Previous Next First Last Back Forward 6 

9 . 设 Ω 为一样本空间. X 为定义于其上的一个离散型随机变量， 其取值为 x1 , x2 , ..... 令 A 为 {x1 , x2 , ...} 的任意一个子集. 事件 {X 取值于 A 中} 的概率可根据概率的可加性来计算： ∑ P (A) = P (X = x). x∈A 这样知道了离散型随机变量 X 的概率函数，我们就能给出关于 X 的 任何概率问题的回答. 下 面 我 们 给 出 常 见 的 离 散 型 分 布. 在 描 述 离 散 概 率 模 型 时, Bernoulli 试验是最早被研究且应用及其广泛的概率模型. ¯ 则称此试验为一 设一个随机试验只有两个可能结果 A 和 A, Definition Bernoulli 试验. Previous Next First Last Back Forward 7 

10 .设将一个可能结果为 A 和 A¯ 的 Bernoulli 试验独立地重 复 n 次, 使得事件 A 每次出现的概率相同, 则称此试验为 Definition n 重 Bernoulli 试验. 下面的 0-1 分布和二项分布都是以 Bernoulli 试验为基础的. 2.2.1 0-1 分布 设随机变量 X 只取 0,1 两值，P (X = 1) = p，P (X = 0) = 1 − p，则称 X 服从 0-1 分布或 Bernoulli 分布. 0-1 分布是很多古典 概率模型的基础. Previous Next First Last Back Forward 8 

11 .2.2.2 二项分布 设某事件 A 在一次试验中发生的概率为 p. 现把试验独立地重复 n 次. 以 X 记 A 在这 n 次试验中发生的次数，则 X 取值 0, 1, ..., n， 且有 ( ) n k P (X = k) = p (1 − p)n−k , k = 0, 1, · · · , n. (2.3) k 称 X 服从二项分布，记为 X ∼ B(n, p). dbinom(0:20, 20, 0.5) dbinom(0:20, 20, 0.8) 0.20 0.10 0.10 0.00 0.00 5 10 15 20 5 10 15 20 Index Index Previous Next First Last Back Forward 9 

12 . 从 ( ) ∑n n k p (1 − p)n−k = (p + 1 − p)n = 1, i=1 k 我们知道 (2.3) 确实是一个概率函数. in R ↑Code dbinom, rbinom, pbinom, qbinom ↓Code 为了考察这个分布是如何产生的，考虑事件 {X = i}. 要使这个 事件发生，必须在这 n 次试验的原始记录 ¯ AAAA... ¯ A¯ AA 中，有 i 个 A, n − i 个 A, ¯ 每个 A 有概率 p 而每个 A¯ 有概率 1 − p. 又由于每次试验独立，所以每次出现 A 与否与其它次试验的结果独 立. 因此由概率乘法定理得出每个这样的原始结果序列发生的概率为 Previous Next First Last Back Forward 10 

13 . ( ) pi (1 − p)n−i . 但是 i 个 A 和 n − i 个 A¯ 的排列总数是 nk ，所以有 i 个 A 的概率是： ( ) n i P (X = i) = p (1 − p)n−i , i = 0, 1, · · · , n. i 由 npn → λ > 0，因此 pn → 0，从而 ( ) n k 1 n(n − 1) · · · (n − k + 1) pn (1 − pn )n−k = (npn )k (1 − pn )n (1 − pn )−k k k! nk 1 k −λ → λ e k! 最后是因为 |(1 − pn )n − (1 − n ) | ≤ n|(1 − pn ) − (1 − n λ n λ )| = |npn − λ| → 0 −λ 以及 (1 − n ) → e 。 λ n 一个变量服从二项分布有两个条件： • 各次试验的条件是稳定的，这保证了事件 A 的概率 p 在各次 试验中保持不变 Previous Next First Last Back Forward 11 

14 . • 各次试验的独立性 现实生活中有许多现象不同程度地满足这些条件. 例如工厂每天 生产的产品. 假设每日生产 n 个产品. 若原材料质量，机器设备，工 人操作水平等在一段时间内保持稳定，且每件产品是否合格与其它产 品合格与否并无显著性关联，则每日的废品数服从二项分布. 2.2.3 几何分布 (Geometric distribution) 在 n 重贝努里实验中，当试验次数 n → ∞ 时，称为可列重 Definition 贝努里试验。 若以 X 表示在可列重贝努里试验中结果 A 出现时的试验次数， 即若以“成功”表示结果 A 发生，p = P (A) = 1 − q，则 X 表示首 Previous Next First Last Back Forward 12 

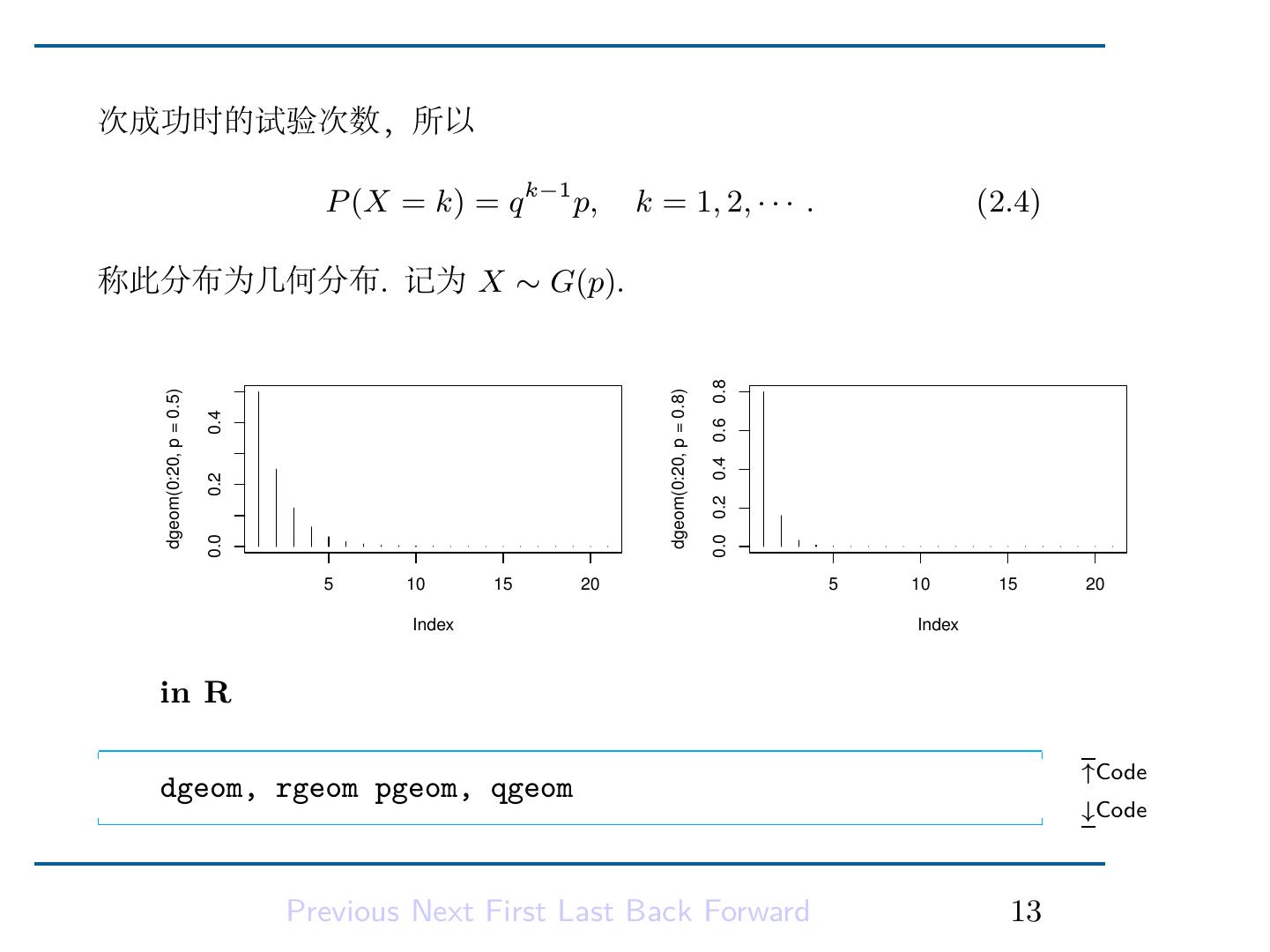
15 .次成功时的试验次数，所以 P (X = k) = q k−1 p, k = 1, 2, · · · . (2.4) 称此分布为几何分布. 记为 X ∼ G(p). 0.0 0.2 0.4 0.6 0.8 dgeom(0:20, p = 0.5) dgeom(0:20, p = 0.8) 0.4 0.2 0.0 5 10 15 20 5 10 15 20 Index Index in R ↑Code dgeom, rgeom pgeom, qgeom ↓Code Previous Next First Last Back Forward 13 

16 . ↑Example 一个人要开门, 他共有 n 把钥匙。其中仅有一把可以打开门。现 随机地有放回的从中选取一把开门，若不成功再放回去重新随机选取 一把开门，问这人在第 S 次才首次试开成功的概率。 ↓Example 定理 1. 以所有正整数为取值集合的随机变量 ξ 服从几何分布 G(p), 当且仅当对任何正整数 m 和 n, 都有 P (ξ > m + n | ξ > m) = P (ξ > n). (2.5) 这个性质称为几何分布的无记忆性 (memoryless property). 证:设随机变量 ξ 服从几何分布 G(p), 写 q = 1 − p, 那么对任何 非负整数 k, 都有 ∑ ∞ ∑ ∞ P (ξ > k) = P (ξ = j) = p q j−1 = q k . j=k+1 j=k+1 Previous Next First Last Back Forward 14 

17 .所以对任何正整数 m 和 n, 都有 P (ξ > m + n, ξ > m) P (ξ > m + n | ξ > m) = P (ξ > m) P (ξ > m + n) q m+n = = = q n = P (ξ > n). P (ξ > m) qn 故知 (2.5) 式成立. 反之, 设对任何正整数 m 和 n, 都有 (2.5) 式成立. 对非负整数 k, 我们记 pk = P (ξ > k) . 于是由 (2.5) 式知, 对任何正整数 k, 都有 pk > 0, 并且对任何正整数 m 和 n, 都有 pm+n = pm · pn . 由此等式 立知, 对任何正整数 m, 都有 pm = pm 1 . 由于 p1 > 0, 而若 p1 = 1, 则 必导致对一切正整数 m, 都有 pm = 1, 此为不可能, 所以对某个小于 1 的正数 q, 有 p1 = q. 由此不难得, 对任何正整数 m, 都有 P (ξ = m) = P (ξ > m−1)−P (ξ > m) = pm−1 −pm = q m−1 −q m = p q m−1 , 其中 p = 1 − q, 所以 ξ 服从几何分布 G(p). Previous Next First Last Back Forward 15 

18 .2.2.4 Pascal 分布 (负二项分布) 在可列重贝努里试验中，若以 Xr 表示第 r 次成功发生时的试验 次数，则 Xr 的分布律为 P (Xr = k) = P ({前k − 1次恰有r − 1次成功且第k次成功}) = P ({前k − 1次恰有r − 1次成功})P ({第k次成功}) = r−1 r−1 k−r Ck−1 p q ·p = r−1 r k−r Ck−1 p q , k = r, r + 1, · · · . 称此概率分布为 Pascal 分布。 in R ↑Code dnbinom, rnbinom, pnbinom, qnbinom P (Xr = k)=dnbinom(k-r,size=r,prob=p) ↓Code Previous Next First Last Back Forward 16 

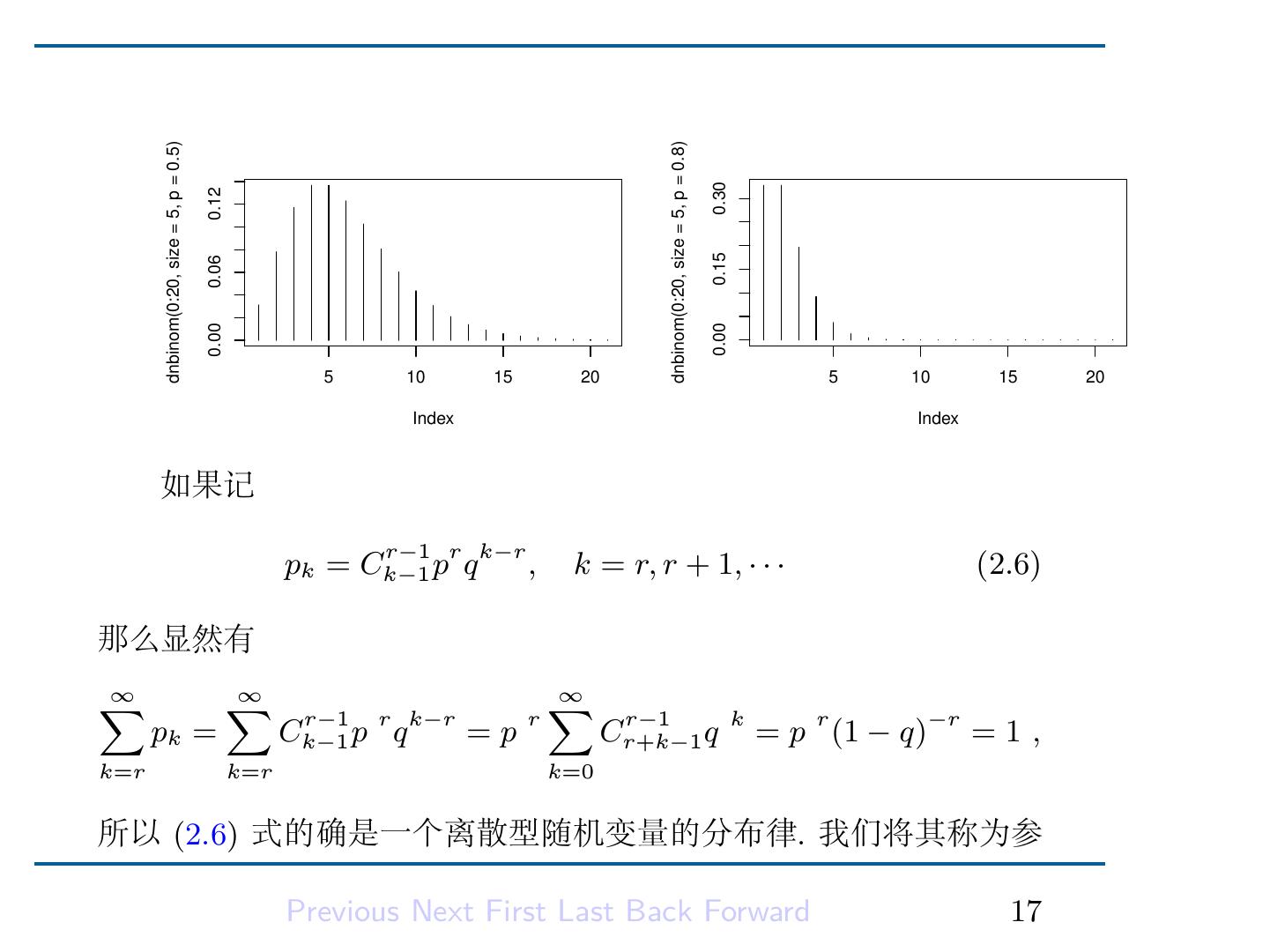
19 . dnbinom(0:20, size = 5, p = 0.5) dnbinom(0:20, size = 5, p = 0.8) 0.30 0.12 0.15 0.06 0.00 0.00 5 10 15 20 5 10 15 20 Index Index 如果记 r−1 r k−r pk = Ck−1 p q , k = r, r + 1, · · · (2.6) 那么显然有 ∑ ∞ ∑ ∞ ∑ ∞ pk = r−1 r k−r Ck−1 p q =p r r−1 Cr+k−1 q k = p r (1 − q)−r = 1 , k=r k=r k=0 所以 (2.6) 式的确是一个离散型随机变量的分布律. 我们将其称为参 Previous Next First Last Back Forward 17 

20 .数为 p 和 r 的 Pascal 分布. 又因为上式表明, 它可以用负二项展开 式中的各项表示, 所以又称为负二项分布. ↑Example ( Banach 火柴问题) 某人口袋里放有两盒火柴, 每盒装有火柴 n 根. 他每次随机取出一盒, 并从中拿出一根火柴使用. 试求他取出一 盒, 发现已空, 而此时另一盒中尚余 r 根火柴的概率. ↓Example 解: 以 A 表示甲盒已空, 而此时乙盒中尚余 r 根火柴的事件. 由 对称性知, 所求的概率等于 2P (A). 我们将每取出甲盒一次视为取得 一次成功, 以 ξ 表示取得第 n + 1 次成功时的取盒次数, 则 ξ 服从参 数为 0.5 和 n + 1 的 Pascal 分布 (因为每次取出甲盒的概率是 0.5). 易知, 事件 A 发生, 当且仅当 ξ 等于 2n − r + 1. 所以所求的概率等于 2P (A) = 2P (ξ = 2n − r + 1) = C2n−r n 2 r−2n . Previous Next First Last Back Forward 18 

21 . ↑Example 在可列重贝努里试验中，求事件 E ={n 次成功发生在 m 次失 败之前} 的概率。 ↓Example 解: 记 Fk ={第 n 次成功发生在第 k 次试验}, 则 ∪ n+m−1 E= Fk k=n 且诸 Fk 两两互斥，故 ∑ n+m−1 ∑ n+m−1 n−1 n k−n P (E) = P (Fk ) = Ck−1 p q . k=n k=n Previous Next First Last Back Forward 19 

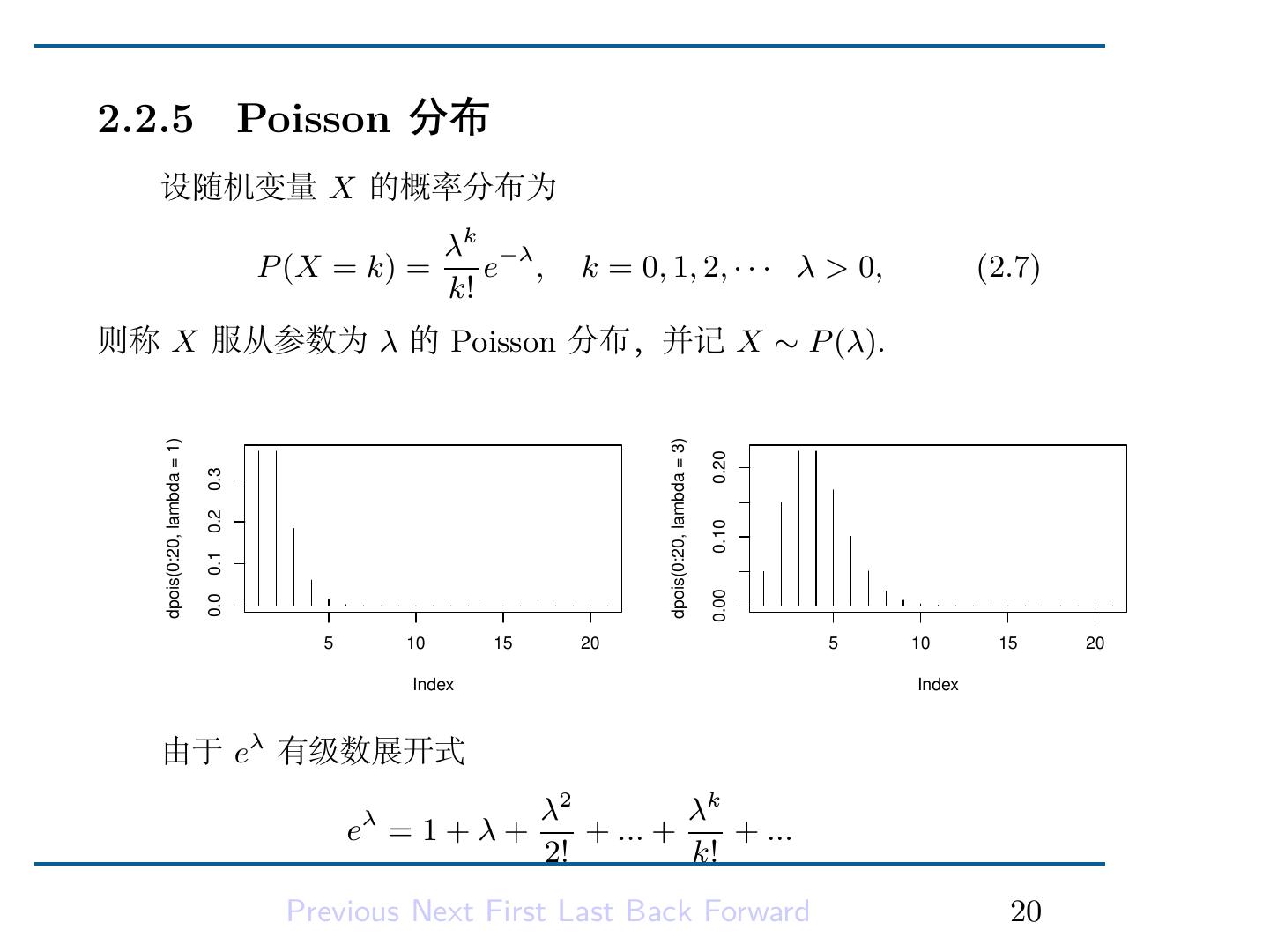
22 .2.2.5 Poisson 分布 设随机变量 X 的概率分布为 λk −λ P (X = k) = e , k = 0, 1, 2, · · · � λ > 0, (2.7) k! 则称 X 服从参数为 λ 的 Poisson 分布，并记 X ∼ P (λ). dpois(0:20, lambda = 1) dpois(0:20, lambda = 3) 0.20 0.3 0.2 0.10 0.1 0.00 0.0 5 10 15 20 5 10 15 20 Index Index 由于 eλ 有级数展开式 λ2 λk eλ = 1 + λ + + ... + + ... 2! k! Previous Next First Last Back Forward 20 

23 .所以 ∑ ∞ P (X = k) = 1. k=0 in R ↑Code dpois, rpois, ppois, qpois ↓Code ↑Example 假定体积为 V 的液体包含有一个大数目 N 的微生物. 再假定微 生物没有群居的本能, 它们能够在液体的任何部分出现，且在体积相 等的部分出现的机会相同. 现在我们取体积为 D 的微量液体在显微 镜下观察，问在这微量液体中将发现 x 个微生物的概率是什么？ ↓Example 我们假定 V 远远大于 D. 由于假定了这些微生物是以一致的概 率在液体中到处散布，因此任何一个微生物在 D 中出现的概率都是 Previous Next First Last Back Forward 21 

24 .D/V . 再由于假定了微生物没有群居的本能，所以一个微生物在 D 中的出现，不会影响另一个微生物在 D 中的出现与否. 因此微生物 中有 x 个在 D 中出现的概率就是 ( )( ) ( )N −x x N D D 1− . (2.8) x V V 在这里我们还假定微生物是如此之小, 拥挤的问题可以忽略不考虑, 即 N 个微生物所占据的部分对于体积 D 来说是微不足道. 在 (2.8) 中令 V 和 N 趋向于无穷, 且微生物的密度 N /V = d 保持常数. 将 (2.8) 式改写成如下形式： ( )x ( )N −x N (N − 1)(N − 2)...(N − x + 1) N D ND 1 − x!N x V NV ( ) ( )( ) ( ) Dd N −x 1 − N 1 − N ... 1 − N (Dd) 1 − N 1 2 x−1 x = . x! 当 N 变成无限时其极限为 e−Dd (Dd)x /x! (2.9) Previous Next First Last Back Forward 22 

25 .令 Dd = λ，则 (2.9) 和 (2.7) 的形式相同. 这一推导过程还证明了 λ 是 x 的平均数，因为所考察的一部分体积 D 乘以整个的密度 d 就给 出了在 D 中所预计的平均数目. 当 N 很大，p 很小且 N p 趋于一个极限时，Poisson 分布是二项 分布的一个很好的近似. 而在 N 未知时，Poisson 分布更显得有用. 我们有下面的定理. 定理 2. 在 n 重 Bernoulli 试验中, 以 pn 代表事件 A 在试验中出现 的概率, 它与试验总数 n 有关. 如果 npn → λ, 则当 n → ∞ 时, ( ) n k λk −λ pn (1 − pn )n−k → e . (2.10) k k! Previous Next First Last Back Forward 23 

26 . ↑Example 现在需要 100 个符合规格的元件. 从市场上买的该元件有废品率 0.01. 考虑到有废品存在, 我们准备买 100 + a 个元件使得从中可以 挑出 100 个符合规格的元件. 我们要求在这 100 + a 个元件中至少有 100 个符合规格的元件的概率不小于 0.95. 问 a 至少要多大? ↓Example 解: 令 A = {在100 + a个元件中至少有100个符合规格的元件}. 假定各元件是否合格是独立的. 以 X 记在 100 + a 个元件中的废品 数. 则 X 服从 n = 100 + a 和 p = 0.01 的二项分布, 且 ( ) ∑a 100 + a P (A) = P (X ≤ a) = (0.01)i (0.99)100+a−i . i=0 i 上 式 中 的 概 率 很 难 计 算. 由 于 100 + a 较 大 而 0.01 较 小, 且 (100 + a)(0.01) = 1 + 0.01a ≈ 1, 我们以 λ = 1 的 Poisson 分布来近 Previous Next First Last Back Forward 24 

27 .似上述概率. 因而 ∑ a P (A) = e−1 /i!. i=0 当 a = 0, 1, 2, 3 时, 上式右边分别为 0.368, 0.736, 0.920 和 0.981. 故 取 a = 3 已够了. ↑Example 假设一块放射性物质在单位时间内发射出的 α 粒子数 ξ 服从参 数为 λ 的 Poisson 分布。而每个发射出来的 α 粒子被记录下来的概 率是 p，就是说有 q = 1 − p 的概率被记数器漏记。如果各粒子是否 被记数器记录是相互独立的，试求记录下来的 α 粒子数 η 的分布。 ↓Example 解: 以事件 {ξ = n}, n = 0, 1, 2, · · · 为划分，则由全概率公式有 Previous Next First Last Back Forward 25 

28 . ∑ ∞ P (η = k) = P (η = k|ξ = n)P (ξ = n) n=0 ( ) ∑ ∞ n k n−k λn −λ = p q e n=k k n! ∑∞ (λq)n−k −λ (λp)k −λp = e (λp)k = e , k = 0, 1, 2, · · · .# n=k k!(n − k)! k! Previous Next First Last Back Forward 26 

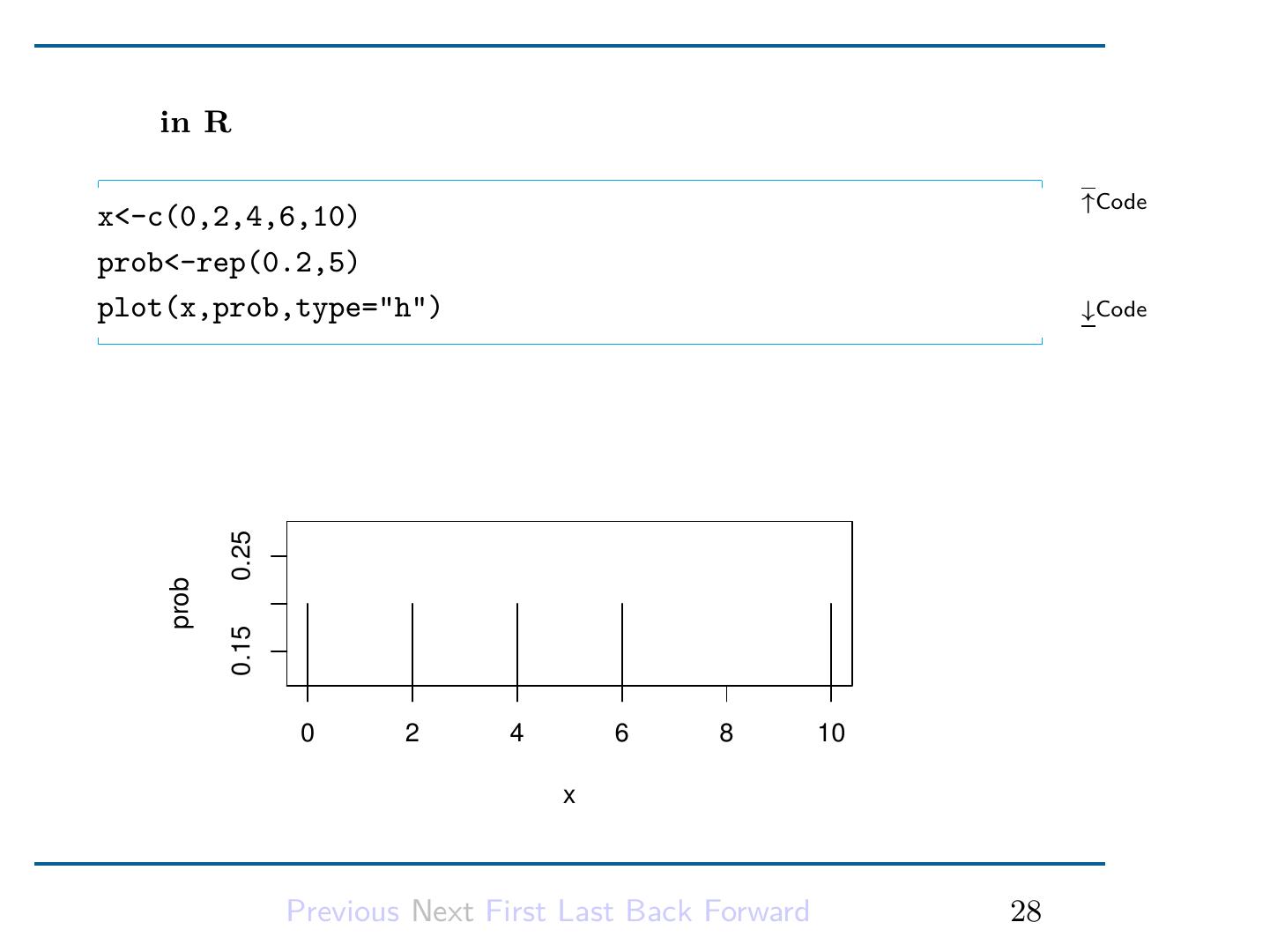
29 .2.2.6 离散的均匀分布 设随机变量 X 取值 a1 , a2 , ..., an , 且有 1 P (X = ak ) = , k = 1, ..., n. (2.11) n 则称 X 服从离散的均匀分布. 可以看出, 离散的均匀分布正是古典概型的抽象. Previous Next First Last Back Forward 27