1 .Directed Graphs 3/6/12 1

2 .Normal Person’s Graph x y y = f(x) 3/6/12 2

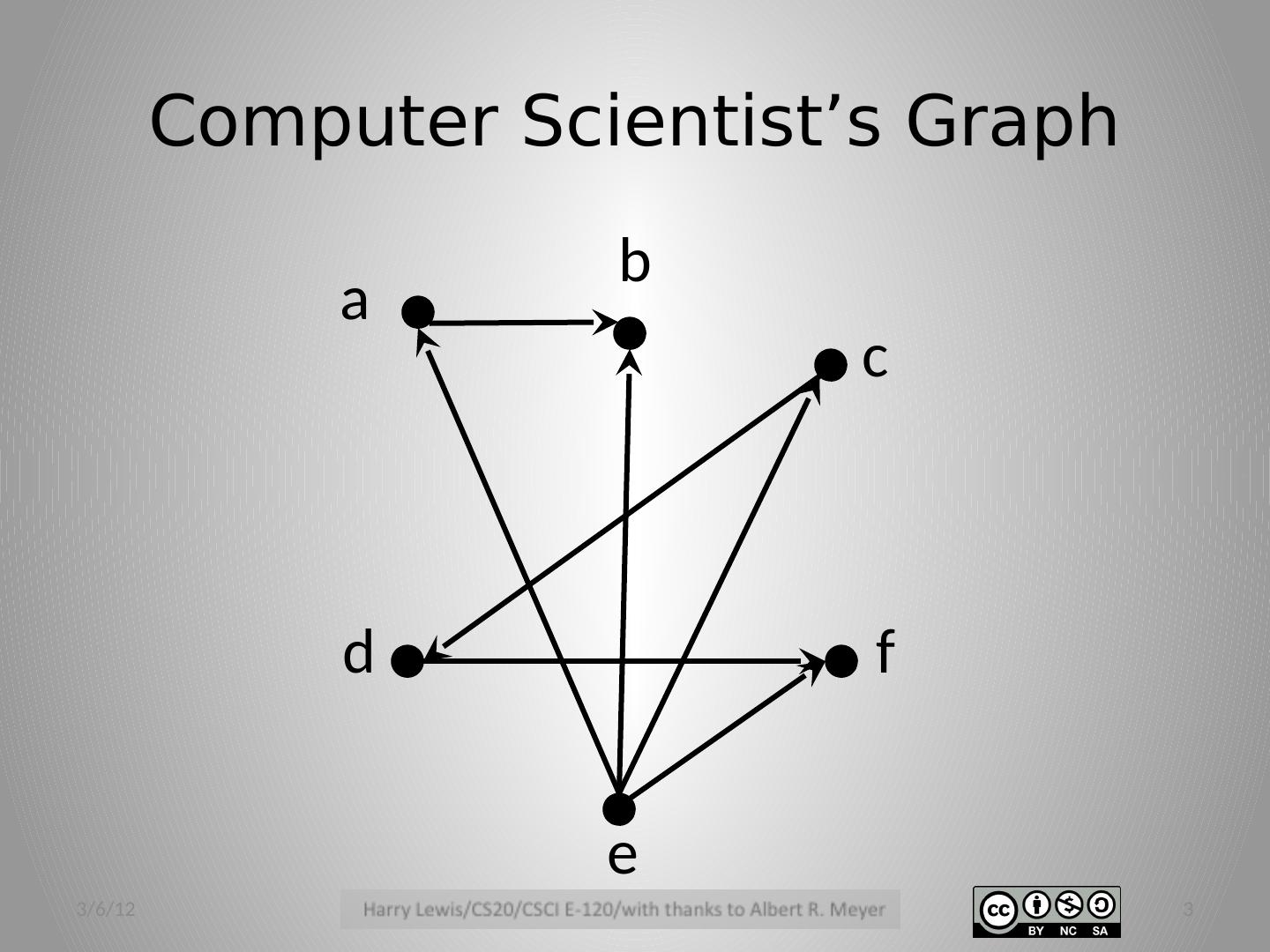
3 .Computer Scientist’s Graph a f e c d b 3/6/12 3

4 .Digraphs a set, V , of vertices a ka “nodes” a set, E ⊆ V × V of directed edges ( v,w ) ∈ E v w notation: v → w 3/6/12 4

5 .Relations and Graphs a c b d V = { a , b , c , d } E = {( a,b ), ( a,c ), ( c,b )} 3/6/12 5

6 .Formally, a digraph with vertices V is the same as a binary relation on V . Digraphs 3/6/12 6

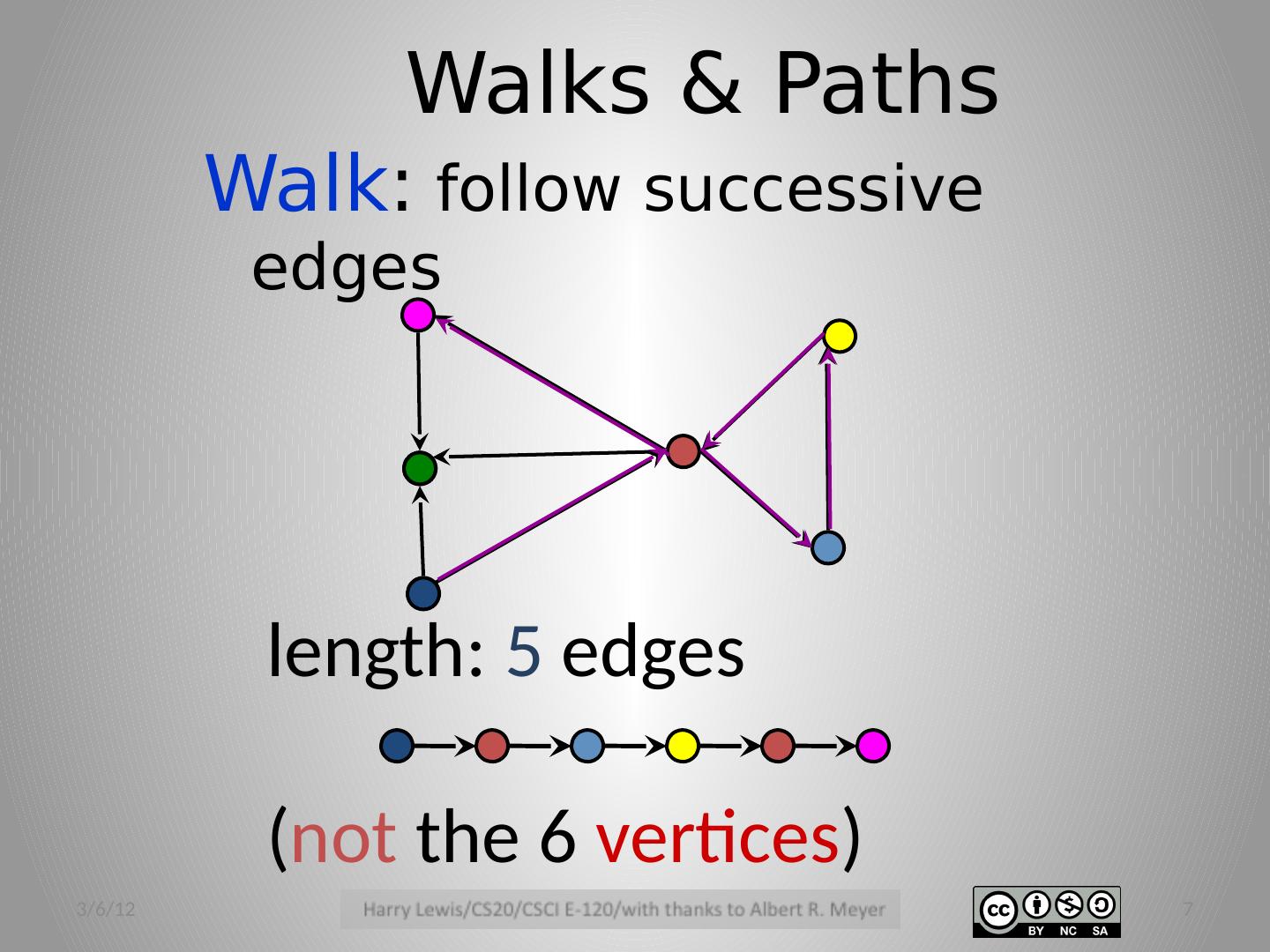
7 .Walks & Paths Walk : follow successive edges length: 5 edges ( not the 6 vertices ) 3/6/12 7

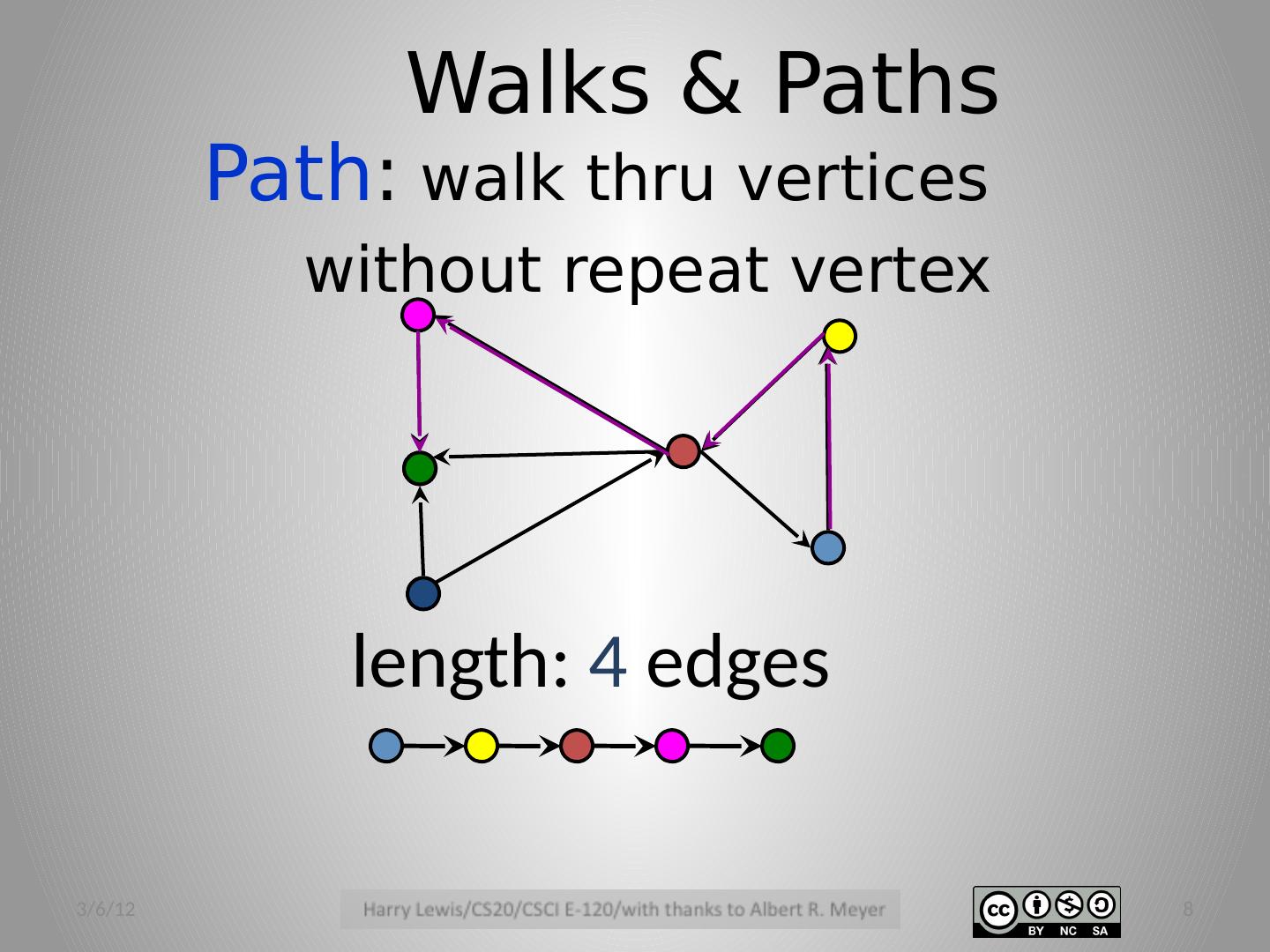
8 .Walks & Paths Path : walk thru vertices without repeat vertex length: 4 edges 3/6/12 8

9 .Lemma: The shortest walk between two vertices is a path! Proof: (by contradiction ) suppose path from u to v crossed itself: u v c Walks & Paths 3/6/12 9

10 .Proof: (by contradiction ) suppose path from u to v crossed itself: u v c then path without c---c is shorter ! Lemma: The shortest walk between two vertices is a path! Walks & Paths 3/6/12 10

11 .Walks & Paths Digraph G defines walk relation G + u G + v iff ∃ walk u to v (the positive walk relation ) “ + ” means 1 or more 3/6/12 11

12 .Walks & Paths Digraph G defines walk relation G * u G * v iff u to v (the walk relation ) “*” means “0 or more” 3/6/12 12

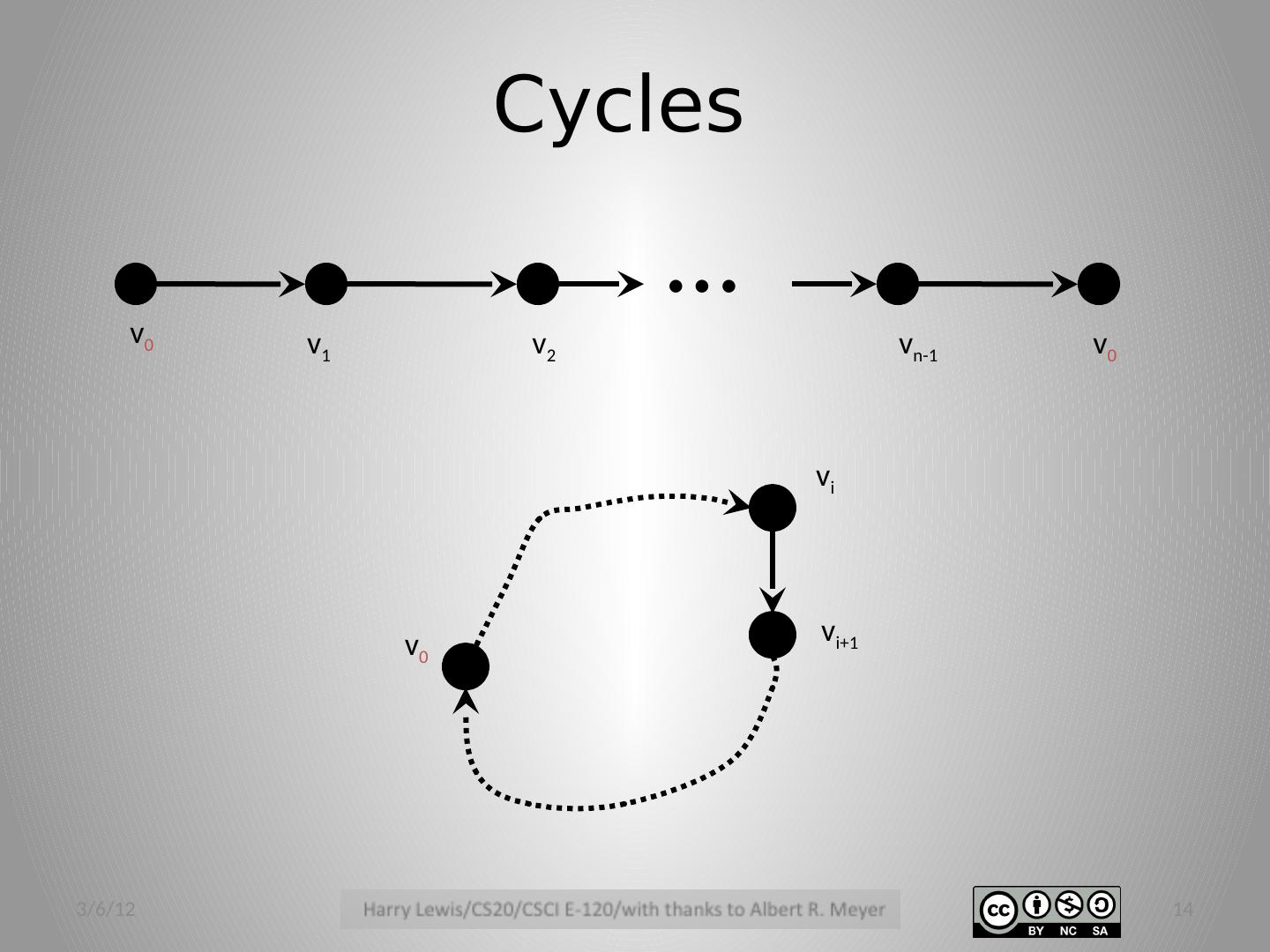
13 .Cycles A cycle is a walk whose only repeat vertex is its start & end. (a single vertex is a length 0 cycle) 3/6/12 13

14 .… v 0 v 1 v 2 v n-1 v 0 v 0 v i v i+1 Cycles 3/6/12 14

15 .Closed walk starts & ends at the same vertex. Lemma: The shortest positive length closed walk containing a vertex is a positive length cycle! Proof : similar Closed Walks & Cycles 3/6/12 15

16 .has no positive length cycle D irected A cyclic G raph DAG lec 7M. 16 3/6/12 16

17 .examples: < relation on integers ⊊ relation on sets prerequisite on classes D irected A cyclic G raph DAG 3/6/12 17

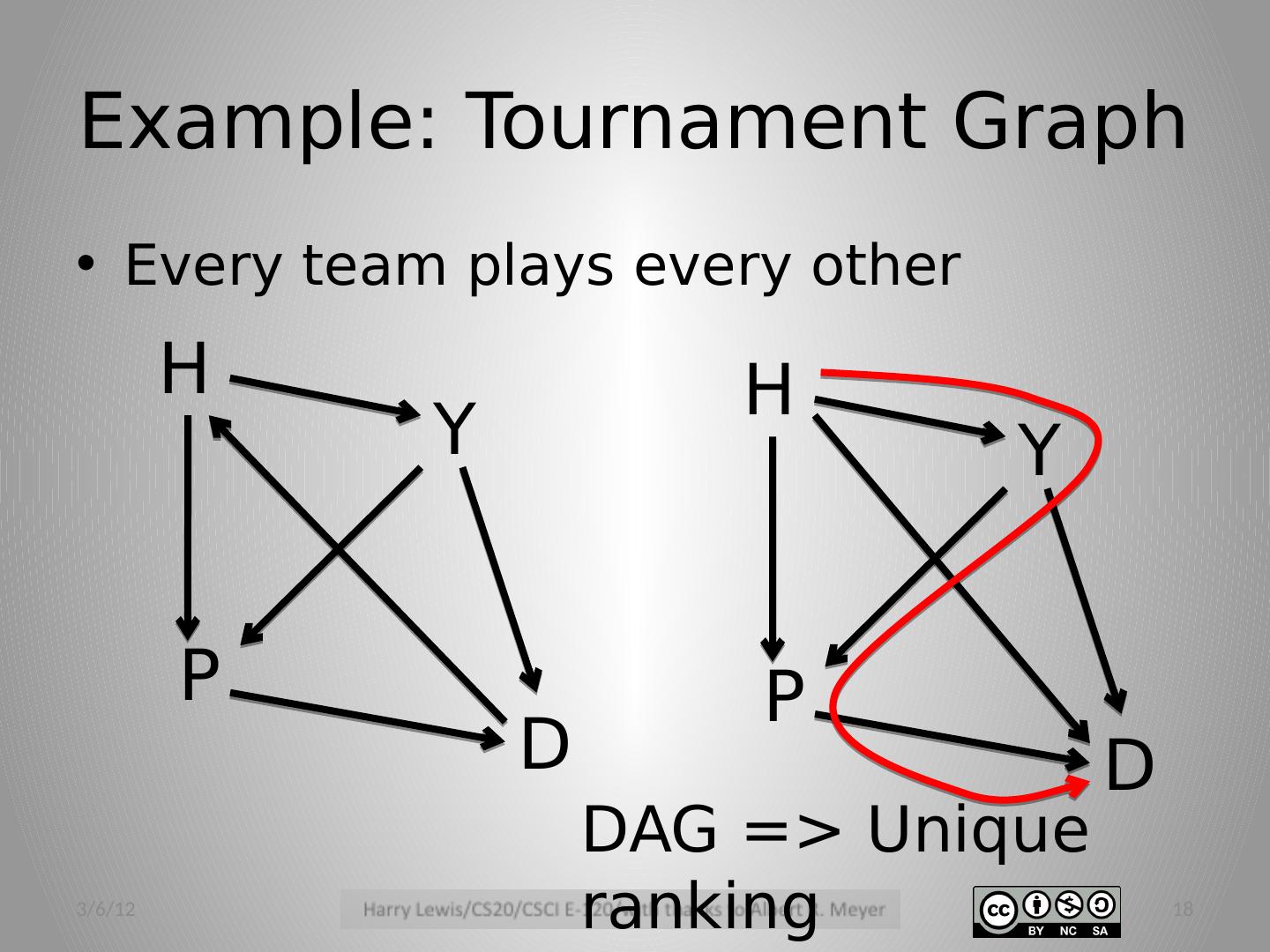
18 .Example: Tournament Graph Every team plays every other 3/6/12 18 H Y P D H Y P D DAG => Unique ranking