- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
数字逻辑结构的应用
展开查看详情
1 .Chapter 3 Digital Logic Structures
2 .Chapter 3 Digital Logic Structures
3 .Full Adder 3- 3 Consider computing 7+6=13: Now, consider one column of this addition: A combinational logic design
4 .1-bit Full Adder 3- 4 Truth table for a 1-bit adder: Formulate a circuit for each output
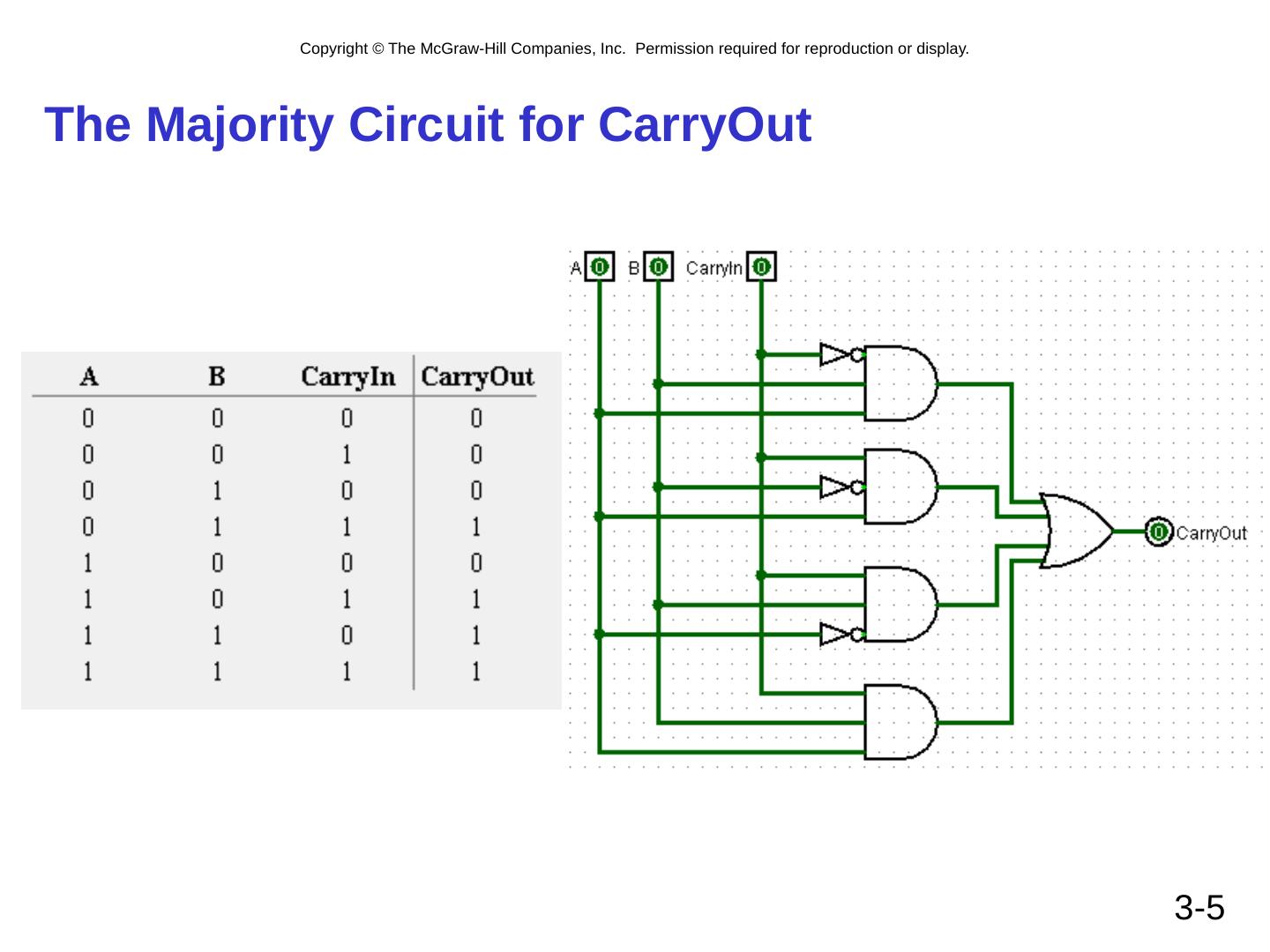
5 .The M ajority Circuit for CarryOut 3- 5
6 .Odd-Parity Circuit for the Sum 3- 6
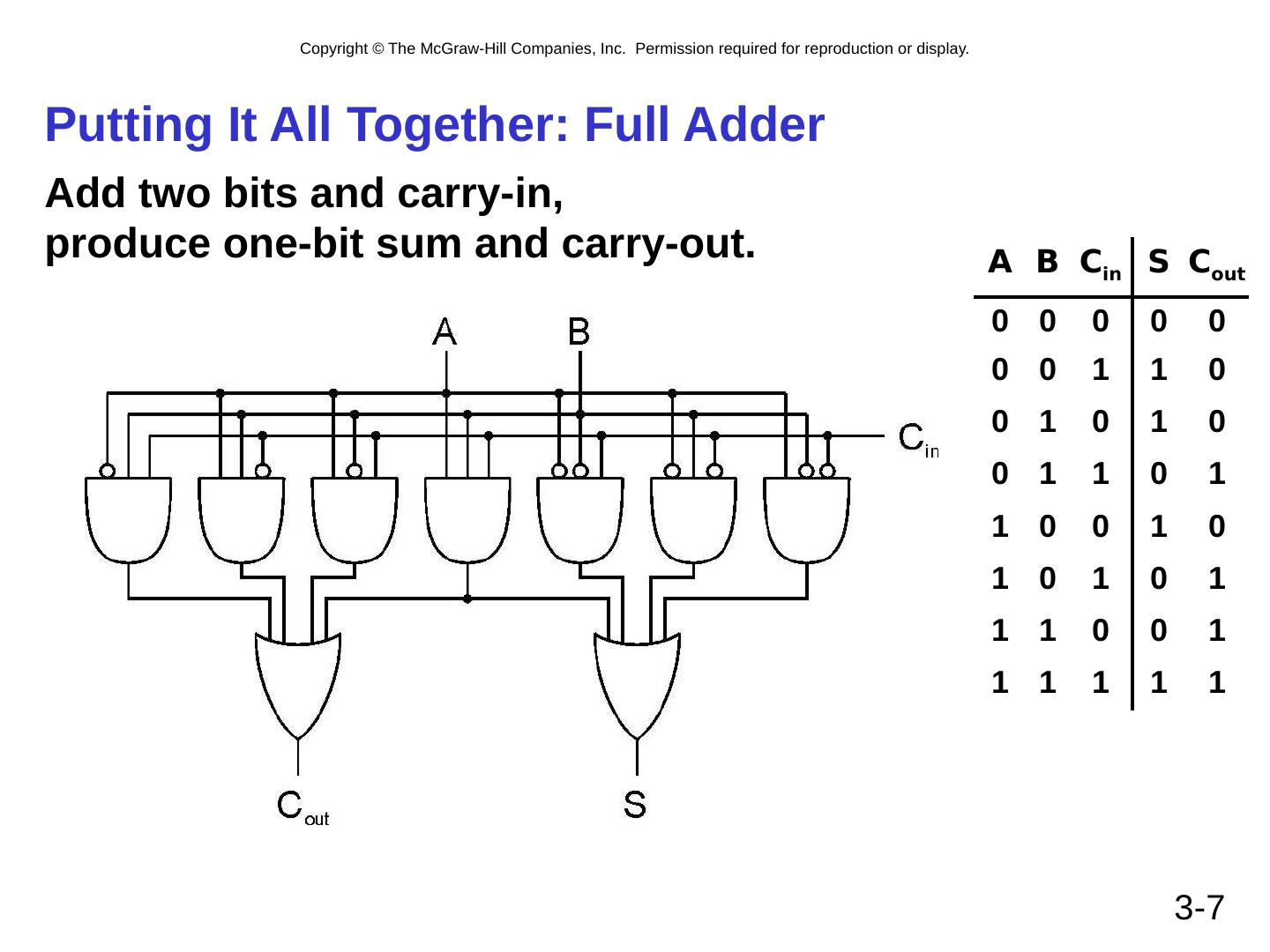
7 .3- 7 Putting It All Together: Full Adder Add two bits and carry-in , produce one-bit sum and carry-out. A B C in S C out 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1
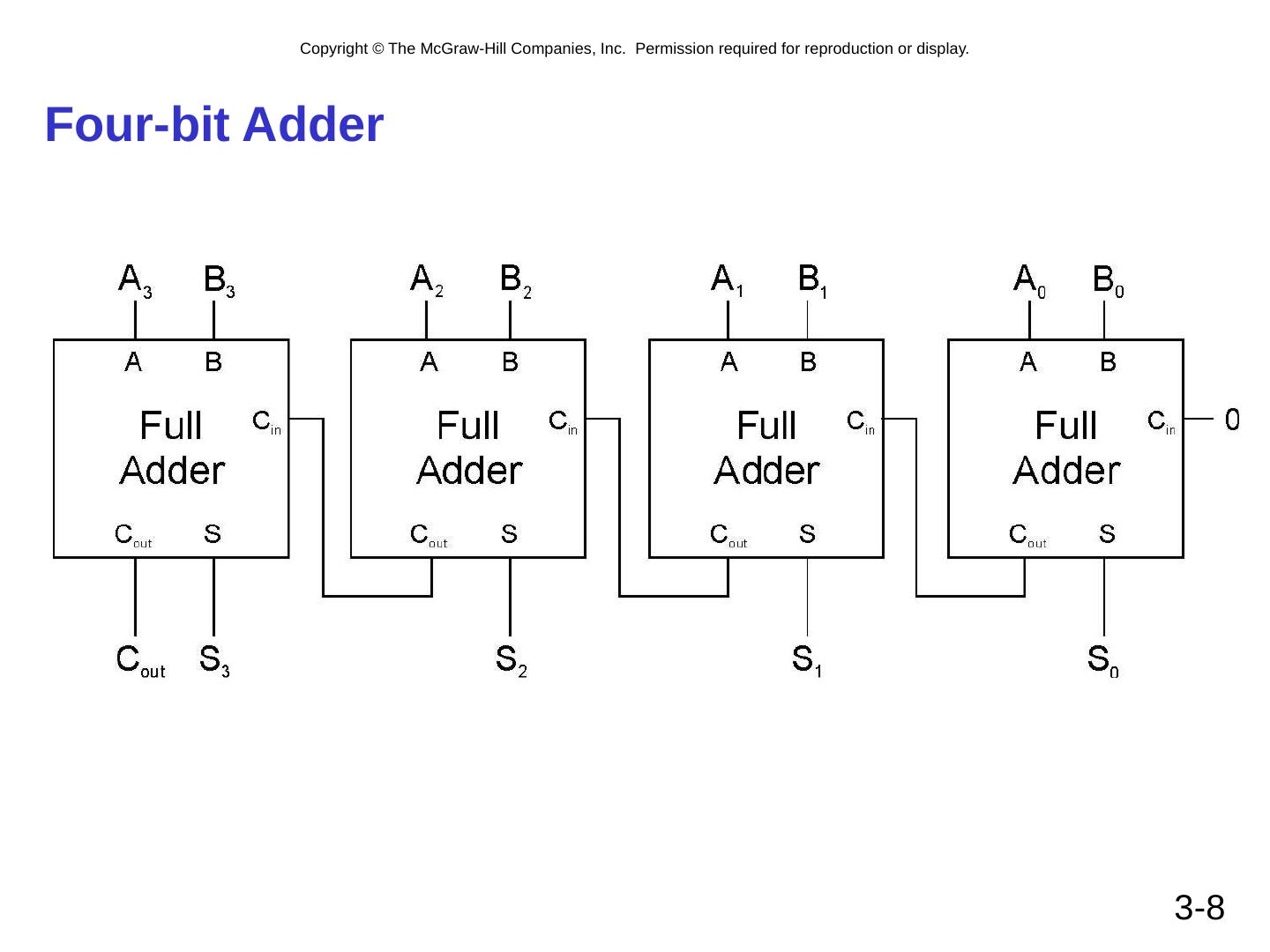
8 .3- 8 Four-bit Adder
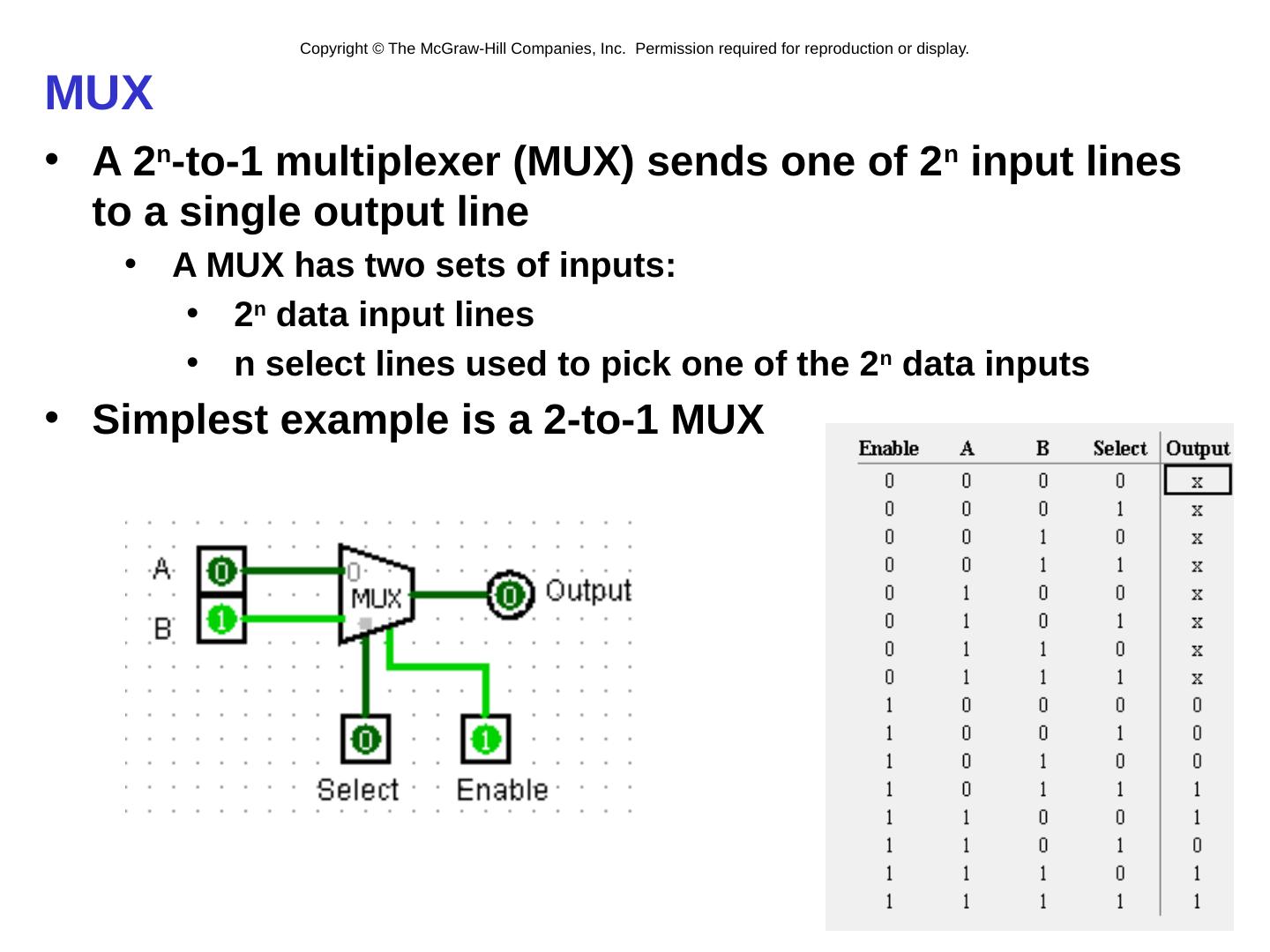
9 .Multiplexer (MUX) A device with multiple inputs and 1 output Could be used to allocate a resource to one of multiple clients: 3- 9
10 .MUX A 2 n -to-1 multiplexer (MUX) sends one of 2 n input lines to a single output line A MUX has two sets of inputs: 2 n data input lines n select lines used to pick one of the 2 n data inputs Simplest example is a 2-to-1 MUX 3- 10
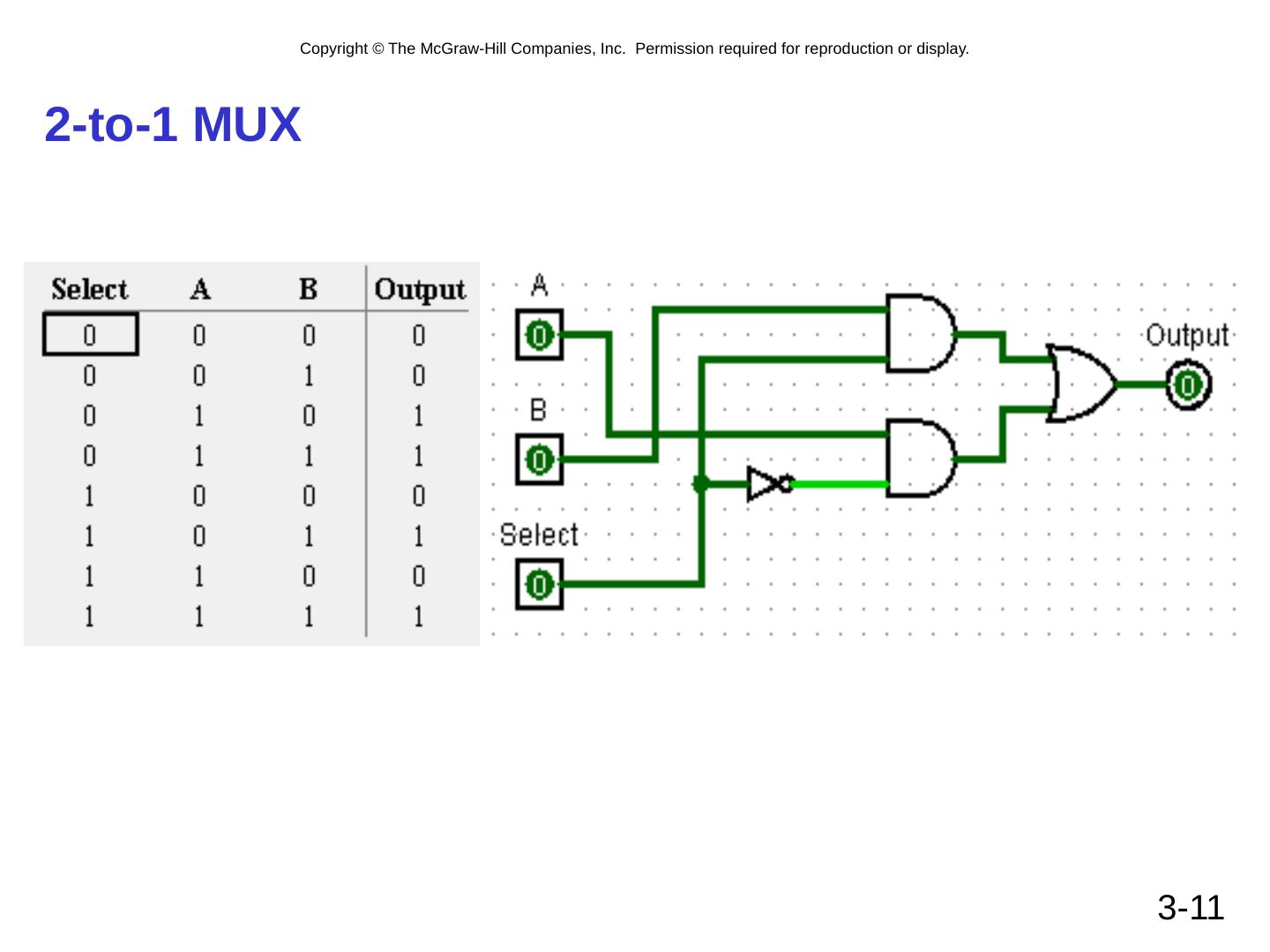
11 .2-to-1 MUX 3- 11
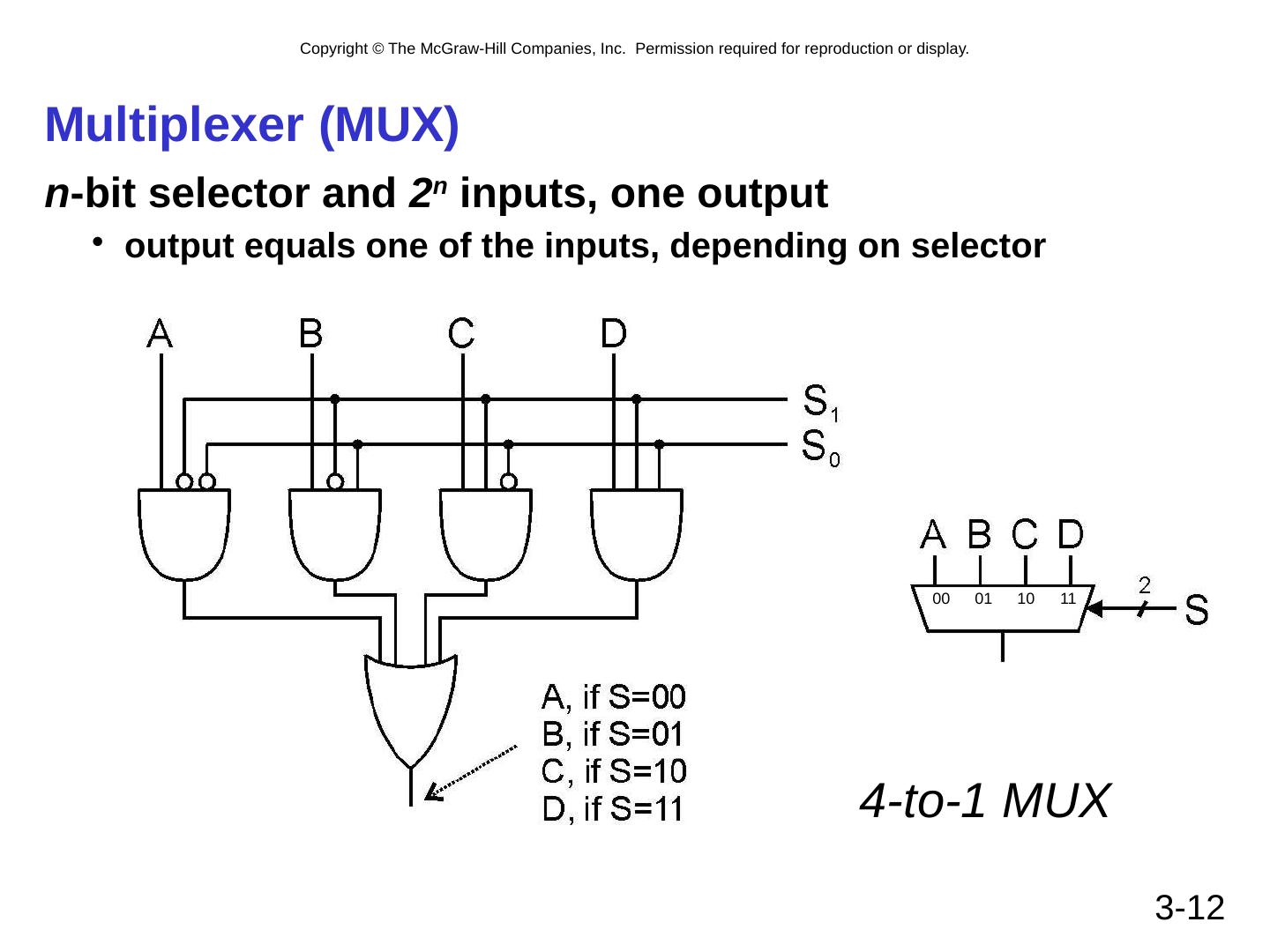
12 .3- 12 Multiplexer (MUX) n -bit selector and 2 n inputs, one output output equals one of the inputs, depending on selector 4-to-1 MUX 00 01 10 11
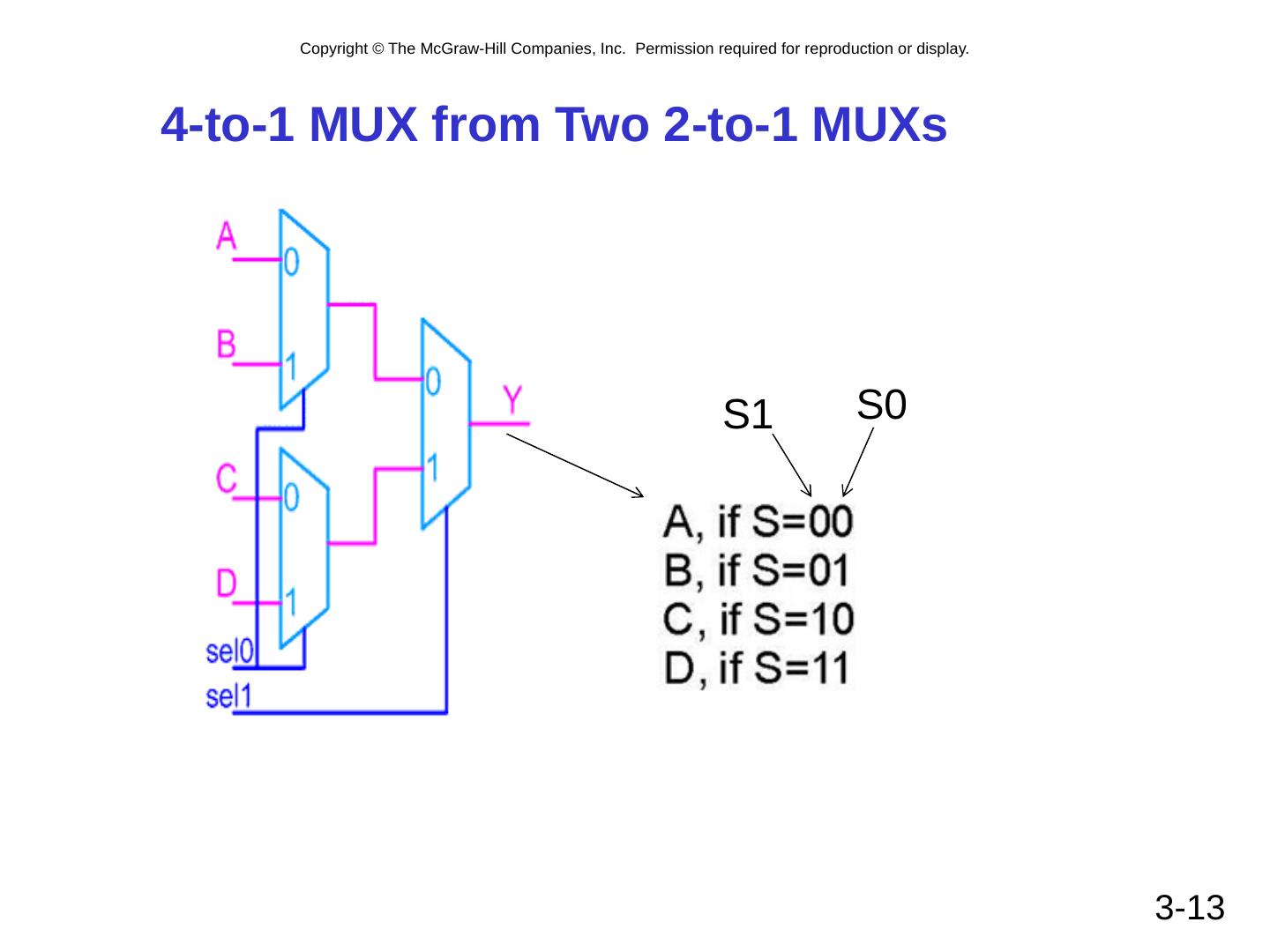
13 .4-to-1 MUX from Two 2-to-1 MUXs 3- 13 S0 S1
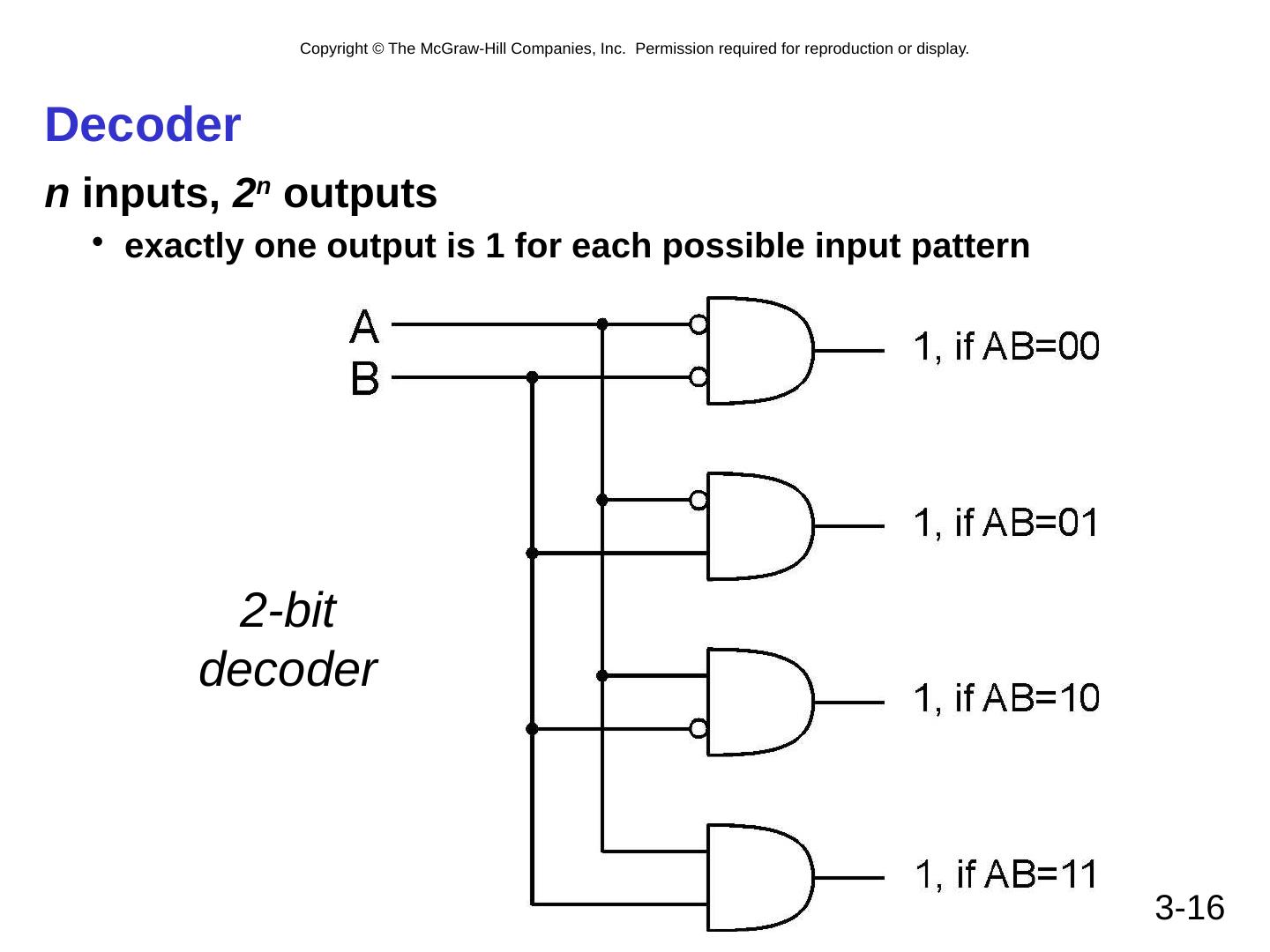
14 .Decoder General example: Assume that some information is encoded in n bits For each encoding, we want to activate the (one) correct output line The general idea: given an n-bit input Detect which of the 2 n combinations is represented Produce 2 n output, only one of which is “1” A n-to-2 n decoder takes an n-bit input and produces 2 n outputs. The n inputs represent a binary number that determines which one of the 2 n outputs is “true” (i.e., 1). 3- 14
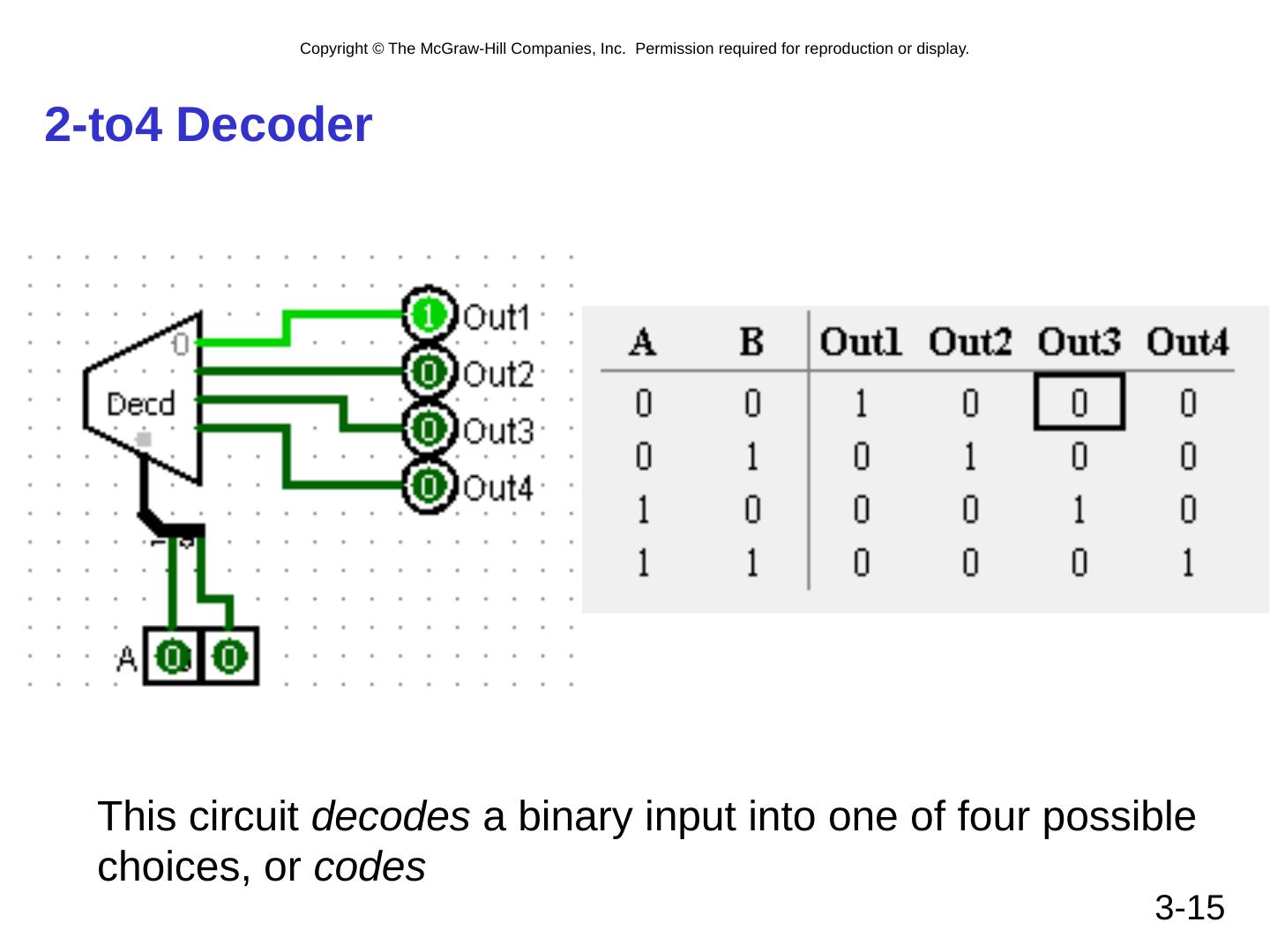
15 .2-to4 Decoder 3- 15 This circuit decodes a binary input into one of four possible choices, or codes
16 .3- 16 Decoder n inputs, 2 n outputs exactly one output is 1 for each possible input pattern 2-bit decoder
17 .3- 17 Representing Multi-bit Values Number bits from right (0) to left (n-1) just a convention -- could be left to right, but must be consistent Use brackets to denote range: D[l:r] denotes bit l to bit r , from left to right May also see A <14:9> , especially in hardware block diagrams. A = 0101001101010101 A[2:0] = 101 A[14:9] = 101001 0 15
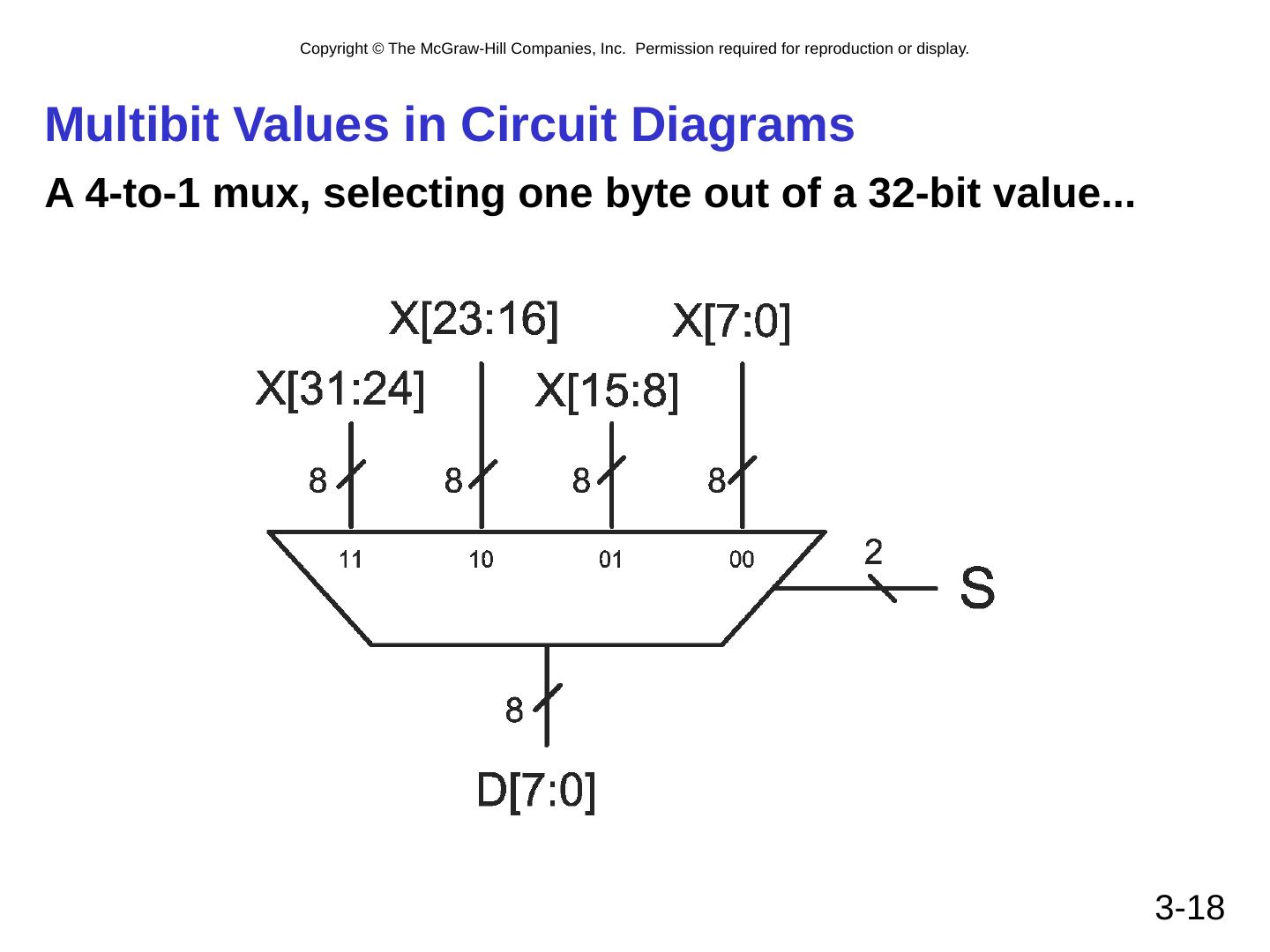
18 .Multibit Values in Circuit Diagrams A 4-to-1 mux , selecting one byte out of a 32-bit value... 3- 18
19 .MUX example -- what does this circuit do? 3- 19
20 .3- 20 Combinational vs. Sequential Combinational Circuit always gives the same output for a given set of inputs ex: adder always generates sum and carry, regardless of previous inputs Sequential Circuit stores information output depends on stored information (state) plus input so a given input might produce different outputs, depending on the stored information example: ticket counter advances when you push the button output depends on previous state useful for building “memory” elements and “state machines”