连续型随机变量

1 . 2-2: 连续型随机变量 张伟平 课件 http://staff.ustc.edu.cn/~zwp/ 论坛 http://fisher.stat.ustc.edu.cn 

2 .第二章随机变量及其分布 2.2 连续型随机变量 . . . . . . . . . . . . . . . . . 1 2.2.1 正态分布 . . . . . . . . . . . . . . . . 11 2.2.2 指数分布 . . . . . . . . . . . . . . . . 16 2.2.3 均匀分布 . . . . . . . . . . . . . . . . 21 Previous Next First Last Back Forward 1 

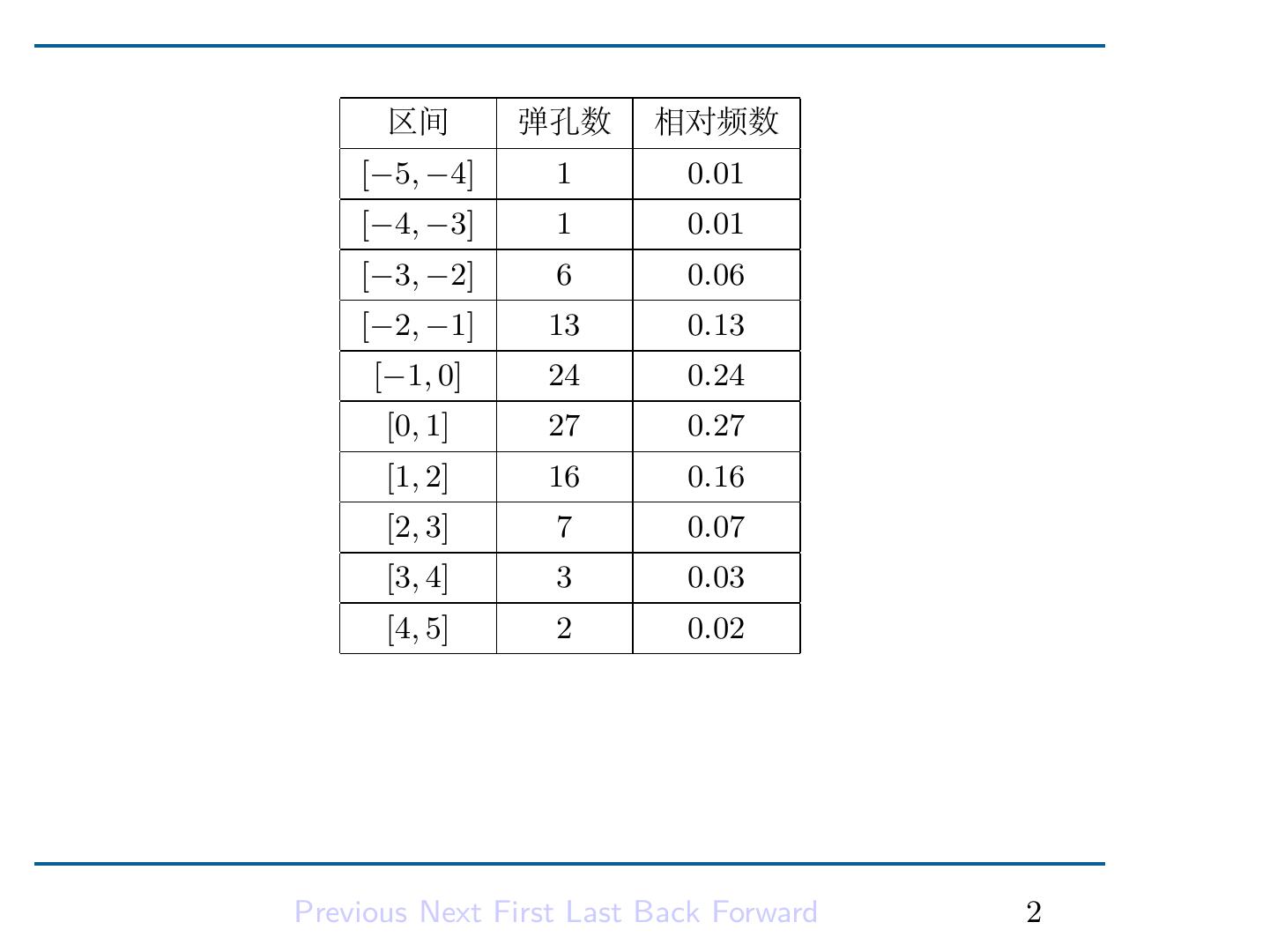
3 . 2.2 连续型随机变量 离散随机变量只取有限个或可数无限个值，而连续型随机变量取 不可数个值. 这就决定了不能用描述离散型随机变量的办法来刻划连 续型随机变量. 考虑一个例子. 假定步枪射手瞄准靶子在固定的位置进行一系 列的射击. 令 X 是命中点与过靶心垂线的水平偏离值，设 X 取值 [−5cm, 5cm]. X 是一个连续随机变量. 为了计算 X 落在某区间的概率，将 [−5, 5] 分为长为 1 厘米的 小区间. 对于每个小区间，以落在这个小区间的弹孔数除以弹孔总数 得到落在这个区间的弹孔的相对频数. 设总弹孔数为 100. 我们得到 下表： Previous Next First Last Back Forward 1 

4 . 区间 弹孔数 相对频数 [−5, −4] 1 0.01 [−4, −3] 1 0.01 [−3, −2] 6 0.06 [−2, −1] 13 0.13 [−1, 0] 24 0.24 [0, 1] 27 0.27 [1, 2] 16 0.16 [2, 3] 7 0.07 [3, 4] 3 0.03 [4, 5] 2 0.02 Previous Next First Last Back Forward 2 

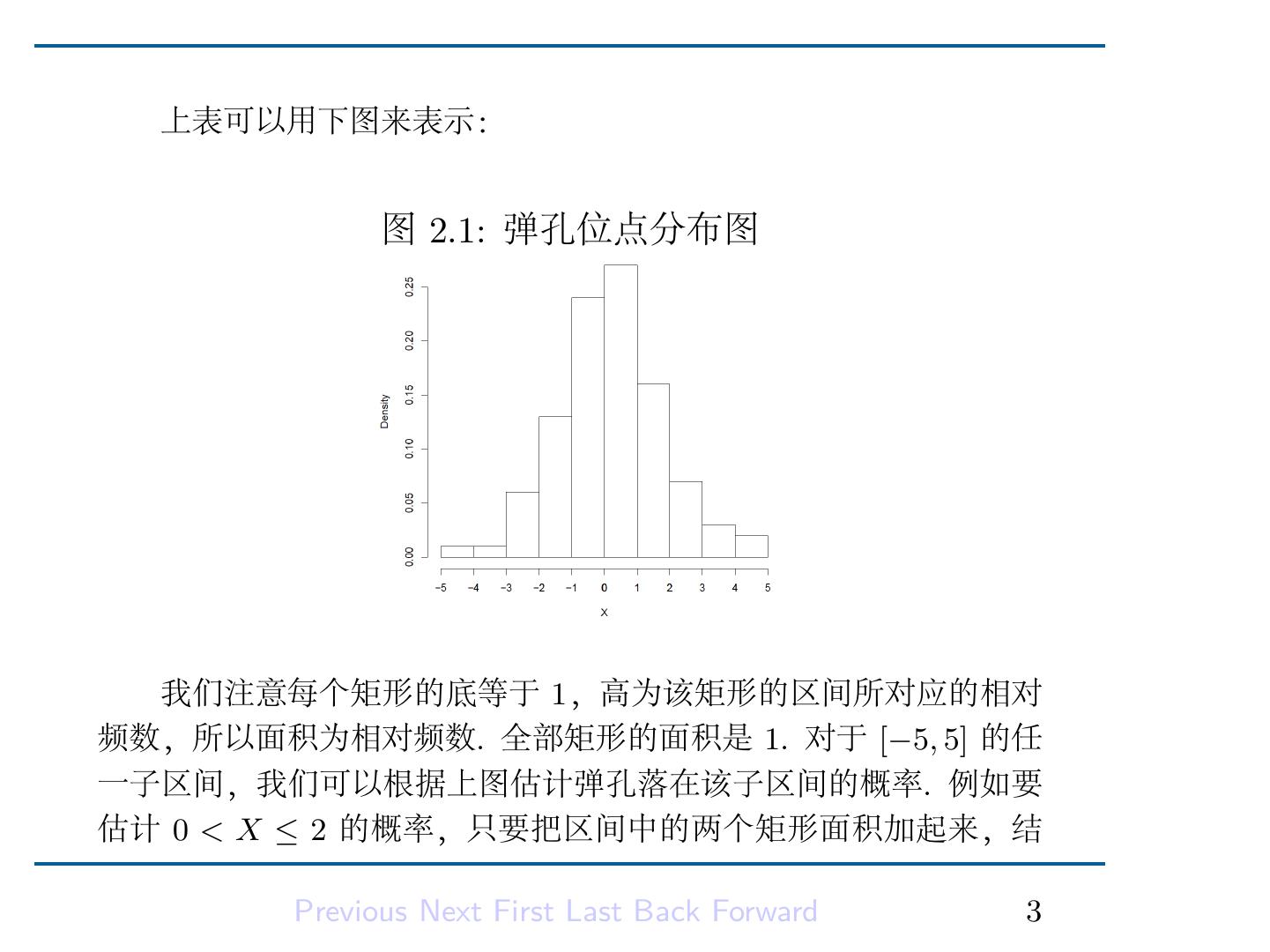
5 . 上表可以用下图来表示： 图 2.1: 弹孔位点分布图 我们注意每个矩形的底等于 1，高为该矩形的区间所对应的相对 频数，所以面积为相对频数. 全部矩形的面积是 1. 对于 [−5, 5] 的任 一子区间，我们可以根据上图估计弹孔落在该子区间的概率. 例如要 估计 0 < X ≤ 2 的概率，只要把区间中的两个矩形面积加起来，结 Previous Next First Last Back Forward 3 

6 .果得到 0.43. 再譬如说要估计 −0.25 < X ≤ 1.5 中的概率，我们应 当计算该区间上的面积，结果得到： 0.06 + 0.27 + 0.08 = 0.41. 如果第二批的 100 颗子弹射在靶子上，我们就将获得另一个经 验分布. 它与第一个经验分布多半是不同的，尽管它们的外表可能相 似. 如果把观察到的相对频数看作为某一 “真” 概率的估计，则我们 假定有一个函数，它将给出任何区间中的精确概率. 这些概率由曲线 下的面积给出. 由此我们得到如下定义： Previous Next First Last Back Forward 4 

7 .X 称为连续型随机变量，如果存在一个函数 f ，叫做 X 的 概率密度函数，它满足下面的条件： 1. 对所有的 −∞ < x < +∞, 有 f (x) ≥ 0; Definition ∫ +∞ 2. −∞ f (x)dx = 1; 3. 对于任意的 −∞ < a ≤ b < +∞, 有 P (a ≤ X ≤ b) = ∫b a f (x)dx. ∫x 注 1. 对于任意的 −∞ < x < +∞, 有 P (X = x) = x f (u)du = 0. Previous Next First Last Back Forward 5 

8 .注 2. 如果 f 只取某有限区间 [a, b] 的值, 令 { f (x) x ∈ [a, b], f˜(x) = 0 其它. 则 f˜ 是定义在 (−∞, +∞) 上的密度函数, 且 f (x) 和 f˜(x) 给出相同 的概率分布. 注 3. 假设有总共一个单位的质量连续地分布在 a ≤ x ≤ b 上. 那么 ∫d f (x) 表示在点 x 的质量密度且 c f (x)dx 表示在区间 [c, d] 上的全 部质量. 由于连续随机变量的概率是用积分给出的, 我们可以直接处理密 度的积分而不是密度本身. Previous Next First Last Back Forward 6 

9 .设 X 为一连续型随机变量. 则 ∫ x F (x) = f (u)du, −∞ < x < +∞ (2.1) Definition −∞ 称为 X 的 (累积) 分布函数. 注 4. F (x) 表示的是随机变量的数值小于或等于 x 的概率, 即 F (x) = P (X ≤ x) − ∞ < x < +∞. (2.2) 由式 (2.2) 定义的 F 为 X 的 (累积) 分布函数的一般定义. 它适用于 任意的随机变量. 设 X 为一离散型随机变量, 它以概率 {p1 , ..., pn , ..} 取值 {a1 , ..., an , ...}. 则 ∑ F (x) = pi . ai ≤x Previous Next First Last Back Forward 7 

10 . 分布函数 F 具有下列性质: (1) F 是非减的函数; 对任何 x1 < x2 都有, F (x2 ) − F (x1 ) = P (x1 < X ≤ x2 ) ≥ 0 (2) 0 ≤ F (x) ≤ 1, x ∈ R, 且 lim F (x) = 0; lim F (x) = 1. x→−∞ x→+∞ (3) F (x) 右连续; Previous Next First Last Back Forward 8 

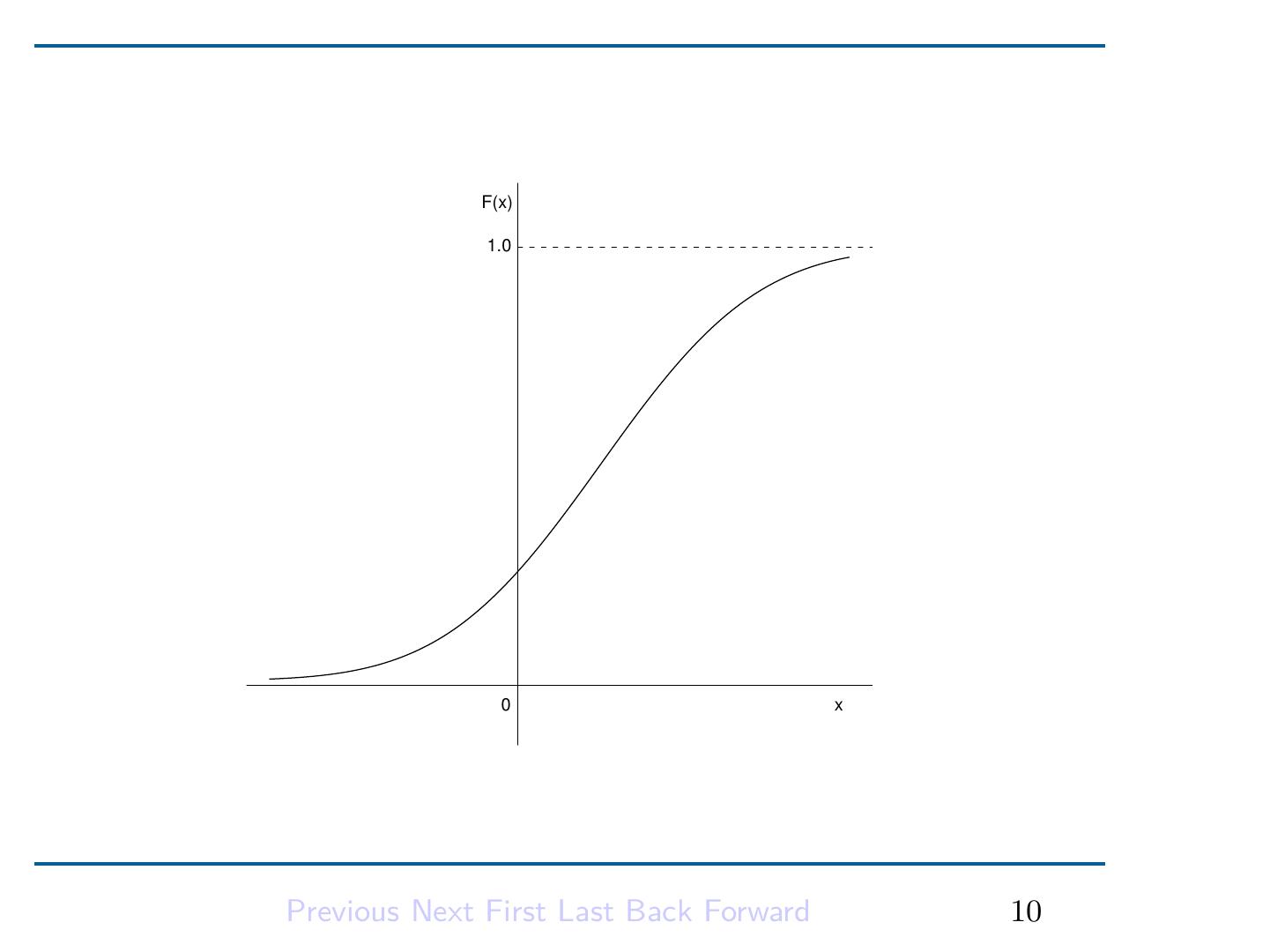
11 . ∑ ∑ F (x) = P (X ≤ x) = P (X = ai ) = pi i:ai ≤x i:ai ≤x 对于连续随机变量, 如果 F (x) 在点 x 的导数存在, 则 f (x) = F ′ (x). 连续随机变量的分布函数的图象如下图所示. Previous Next First Last Back Forward 9 

12 . F(x) 1.0 0 x Previous Next First Last Back Forward 10 

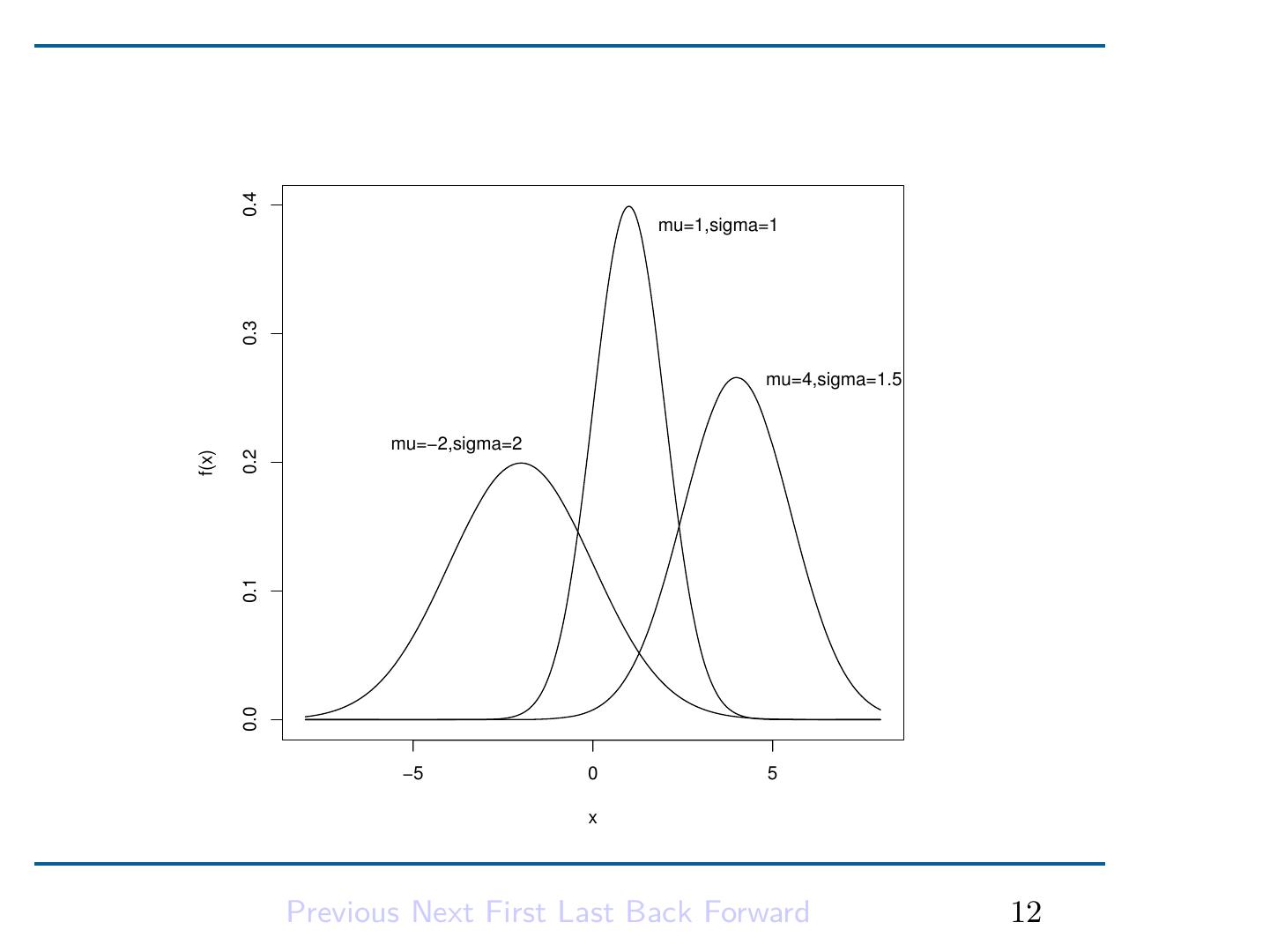
13 . 下面我们介绍常见的连续型分布. 它们包括正态分布, 指数分布 和均匀分布. 2.2.1 正态分布 如果一个随机变量 X 具有概率密度函数 { } 1 (x − µ)2 f (x) = √ exp − , −∞ < x < +∞� (2.3) 2πσ 2σ 2 其中 −∞ < µ < +∞� σ 2 > 0，则称 X 为一正态随机变量，记为 X ∼ N (µ, σ 2 ). 以 (2.3) 为密度的分布称为参数为 µ 和 σ 2 的正态分 布. 具有参数 µ = 0, σ = 1 的正态分布称为标准正态分布. 用 Φ(x) 和 ϕ(x) 表示标准正态分布 N (0, 1) 的分布函数和密度函数. Previous Next First Last Back Forward 11 

14 . 0.4 mu=1,sigma=1 0.3 mu=4,sigma=1.5 mu=−2,sigma=2 0.2 f(x) 0.1 0.0 −5 0 5 x Previous Next First Last Back Forward 12 

15 .in R ↑Code x <- seq(-4, 4, length = 401) plot(x, dnorm(x), type = 'l') # N(0, 1) N(1, 1.52 ): lines(x, dnorm(x, mean = 1, sd = 1.5), lty = 'dashed') ↓Code 从上图可以看出, 正态分布的密度函数是以 x = µ 为对称轴的 对称函数. µ 称为位置参数. 密度函数在 x = µ 处达到最大值，在 (−∞, µ) 和 (µ, +∞) 内严格单调. 同时我们看到, σ 的大小决定了密 度函数的陡峭程度. 通常称 σ 为正态分布的形状参数. 以 F (x) 记正态分布 N (µ, σ 2 ) 的概率分布函数，则恒有 F (x) = Φ( x−µ σ ). 所以任一正态分布的概率分布函数都可通过标准正态分布 的分布函数计算出来. Previous Next First Last Back Forward 13 

16 . ↑Example 设 X ∼ N (µ, σ 2 ), 则 X−µ σ ∼ N (0, 1). ↓Example 证: 由 (X − µ ) P ≤ x = P (X ≤ σx + µ) σ ∫ σx+µ 1 2 2 = √ e−(t−µ) /(2σ ) dt −∞ 2πσ ∫ x 1 2 √ e−z /2 dz t=σz+µ = −∞ 2π Previous Next First Last Back Forward 14 

17 . ↑Example 求数 k 使得对于正态分布的变量有 P (µ − kσ < x < µ + kσ) = 0.95. ↓Example 解: 令 F 为正态分布 N (µ, σ 2 ) 的分布函数, 则有 P (µ − kσ < x < µ + kσ) = F (µ + kσ) − F (µ − kσ) = Φ(k) − Φ(−k) = 0.95. (2.4) 从关系式 Φ(−k) = 1 − Φ(k), 我们得 2Φ(k) − 1 = 0.95. 所以 Φ(k) = 0.975. 查正态分布表, 得 k = 1.96. Previous Next First Last Back Forward 15 

18 .2.2.2 指数分布 若随机变量 X 具有概率密度函数 { λe−λx x > 0, f (x) = (2.5) 0 x ≤ 0, 其中 λ > 0 为常数, 则称 X 服从参数为 λ 的指数分布. 指数分布的分布函数为 { 1 − e−λx x > 0, F (x) = (2.6) 0 x ≤ 0. Previous Next First Last Back Forward 16 

19 . 0.5 0.4 lambda=1 0.3 f(x) 0.2 0.1 lambda=0.5 0.0 lambda=3 0 2 4 6 8 10 x Previous Next First Last Back Forward 17 

20 . in R ↑Code dexp, rexp, pexp, qexp ↓Code 从图 (2.5) 可以看出, 参数 λ 愈大, 密度函数下降得愈快. 指数分布经常用于作为各种” 寿命” 的分布的近似. 令 X 表示某 元件的寿命. 我们引进 X 的失效率函数如下: P (x ≤ X ≤ x + ∆x|X > x) h(x) = lim . ∆x→0 ∆x 失效率表示了元件在时刻 x 尚能正常工作, 在时刻 x 以后, 单位时间 内发生失效的概率. 则如果 h(x) ≡ λ (常数), 0 < x < +∞, X 服从指数分布. 即指数分布描述了无老化时的寿命分布. Previous Next First Last Back Forward 18 

21 . ↑Example 设 X 表示某种电子元件的寿命，F (x) 为其分布函数。若假设元 件无老化，即元件在时刻 x 正常工作的条件下，其失效率保持为某 个常数 λ，与 x 无关。试证明 X 服从指数分布。 ↓Example 解：失效率即单位时间内失效的概率，因此由题设知 P (x ≤ X ≤ x + h|X > x)/h = λ, h→0 因为 P ({x ≤ X ≤ x + h}{X > x}) F (x + h) − F (x) P (x ≤ X ≤ x+h|X > x) = = P (X > x) 1 − F (x) 所以有 F ′ (x) lim P (x ≤ X ≤ x + h|X > x)/h = =λ h→0 1 − F (x) F ′ (x) 即得到微分方程 1−F (x) = λ, 解此方程得到 F (x) = 1 − e−λx Previous Next First Last Back Forward 19 

22 .从而结论得证。 指数分布的最重要的特点是 “无记忆性”. 即若 X 服从指数分布， 则对任意的 s, t > 0 有 P (X > s + t | X > s) = P (X > t). (2.7) 即寿命是无老化的. 可以证明, 指数分布是唯一具有性质 (2.7) 的连 续型分布. Previous Next First Last Back Forward 20 

23 .2.2.3 均匀分布 设 −∞ < a < b < +∞，如果随机变量 X 具有密度函数 { 1 b−a a≤x≤b, f (x) = (2.8) 0 其它, 则称该随机变量为区间 [a, b] 上的均匀分布, 记作 U [a, b]. 如此定义 的 f (x) 显然是一个概率密度函数. 容易算出其相应的分布函数为    x ≤ a,  0, F (x) = x−a , a < x ≤ b,   b−a  1, x > b. in R ↑Code dunif, runif, punif, qunif ↓Code Previous Next First Last Back Forward 21 

24 .在计算时因四舍五入而产生的误差可以用均匀分布来描述. Previous Next First Last Back Forward 22