条件概率与独立性

下载 1

enough

发布于

2465

人观看

#信息技术

本章主要讲述了条件概率与独立性的概念性质。通过例题学习了全概率公式和Bayes 公式的运用。介绍了事件的独立性，即设A,B 是随机试验中的两个事件, 若满足P(AB) =P(A)P(B) , 则称事件A 和B 相互独立。

展开查看详情

1 . 1.3: 条件概率与独立性张伟平课件 http://staff.ustc.edu.cn/~zwp/ 论坛 http://fisher.stat.ustc.edu.cn

2 .第一章事件与概率 1.5 条件概率 . . . . . . . . . . . . . . . . . . . . 2 1.5.1 全概率公式和 Bayes 公式 . . . . . . . 10 1.5.2 事件的独立性 . . . . . . . . . . . . . . 20 Previous Next First Last Back Forward 1

3 .1.5 条件概率 1. 条件概率的定义一般讲, 条件概率就是在知道了一定的信息下所得到的随机事件的概率. 如两个工厂 A 和 B 生产同一品牌的电视机, 商场中该品牌有个统一的次品率, 比如 0.5%, 如果你从某个途径知道该商场的这批电视机是 A 厂生产的, 则你买到的电视机的次品率不再是 0.5%, 这个概率就是条件概率. 设事件 A 和 B 是随机试验 Ω 中的两个事件, P (B) > 0 , 称 P (AB) Deﬁnition P (A|B) = P (B) 为事件 B 发生条件下事件 A 发生的条件概率. Previous Next First Last Back Forward 2

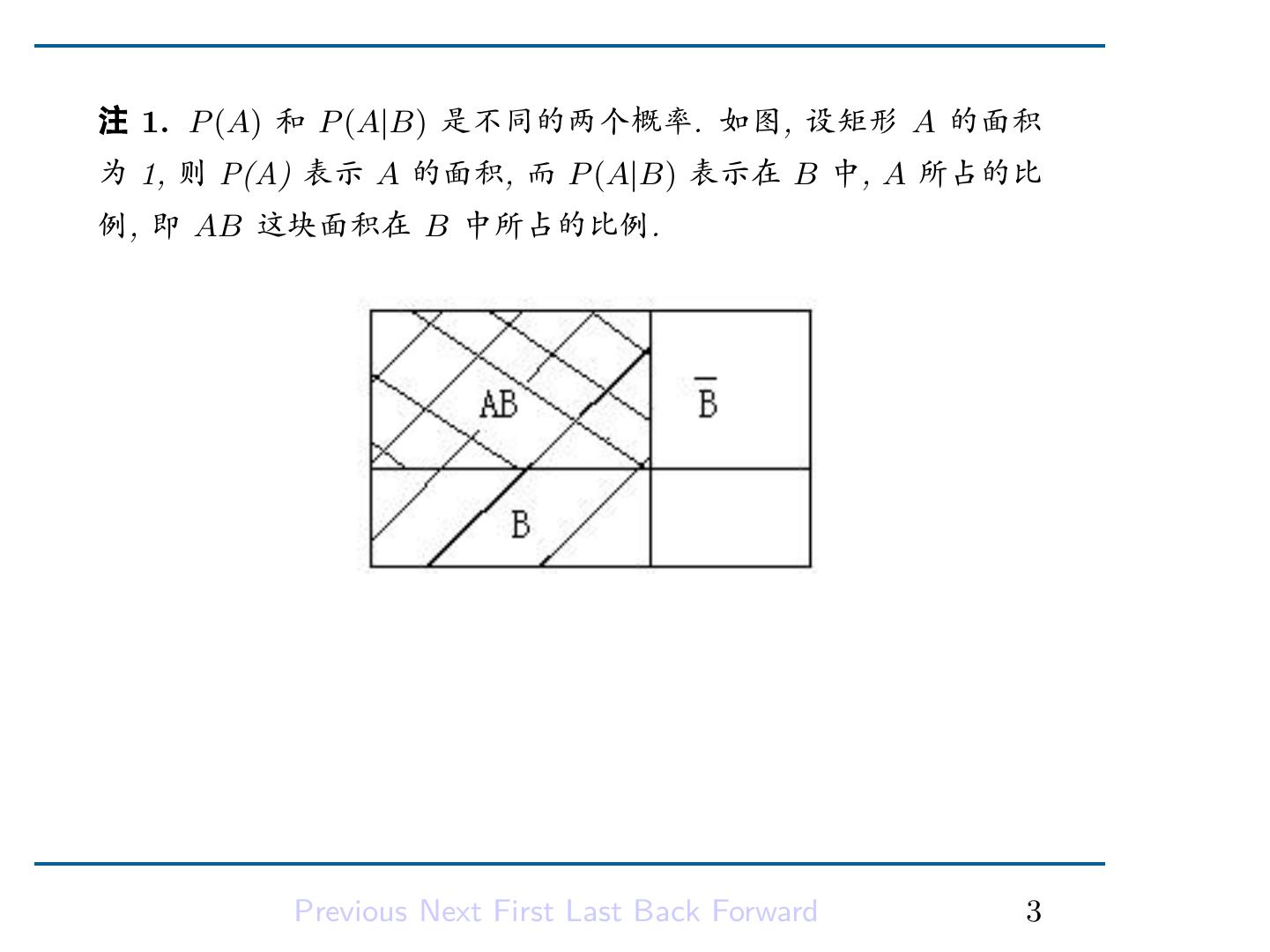
4 .注 1. P (A) 和 P (A|B) 是不同的两个概率. 如图, 设矩形 A 的面积为 1, 则 P(A) 表示 A 的面积, 而 P (A|B) 表示在 B 中, A 所占的比例, 即 AB 这块面积在 B 中所占的比例. Previous Next First Last Back Forward 3

5 .注 2. 可以从概率的统计定义, 即用频率来近似概率这一角度来理解条件概率. 设在 n 次独立试验中, 事件 A 发生了 nA 次, 事件 B 发生了 nB 次, 事件 AB 发生了 nAB 次, 事件 B 发生下事件 A 发生的频率为 nAB P (AB) ≈ nB P (B) 注 3. 事实上, 我们所考虑的概率都是在一定条件下计算的, 因为随机试验就是在一定的条件下进行的, 所以样本空间是相对而言的. 如果把在一定条件下的随机试验看成无条件的, 则在补充条件下进行的随机试验的结果一般而言相对于原有结果要少, 即样本空间改变了. 所以所得随机事件的概率一般是不相同的. Previous Next First Last Back Forward 4

6 . ↑Example 有 10 个产品, 内有 3 个次品, 从中一个个地抽取 (不放回) 检验, 问第一次取到次品后第二次再取到次品的概率. ↓Example 解: 样本空间 Ω 是从 10 个产品中有序取出 2 个产品的不同方法, 这是一个排列问题, 易知 |Ω| = 10 × 9 = 90, 记 A ={第一次取出的是次品}, B ={第二次取出的是次品}, |AB| = 6, |A| = 3, 故 P (AB) 6/90 P (B|A) = = = 2/9 P (A) 3/10 注意, P (B|A) = 2/9 ̸= P (A) = 3/10. Previous Next First Last Back Forward 5

7 .2. 乘法定理由 P (A|B) = P (AB) P (B) ⇒ P (AB) = P (A|B)P (B) 由归纳法容易推广为 n 个事件同时发生的概率有如下公式: P (A1 A2 · · · An ) = P (A1 )P (A2 |A1 ) · · · P (An |A1 · · · An−1 ) 上面公式的右边看似麻烦, 其实在实际中很容易算出. 在没有给出 n 个事件之间相互关系时, 这是计算 n 个事件同时发生的一个重要公式. Previous Next First Last Back Forward 6

8 . ↑Example 某人忘了某饭店电话号码的最后一个数字, 因而随意拨号, 问他三次之内拨通电话的概率. ↓Example 解:令 Ai ={第 i 次打通电话}, i = 1, 2, 3 , 则 P (3次内拨通电话) = P (A1 ∪ A2 ∪ A3 ) = 1 − P (A¯1 A¯2 A¯3 ) 9 87 = 1− = 0.3 10 9 8 Previous Next First Last Back Forward 7

9 . ↑Example 将 n 根短绳的 2n 个端头任意两两连接, 试求恰好连成 n 个圈的概率. ↓Example 解: 以 Ω 表示所有不同连结结果的集合, 设想把 2n 个端头排成一行, 然后规定将第 2k−1 个端头与第 2k 个端头相连接,k = 1, 2, · · · , n. 于是每一种排法对应一种连结结果, 从而 |Ω| = (2n)!. 以 A 表示恰好连成 n 个圈的事件. 设想已将 n 根短绳作了编号, 以 Ak 表示第 k 号 ∩ n 短绳被连成 1 个圈的事件, 于是有 A = Ak . k=1 当 A1 发生时,1 号短绳被连成 1 个圈, 这相当于有一个 k ∈ {1, 2, · · · , n}, 使得在 2n 个端头的排列中,1 号短绳的两个端头排在第 2k − 1 和第 2k 个位置上, 所以 |A1 | = 2n(2n − 2)!. 因此 |A1 | 1 P (A1 ) = = . |Ω| 2n − 1 Previous Next First Last Back Forward 8

10 .我们来求 P (A2 |A1 ), 即要在已知 1 号短绳被连成 1 个圈的情况下, 求 2 号短绳也被连成 1 个圈的概率. 既然 1 号短绳已经自成 1 个圈, 我们就可以不考虑它, 只要对剩下的 n − 1 根短绳讨论其中的头一号短绳被连成 1 个圈的问题就行了. 即知 1 1 P (A2 |A1 ) = = . 2(n − 1) − 1 2n − 3 同理可得 1 1 P (Ak |A1 A2 · · · Ak−1 ) = = , k = 3, 4, · · · , n. 2[n − (k − 1)] − 1 2n − 2k + 1 于是由概率乘法定理中的 (2.3.6) 式得到 ∩ n ∏ n 1 1 P (A) = P ( Ak ) = = . 2n − 2k + 1 (2n − 1)!! k=1 k=1 在这个解法中, 充分体现了利用变化了的概率空间计算条件概率的好处. Previous Next First Last Back Forward 9

11 .1.5.1 全概率公式和 Bayes 公式 1. 全概率公式设 B1 , B2 , · · · Bn 是样本空间 Ω 中的两两不相容的一组事 ∪n 件, 即 Bi Bj = ϕ, i ̸= j, 且满足 i=1 Bi = Ω, 则称 Deﬁnition B1 , B2 , · · · Bn 是样本空间 Ω 的一个分割. 全概率公式: 设 {B1 , B2 , · · · Bn } 是样本空间 Ω 的一个分割, 且 P (Bi ) > 0(i = 1, · · · , n), A 为 Ω 中的一个事件, 则 ∑ n P (A) = P (A|Bi )P (Bi ) i=1 Previous Next First Last Back Forward 10

12 . ↑Example 设某厂产品的一个零部件是由三家上游厂商供货的. 已知有一半是 B1 厂提供的, B2 厂商和 B3 分别提供 25% . 已知厂商 B1 和 B2 的次品率都是 2%, B3 的次品率为 4%, 从该厂产品中任取一个产品, 问该产品的这个零部件是次品的概率. ↓Example 解:记 A ={取出的产品为次品}, Bi ={取到的产品是 Bi 厂生产的}, i = 1, 2, 3. 易见 B1 , B2 , B3 构成样本空间的一个分割, 且 P (B1 ) = 0.5, P (B2 ) = P (B3 ) = 0.25, P (A|B1 ) = P (A|B2 ) = 0.02, P (A|B3 ) = 0.04, 从而由全概率公式马上得到 P (A) = 0.02 × 0.5 + 0.02 × 0.25 + 0.04 × 0.25 = 0.025. Previous Next First Last Back Forward 11

13 . ↑Example 将 n 根短绳的 2n 个端头任意两两连接, 求恰好连成 n 个圈的概率. ↓Example 解:现在再来利用全概率公式给出一个解答. 以 An 表示 n 根短绳恰好连成 n 个圈的事件, 记 pn = P (An ). 再以 B 表示第 1 根短绳连成 1 个圈的事件, 用 B 和 B c 作为对 Ω 的一个分划. 于是由全概率公式得 pn = P (An ) = P (B)P (An |B) + P (B c )P (An |B c ). 在前面例子中已经求得 P (B) = 1 2n−1 ; 易见 P (An |B c ) = 0; 而 P (An |B) 则是在已知第 1 根短绳连成 1 个圈的条件下, 其余 n − 1 根短绳连成 n − 1 个圈的概率, 此时第 1 根短绳已经与其余 n − 1 根短绳无关, 所以 P (An |B) = P (An−1 ) = pn−1 , 代入上式即可得到 1 pn = P (An ) = pn−1 , n = 2, 3, · · · . 2n − 1 Previous Next First Last Back Forward 12

14 .反复利用该式, 并注意 p1 = 1, 即得 1 pn = , n = 1, 2, · · · . (2n − 1)!! Previous Next First Last Back Forward 13

15 . ↑Example ( Polya 罐子模型) 罐中放有 a 个白球和 b 个黑球, 每次从罐中随机抽取一个球, 并连同 c 个同色球一起放回罐中, 如此反复进行. 试证明: 在第 n 次取球时取出白球的概率为 a a+b . ↓Example 证: 以 Ak 表示在第 k 次取球时取出白球的事件, 于是 Ack 就是在第 k 次取球时取出黑球的事件. 我们来对 n 作归纳. 显然有 P (A1 ) = a a+b . 假设 n = k −1, k ≥ 2 时结论成立, 要证 n = k 时结论也成立. 我们以 A1 和 Ac1 作为对 Ω 的一个分划. 注意此时可将 P (Ak |A1 ) 看成是从原来放有 a + c 个白球和 b 个黑球的罐中按规则取球, 并且在第 k − 1 次取球时取出白球的概率, 因此由归纳假设知 P (Ak |A1 ) = a+c a+b+c , 同理亦有 P (Ak |Ac1 ) = a a+b+c , 于是由全概率公式得 P (Ak ) = P (A1 )P (Ak |A1 ) + P (Ac1 )P (Ak |Ac1 ) a a+c b a a = + = . a+b a+b+c a+b+c a+b+c a+b Previous Next First Last Back Forward 14

16 .因此结论对一切 n 成立. Previous Next First Last Back Forward 15

17 . ↑Example 一罐内有 a 个黑球和 b 个白球，从中任意取一球，如果是白球则将它放回去，如果是黑球，则从另一罐内取一白球替换它放回去。在重复 n 次这样的做法后，求第 n+1 次取出的是白球的概率。 ↓Example 解: 记 A={第 n 次取出的是白球}，pn = P (A)，B 为所求事件。则 pn+1 = ¯ (A) P (B) = P (B|A)P (A) + P (B|A)P ¯ 1 = pn ∗ pn + (pn + )(1 − pn ) a+b ( 1 ) 1 = 1− pn + a+b a+b 结合初值 p1 = a a+b ，得到 ( 1 )n b pn+1 = 1 − 1 − . a+b a+b Previous Next First Last Back Forward 16

18 .2. Bayes 公式设 {B1 , B2 , · · · Bn } 是样本空间的一个分割, A 为 Ω 中的一个事件, P (Bi ) > 0, i = 1, 2, · · · , n, P (A) > 0, 则 P (A|Bi )P (Bi ) P (Bi |A) = ∑n j=1 P (A|Bj )P (Bj ) 什么情况下用 Bayes 公式? 由公式知, 分母就是事件 A 的概率, 而分子和等式左边的条件概率中的条件正好反过来. 所以我们知道在因果关系互换时必须用 Bayes 公式. Previous Next First Last Back Forward 17

19 . ↑Example 一种诊断某癌症的试剂, 经临床试验有如下记录: 有癌症病人阳性的概率为 95%, 无癌症病人阴性的概率为 95%. 现用这种试剂在某社区进行癌症普查, 设该社区癌症发病率为 0.5%, 问某人反应为阳性时该人患癌症的概率. ↓Example 解:设 A ={反应为阳性}, C ={被诊断者患癌症}, 由题意, ¯ C) P (A|C) = 0.95, P (A| ¯ = 0.95, P (C) = 0.005, 现在要算的是 P (C|A) . 这是典型的因果关系互换, 只能用 Bayes 公式. Previous Next First Last Back Forward 18

21 .1.5.2 事件的独立性为了计算两个事件同时发生的概率, 可以运用乘法定理, P (AB) = P (A|B)P (B). 什么情况下 P (AB) = P (A)P (B)? 或者等价地， P (A|B) = P (A)? 即 AB 同时发生的概率等于两个事件单独发生概率的乘积? 为此我们有如下的定义: 设 A, B 是随机试验中的两个事件, 若满足 P (AB) = Deﬁnition P (A)P (B) , 则称事件 A 和 B 相互独立. 关于独立的概念, 应该是从实际出发, 如果能够判断事件 B 的发生与否对事件 A 的发生与否不产生影响, 则事件 A, B 即为独立. 如把一个硬币掷两次, 观测正反面出现的情况, A ={第一次出现正面}, B ={第二次出现正面}, AB ={两次都出现正面}, 样本空间 Ω 有 4 Previous Next First Last Back Forward 20

22 .个基本事件, #(AB) = 1, #(A) = 2, #(B) = 2, 故 P (AB) = 1/4, P (A)P (B) = 1/2 · 1/2 = 1/4 即事件 A, B 相互独立. 事实上, 我们容易判断第一次是否出现正面与第二次是否出现正面没有任何影响, 即独立的. 设 A˜ 表示事件 A ˜ 表示事件 B 发生和不发生之一. 由独立性的定发生和不发生之一, B 义可以推知 P (A˜B) ˜ = P (A)P ˜ (B), ˜ (这儿一共 4 个等式) . Previous Next First Last Back Forward 21

23 . 独立性的定义可以推广到 n 个事件. 设 A1 , A2 , · · · An 是随机试验中的 n 个事件, 以 A˜i 表示 Ai 或 A¯i 之一. 若满足 Deﬁnition P (A˜1 A˜2 · · · A˜n ) = P (A˜1 )P (A˜2 ) · · · P (A˜n ), 则称事件列 A1 , A2 , · · · An 相互独立. (上面有 2n 个等式) 注意: 上面等式等价于对 A1 , A2 , · · · An 中的任意 k 个事件 Ai1 , Ai2 , · · · , Aik , k = 2, · · · n, 有 P (Ai1 Ai2 · · · Aik ) = P (Ai1 )P (Ai2 ) · · · P (Aik ) 若 A1 , · · · , An 中任意两个事件相互独立, 则称为两两独立. 注意: 独立和不相容是不同的两个概念. Previous Next First Last Back Forward 22

24 . ↑Example (两两独立而不相互独立的反例) 有四个同样的小球, 分别在其上写上“1”，“2”，“3”和“1,2,3”。引进三个事件: Ai ={随机取一球，球上有数字 i}, i = 1, 2, 3. 试讨论事件 A1 , A2 , A3 是否相互独立. ↓Example 解:易知 P (A1 ) = P (A2 ) = P (A3 ) = 1 2 , P (A1 A2 ) = P (A2 A3 ) = P (A3 A1 ) = 1 4 , 但是却有 P (A1 A2 A3 ) = 41 ̸= P (A1 )P (A2 )P (A3 ), 所以事件 A1 , A2 , A3 两两独立, 但不相互独立. 这个例子说明两两独立不一定独立。 Previous Next First Last Back Forward 23

25 . ↑Example A, B, C 三人独立地破译密码, 每人能破译密码的概率分别为 1/3, 1/4, 1/5. 问密码能被破译的概率有多大? ↓Example 解: 设 D={密码被破译}, A, B 和 C 分别表示 A, B 和 C 三人能破译密码这三个事件, 由独立性, P (D) = P (A ∪ B ∪ C) = 1 − P (A¯B ¯ C) ¯ = 1 − P (A)P ¯ (B)P ¯ (C)¯ = 1 − 2 3 4 = 0.6 345 Previous Next First Last Back Forward 24

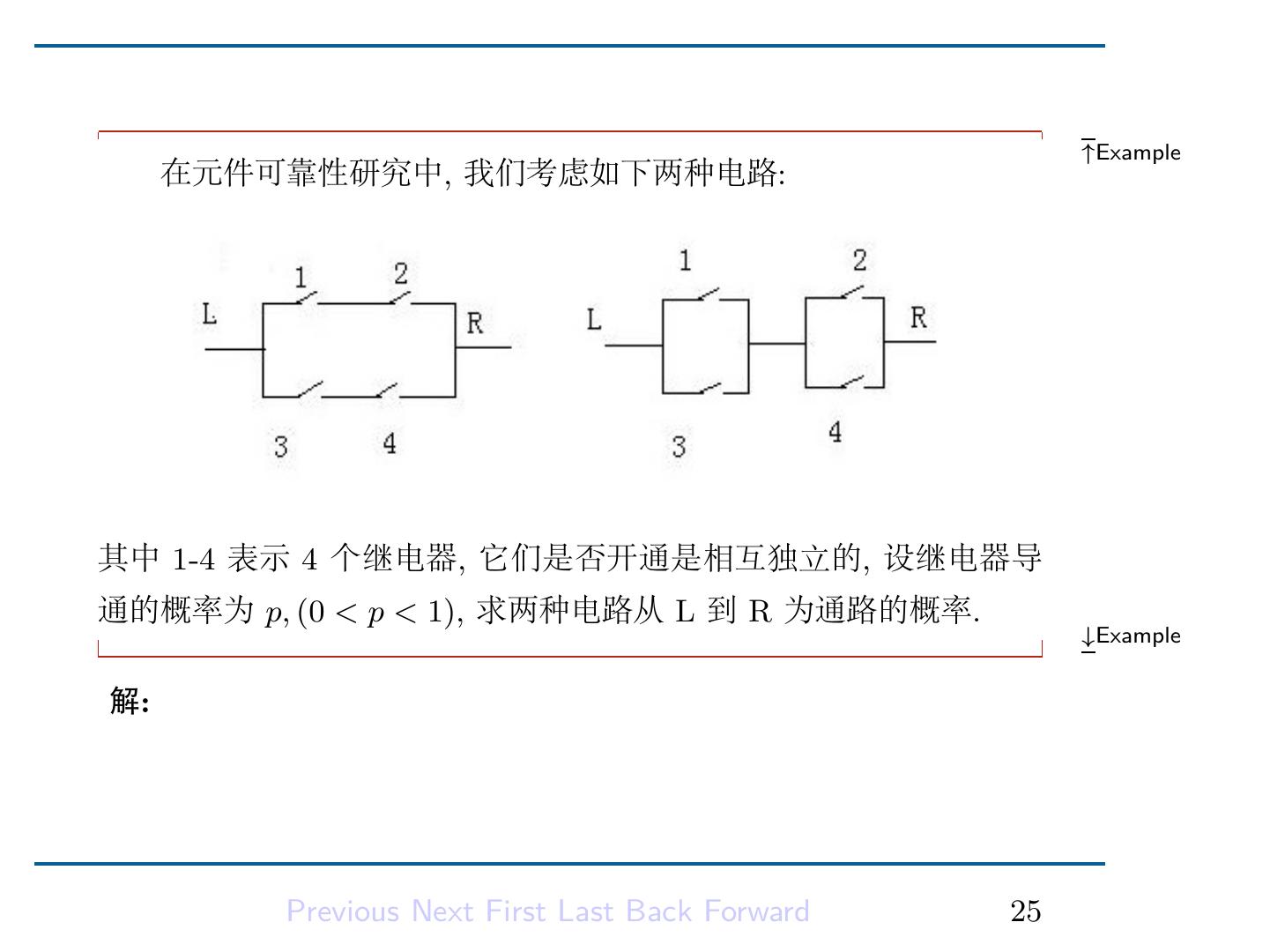
26 . ↑Example 在元件可靠性研究中, 我们考虑如下两种电路: 其中 1-4 表示 4 个继电器, 它们是否开通是相互独立的, 设继电器导通的概率为 p, (0 < p < 1), 求两种电路从 L 到 R 为通路的概率. ↓Example 解: 左图为串联后并联, 右边为并联后串联, 记 Ai ={第 i 个继电器导通}, 则左图 LR 为通路的表达为 A1 A2 ∪ A3 A4 , 右图 LR 为通路的表达为 (A1 ∪ A3 ) ∩ (A2 ∪ A4 ), Previous Next First Last Back Forward 25

27 . 由于 P (A1 A2 ) = P (A1 )P (A2 ) = p2 = P (A3 A4 ), 故 P (A1 A2 ∪ A3 A4 ) = p2 + p2 − p4 = p2 (2 − p2 ) 同理, P ((A1 ∪ A3 ) ∩ (A2 ∪ A4 )) = (2p − p2 )2 = p2 (2 − p)2 , 由于 2 − p2 < (2 − p)2 , 故并联后串联的电路比串联后并联的电路的可靠性高一点. Previous Next First Last Back Forward 26

28 . ↑Example 假设某个人独立向同一目标射击 n 次, 每次命中目标的概率为 p(p < 0.05), 求他在 n 次射击中至少有一次命中目标的概率. ↓Example 解:令 Ai ={第 i 次命中目标}, D ={至少有一次命中目标}, 则 ∪ n D = Ai , i=1 P (D) = 1 − P (D) ¯ = 1 − P (A¯1 A¯2 · · · A¯n ) = 1 − (1 − p)(1 − p) · · · (1 − p) ≈ 1 − exp{−np} 上面约等号在 p 较小时成立. 例如 p = 0.04, n = 100 时, P (D) ≈ 1−exp{−4} = 0.98168. Previous Next First Last Back Forward 27

29 . 小概率原理一个事件如果发生的概率很小的话，那么它在一次试验中是几乎不可能发生的，但在多次重复试验中几乎是必然发生的，数学上称之小概率原理。 ↑Example 某停车场有 16 个并排的车位, 有天发现有 12 个车位停了车, 4 个相连的车位还空着. 由此能得出什么结论? ↓Example • 购买彩票 • 乘坐飞机 • ... Previous Next First Last Back Forward 28

2点赞

1收藏

1下载