展开查看详情
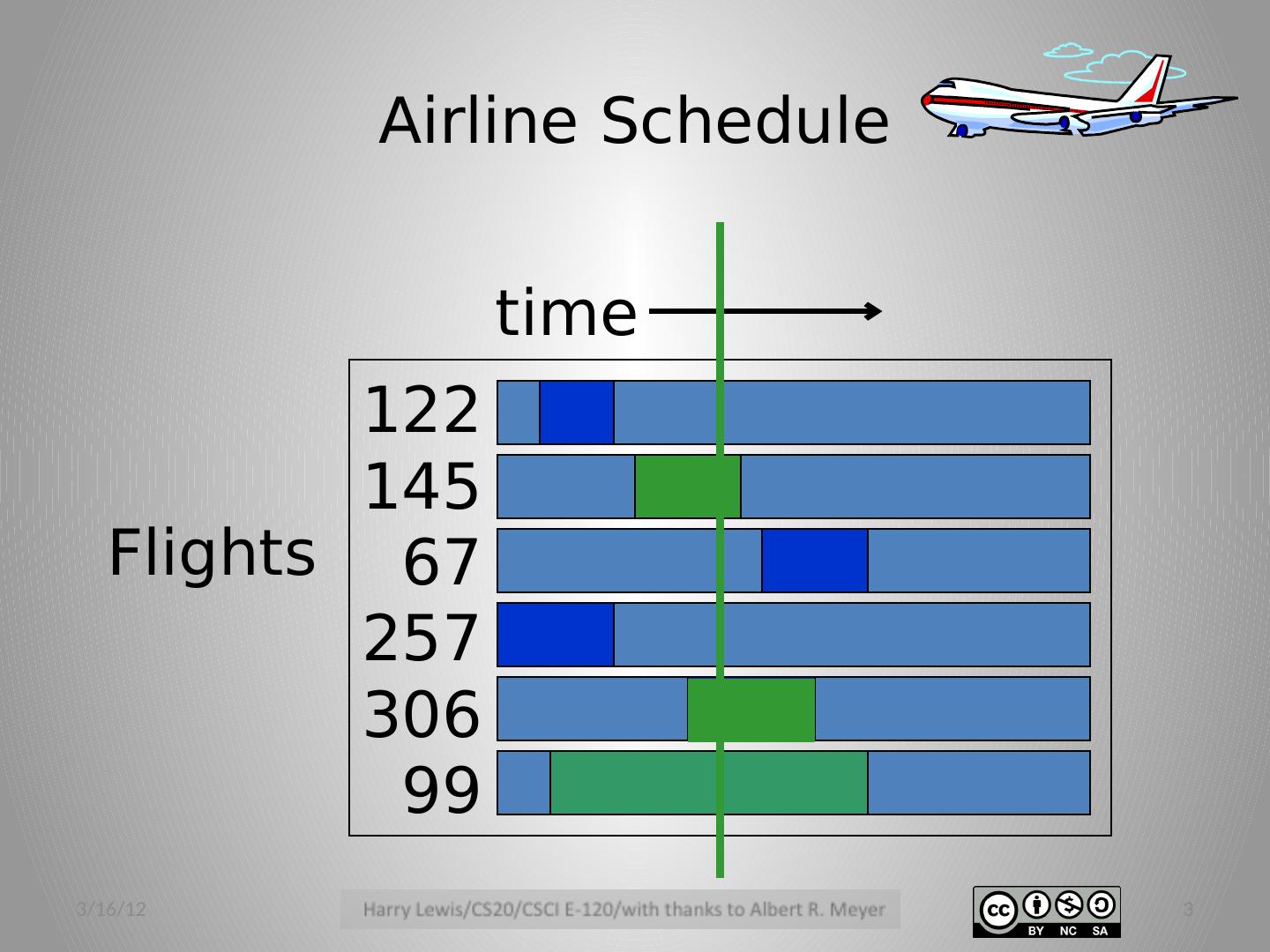
2 .Flight Gates flights need gates, but times overlap. how many gates needed? 3/16/12 2
3 .Airline Schedule 122 145 67 257 306 99 Flights time 3/16/12 3
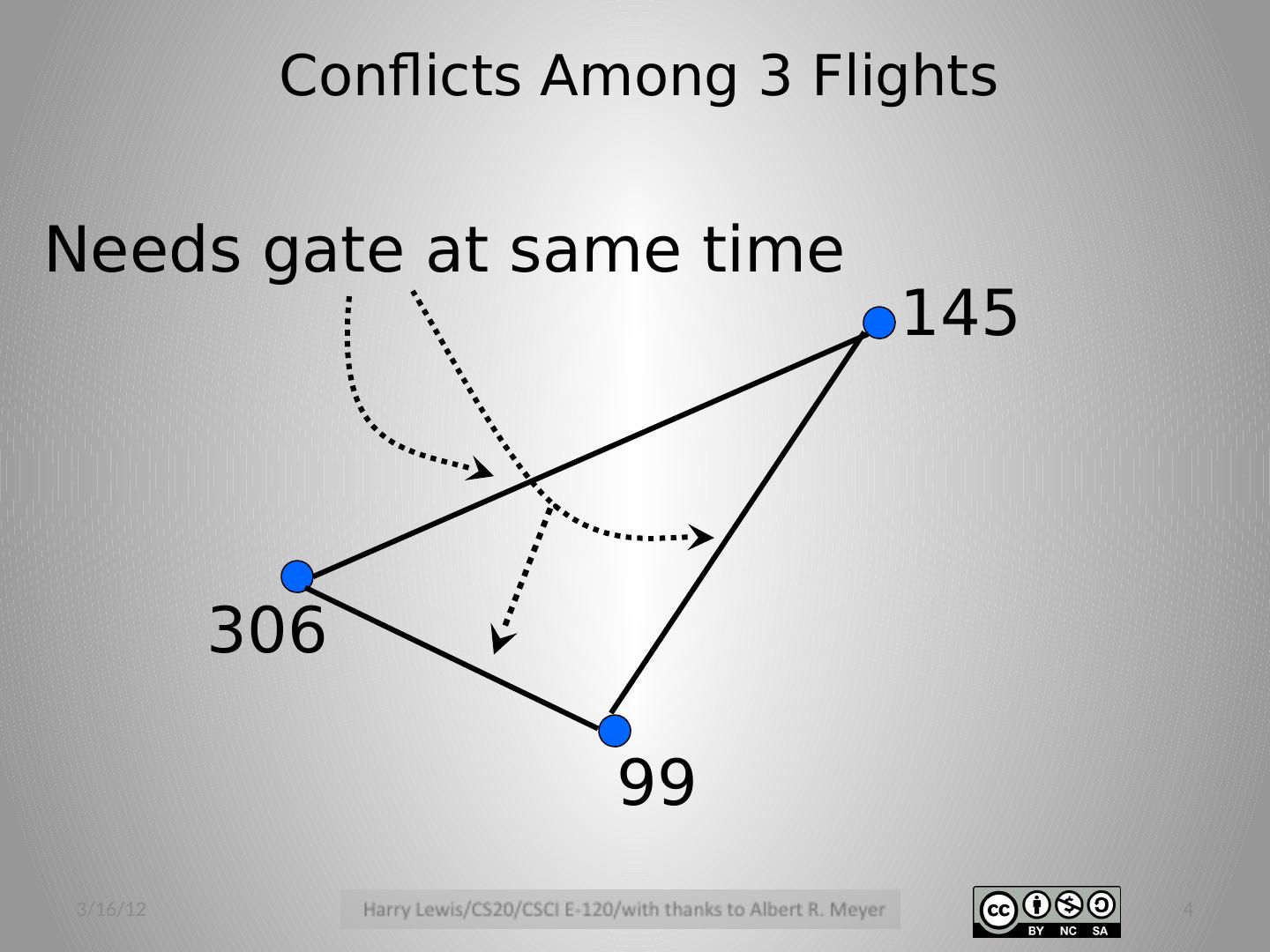
4 .Conflicts Among 3 Flights 99 145 306 Needs gate at same time 3/16/12 4
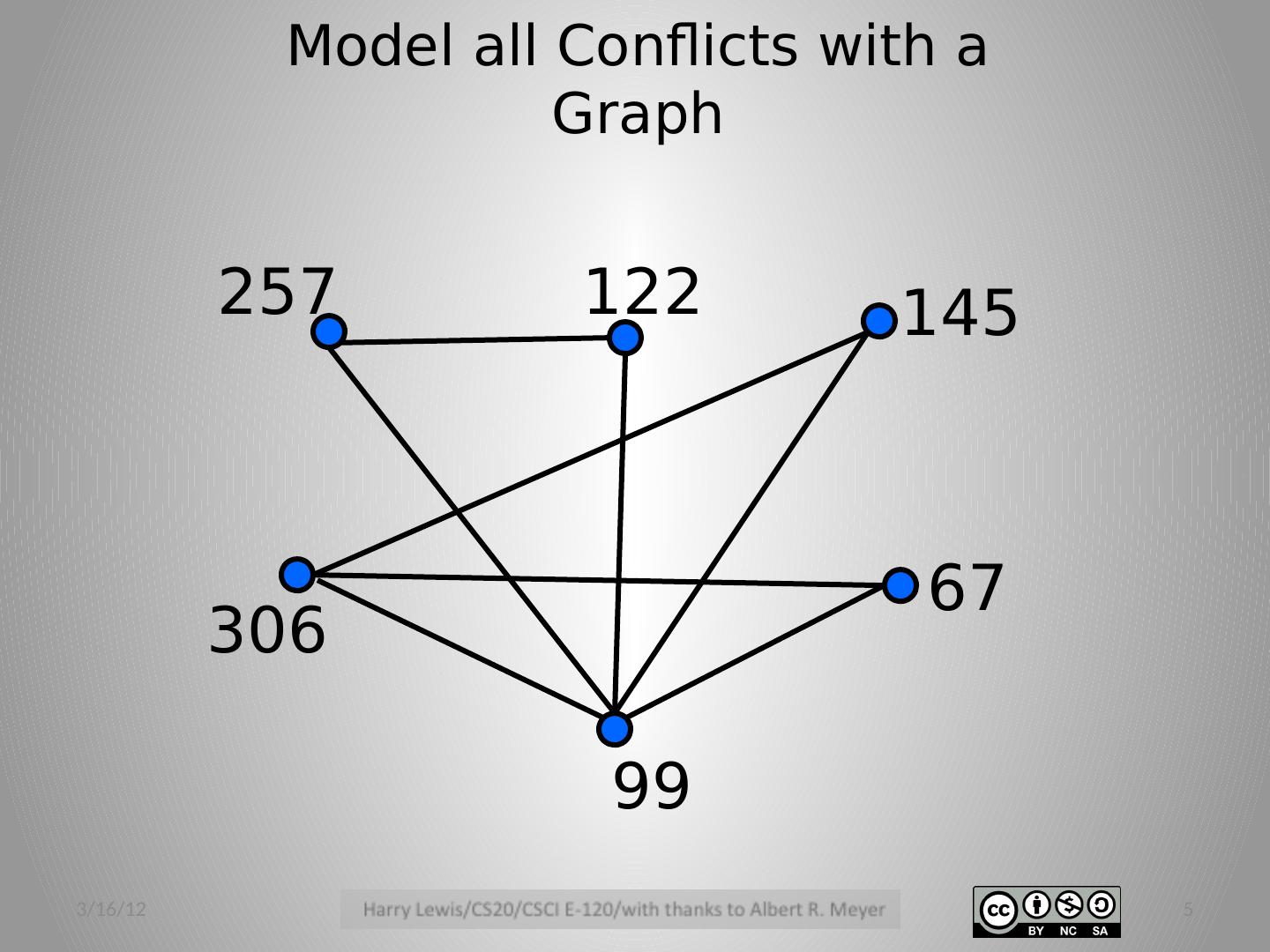
5 .Model all Conflicts with a Graph 257 67 99 145 306 122 3/16/12 5
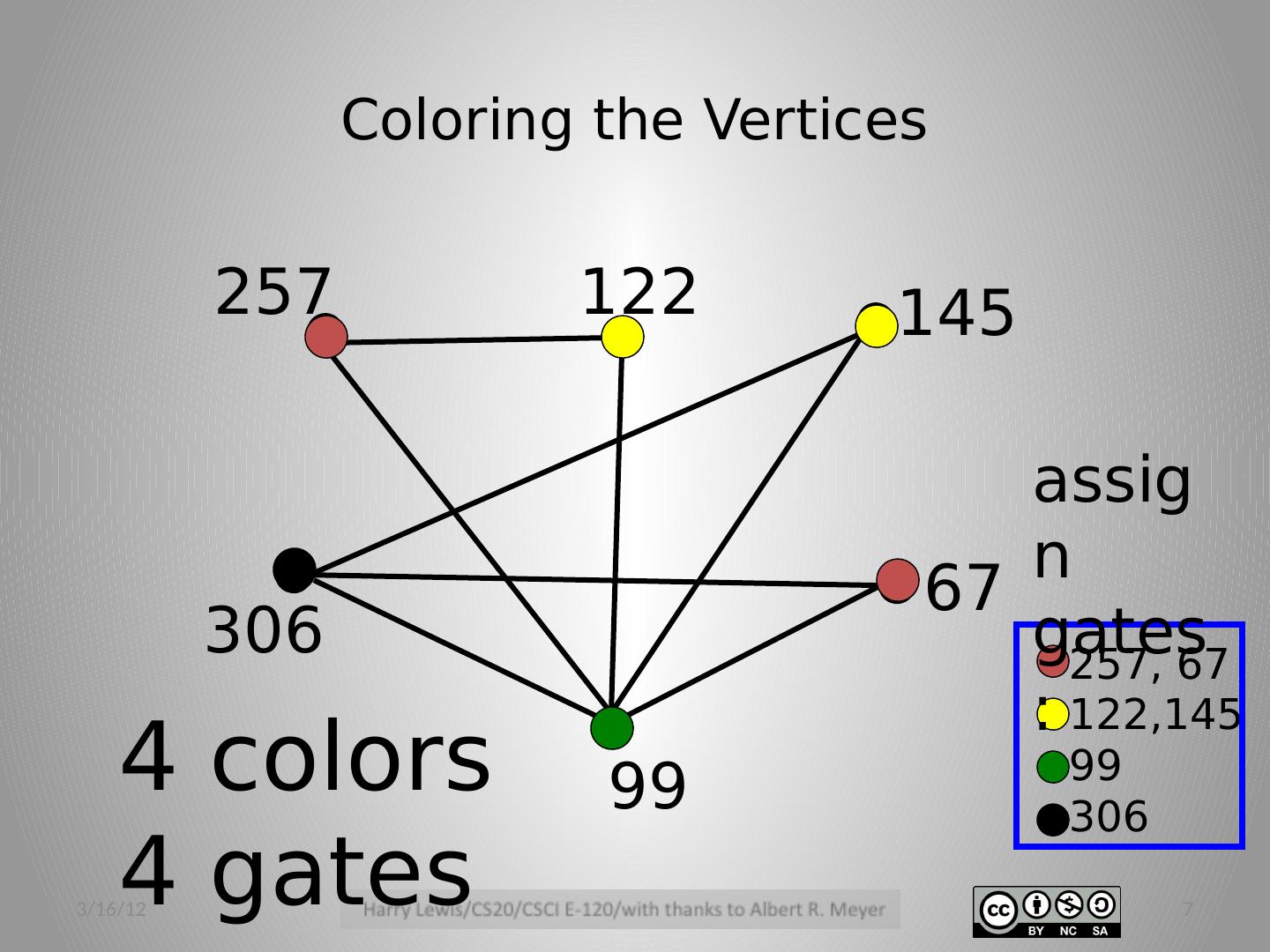
6 .Color vertices so that adjacent vertices have different colors. min # distinct colors needed = min # gates needed Color the vertices 3/16/12 6
7 .Coloring the Vertices 257, 67 122,145 99 306 4 colors 4 gates assign gates: 257 67 99 145 306 122 3/16/12 7
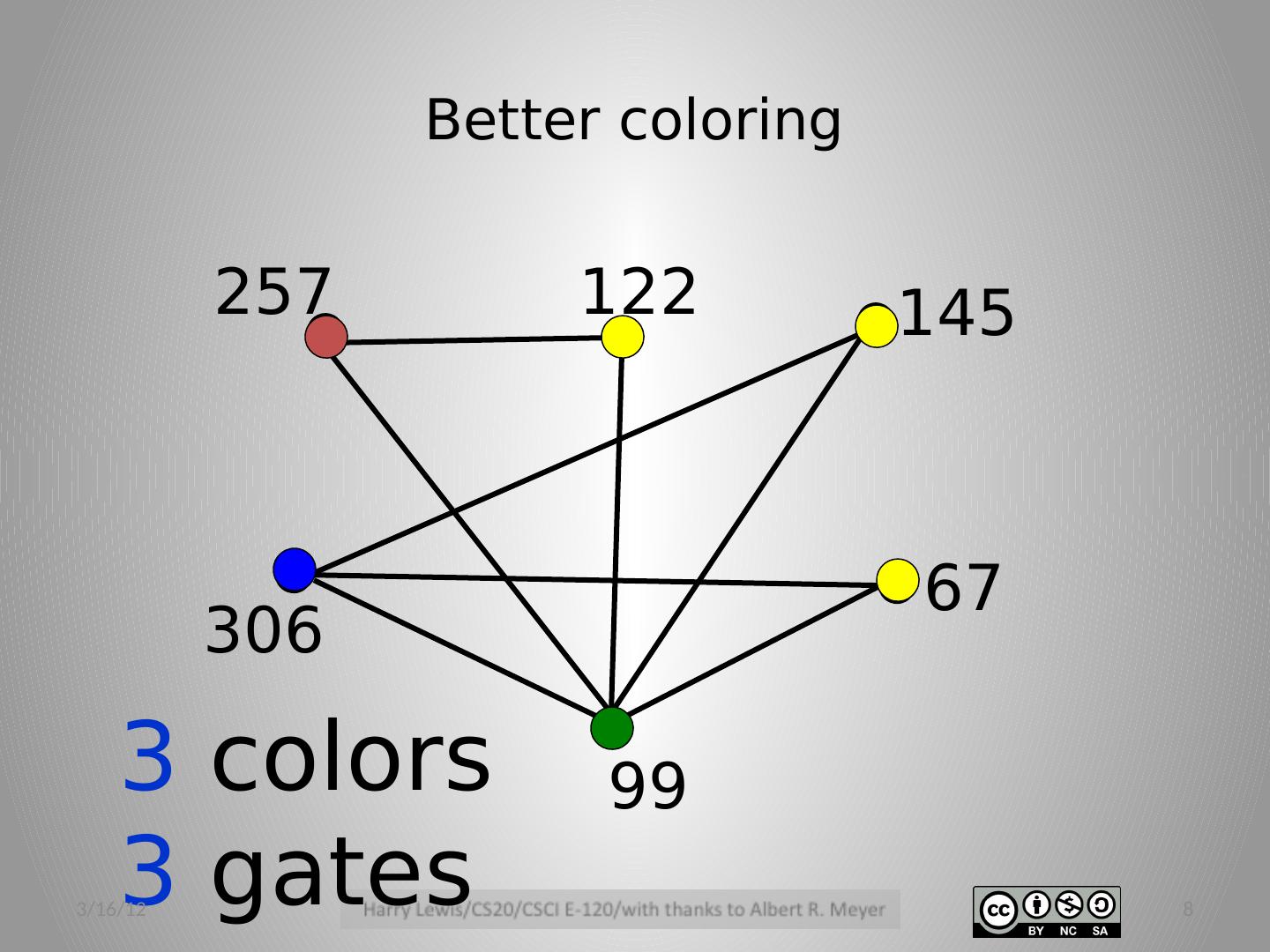
8 .Better coloring 3 colors 3 gates 257 67 99 145 306 122 3/16/12 8
9 .Final Exams Courses conflict if student takes both, so need different time slots. How short an exam period? 3/16/12 9
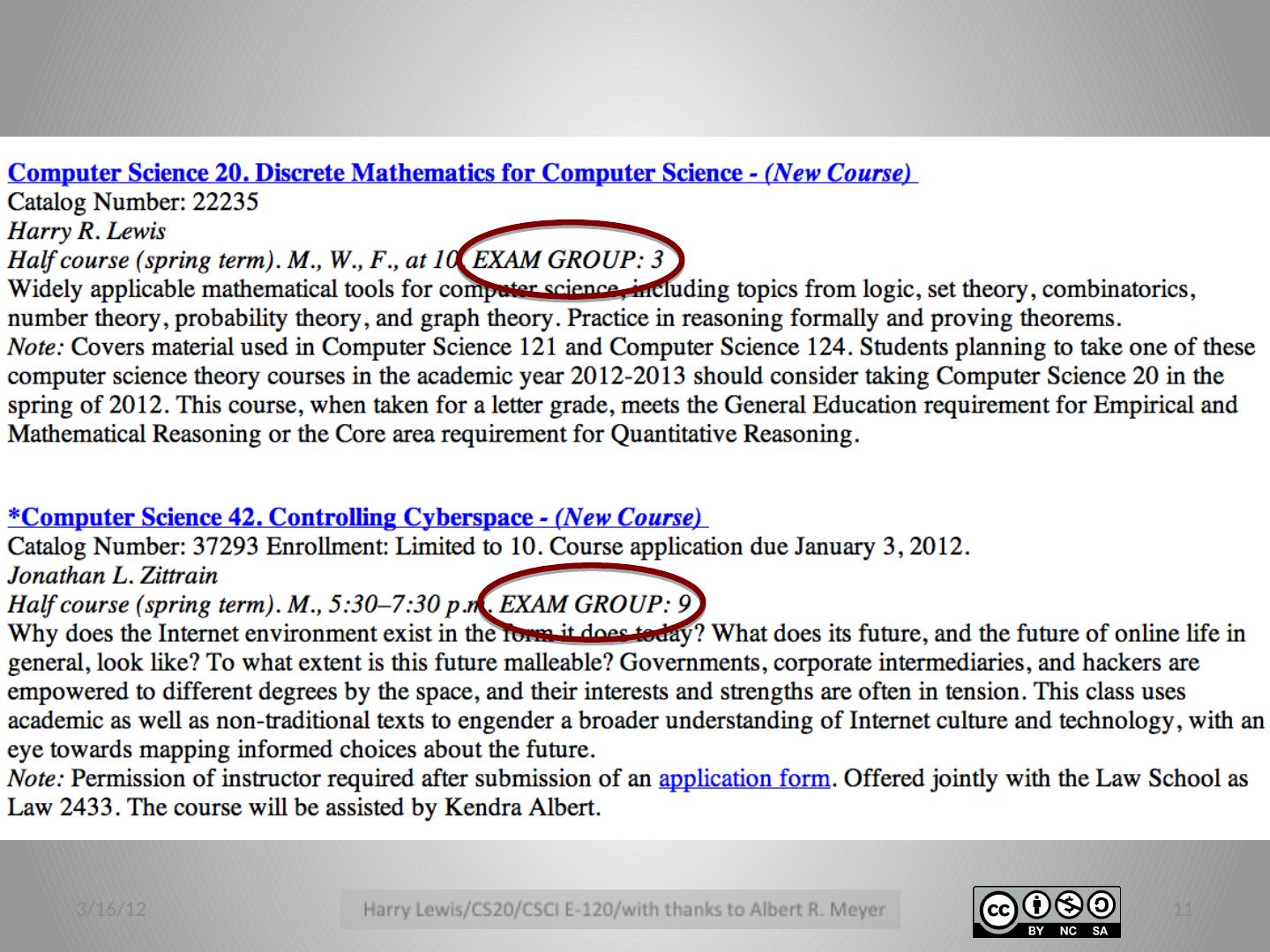
10 .Harvard’s Solution Different “exam group” for every teaching hour. Exams for different groups at different times. 3/16/12 10
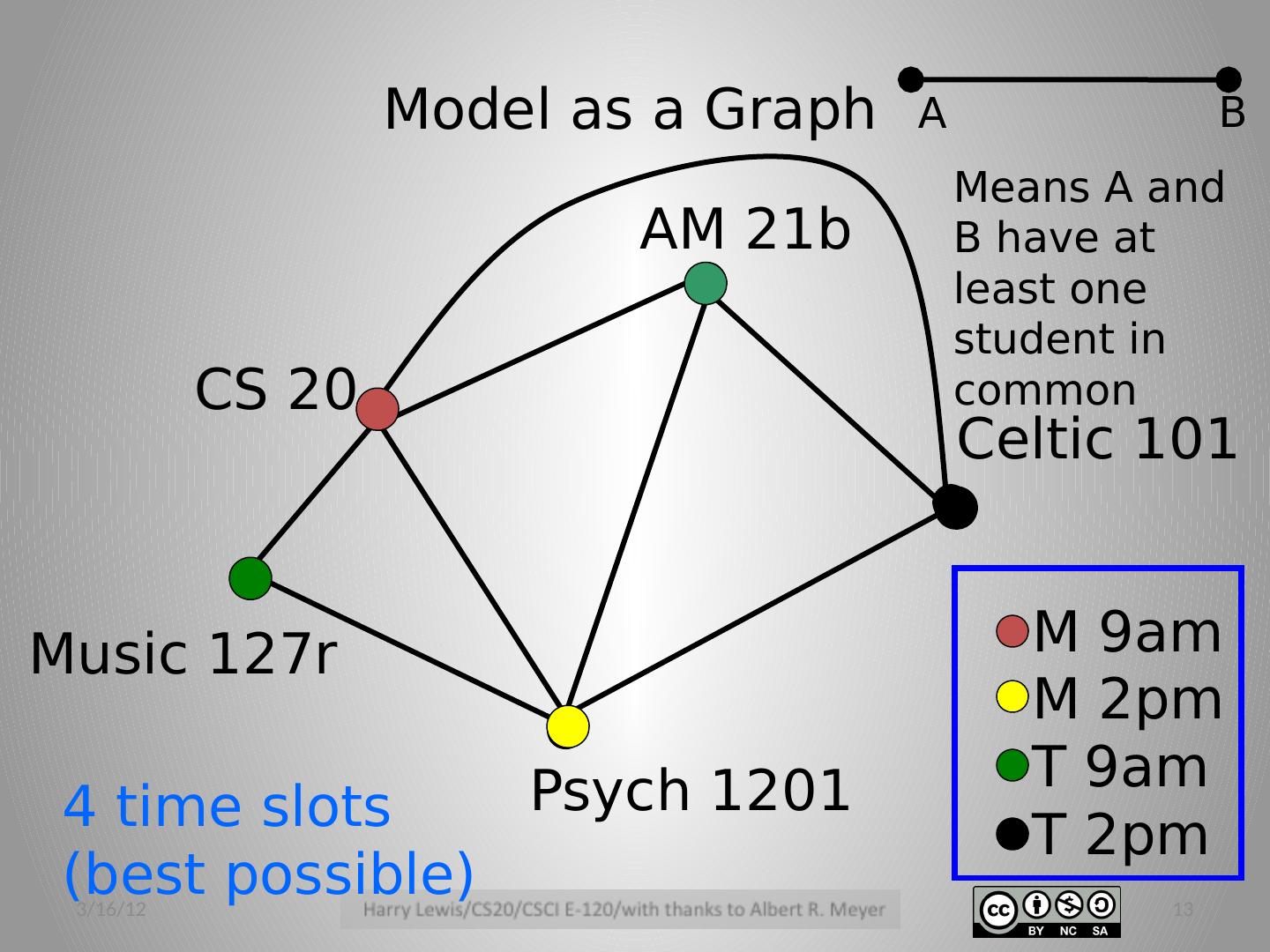
12 .But This May be Suboptimal Suppose course A and course B meet at different times If no student in course A is also in course B, then their exams could be simultaneous Maybe exam period can be compressed! (Assuming no simultaneous enrollment) 3/16/12 12
13 .Model as a Graph CS 20 Psych 1201 Celtic 101 Music 127r AM 21b M 9am M 2pm T 9am T 2pm 4 time slots (best possible) A B Means A and B have at least one student in common 3/16/12 13
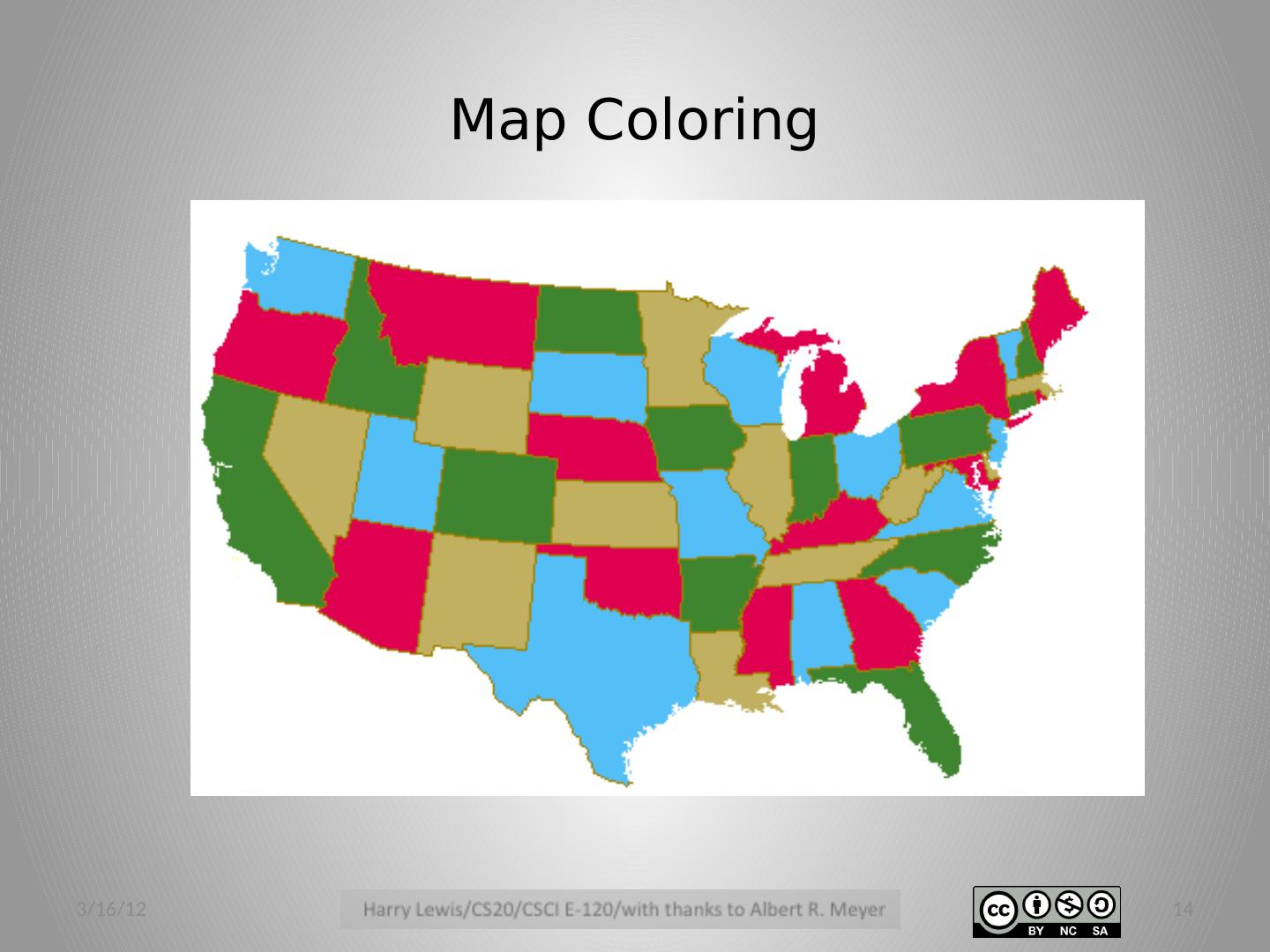
14 .Map Coloring 3/16/12 14
15 .Planar Four Coloring any planar map is 4-colorable. 1850’s: false proof published ( was correct for 5 colors). 1970’s: proof with computer 1990’s: much improved 3/16/12 15
16 .Chromatic Number min #colors for G is chromatic number, χ ( G ) lemma: χ ( tree ) = 2 3/16/12 16
17 .Pick any vertex as “root.” if (unique) path from root is even length: odd length: Trees are 2-colorable root 3/16/12 17
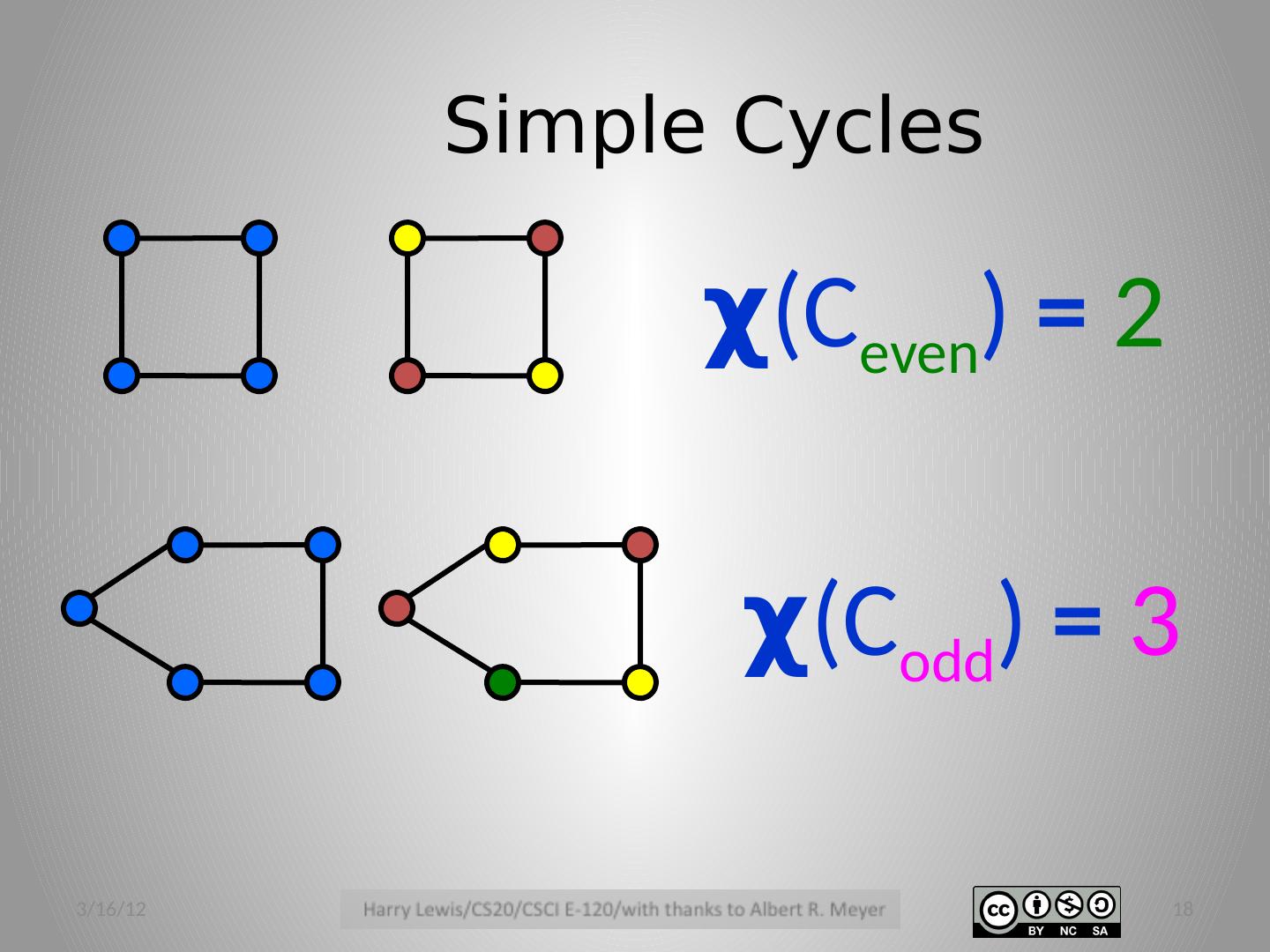
18 .Simple Cycles χ (C even ) = 2 χ (C odd ) = 3 3/16/12 18
19 .Bounded Degree all degrees ≤ k , implies very simple algorithm… χ ( G ) ≤ k+1 3/16/12 19
20 .“Greedy” Coloring …color vertices in any order. next vertex gets a color different from its neighbors. ≤ k neighbors, so k +1 colors always work 3/16/12 20
21 .coloring arbitrary graphs 2-colorable? -- easy to check 3-colorable? -- hard to check (even if planar) find χ ( G )? --theoretically no harder than 3-color, but harder in practice 3/16/12 21
