古典概型和几何概率

1 . 1.2: 古典概型和几何概率 张伟平 课件 http://staff.ustc.edu.cn/~zwp/ 论坛 http://fisher.stat.ustc.edu.cn 

2 .第一章事件与概率 1.3 古典概型 . . . . . . . . . . . . . . . . . . . . 2 1.4 几何概型 . . . . . . . . . . . . . . . . . . . . 15 Previous Next First Last Back Forward 1 

3 .1.3 古典概型 称一个随机试验为古典概型, 如果 第一, (有限性) 试验结果只有有限个 (记为 n) , 第二, (等可能性) 每个基本事件发生的可能性相同. 为计算事件 A 的概率, 设 A 中包含 m 个基本事件, 则定义事件 A 的概率为 ( ) m |A| #A P (A) = = 或 n |Ω| #Ω 记号: 为方便起见，以 |A| 或 #A 记事件 A 中基本事件的个数. 计算古典概率, 主要用到排列组合的知识. Previous Next First Last Back Forward 2 

4 . 计数原理 乘法原理 假定进行过程 I 有 n1 中方式，而对于过程 I 的每一个 方式，进行过程 II 都有 n2 种方式。那么，依次进行过程 I 与 II 共 有 n1 n2 种方式。 加法原理 假定进行过程 I 有 n1 中方式，进行过程 II 有 n2 种 方式。那么，进行过程 I 或 II 共有 n1 + n2 种方式。 排列组合 • 从 n 个不同的元素中, 有放回地取出 r 个元素组成的可重复排 列的种数为 nr 种。从 n 个不同的元素中，不放回地取出 r 个 元素组成的不重复排列的种数为 n(n − 1) · · · (n − r + 1) = Pnr . • 从 n 个不同的元素中, 不放回地取 r 个组成的组合，种数为 ( ) n n(n − 1) · · · (n − r + 1) n! = = = Cnr r r! r!(n − r)! Previous Next First Last Back Forward 3 

5 . • 从 n 个不同的元素中, 有放回地取 r 个组成的组合 (不考虑顺 序)，种数为 ( ) n+r−1 r 在运用排列组合公式时, 要清楚次序问题. ↑Example 甲乙丙丁四人进行乒乓球双打练习, 两人一对地结为对打的双方, 有多少种不同的结对方式? ↓Example 可能有人会认为这个问题是简单的组合问题: 从四人中选出两人结为 一对, 剩下的两人结为一对即可. 于是他们算得: 有 C42 = 6 种方式. 但事实是否如此呢? 注意此时并不要求两队之间的顺序, 所以一 共只有 3 种结对方式: C42 /2 = 3 “组合” 是一种 “有编号的分组模式”, 或者说, 按照组合模式计算 出的分组方式数目中, 已经天然地把组的不同编号方式数目计算在内 了. Previous Next First Last Back Forward 4 

6 . ↑Example 欲将 6 个人分为 3 组, 每组 2 人, 分别从事 3 项不同工作, 求分 配方式数. ↓Example 解：先取出两人从事第 1 项工作, 有 C62 种方式; 再取出两人从事第 2 项工作, 有 C42 种方式; 剩下的两人从事第 3 项工作. 所以一共有: 6! 4! 6! C62 · C42 = = = 90 4! · 2! 2! · 2! 2! · 2! · 2! 种分配方式. Previous Next First Last Back Forward 5 

7 . ↑Example 要把 7 人分为 3 个小组, 执行同一种任务, 其中一个组 3 人, 另 两个组各 2 人, 求分组方式数. ↓Example 解: 显然这也是一个 “无编号分组” 问题. 但是却与上面的情况有所 不同. 因为其中有一个 3 人组, 无论是否编号, 它都与其余两个组有 所区别 (编号无非是为了对分出的组加以区分), 所以在按 “有编号分 组模式” 算出分组方式数之后, 只应再除以 2! (即除去两个不加区分 的组的排列顺序数), 故得: 共有 7! 1 7! · = 3! · 2! · 2! 2! 3! · (2!)3 种分组方式. 为了适应这种分为多个 “不同的” 组的问题需求, 人们总结出如 下的 “多组组合模式”: Previous Next First Last Back Forward 6 

8 .多组组合模式： 有 n 个不同元素, 要把它们分为 k 个不同的组, 使得各组依次有 n1 , n2 , · · · , nk 个元素, 其中 n1 +n2 +· · ·+nk = n, 则一共有 n! n1 ! · n2 ! · ... · nk ! 种不同分法. 不尽相异元素的排列模式 有 n 个元素, 属于 k 个不同的类, 同类 元素之间不可辨认, 各类元素分别有 n1 , n2 , · · · , nk 个, 其中 n1 + n2 + · · · + nk = n, 要把它们排成一列, 则一共有 n! n1 ! · n2 ! · · · nk ! 种不同排法. Previous Next First Last Back Forward 7 

9 . ↑Example 一批产品有 N 个，其中废品有 M 个。现从中随机取出 n 个， 在以下两种情形下，分别求“其中恰好有 m 个废品”这一事件的概 率。(1) 有放回地选取； (2) 不放回地选取 ↓Example 解:记 A = {其中恰好有 m 个废品}，则 (n) m (1) 有放回情形 |Ω| = N n , |A| = m M (N − M )n−m , 所以 ( ) ( ) n M m (N − M )n−m n ( M )m ( N − M )n−m P (A) = = m Nn m N N (N ) (M )(N −M ) (2) 不放回情形 |Ω| = n , |A| = m n−m , 所以 (M )(N −M ) P (A) = m (Nn−m ) n Previous Next First Last Back Forward 8 

10 . ↑Example n 个 男 生, m 个 女 生 排 成 一 排 (m ≤ n + 1). 求 事 件 A = {任意两个女孩不相邻} 的概率。又若排成一圈，又如何? ↓Example 解:(1) 排成一排 |Ω| = (n + m)!, |A| = n!Cn+1 m m! |A| m n!Cn+1 m! P (A) = = |Ω| (n + m)! (2) 排成一圈 |Ω| = (n + m − 1)!, |A| = (n − 1)!Cnm m! |A| (n − 1)!Cnm m! P (A) = = |Ω| (n + m − 1)! Previous Next First Last Back Forward 9 

11 . ↑Example r 个不同的球任意放入编号为 1 至 n 的 n 个盒子，每球入各盒 均等可能，求下列事件的概率 (1) A={指定的 r 个盒子各含一个球} (2) B={每盒至多有一球} (3) C={某指定盒中恰有 m 个球} ↓Example 解:|Ω| = nr (1) |A| = r! (2) |B| = Cnr r! (3) |C| = Crm (n − 1)r−m 又若球是相同的，则在这里, 由于 r 个球是相同的,n 个盒子是互 不相同的. 因此我们只需要关心各个盒子中的球数, 而无需考虑哪个 球落在哪个盒子中. 我们可把问题设想为： r 个相同的小球已经一字排开, 只须在它们之间加上 n − 1 块隔 板, 把它们隔为 n 段, 然后让各段对号放入相应的盒子即可. 由于盒 子可空, 相当于要将 r + n − 1 个不尽相异的元素进行排列, 其中 1 类 Previous Next First Last Back Forward 10 

12 .元素 (小球) 有 r 个, 另 1 类元素 (隔板) 有 n − 1 个, 所以由不尽相 异元素的排列模式知, 一共有 ( ) ( ) r+n−1 r+n−1 = r n−1 不同分法. 因此 ( ) n+r−1 |Ω| = n−1 (1) |A| = 1 ( ) (2) |B| = nr (r−m+n−1−1) (3) |C| = r−m ( ) ( ) n / n+r−1 P (B) = r n−1 Previous Next First Last Back Forward 11 

13 .注： • 球相异和球相同两种情形下的样本空间是不同的，即机会均等 原则是不同的。(各是什么呢？) • 这个例子是古典概型中一个很典型的问题，不少实际问题可以 归结为它 • 若把球解释为粒子，把盒子解释为相空间中的小区域，则这个 问题便相应于统计物理学里的 Maxwell—Boltzmann 统计 • 生日问题 求 r 个人中没有两个人生日相同的概率．若把 r 个人看作上面 问题中的 r 个不可辨球，而把一年的 365 看作为盒子，则 n = 365， 这时记 B 为所求概率事件。则 例如当 r = 40 时，P (B) = 0.109，这个概率已经相当小；而当 r = 50 时, P (B) = 0.03, r = 55 时，P (B) = 0.01, 这实在是出乎意 料地小。 Previous Next First Last Back Forward 12 

14 . ↑Example 设有方程 x + y + z = 15, 试分别求出它的正整数解和非负整数 解 (x, y, z) 的组数. ↓Example 解：本题可以设想为将 15 个无区别的小球分入 3 个不同的盒子, 再 分别将第 1, 2, 3 个盒中的球数对应为 x, y, z 的值即可. 所以, 非负整 数解的组数 (相当于允许出现空盒的情况) 为： 15 2 17 × 16 C15+3−1 = C17 = = 136; 2 而正整数解的组数 (相当于不允许出现空盒的情况) 为： 3−1 2 14 · 13 C15−1 = C14 = = 91. # 2 注: 此例的方法即是证明前面排列组合的方法。 Previous Next First Last Back Forward 13 

15 . ↑Example 设有 n 个人随机地坐到礼堂第一排 N 个座位上去，试求下列事 件的概率：(1) 任何人都没有邻座；(2) 每人恰有一个邻座；(3) 关于 中央座位对称的两个座位至少有一个空着。 ↓Example 解:分别用 A, B, C 表示上述 (1)-(3) 各事件。则 |Ω| = n PN . (1) 视此 n 个人为“女生”，N − n 个座位为“男生”，则 |A| = n CN −n+1 n! n/2 (2) |B| = CN −n+1 n! (3) { n n CN /2 2 n!, N is even |C| = n−1 nC(N −1)/2 2n−1 (n − 1)! + n C(N n −1)/2 2 n!, N is odd Previous Next First Last Back Forward 14 

16 .1.4 几何概型 在实际中，我们还会碰到样本点无限多的情形。几何概型是其中 的一种. 设 Ω 是欧氏空间中确定的集合，满足条件 0 < m(Ω) < +∞。 对 Ω 中的任何可测子集 A, 称 m(A) P (A) = Definition m(Ω) 为事件 A 的几何概率。这里等可能性体现在“落在区域 A 的概率与区域 A 的测度成正比并且与其形状位置无关。" 这里 m(Ω) 表示 Ω 的 “大小”. Previous Next First Last Back Forward 15 

17 . ↑Example 甲乙两人约定在 [0, T ] 时段内去某地会面，规定先到者等候一段 时间 t(t ≤ T ) 再离去。试求事件 A={甲乙将会面} 的概率。 ↓Example 解: 以 x, y 分别表示甲乙到达会面地点的时间。则 Ω = {(x, y)|0 ≤ x, y ≤ T } 而 A = {(x, y)||x − y| ≤ t}, 因此 m(A) t P (A) = = 1 − (1 − )2 . m(Ω) T Previous Next First Last Back Forward 16 

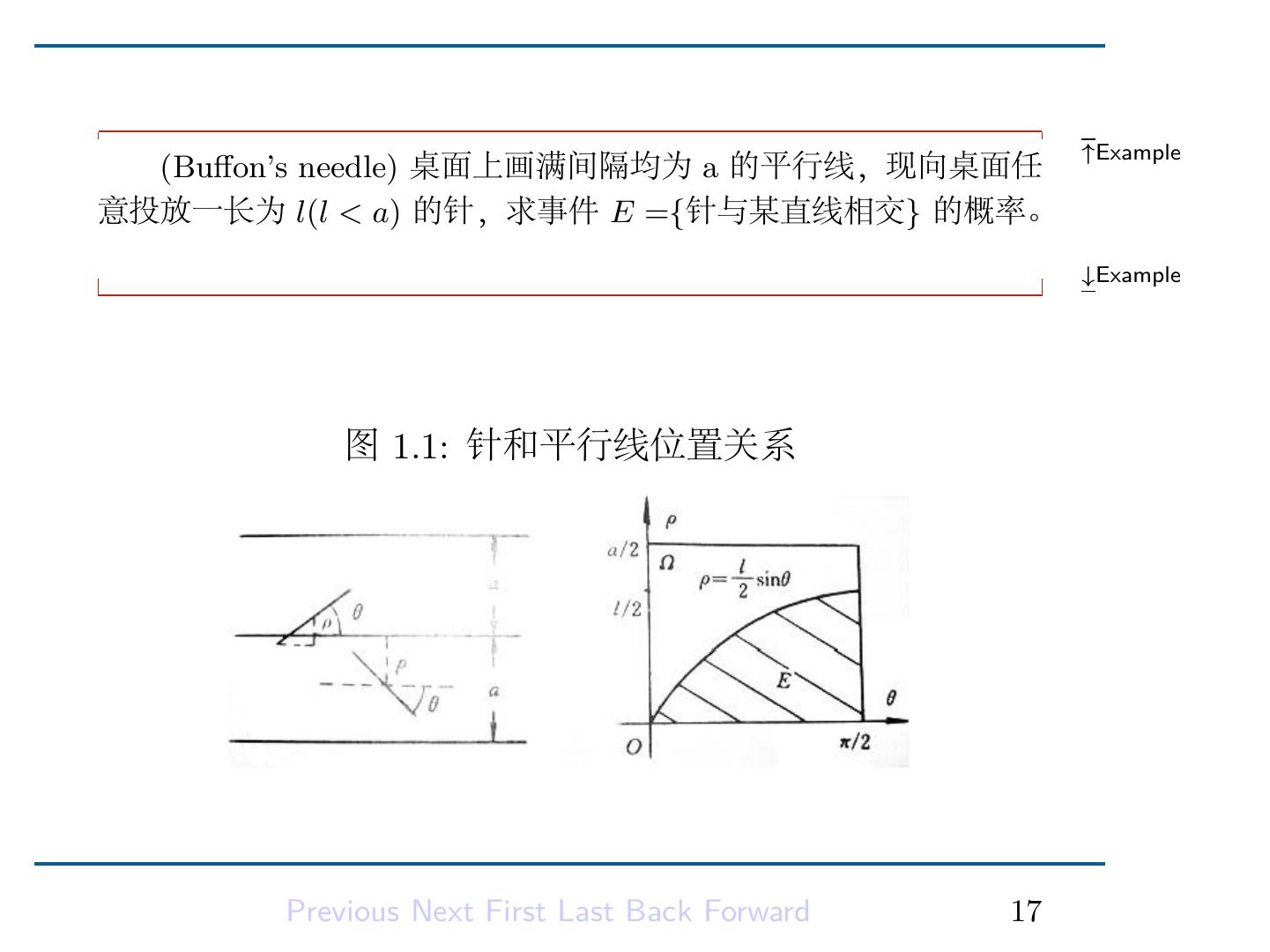
18 . ↑Example (Buffon’s needle) 桌面上画满间隔均为 a 的平行线，现向桌面任 意投放一长为 l(l < a) 的针，求事件 E ={针与某直线相交} 的概率。 ↓Example 解：如下图所示，针的位置由针的中点到最近直线的距离 ρ 及针与 图 1.1: 针和平行线位置关系 Previous Next First Last Back Forward 17 

19 . 直线所夹锐角 θ 决定。于是 Ω = {(ρ, θ) : 0 ≤ ρ ≤ a/2, 0 ≤ θ ≤ π/2}. 由针的任意性，样本点 (ρ, θ) 在 Ω 中均匀分布，是几何概型。 而针与某直线相交，当且仅当 ρ ≤ 2l sinθ. 即 l E = {(ρ, θ) ∈ Ω : ρ ≤ sinθ} 2 ∫ π/2 πa l m(Ω) = , m(E) = sinθdθ 4 0 2 所以 m(E) 2l P (E) = = . m(Ω) πa 从而 2l π≈ pˆa 值得注意的是这里采用的方法：建立一个概率模型，它与某些我 们感兴趣的量 —这里是常数 π—有关，然后设计随机试验，并通过 这个试验的结果来确定这些量。这也就是 Monte-Carlo 思想. Previous Next First Last Back Forward 18 

20 . ↑Example 在圆周上任取三点 A, B, C，求事件 E={△ABC 为锐角三角形} 的概率。(1/4) ↓Example ↑Example 在圆上任取两点 A, B 连成一条弦，再任取两点 C, D 连成一弦， 求 AB 与 CD 相交的概率。(1/3) ↓Example Previous Next First Last Back Forward 19