- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Arithmetic
展开查看详情
1 .Arithmetic
2 .I. Fast Multiplication and the Master Theorem on Divide and Conquer
3 .How fast can we multiply? Adding two n -bit numbers takes O(n ) operations How many operations to multiply two n -bit numbers? Or two n -decimal-digit numbers Difference is a factor of log 2 10 ≈ 3.32 but the individual operations are harder
4 .Grade School Algorithm is Θ(n 2 ) But answer is only O(n ) bits: Can we do better?
5 .A Divide and Conquer Algorithm Suppose n is even, n = 2m To compute a∙b Write a = a 1 ∙2 m + a 0 , b = b 1 ∙2 m + b 0 , where a 1 , a 0 , b 1 , b 0 are m -bit numbers (numbers < 2 m ) – the first and last m bits of a and b a∙b = a 1 b 1 ∙2 2m + (a 1 b 0 +a 0 b 1 )∙2 m + a 0 b 0 = a 1 b 1 ∙(2 2m +2 m ) + (a 1 -a 0 )(b 0 -b 1 )∙2 m + a 0 b 0 ∙(2 m +1) Only 3 m -bit multiplications!!!
6 .How Fast? T(1)=1 T(n ) = 3T(n/2) + cn But how to solve this?
7 .Master Theorem on D+C recurrences T(1) = 1 T(n ) = aT(n/b ) + cn e Let L = log b a Recurrence has the solution: T(n ) = Θ(n e ) if e > L T(n ) = Θ(n e log n ) if e = L T(n ) = Θ(n L ) if e < L Binary search: a=1, b =2, e =0, L=0 [Case 2] Merge sort: a=2, b =2, e =1, L=1 [Case 2] Ordinary mult : a=4, b =2, e =1, L=2 [Case 3] Fast mult : a=3, b =2, e =1, L= lg 3 so Θ( n 1.58… ) [Case 3]
8 .lec 4F. 8 Compute 3 13: 3 13 = 3∙3∙3∙3∙3∙3∙3∙3∙3∙3∙3∙3∙3 (12 multiplications, or Θ(exponent )) 3 13 = 3 6 ∙3 6 ∙3 (2 multiplications) 3 6 = 3 3 ∙3 3 (1 multiplication) 3 3 can be computed with 2 multiplications So 2+1+2 = 5 multiplications in all! II: Fast Exponentiation
9 .lec 4F. 9 compute a b using registers X,Y,Z,R X:= a ; Y:= 1; Z:= b ; REPEAT: if Z=0, then return Y R:= remdr(Z,2); Z:= quotnt(Z,2) if R=1,then Y:= X⋅Y X:= X 2 Fast Exponentiation
10 .February 28, 2007 Harvard Bits 10 Powers by Repeated Squaring Problem: compute a b Method 1: multiply a by itself n-1 times Requires n-1 multiplications Method 2: use successive squaring How many times can you divide n by 2 before it is reduced to 1? Repeated squaring requires between log 2 n and 2∙log 2 n multiplications Huge savings! n = 1000 => at most 20 multiplications! ( since log 2 1000 < 10)
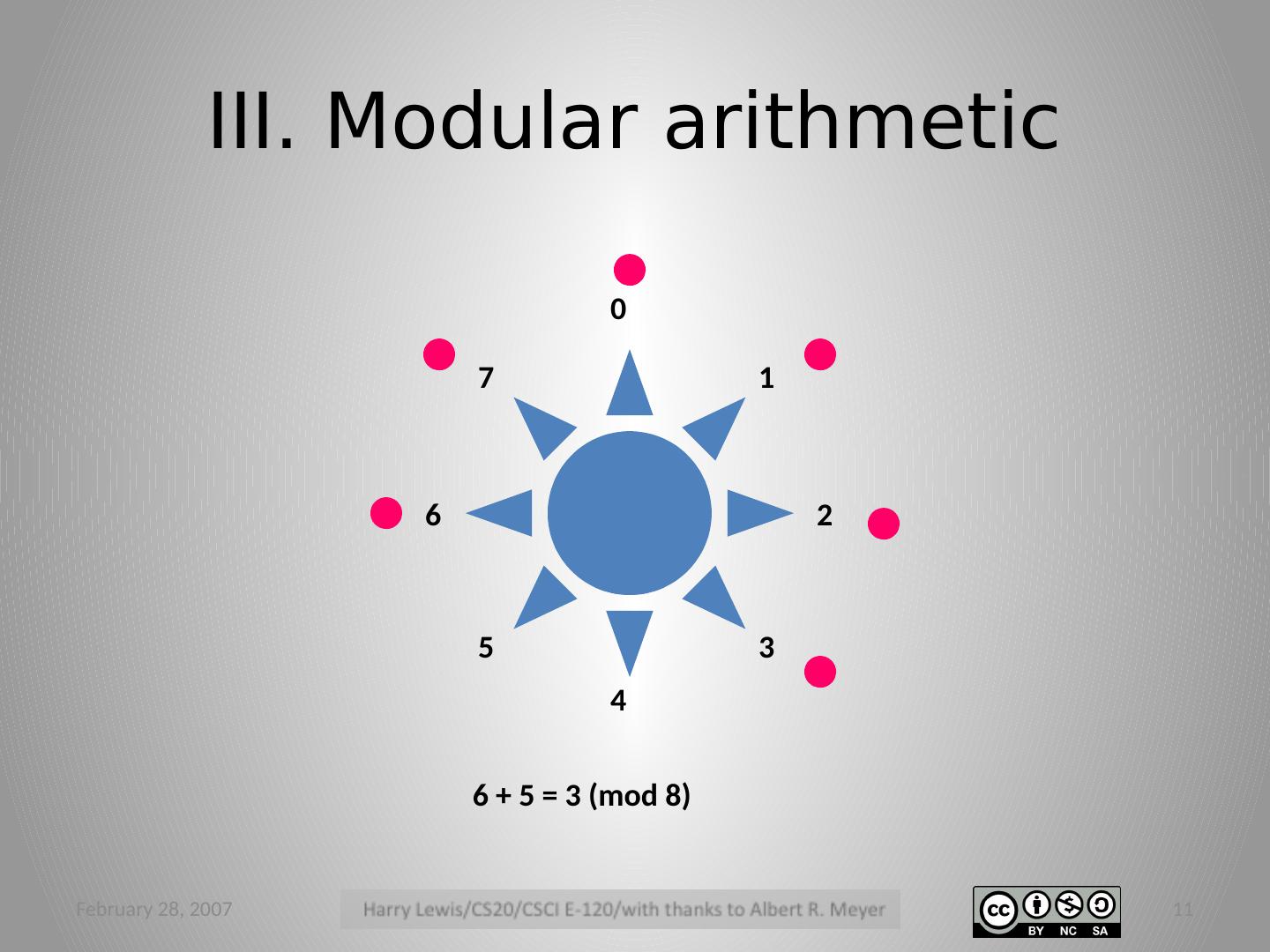
11 .February 28, 2007 11 III. Modular arithmetic 1 2 3 4 5 6 7 0 6 + 5 = 3 (mod 8)
12 .February 28, 2007 12 Math Quiz 2 x 6 = mod 11 2 x 6 x 5 = mod 11 2 3 = mod 7 2 300 = mod 7 1 1 5 1 = (2 3 ) 100 = 1 100 = 1
13 .February 28, 2007 Harvard Bits 13 (mod p ) notation Think of the (mod p ) at the end of the line as referring to everything in the equation (2 3 ) 100 = 1 100 = 1 (mod 7) means “(2 3 ) 100 , 1 100 , and 1 are all equivalent if you divide by 7 and keep just the remainder ” Often written a ≡ b (mod p )
14 .February 28, 2007 Harvard Bits 14 Fast Modular Exponentiation Problem: Given q and p and n , find y < p such that q n = y (mod p ) Method 1: multiply q by itself n-1 times Requires n-1 multiplications Method 2: use successive squaring Requires about log 2 n multiplications Same idea works for multiplication modulo p Example: If n is a 500-digit number, we can compute q n (mod p ) in about 1700 (= lg 10 500 ) steps.
15 .FINIS