模拟电子技术

1 .Course Analog Electronic Technology ( 模拟电子技术 ) Microelectronic Circuits (5th Edition) A . Sedra , K. Smith Textbook Quality Course Shanghai Municipal Education Commission ( 上海市精品课程 )

2 .About teachers CHEN, Jianping ( 陈建平 ) Ph D, Prof., EE Dept. YANG, Hua ( 杨华 ) Ph D, A. Prof., EE Dept. Office: Room 804, Adm. Bldg. B Tel: 34206241 Lab: Room 5-215, SEIEE Bldgs Tel: 34205140 Lab: Room 5-521, SEIEE Bldgs Tel: 34204506 e-mail : jpchen62@sjtu.edu.cn e-mail : hyang@sjtu.edu.cn J. Chen & H.Yang

3 .About the syllabus J. Chen Part I Devices and Basic Circuits ( CHEN ) Chapter 1: Introduction to Electronics Ch apter 2: Operational Amplifiers Chapter 3: Diodes Chapter 4: MOS Field-Effect Transistors (MOSFETs) Chapter 5: Bipolar Junction Transistors (BJTs )

4 .About the syllabus J. Chen Part 2 Digital & Analogue IC ( YANG ) Chapter 6 : Single-Stage Amplifier Chapter 7: Differential and Multistage Amp. Chapter 8: Feedback Chapter 9: Op-Amp & Data-Converter Circuits Chapter 10: CMOS Logic Circuits

5 .About the syllabus J. Chen Part 3 Selected Topics( YANG ) Chapter 11: Memory and Advanced Digital Circuits Chapter 12: Filters and Tuned Amplifiers Chapter 13: Signal Generators and Waveform-Shaping Circuits Chapter 14: Output Stages and Power Amplifiers

6 .About the syllabus J. Chen Appendix VLSI Fabrication Technology Two-Port Network Parameters Some Useful Network Theorems Single-Time-Constant Circuits S-domain Analysis: Poles, Zeros, and Bode Plots

7 .About the syllabus J. Chen Pls refer to: electsys.sjtu.edu.cn ( 教学信息服务网 ) for details

8 .Background: Era of Microelectronics J. Chen 2

9 .In the first half of 20 th Century J. Chen History in brief: vacuum tubes The first computer (1945) The first computer In China (1958) Vacuum Tubes (1906) Below 1 Hz & 30 Ton !

10 .Since the middle of 20th Century J. Chen History in brief: transistors Shockley Bardeen Brattain Invention of Transistor Bell Lab1947 Various diodes and transistor — discrete devices ( 分立器件 )

11 .J. Chen Discrete v.s. integrated Discrete devices very low cost effectiveness limited functionality large volume, weight and power consumption Integrated circuit (IC) semiconductor wafer with thousands of tiny devices fabricated on it powerful function, building-block approach mass production capability, high reliability

12 .J. Chen Integrated circuit The first IC (1958) Invention of IC Refer to App. A for more information about VLSI Fabrication Technology

13 .J. Chen Development of microelectronics The first Apple The first mouse Microelectronics, one of the greatest technology innovations , has been changing the world by penetrating itself into any places where signals are to be obtained, processed and transmitted.

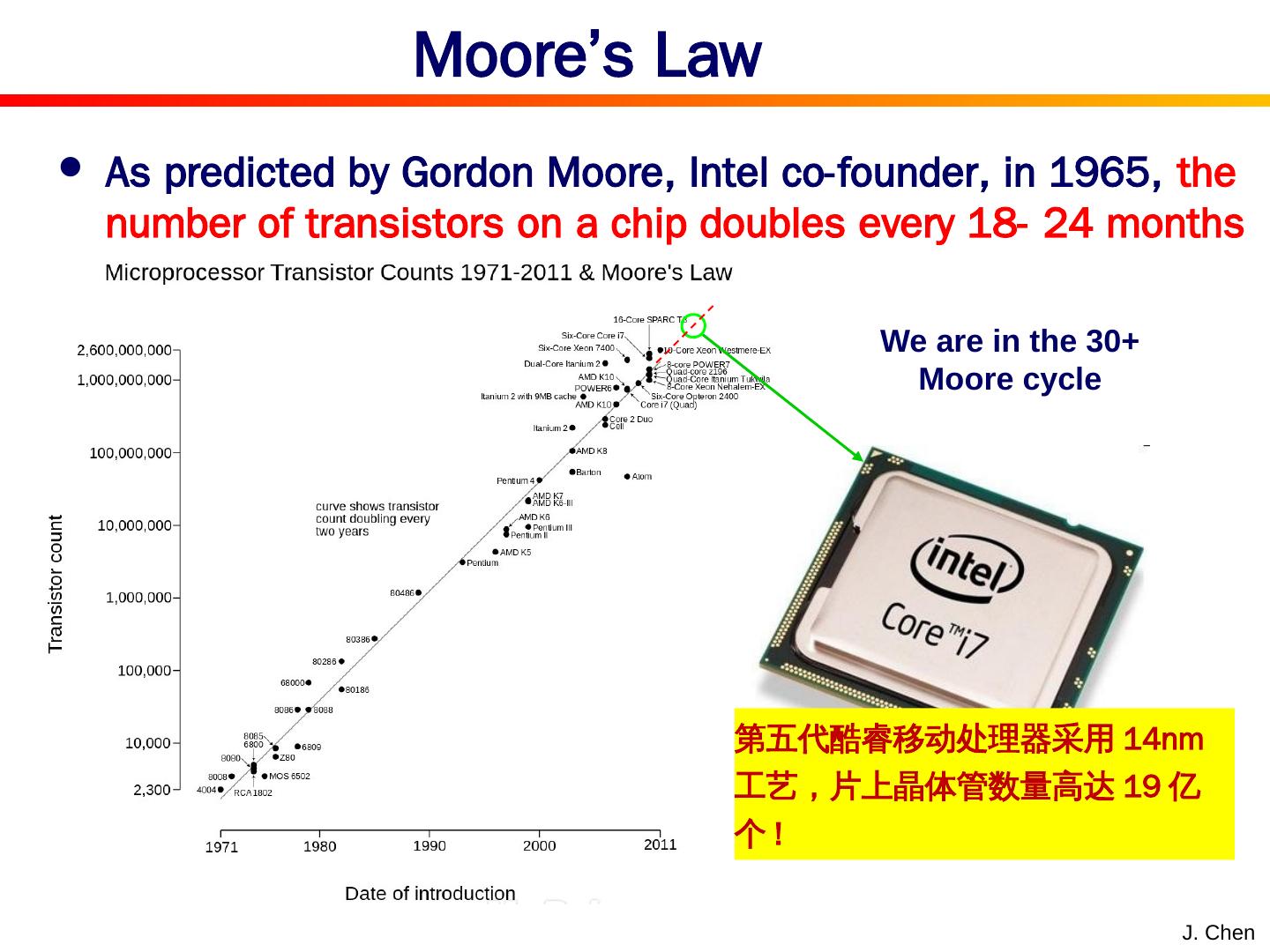
14 .Moore’s Law As predicted by Gordon Moore, Intel co-founder, in 1965, the number of transistors on a chip doubles every 18- 24 months J. Chen We are in the 30+ Moore cycle 第五代酷睿移动处理器采用14nm工艺， 片上 晶体管数量高达19亿个 !

15 .J. Chen Analog and digital An IC is categorized as either analog or digital , depending on its intended application amplifier, oscillator, etc. timer, computer memory, microprocessor, etc. This course pays attention mainly to the analog part

16 .J. Chen The course objective A fundamental course providing essential knowledge for electrical and electronic related areas

17 .J. Chen About the teaching method In class Attention will be paid to the principles and fundamentals e.g. physical operation and electric characteristics of diodes and transistors will be explained in detail by adding some basic knowledge of semiconductors Emphasis will be mainly focused on qualitative analysis and consequently, What is taught may be different from the textbook both in content and order

18 .J. Chen About the teaching method Outside class S elf- study before and after the class is required for better understanding of what you are learning Exercises are another way to strengthen your quantitative analysis ability Additional benefit: intensive reading may also greatly improve both your essential and professional English ability

19 .J. Chen About the notes & exercises Taking notes is a ubiquitous way for effective learning PPT can be found on the net for your reference ( http://eelab.sjtu.edu.cn/analog/ ) . You may also copy them or ask me to send them to you via e-mail. Exercises are mandatory . They are useful to help you in solidifying your knowledge Once a week on every Monday

20 .J. Chen About Q&A No settled schedule for Q&A. It may be arranged for the final examination if needed. You are welcome for any questions before and after the class. You can also contact us via e-mail and telephone. CHEN, Jianping Tel: 34206241 e-mail : jpchen62@sjtu.edu.cn YANG, Hua Tel: 34204506 e-mail : hyang@sjtu.edu.cn

21 .Adapt yourselves for the new course J. Chen Basics of Electricity Ideal Components Intuitional ( 直观的 ) mathematic description Idealized values and units for analysis convenience: V, A, , H… Linear devices … This course Practical components Complex mathematic model (expressions) Exact range of values : V/mV, mA/ A, k/M, mH/H, F/nF/pF… Nonlinear devices …

22 .J. Chen Manage yourselves “Thin” the book by intensive learning Grasp essential knowledge and fundamental ability the concepts, the basic circuits and the analysis methods the ability to further study the new knowledge and apply it to solve practical problems. Enable yourselves with the capacity to Read (qualitative analysis) Calculate (quantitative analysis) Select/design (devices, parameters, circuits, etc.)

23 .J. Chen About the terminology The Chinese translations of the words in black should be kept in mind not only for this course, but also for future use .

24 .J. Chen About components/parts The exact value of a device (both active and passive ) is always deviated from its marked figure, i.e. Standard E Values (a few discrete numbers) There are different grades of Standard tolerance

25 .J. Chen Standard E value and tolerance

26 .J. Chen Color code

27 .J. Chen About simplification Simplification is always needed in this area for analysis and design convenience Variable devices, e.g. variable resistor, can be used for adjustment, if needed General rules ： if two or more quantities are different by at least an order , the “smaller” one can be ignored R 1 >> R 2 R 1 R 1 R 2 R 2 R 1 >> R 2 R 1 R 2 C 1 >> C 2 C 1 C 1 C 2 C 2 C 1 C 2 C 1 >> C 2

28 .J. Chen About simplification Ignorable is the relatively smaller quantity for analysis convenience. The device with absolute small value can not be dropped in practical circuit design Drive Circuit of Laser Diode electrolytic capacitor ceramic capacitor

29 .J. Chen Choice of a device Refer to manual for details Power dissipation is an important factor to be considered. Components (except for inductive components ) consume electrical power and convert it into heat, resulting in temperature rising The load capacity of a resistor is determined by its power rating ( 额定功率 ) , which usually lies in the range of 0.05 一 500 W. In practical design, the rating power of a resistor should be 1.5-2 times larger than the maximum power consumption. So are the rating powers of diodes, transistors, etc.