ALU设计：Multiplication

1 . ECE468 Computer Organization & Architecture ALU Design II ECE4680 ALU-II.1 2002-2-20 Review: A One Bit ALU °This 1-bit ALU will perform AND, OR, and ADD CarryIn A Mux Result 1-bit Full B Adder CarryOut ECE4680 ALU-II.2 2002-2-20 

2 . Review: Functional Specification of the ALU ALUop 3 A N Zero ALU Result N Overflow B N CarryOut °ALU Control Lines (ALUop) Function • 000 And • 001 Or • 010 Add • 110 Subtract • 111 Set-on-less-than ECE4680 ALU-II.3 2002-2-20 Deriving requirements of ALU °Start with instruction set architecture: must be able to do all operations in ISA °Tradeoffs of cost and speed based on frequency of occurrence, hardware budget °MIPS ISA ECE4680 ALU-II.4 2002-2-20 

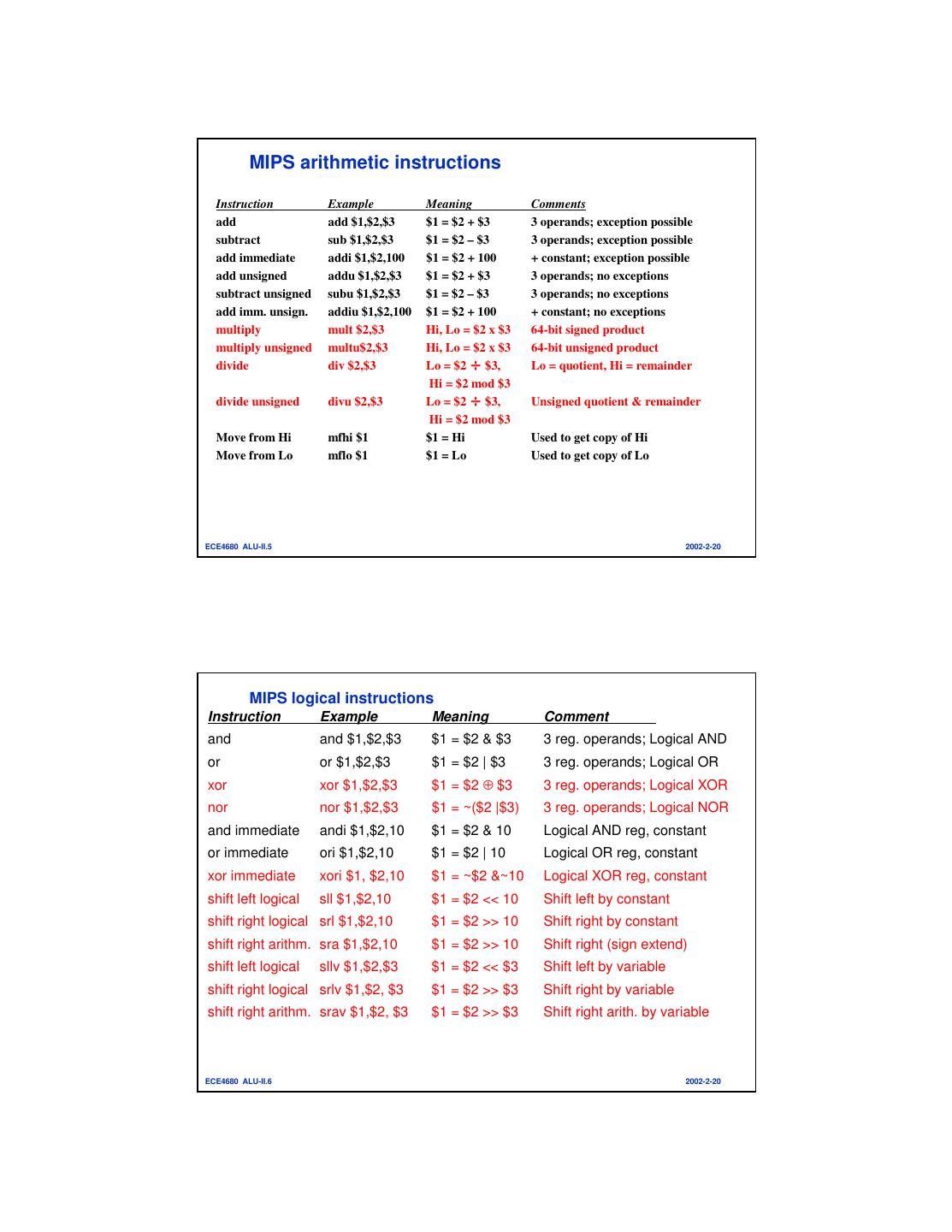
3 . MIPS arithmetic instructions Instruction Example Meaning Comments add add $1,$2,$3 $1 = $2 + $3 3 operands; exception possible subtract sub $1,$2,$3 $1 = $2 – $3 3 operands; exception possible add immediate addi $1,$2,100 $1 = $2 + 100 + constant; exception possible add unsigned addu $1,$2,$3 $1 = $2 + $3 3 operands; no exceptions subtract unsigned subu $1,$2,$3 $1 = $2 – $3 3 operands; no exceptions add imm. unsign. addiu $1,$2,100 $1 = $2 + 100 + constant; no exceptions multiply mult $2,$3 Hi, Lo = $2 x $3 64-bit signed product multiply unsigned multu$2,$3 Hi, Lo = $2 x $3 64-bit unsigned product divide div $2,$3 Lo = $2 ÷ $3, Lo = quotient, Hi = remainder Hi = $2 mod $3 divide unsigned divu $2,$3 Lo = $2 ÷ $3, Unsigned quotient & remainder Hi = $2 mod $3 Move from Hi mfhi $1 $1 = Hi Used to get copy of Hi Move from Lo mflo $1 $1 = Lo Used to get copy of Lo ECE4680 ALU-II.5 2002-2-20 MIPS logical instructions Instruction Example Meaning Comment and and $1,$2,$3 $1 = $2 & $3 3 reg. operands; Logical AND or or $1,$2,$3 $1 = $2 | $3 3 reg. operands; Logical OR xor xor $1,$2,$3 $1 = $2 ⊕ $3 3 reg. operands; Logical XOR nor nor $1,$2,$3 $1 = ~($2 |$3) 3 reg. operands; Logical NOR and immediate andi $1,$2,10 $1 = $2 & 10 Logical AND reg, constant or immediate ori $1,$2,10 $1 = $2 | 10 Logical OR reg, constant xor immediate xori $1, $2,10 $1 = ~$2 &~10 Logical XOR reg, constant shift left logical sll $1,$2,10 $1 = $2 << 10 Shift left by constant shift right logical srl $1,$2,10 $1 = $2 >> 10 Shift right by constant shift right arithm. sra $1,$2,10 $1 = $2 >> 10 Shift right (sign extend) shift left logical sllv $1,$2,$3 $1 = $2 << $3 Shift left by variable shift right logical srlv $1,$2, $3 $1 = $2 >> $3 Shift right by variable shift right arithm. srav $1,$2, $3 $1 = $2 >> $3 Shift right arith. by variable ECE4680 ALU-II.6 2002-2-20 

4 . Compare and Branch °Compare and Branch • BEQ rs, rt, offset if R[rs] == R[rt] then PC-relative branch • BNE rs, rt, offset <> °Compare to zero and branch • BLEZ rs, offset if R[rs] <= 0 then PC-relative branch • BGTZ rs, offset > • BLT < • BGEZ >= • BLTZAL rs, offset if R[rs] < 0 then branch and link (into R 31) • BGEZAL >= ECE4680 ALU-II.7 2002-2-20 MIPS ALU requirements °Add, AddU, Sub, SubU, AddI, AddIU => 2’s complement adder with overflow detection & inverter °SLTI, SLTIU (set less than) => 2’s complement adder with inverter, check sign bit of result °BEQ, BNE (branch on equal or not equal) => 2’s complement adder with inverter, check if result = 0 °And, Or, AndI, OrI => Logical AND, logical OR °ALU from last lecture supports these ops ECE4680 ALU-II.8 2002-2-20 

5 . Additional MIPS ALU requirements °Xor, Nor, XorI => Logical XOR, logical NOR or use 2 steps: (A OR B) XOR 1111....1111 °Sll, Srl, Sra => Need left shift, right shift, right shift arithmetic by 0 to 31 bits °Mult, MultU, Div, DivU => Need 32-bit multiply and divide, signed and unsigned ECE4680 ALU-II.9 2002-2-20 Add XOR to ALU °Expand Multiplexor CarryIn A Mux Result 1-bit Full B Adder CarryOut ECE4680 ALU-II.10 2002-2-20 

6 . Shifters Three different kinds: logical-- value shifted in is always "0" "0" msb lsb "0" arithmetic-- on right shifts, sign extend msb lsb "0" rotating-- shifted out bits are wrapped around (not in MIPS) left right msb lsb msb lsb Note: these are single bit shifts. A given instruction might request 0 to 32 bits to be shifted! ECE4680 ALU-II.11 2002-2-20 Multiplexor/Shifter SHR: SHR 0, 1, 2, 3 bits: Q3 0 D3 Q3 0 Q3 0 0 0 1 0 1 D3 D3 0 1 0 1 Q2 0 D2 0 2 Q2 0 0 Q3 1 0 3 D2 Q3 1 0 1 Q1 0 D1 Q2 0 Q1 0 0 Q2 1 Q3 1 D1 D2 Q2 1 1 Q0 0 0 2 Q0 0 0 D0 D0 Q1 1 0 3 Q1 1 1 SHR/ x2 x1 don't Q0 0 shift Q1 1 8 x 2:1 Mux D0 ( 5 inputs) Q2 2 2 stages Q3 3 shift amount (0,1,2,3) How do arithmetic shift right? 4 x 4:1 Mux 1 stage ( 7 inputs) ECE4680 ALU-II.12 2002-2-20 

7 . General Shift Right Scheme using 16 bit example 15 2 1 0 S0 (0, 1) S1 (0, 2) S2 (0, 4) S3 (0, 8) Shamt = S3S2S1S0 ; If SiS=0, go straight; if Si=0, go skew. If right-to-left connections are added, it could support Rotate Shift Right. ECE4680 ALU-II.13 2002-2-20 MULTIPLY (p250) °Paper and pencil example: Multiplicand 1000 Multiplier x 1001 1000 0000 0000 1000 Product 1001000 °m bits x n bits = m+n bit product °Binary makes it easy: only 2 choices at each step • 1 => place multiplicand ( 1 x multiplicand) • 0 => place 0 ( 0 x multiplicand) °3 versions of multiply hardware & algorithm: successive refinement ECE4680 ALU-II.14 2002-2-20 

8 . Unsigned Combinational Multiplier 0 0 0 0 Initial product A3 A2 A1 A0 B0 A3 A2 A1 A0 B1 A3 A2 A1 A0 B2 A3 A2 A1 A0 B3 P7 P6 P5 P4 P3 P2 P1 P0 °Stage i accumulates A * 2 i if Bi == 1 °Q: How much hardware for 32 bit multiplier? Critical path? ECE4680 ALU-II.15 2002-2-20 How does it work? 0 0 0 0 0 0 0 A3 A2 A1 A0 B0 A3 A2 A1 A0 B1 A3 A2 A1 A0 B2 A3 A2 A1 A0 B3 P7 P6 P5 P4 P3 P2 P1 P0 °at each stage shift A left ( x 2) °use next bit of B to determine whether to add in shifted multiplicand °accumulate 2n bit partial product at each stage ECE4680 ALU-II.16 2002-2-20 

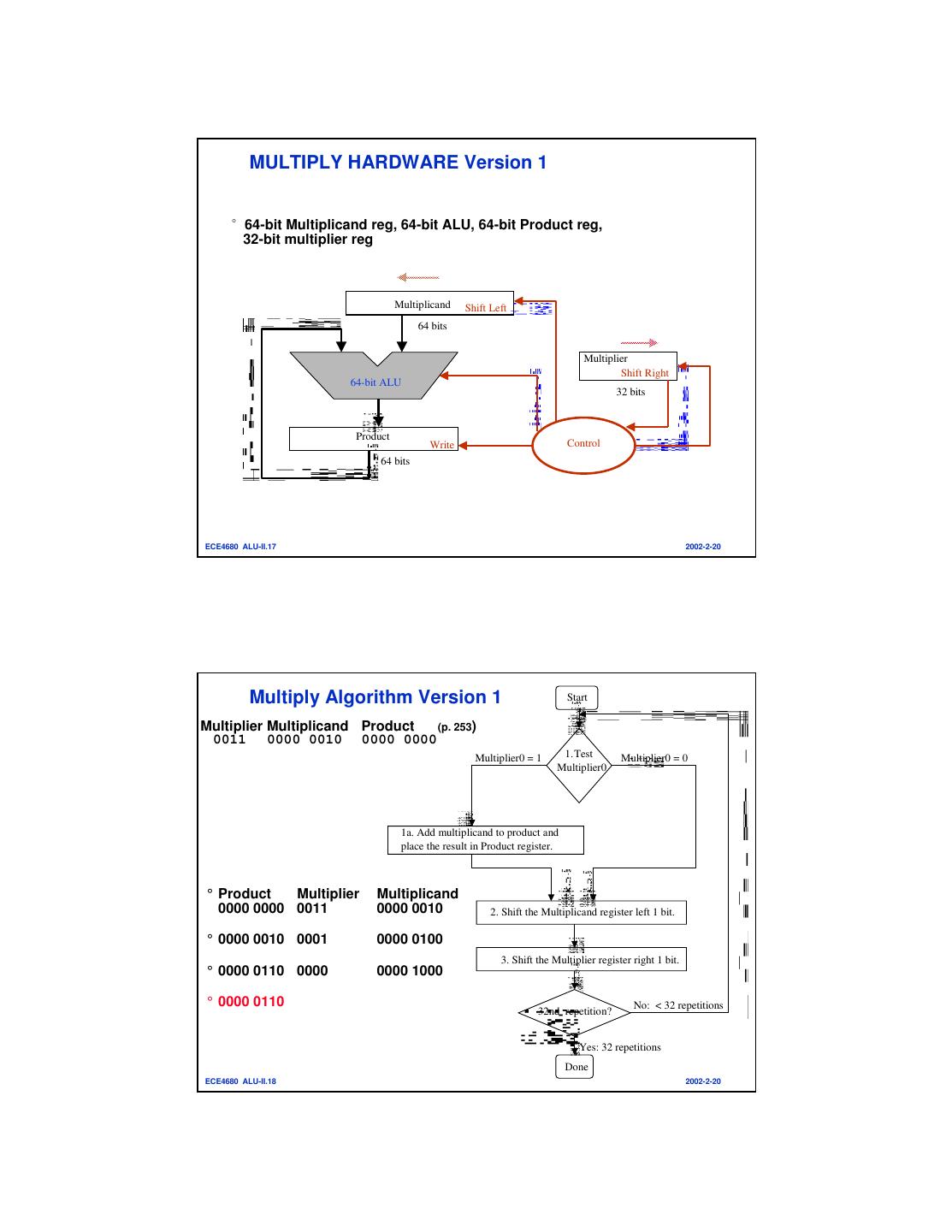
9 . MULTIPLY HARDWARE Version 1 °64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg, 32-bit multiplier reg Multiplicand Shift Left 64 bits Multiplier Shift Right 64-bit ALU 32 bits Product Write Control 64 bits ECE4680 ALU-II.17 2002-2-20 Multiply Algorithm Version 1 Start Multiplier Multiplicand Product (p. 253) 0011 0000 0010 0000 0000 Multiplier0 = 1 1.Test Multiplier0 = 0 Multiplier0 1a. Add multiplicand to product and place the result in Product register. ° Product Multiplier Multiplicand 0000 0000 0011 0000 0010 2. Shift the Multiplicand register left 1 bit. ° 0000 0010 0001 0000 0100 3. Shift the Multiplier register right 1 bit. ° 0000 0110 0000 0000 1000 ° 0000 0110 No: < 32 repetitions 32nd repetition? Yes: 32 repetitions Done ECE4680 ALU-II.18 2002-2-20 

10 . Observations on Multiply Version 1 °1 clock cycle per step => ～ 100 cycles per multiply of two 32-bits. • Ratio of multiply to add 1:5 to 1:100. • Amdahl’s Law: even a moderate frequency of a slow operation can limit performance. °1/2 bits in multiplicand always 0 => 64-bit adder is wasted °0 is inserted in left of multiplicand as shifted => least significant bits of product never changed once formed °Very big, too slow. °Instead of shifting multiplicand to left, shift product to right? ECE4680 ALU-II.19 2002-2-20 What’s going on? 0 0 0 0 Initial product A3 A2 A1 A0 B0 A3 A2 A1 A0 B1 A3 A2 A1 A0 B2 A3 A2 A1 A0 B3 P7 P6 P5 P4 P3 P2 P1 P0 °Multiplicand stays still and product moves right ECE4680 ALU-II.20 2002-2-20 

11 . MULTIPLY HARDWARE Version 2 °32-bit Multiplicand reg, 32 -bit ALU, 64-bit Product reg, 32-bit Multiplier reg Multiplicand 32 bits Multiplier 32-bit ALU Shift Right 32 bits Product Shift Right Write Control 64 bits ECE4680 ALU-II.21 2002-2-20 Multiply Algorithm Version 2 Start Addition performed only on left half of product register Multiplier0 = 1 Multiplier0 = 0 1. Test Multiplier0 Shift of product Register 1a. Add multiplicand to the left half of the product and place the result in the left half of the Product register ° Product Multiplier Multiplicand(p256) ° 0000 0000 0011 0010 2. Shift the Product register right 1 bit ° 0010 0000 0011 0010 ° 0001 0000 0001 0010 3. Shift the Multiplier register right 1 bit. ° 0011 0000 0001 0010 No: < 32 repetitions ° 0001 1000 0000 0010 32nd repetition? ° 0000 1100 0000 0010 Yes: 32 repetitions ° 0000 0110 0000 0010 Done ECE4680 ALU-II.22 2002-2-20 

12 . Observations on Multiply Version 2 °Product register wastes space that exactly matches size of multiplier => combine Multiplier register and Product register ECE4680 ALU-II.23 2002-2-20 MULTIPLY HARDWARE Version 3 °32-bit Multiplicand reg, 32 -bit ALU, 64-bit Product reg, (0-bit Multiplier reg) Multiplicand 32 bits 32-bit ALU Product Shift Right Control Write 64 bits Multiplier ECE4680 ALU-II.24 2002-2-20 

13 . Multiply Algorithm Version 3 Start Multiplicand Product (p257) 0010 0000 0011 Product0=1 Product0=0 1. Test Product0 1a. Add multiplicand to the left half of the product and place the result in the left half of the Product register. ° Product | Multiplier Multiplicand 0000 0011 0010 2. Shift the Product register right 1 bit. ° 0010 0011 0010 ° 0001 0001 0010 No: < 32 repetitions ° 0011 0000 0010 32nd repetition? ° 0001 1000 0010 Yes: 32 repetitions ° 0000 1100 0010 Done ° 0000 0110 0010 ECE4680 ALU-II.25 2002-2-20 Observations on Multiply Version 3 °2 steps per bit because Multiplier & Product combined °MIPS registers Hi and Lo are left and right half of Product °Gives us MIPS instruction MultU °What about signed multiplication? • easiest solution is to make both positive & remember whether to complement product when done (leave out the sign bit, run for 31 steps) • Booth’s Algorithm is more elegant way to multiply signed numbers using same hardware as before ECE4680 ALU-II.26 2002-2-20 

14 . Motivation for Booth’s Algorithm °Example 2 x 6 = 0010 x 0110: 0010 x 0110 + 0000 shift (0 in multiplier) + 0010 add (1 in multiplier) + 0100 add (1 in multiplier) + 0000 shift (0 in multiplier) 00001100 °ALU with add or subtract gets same result in more than one way: 6 = – 2 + 8 , or 0110 = – 0010 + 1000 = 1110 + 1000 °Replace a string of 1s in multiplier with an initial subtract when we first see a one and then later add for the bit after the last one. For example 0010 x 0110 + 0000 shift (0 in multiplier) – 0010 sub (first 1 in multiplier) + 0000 shift (middle of string of 1s) + 0010 add (prior step had last 1) 00001100 ECE4680 ALU-II.27 2002-2-20 Booth’s Algorithm Insight middle of run end of run beginning of run 0 1 1 1 1 0 °Current Bit Bit to the Right Explanation Example 1 0 Beginning of a run of 1s 0001111000 1 1 Middle of a run of 1s 0001111000 0 1 End of a run of 1s 0001111000 0 0 Middle of a run of 0s 0001111000 Originally for Speed since shift faster than add for his machine °Replace a string of 1s in multiplier with an initial subtract when we first see a one and then later add for the bit after the last one –1 + 10000 01111 ECE4680 ALU-II.28 2002-2-20 

15 . Booth’s Algorithm 1. Depending on the current and previous bits, do one of the following: 00: a. Middle of a string of 0s, so no arithmetic operations. 01: b. End of a string of 1s, so add the multiplicand to the left half of the product. 10: c. Beginning of a string of 1s, so subtract the multiplicand from the left half of the product. 11: d. Middle of a string of 1s, so no arithmetic operation. 2.As in the previous algorithm, shift the Product register right (arith) 1 bit. Multiplicand Product (2 x 7) Multiplicand Product (2 x -3) 0010 0000 0111 0 0010 0000 1101 0 ECE4680 ALU-II.29 2002-2-20 Booths Example: 2 x 7 (p261) mythical bit Operation Multiplicand Product|Multiplier next? 0. initial value 0010 0000 0111 0 10 -> sub 1a. P = P - m 1110 + 1110 1110 0111 0 shift P (sign ext) 1b. 0010 1111 0011 1 11 -> nop, shift 2. 0010 1111 1001 1 11 -> nop, shift 3. 0010 1111 1100 1 01 -> add 4a. 0010 + 0010 0001 1100 1 shift 4b. 0010 0000 1110 0 done ECE4680 ALU-II.30 2002-2-20 

16 . Booths Example: 2 x –3 (pp261-262) mythical bit Operation Multiplicand Product next? 0. initial value 0010 0000 1101 0 10 -> sub 1a. P = P - m 1110 + 1110 1110 1101 0 shift P (sign ext) 1b. 0010 1111 0110 1 01 -> add + 0010 2a. 0001 0110 1 shift P 2b. 0010 0000 1011 0 10 -> sub + 1110 3a. 0010 1110 1011 0 shift 3b. 0010 1111 0101 1 11 -> nop 4a 1111 0101 1 shift 4b. 0010 1111 1010 1 done ECE4680 ALU-II.31 2002-2-20 Summary °Instruction Set drives the ALU design °Shifter: success refinement from 1/bit at a time shift register to barrel shifter °Multiply: successive refinement to see final design • 32-bit Adder, 64-bit shift register, 32-bit Multiplicand Register • Booth’s algorithm to handle signed multiplies °There are algorithms that calculate many bits of multiply per cycle °What’s Missing from MIPS is Divide & Floating Point Arithmetic: Next time the Pentium Bug ECE4680 ALU-II.32 2002-2-20