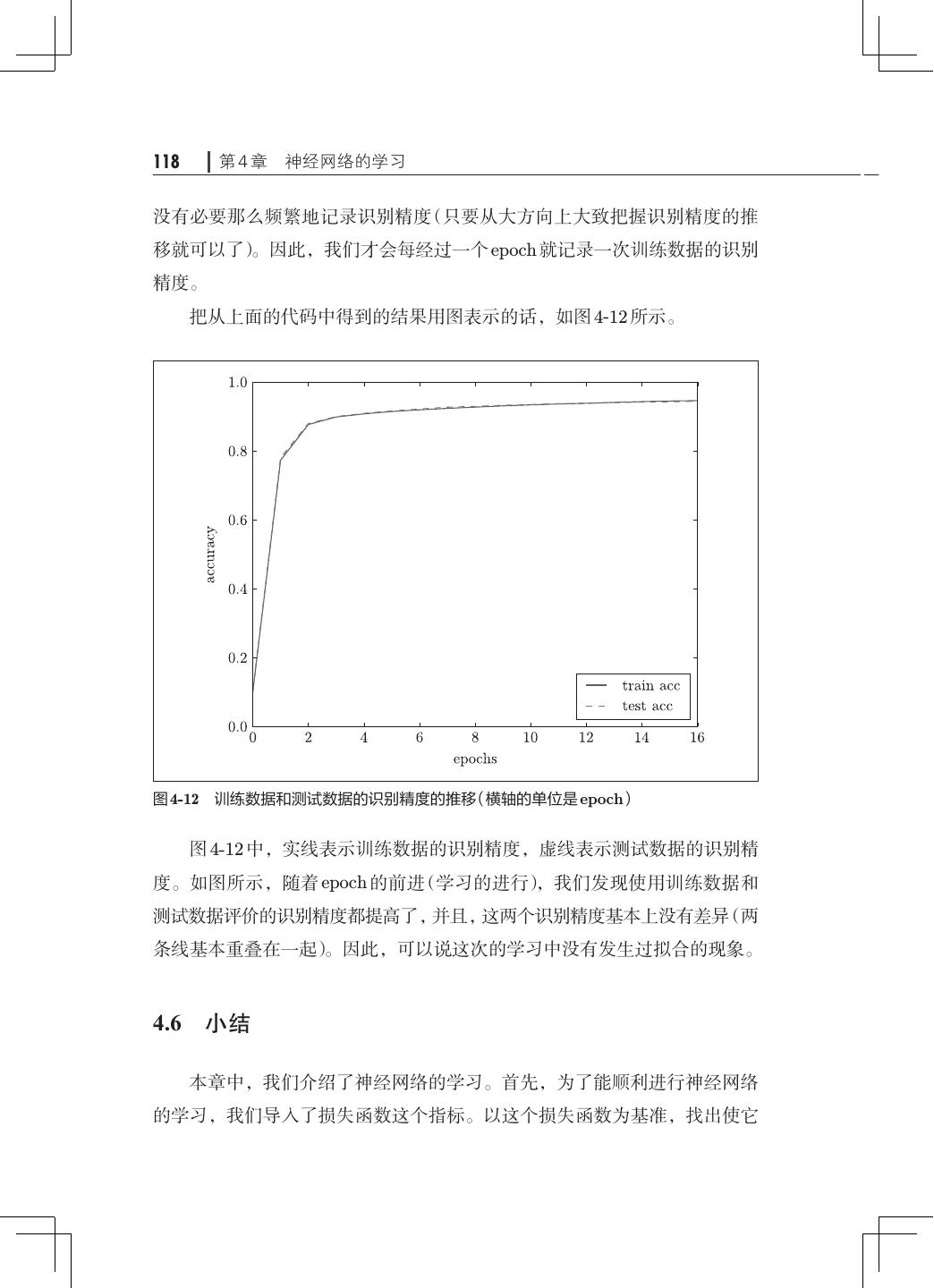
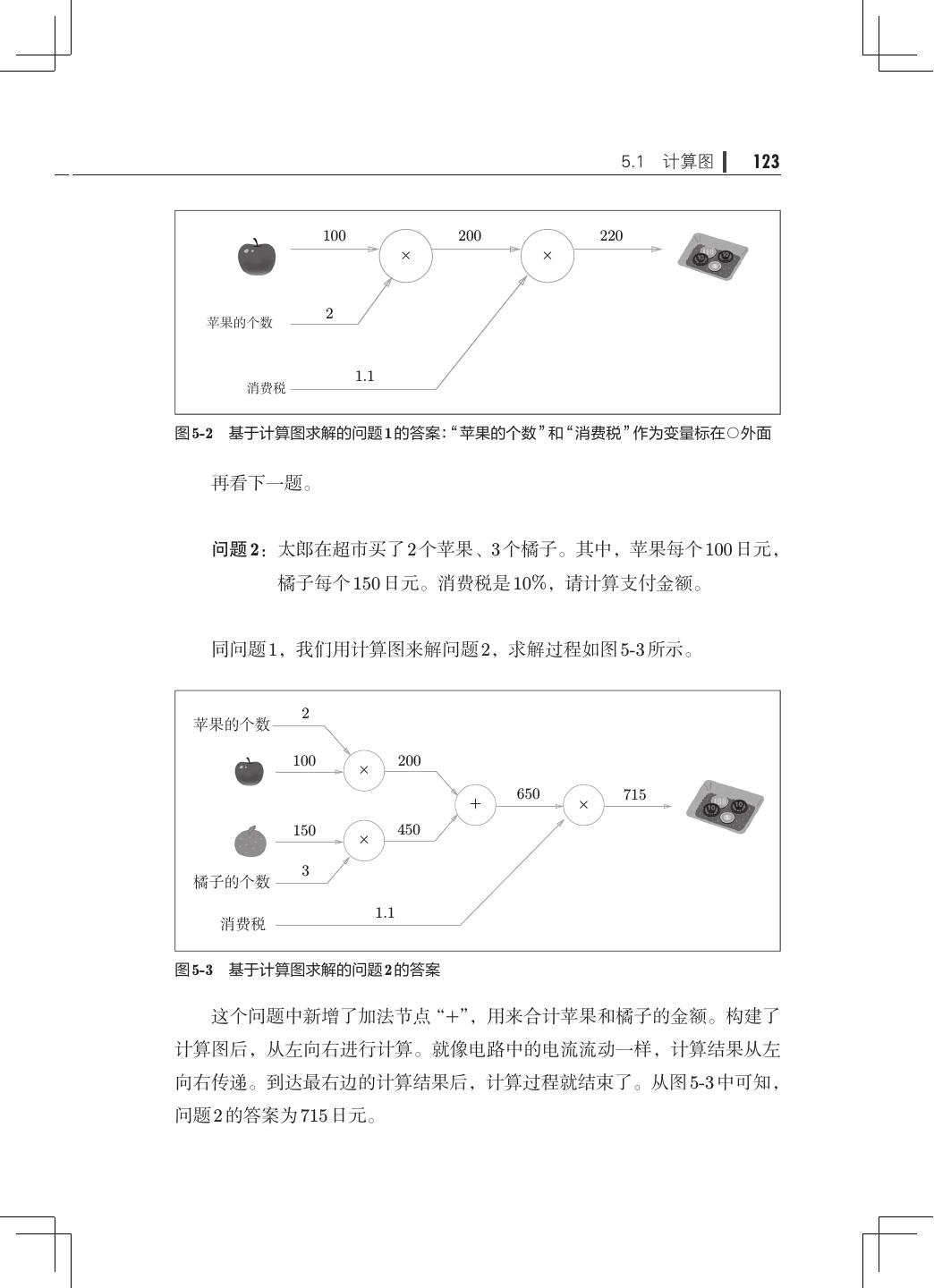
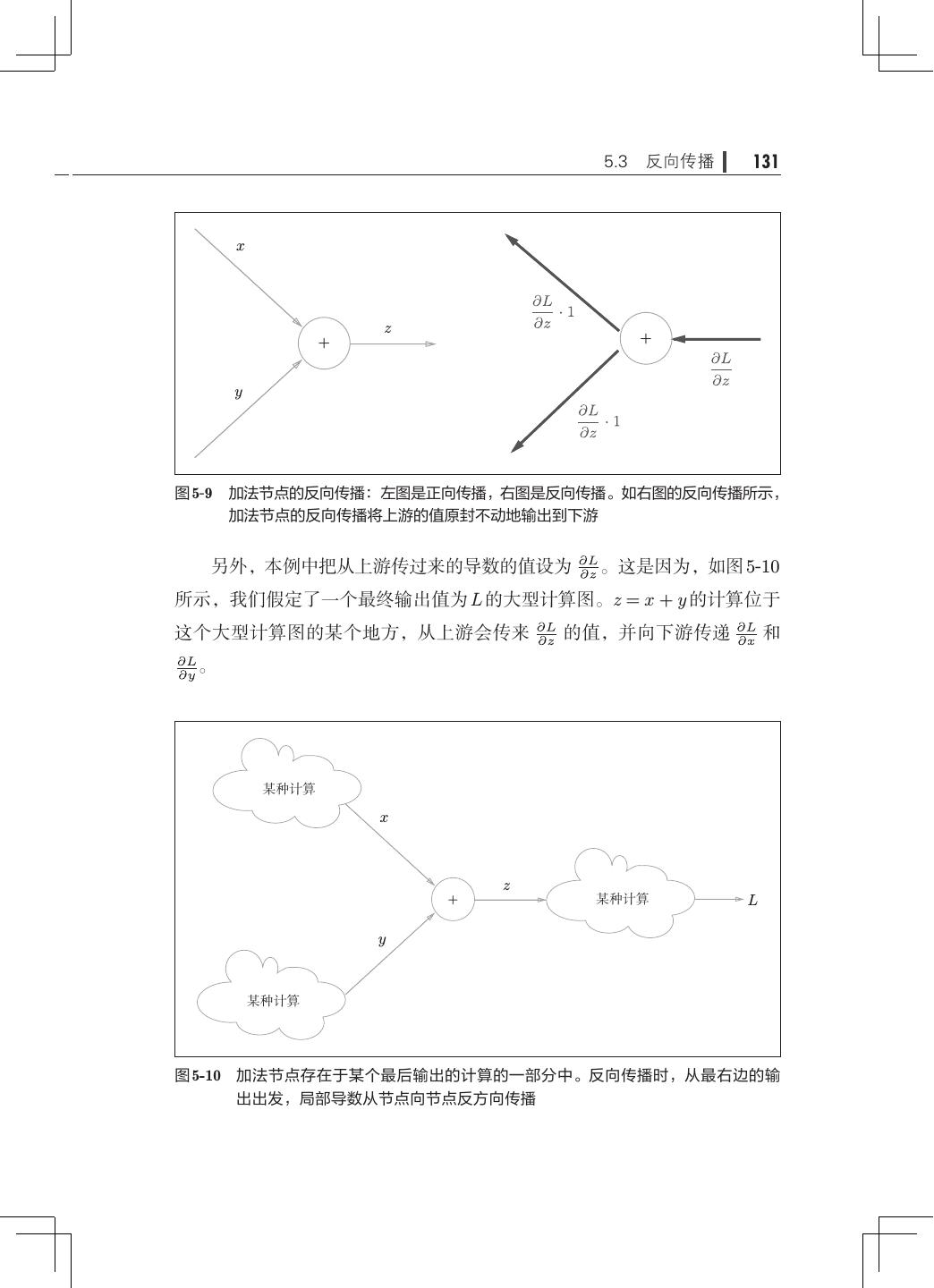
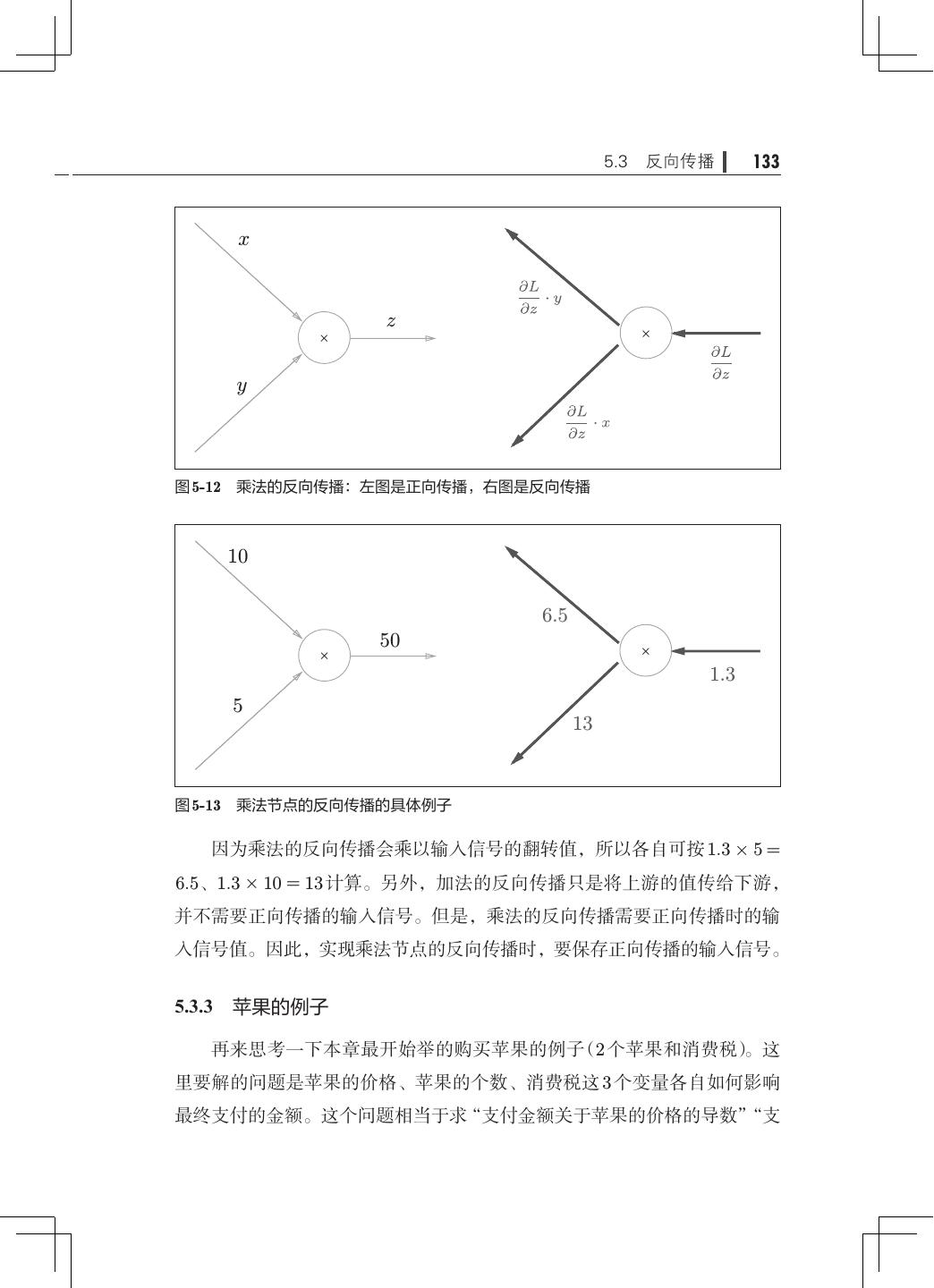
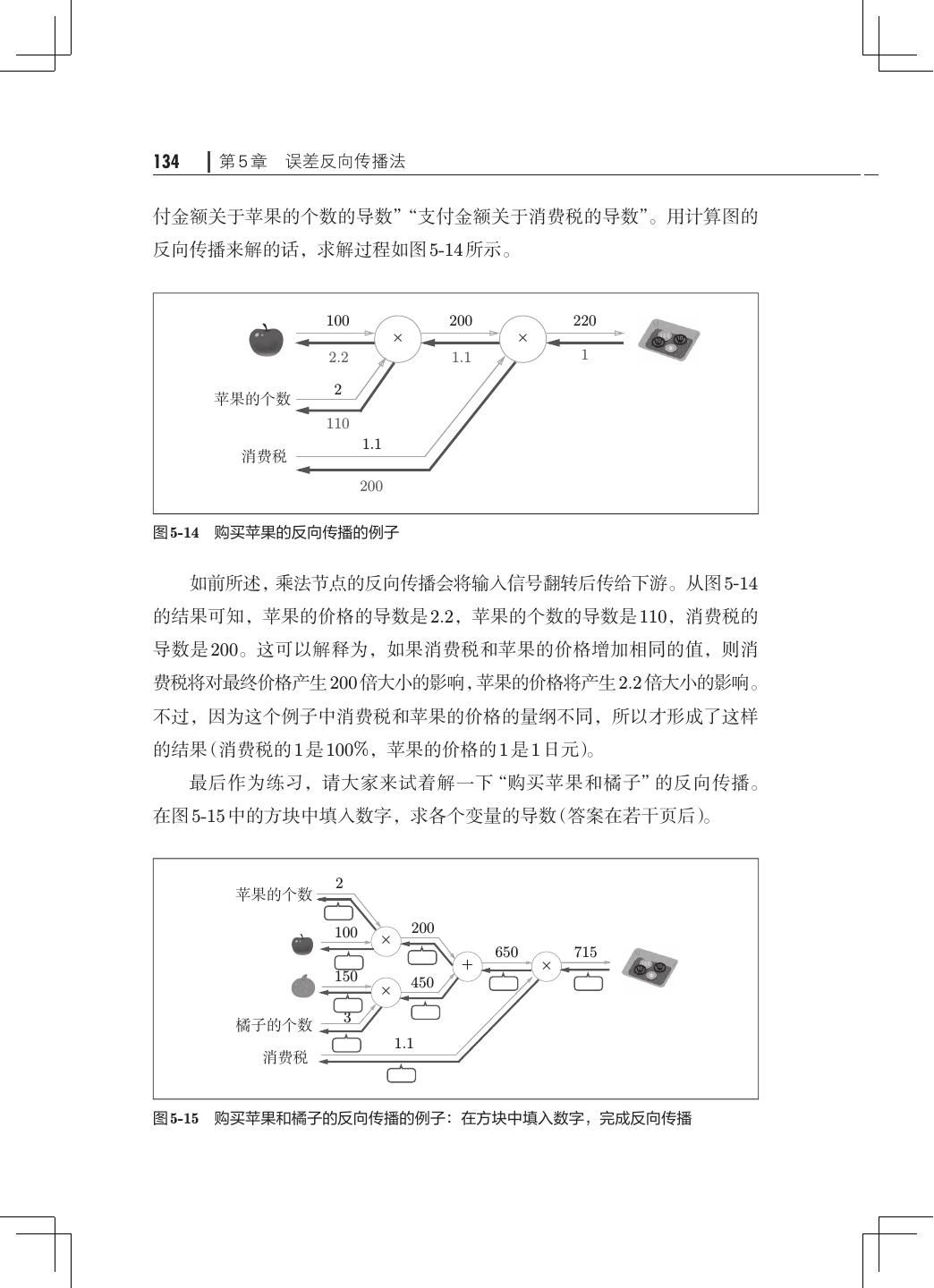
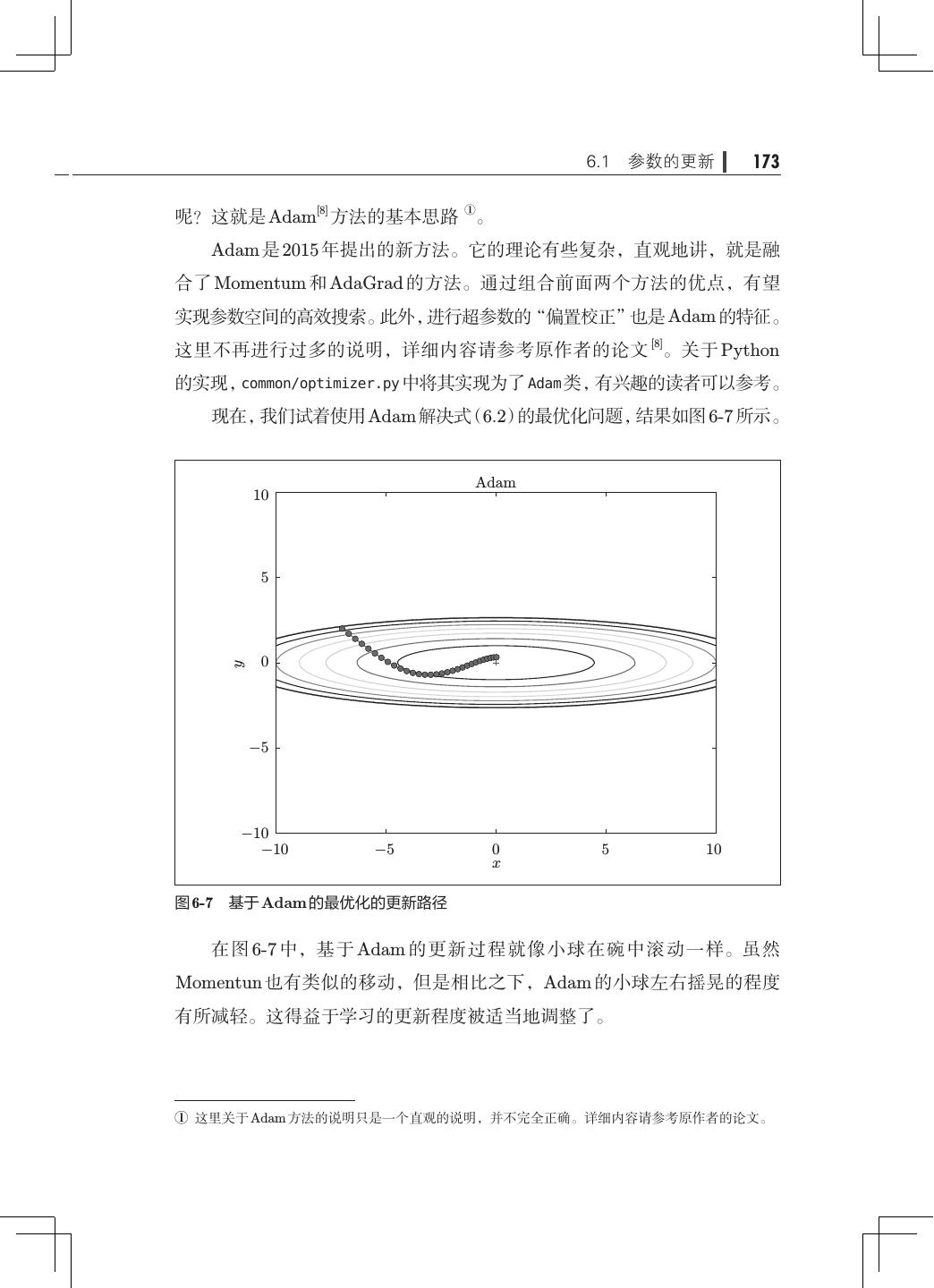
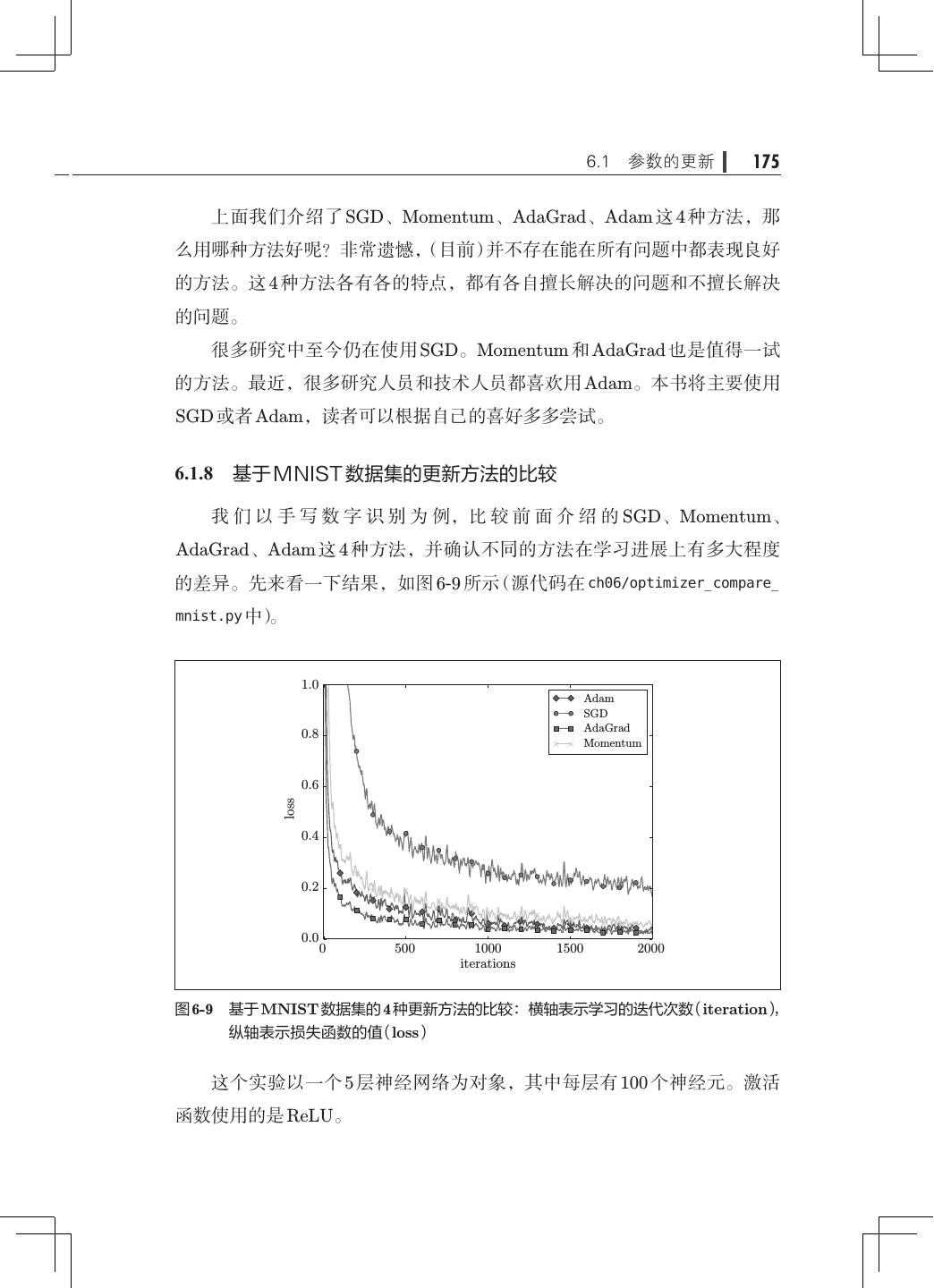
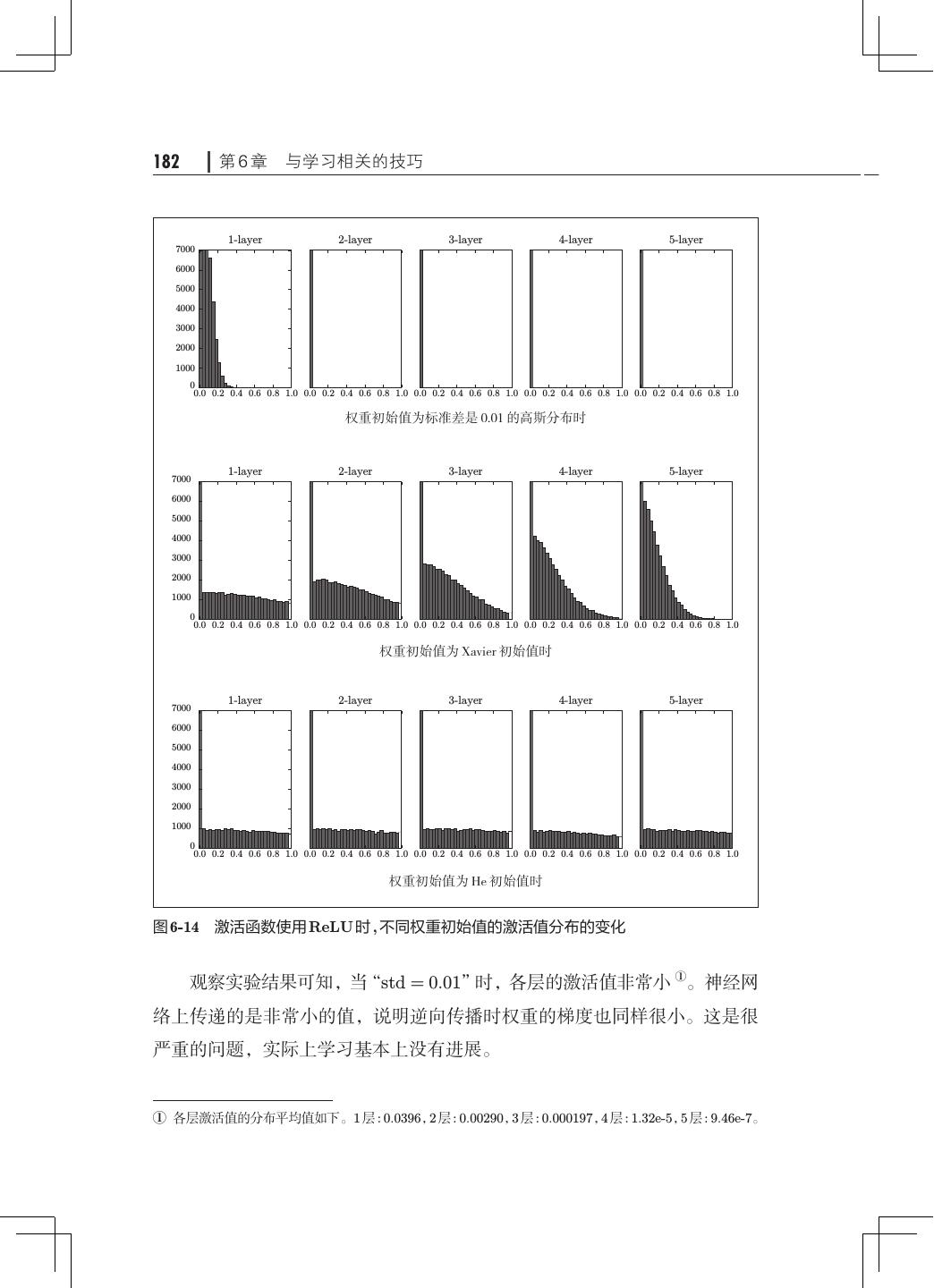
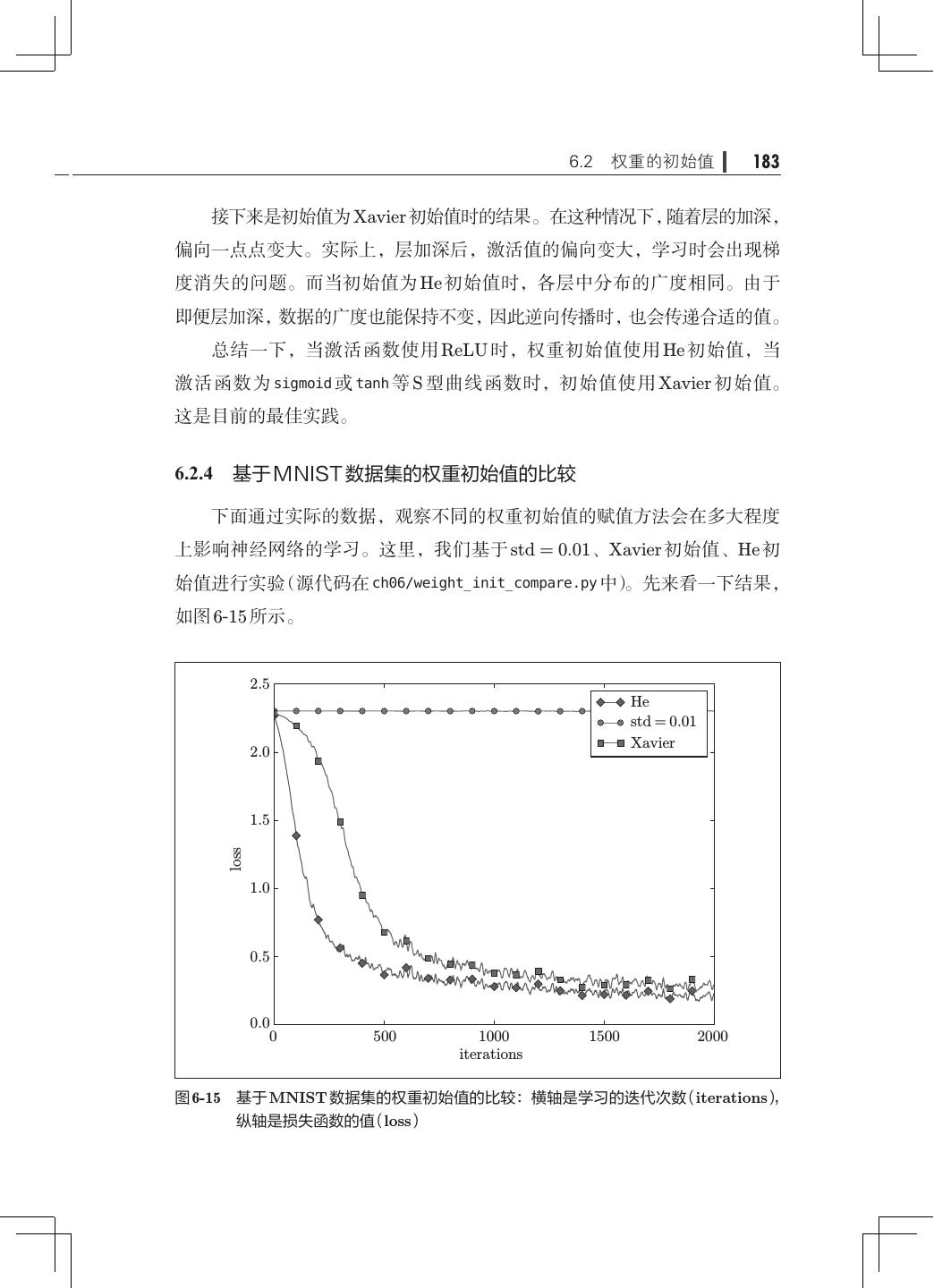
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
深度学习入门--基于Python的理论与实现
展开查看详情
1 .
2 .
3 .图灵社区的电子书没有采用专有客户 端,您可以在任意设备上,用自己喜 欢的浏览器和PDF阅读器进行阅读。 但您购买的电子书仅供您个人使用, 未经授权,不得进行传播。 我们愿意相信读者具有这样的良知和 觉悟,与我们共同保护知识产权。 如果购买者有侵权行为,我们可能对 该用户实施包括但不限于关闭该帐号 等维权措施,并可能追究法律责任。
4 .图灵程序设计丛书 深度学习入门 基于 Python 的理论与实现 Deep Learning from Scratch [日]斋藤康毅 著 陆宇杰 译 Beijing・Boston・Farnham・Sebastopol・Tokyo O’Reilly Japan, Inc. 授权人民邮电出版社出版 人民邮电出版社 北 京
5 . 图书在版编目(CIP)数据 深度学习入门 : 基于Python的理论与实现 / (日) 斋藤康毅著 ; 陆宇杰译. -- 北京 : 人民邮电出版社, 2018.7 (图灵程序设计丛书) ISBN 978-7-115-48558-8 Ⅰ. ①深… Ⅱ. ①斋… ②陆… Ⅲ. ①软件工具-程 序设计 Ⅳ. ①TP311.561 中国版本图书馆CIP数据核字(2018)第112509号 内 容 提 要 本书是深度学习真正意义上的入门书,深入浅出地剖析了深度学习的原理和相关技术。 书中使用 Python 3,尽量不依赖外部库或工具,带领读者从零创建一个经典的深度学习网 络,使读者在此过程中逐步理解深度学习。书中不仅介绍了深度学习和神经网络的概念、 特征等基础知识,对误差反向传播法、卷积神经网络等也有深入讲解,此外还介绍了学 习相关的实用技巧,自动驾驶、图像生成、强化学习等方面的应用,以及为什么加深层 可以提高识别精度等“为什么”的问题。 本书适合深度学习初学者阅读,也可作为高校教材使用。 ◆ 著 [日]斋藤康毅 译 陆宇杰 责任编辑 杜晓静 执行编辑 刘香娣 责任印制 周昇亮 ◆ 人民邮电出版社出版发行 北京市丰台区成寿寺路 11 号 邮编 100164 电子邮件 315@ptpress.com.cn 网址 http://www.ptpress.com.cn 北京 印刷 ◆ 开本:880×1230 1/32 印张:9.625 字数:300 千字 2018 年 7 月第 1 版 印数:1 - 4 000 册 2018 年 7 月北京第 1 次印刷 著作权合同登记号 图字:01-2017-0526 号 定价:59.00 元 读者服务热线:(010)51095186转 600 印装质量热线:(010)81055316 反盗版热线:(010)81055315 广告经营许可证:京东工商广登字 20170147 号
6 . 版权声明 Copyright © 2016 Koki Saitoh, O’Reilly Japan, Inc. Posts and Telecommunications Press, 2018. Authorized translation of the Japanese edition of “Deep Learning from Scratch” © 2016 O’ Reilly Japan, Inc. This translation is published and sold by permission of O’ Reilly Japan, Inc., the owner of all rights to publish and sell the same. 日文原版由 O’Reilly Japan, Inc. 出版,2016。 简体中文版由人民邮电出版社出版,2018。日文原版的翻译得到 O’Reilly Japan, Inc. 的授权。此简体中文版的出版和销售得到出版权和销售权的所有 者——O’Reilly Japan, Inc. 的许可。 版权所有,未得书面许可,本书的任何部分和全部不得以任何形式重制。
7 .O’Reilly Media, Inc.介绍 O’Reilly Media 通过图书、杂志、在线服务、调查研究和会议等方式传播创新知识。 自 1978 年开始,O’Reilly 一直都是前沿发展的见证者和推动者。超级极客们正在开 创着未来,而我们关注真正重要的技术趋势——通过放大那些“细微的信号”来刺激 社会对新科技的应用。作为技术社区中活跃的参与者,O’Reilly 的发展充满了对创新 的倡导、创造和发扬光大。 O’Reilly 为软件开发人员带来革命性的“动物书”;创建第一个商业网站(GNN);组 织了影响深远的开放源代码峰会,以至于开源软件运动以此命名;创立了 Make 杂志, 从而成为 DIY 革命的主要先锋;公司一如既往地通过多种形式缔结信息与人的纽带。 O’Reilly 的会议和峰会集聚了众多超级极客和高瞻远瞩的商业领袖,共同描绘出开创 新产业的革命性思想。作为技术人士获取信息的选择,O’Reilly 现在还将先锋专家的 知识传递给普通的计算机用户。无论是通过书籍出版、在线服务或者面授课程,每一 项 O’Reilly 的产品都反映了公司不可动摇的理念——信息是激发创新的力量。 业界评论 “O’Reilly Radar 博客有口皆碑。” ——Wired “O’Reilly 凭借一系列(真希望当初我也想到了)非凡想法建立了数百万美元的业务。” ——Business 2.0 “O’Reilly Conference 是聚集关键思想领袖的绝对典范。” ——CRN “一本 O’Reilly 的书就代表一个有用、有前途、需要学习的主题。” ——Irish Times “Tim 是位特立独行的商人,他不光放眼于最长远、最广阔的视野,并且切实地按照 Yogi Berra 的建议去做了: ‘如果你在路上遇到岔路口,走小路(岔路)。’回顾过去, Tim 似乎每一次都选择了小路,而且有几次都是一闪即逝的机会,尽管大路也不错。” ——Linux Journal
8 . 目录 译者序······················································· xiii 前言························································· xv 第 1 章 Python 入门· ··········································· 1 1.1 Python 是什么· ········································· 1 1.2 Python 的安装 · ········································· 2 1.2.1 Python 版本· ····································· 2 1.2.2 使用的外部库· ···································· 2 1.2.3 Anaconda 发行版· ································· 3 1.3 Python 解释器· ········································· 4 1.3.1 算术计算 ········································· 4 1.3.2 数据类型 ········································· 5 1.3.3 变量············································· 5 1.3.4 列表············································· 6 1.3.5 字典············································· 7 1.3.6 布尔型··········································· 7 1.3.7 if 语句· ·········································· 8 1.3.8 for 语句·········································· 8 1.3.9 函数············································· 9 1.4 Python 脚本文件· ······································· 9
9 .vi 目录 1.4.1 保存为文件······································· 9 1.4.2 类· ············································ 10 1.5 NumPy · ·············································· 11 1.5.1 导入 NumPy· ···································· 11 1.5.2 生成 NumPy 数组· ································ 12 1.5.3 NumPy 的算术运算······························· 12 1.5.4 NumPy 的 N 维数组· ······························ 13 1.5.5 广播············································ 14 1.5.6 访问元素········································ 15 1.6 Matplotlib············································· 16 1.6.1 绘制简单图形· ··································· 16 1.6.2 pyplot 的功能· ··································· 17 1.6.3 显示图像········································ 18 1.7 小结·················································· 19 第 2 章 感知机················································ 21 2.1 感知机是什么· ········································· 21 2.2 简单逻辑电路· ········································· 23 2.2.1 与门············································ 23 2.2.2 与非门和或门· ··································· 23 2.3 感知机的实现· ········································· 25 2.3.1 简单的实现······································ 25 2.3.2 导入权重和偏置· ································· 26 2.3.3 使用权重和偏置的实现· ··························· 26 2.4 感知机的局限性· ······································· 28 2.4.1 异或门·········································· 28 2.4.2 线性和非线性· ··································· 30 2.5 多层感知机· ··········································· 31 2.5.1 已有门电路的组合· ······························· 31
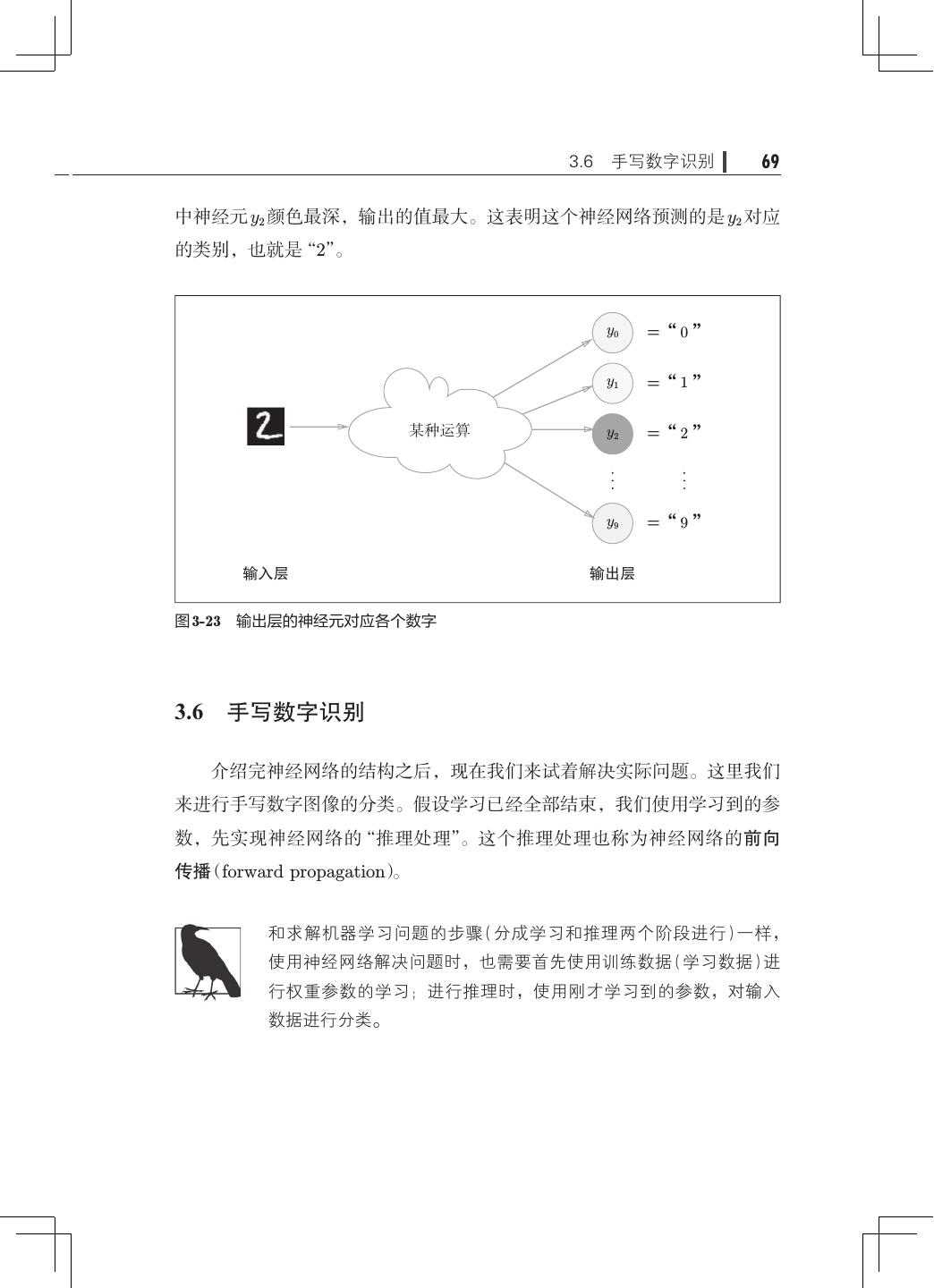
10 . 目录 vii 2.5.2 异或门的实现· ··································· 33 2.6 从与非门到计算机· ····································· 35 2.7 小结·················································· 36 第 3 章 神经网络·············································· 37 3.1 从感知机到神经网络· ··································· 37 3.1.1 神经网络的例子· ································· 37 3.1.2 复习感知机······································ 38 3.1.3 激活函数登场· ··································· 40 3.2 激活函数·············································· 42 3.2.1 sigmoid 函数· ···································· 42 3.2.2 阶跃函数的实现· ································· 43 3.2.3 阶跃函数的图形· ································· 44 3.2.4 sigmoid 函数的实现· ······························ 45 3.2.5 sigmoid 函数和阶跃函数的比较······················ 46 3.2.6 非线性函数······································ 48 3.2.7 ReLU 函数· ····································· 49 3.3 多维数组的运算· ······································· 50 3.3.1 多维数组········································ 50 3.3.2 矩阵乘法········································ 51 3.3.3 神经网络的内积· ································· 55 3.4 3 层神经网络的实现· ···································· 56 3.4.1 符号确认········································ 57 3.4.2 各层间信号传递的实现· ··························· 58 3.4.3 代码实现小结· ··································· 62 3.5 输出层的设计· ········································· 63 3.5.1 恒等函数和 softmax 函数· ·························· 64 3.5.2 实现 softmax 函数时的注意事项· ···················· 66 3.5.3 softmax 函数的特征· ······························ 67
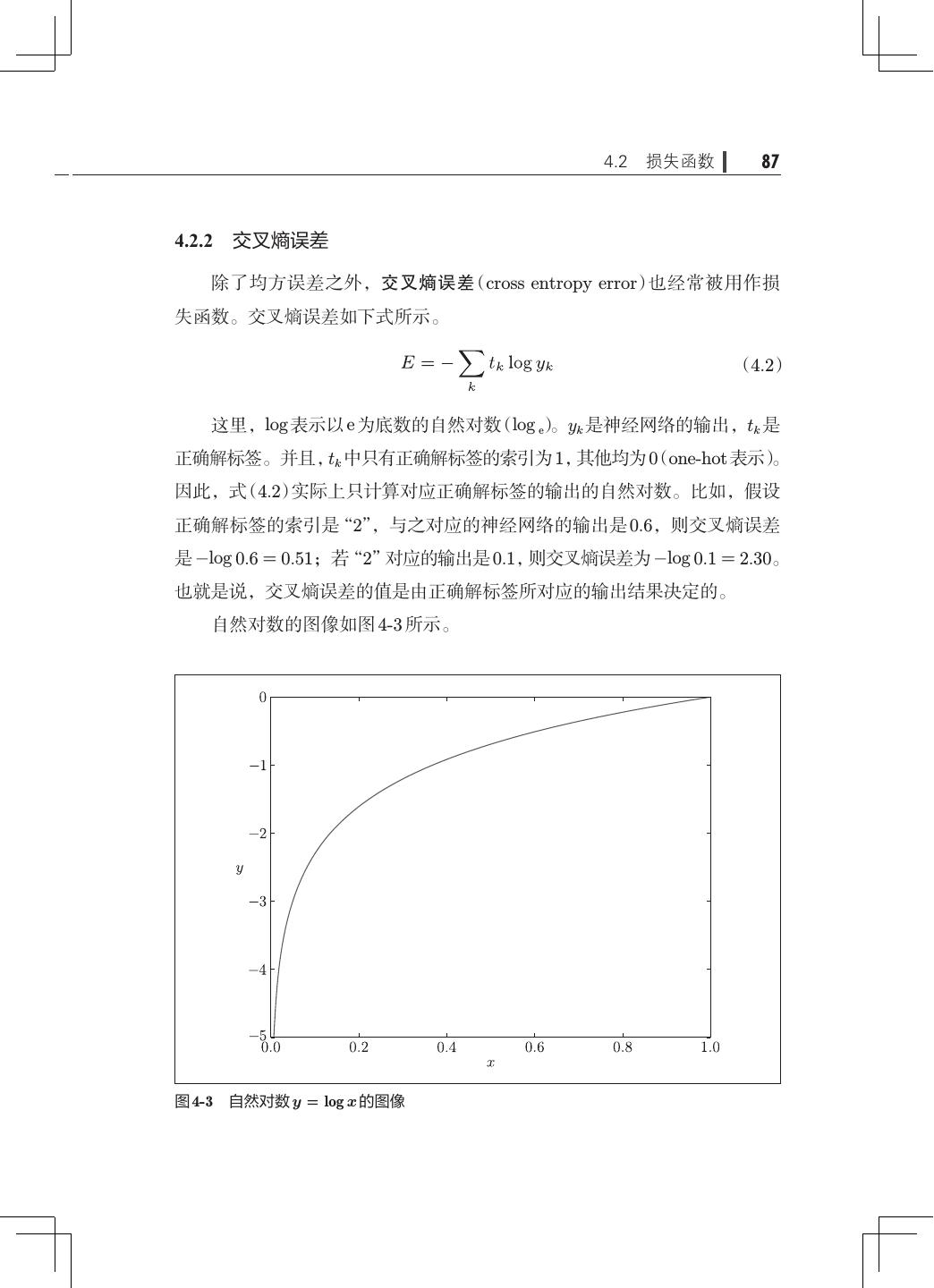
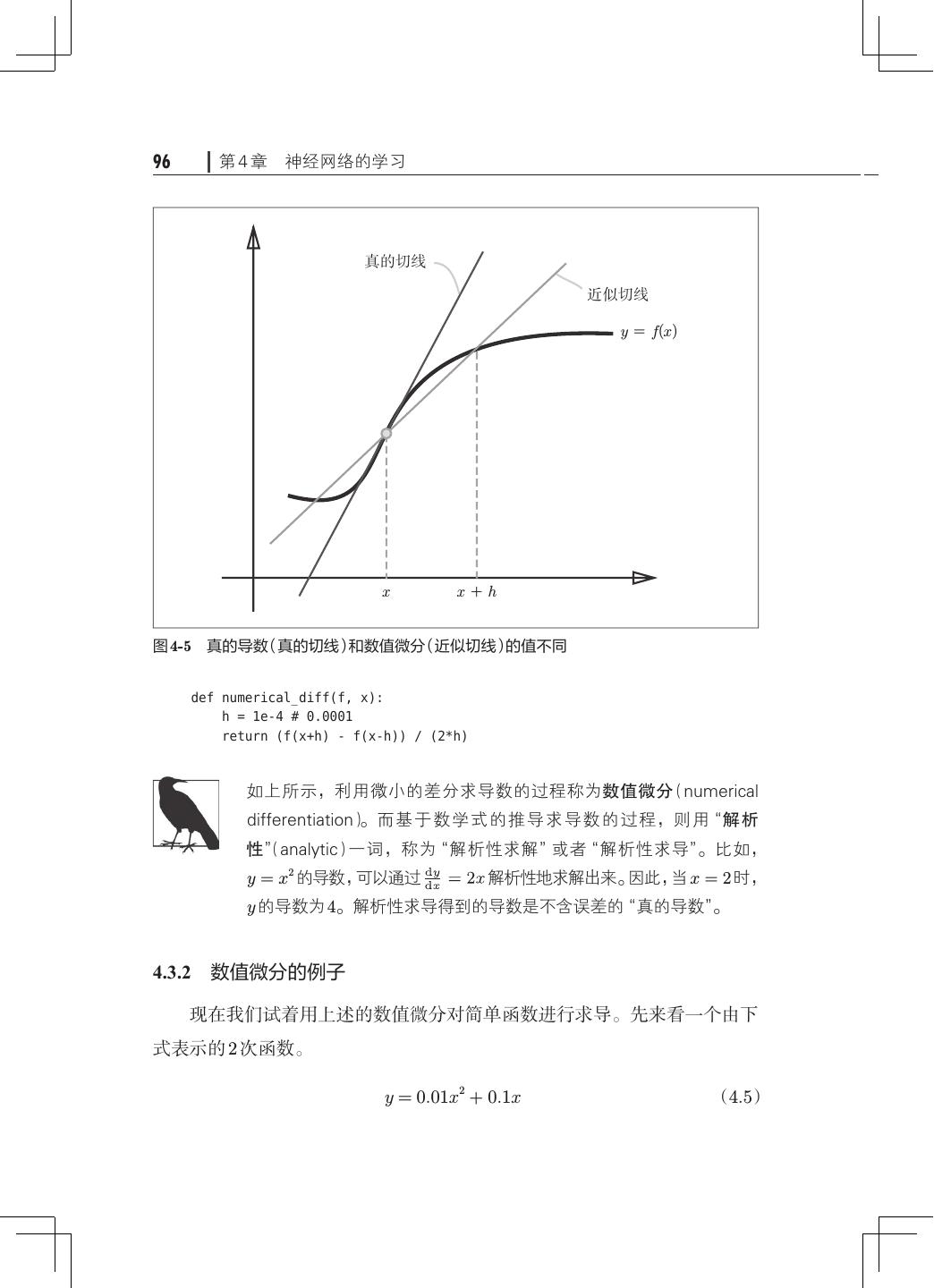
11 .viii 目录 3.5.4 输出层的神经元数量· ····························· 68 3.6 手写数字识别· ········································· 69 3.6.1 MNIST 数据集· ·································· 70 3.6.2 神经网络的推理处理· ····························· 73 3.6.3 批处理·········································· 75 3.7 小结·················································· 79 第 4 章 神经网络的学习· ······································· 81 4.1 从数据中学习· ········································· 81 4.1.1 数据驱动········································ 82 4.1.2 训练数据和测试数据· ····························· 84 4.2 损失函数·············································· 85 4.2.1 均方误差········································ 85 4.2.2 交叉熵误差······································ 87 4.2.3 mini-batch 学习· ································· 88 4.2.4 mini-batch 版交叉熵误差的实现· ···················· 91 4.2.5 为何要设定损失函数· ····························· 92 4.3 数值微分·············································· 94 4.3.1 导数············································ 94 4.3.2 数值微分的例子· ································· 96 4.3.3 偏导数·········································· 98 4.4 梯度··················································100 4.4.1 梯度法··········································102 4.4.2 神经网络的梯度· ·································106 4.5 学习算法的实现· ·······································109 4.5.1 2 层神经网络的类·································110 4.5.2 mini-batch 的实现· ·······························114 4.5.3 基于测试数据的评价· ·····························116 4.6 小结··················································118
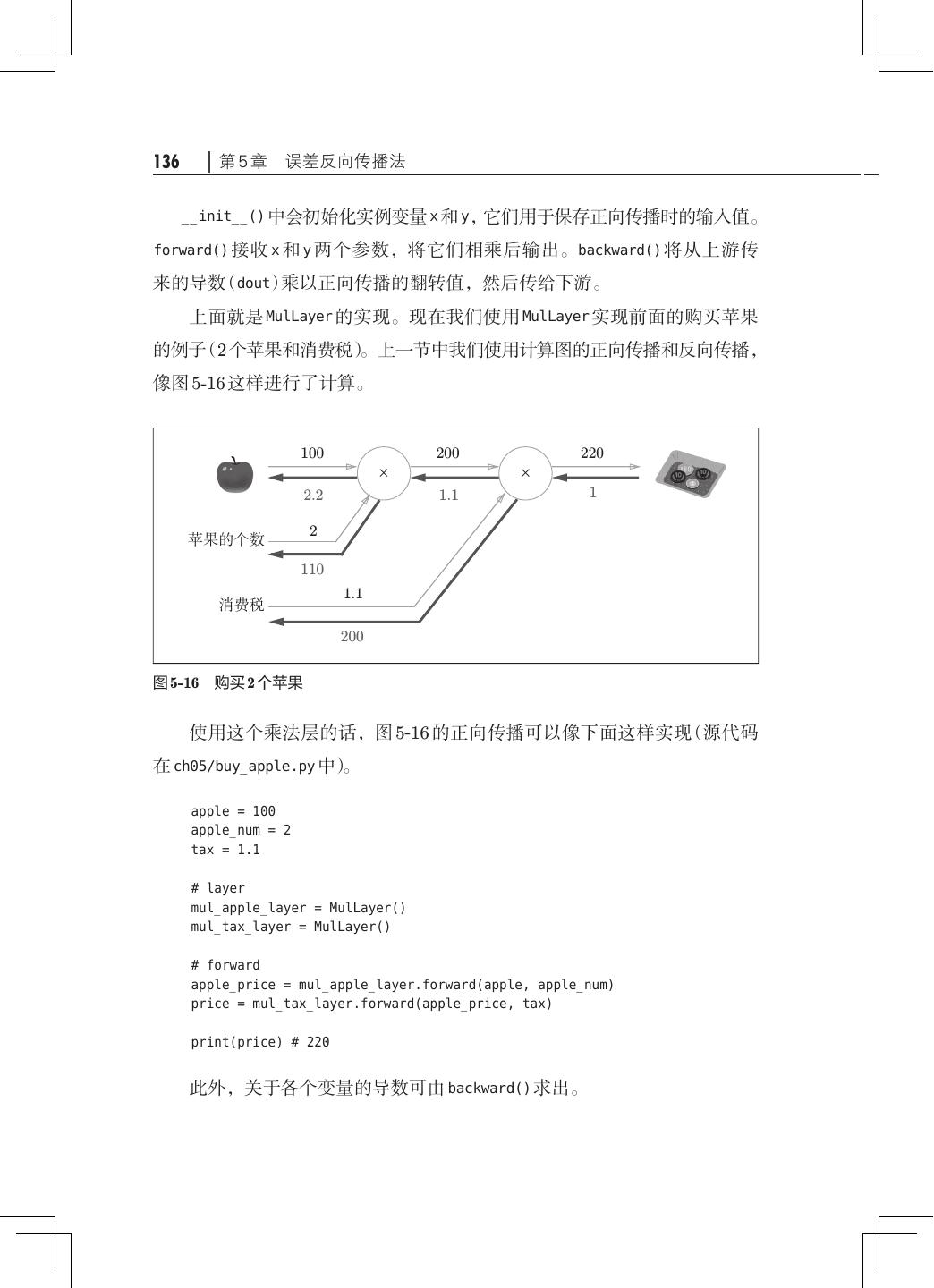
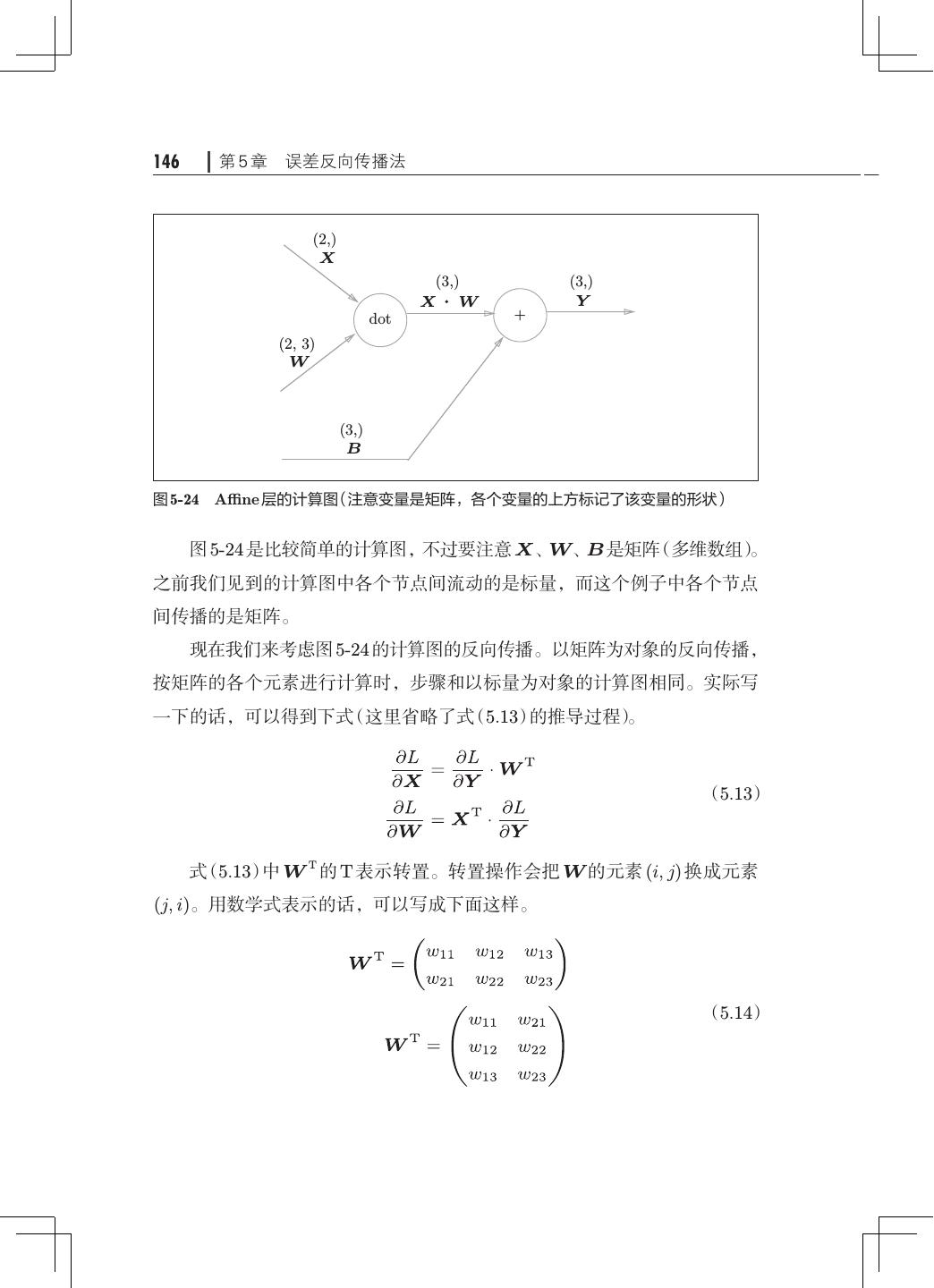
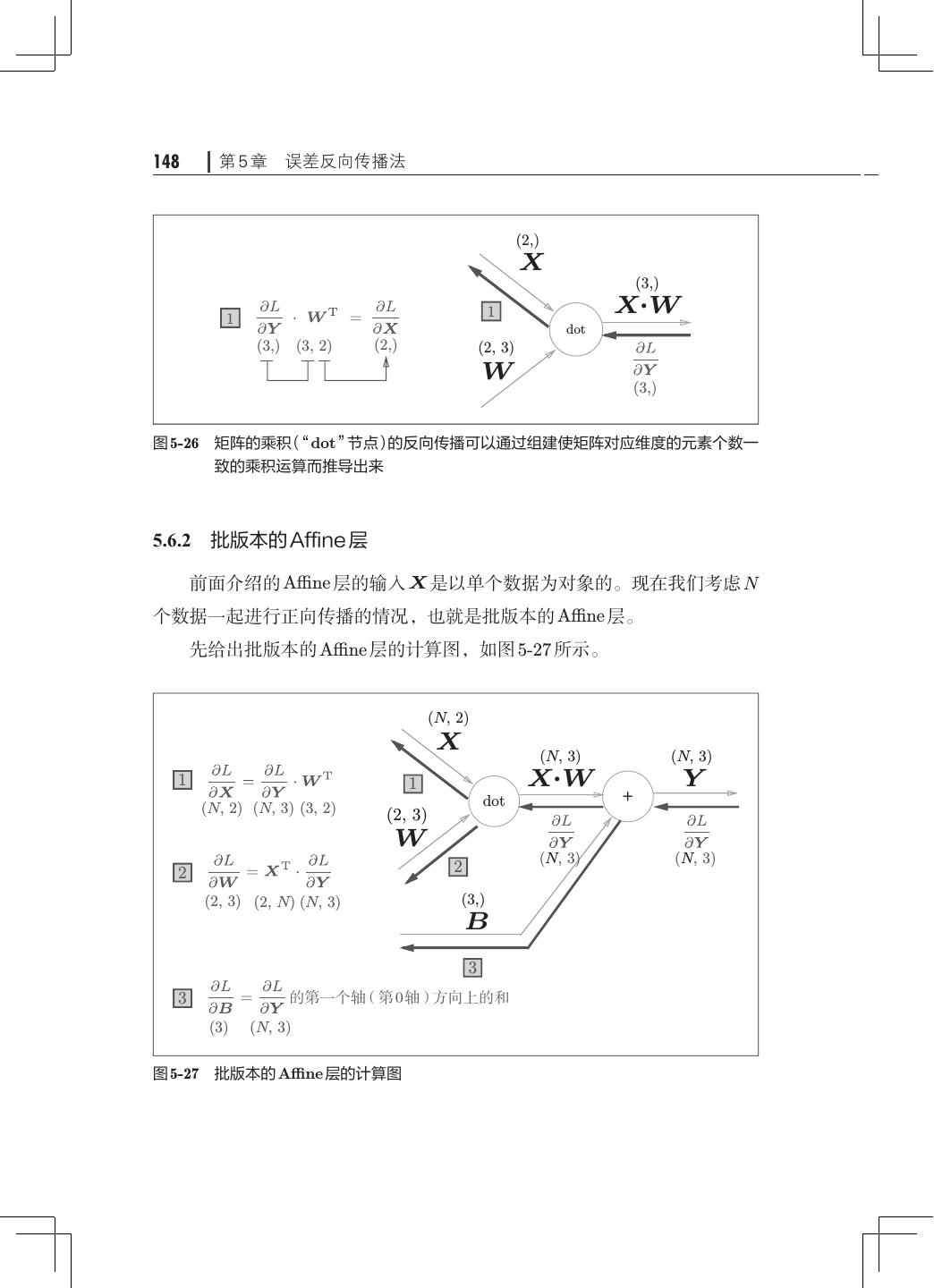
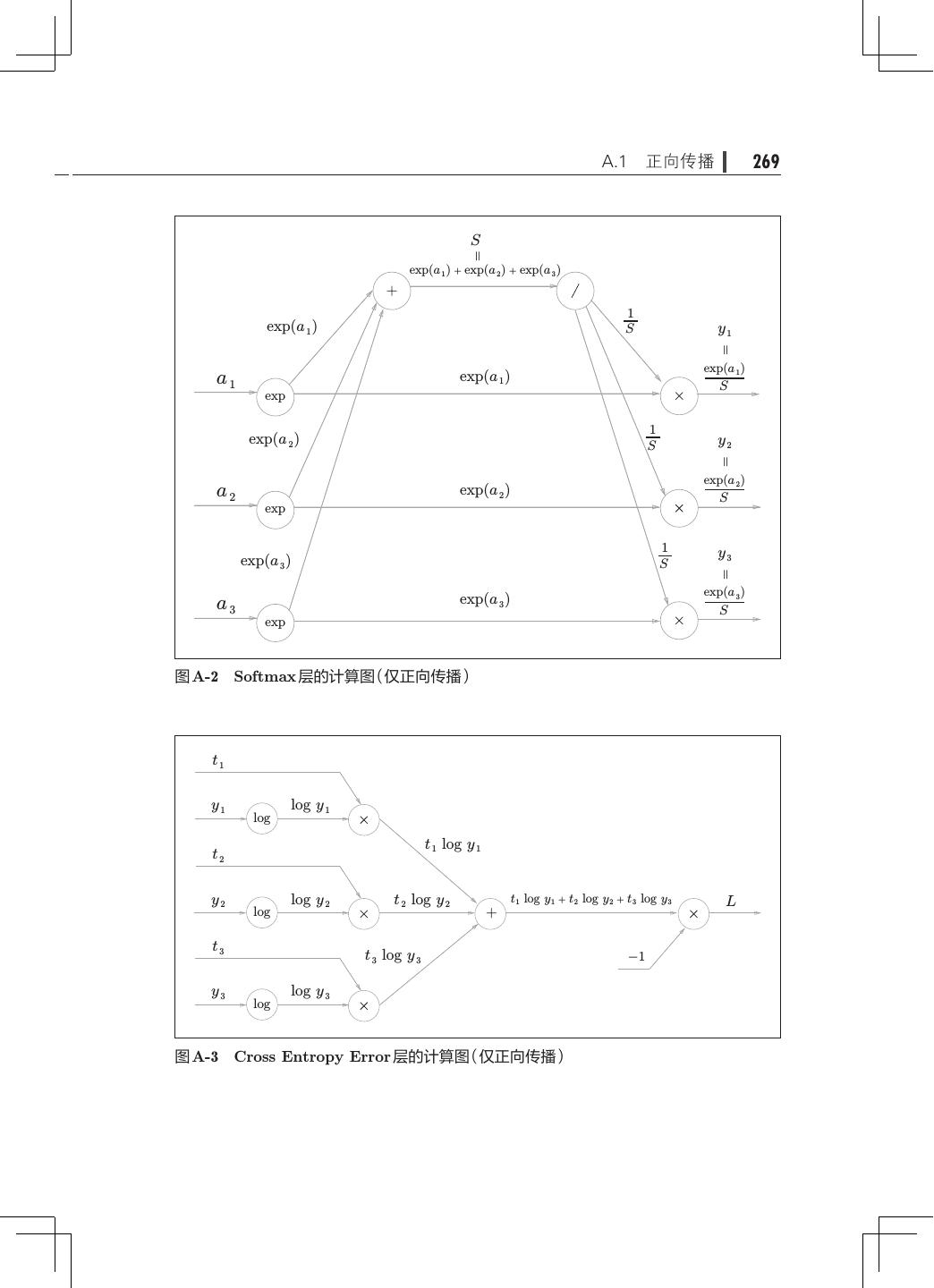
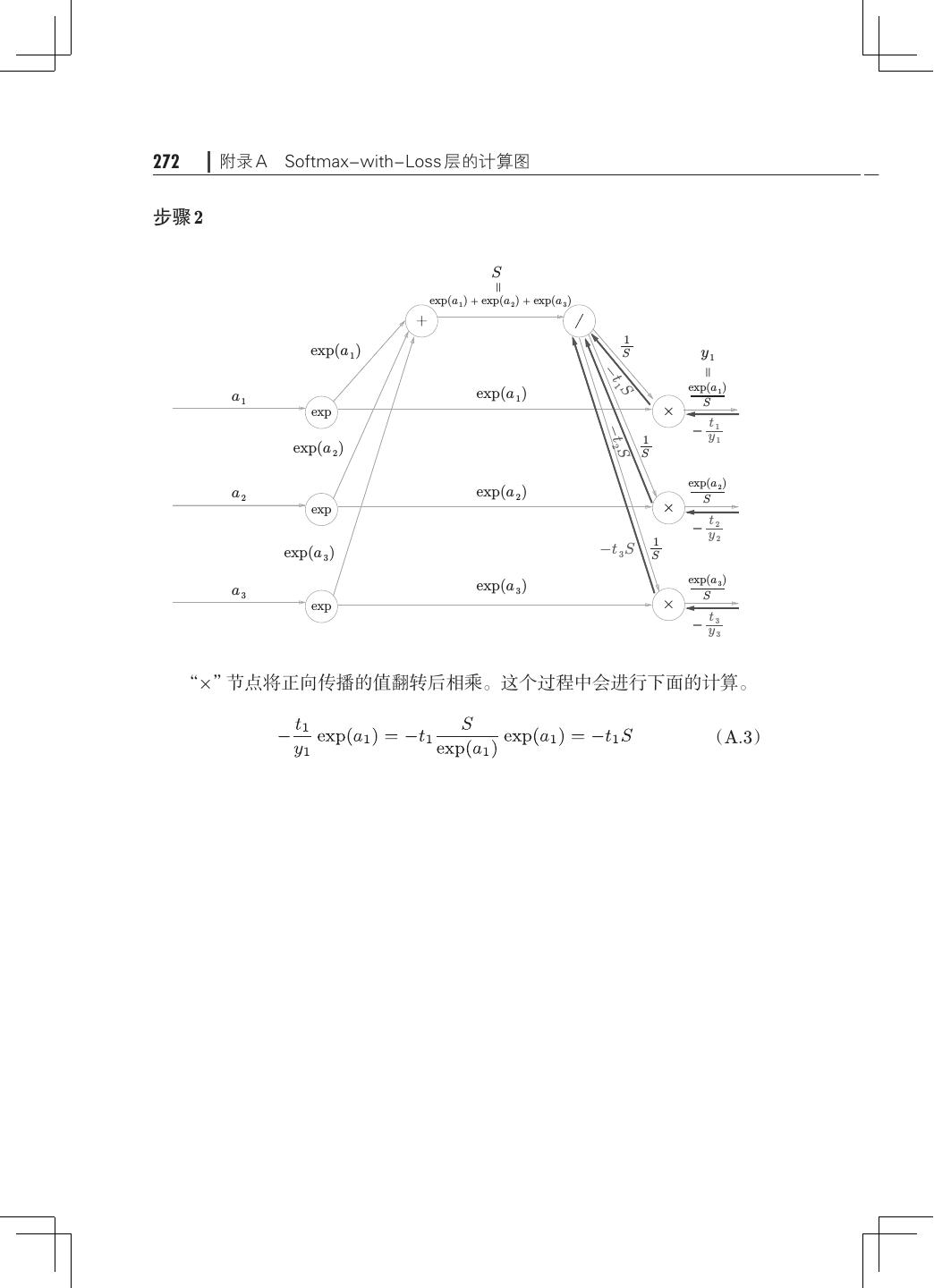
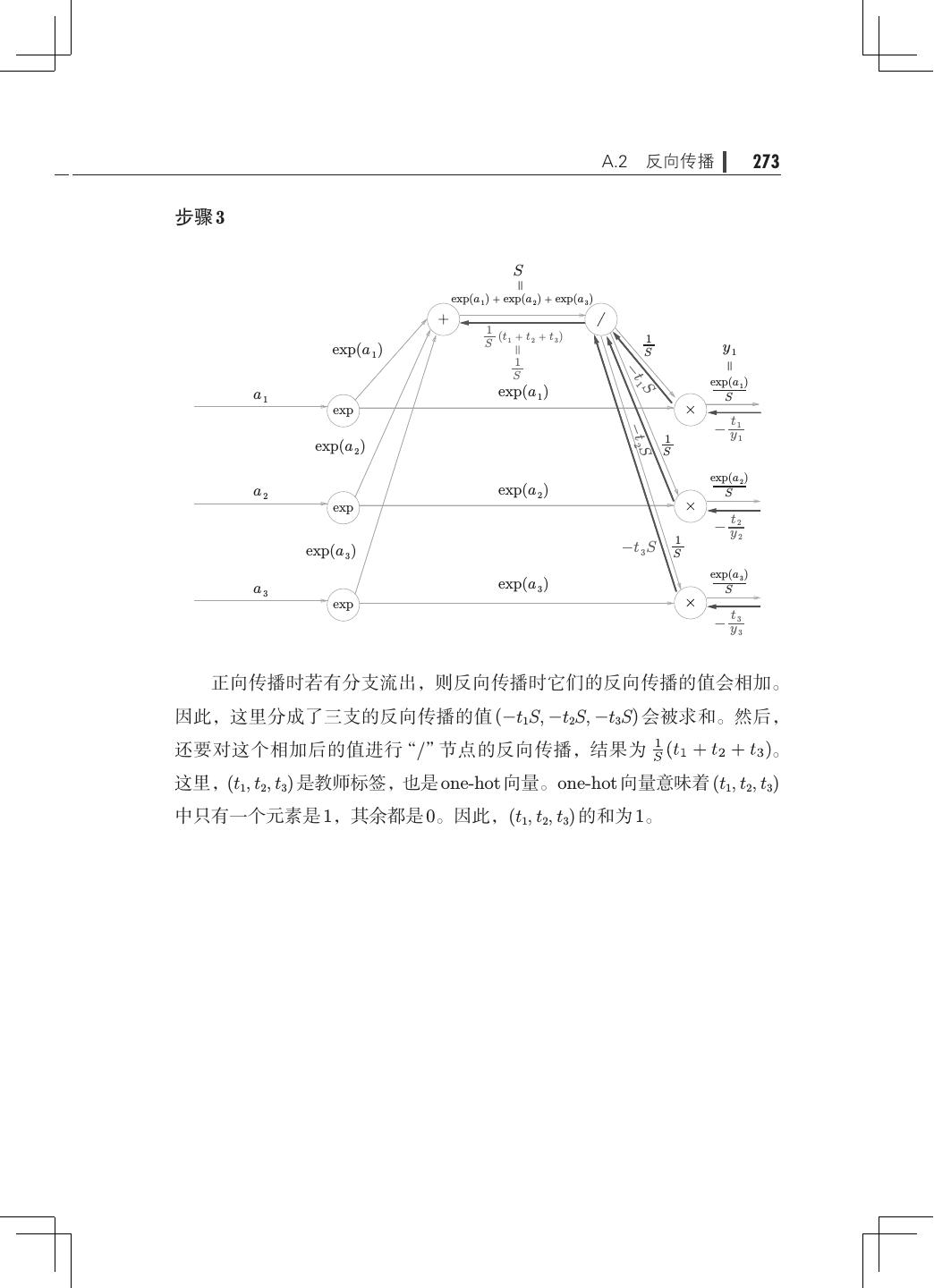
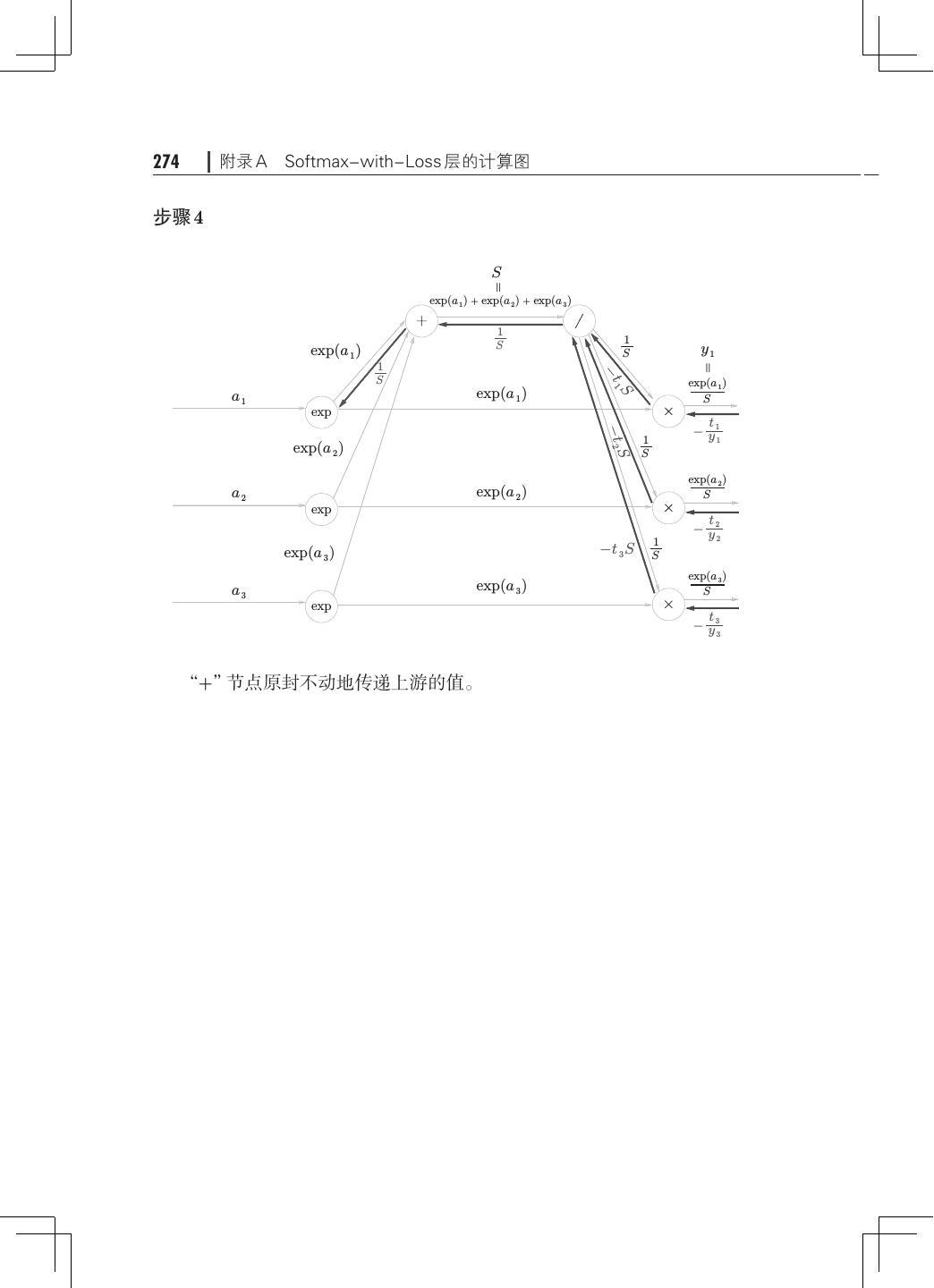
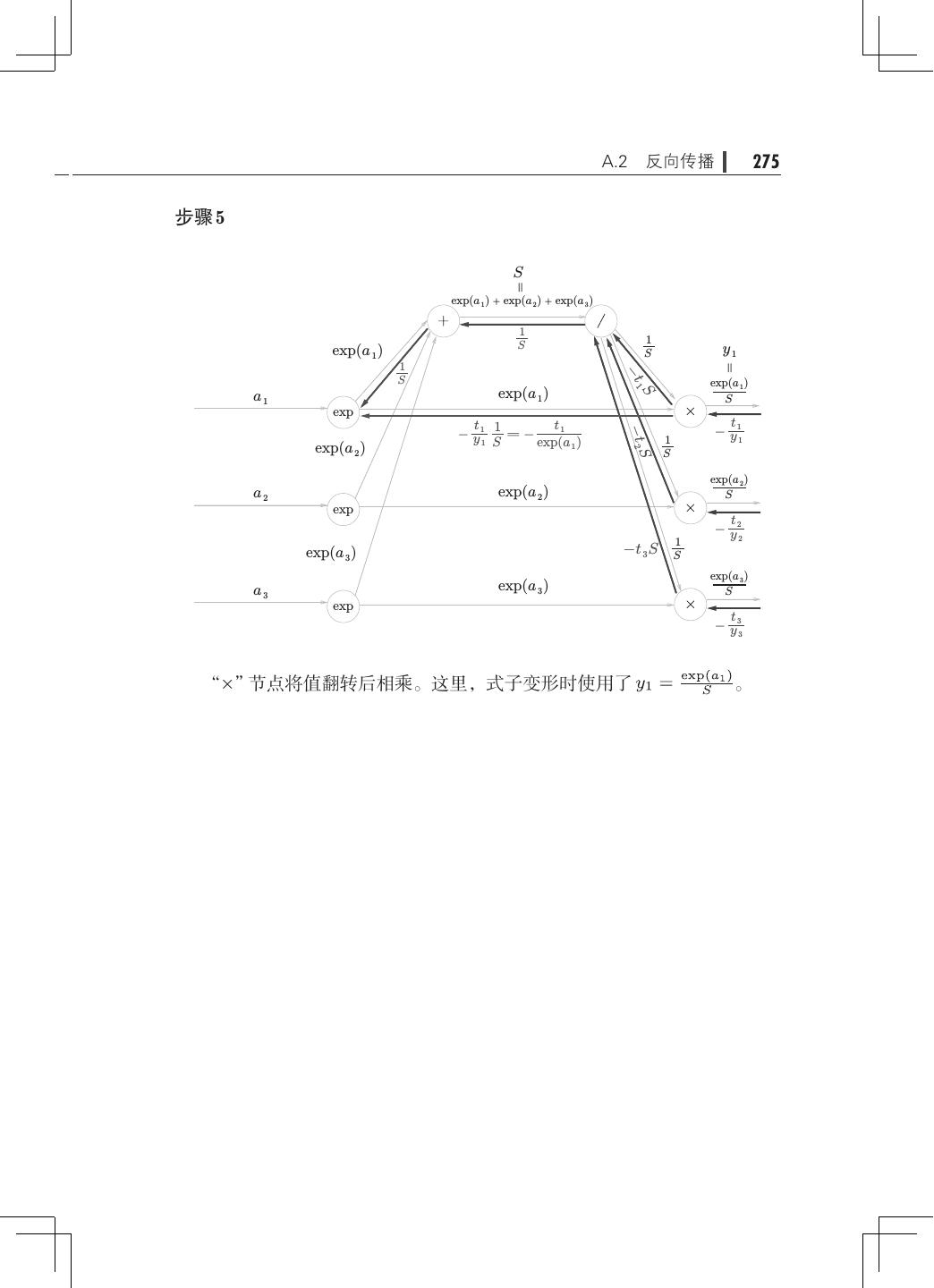
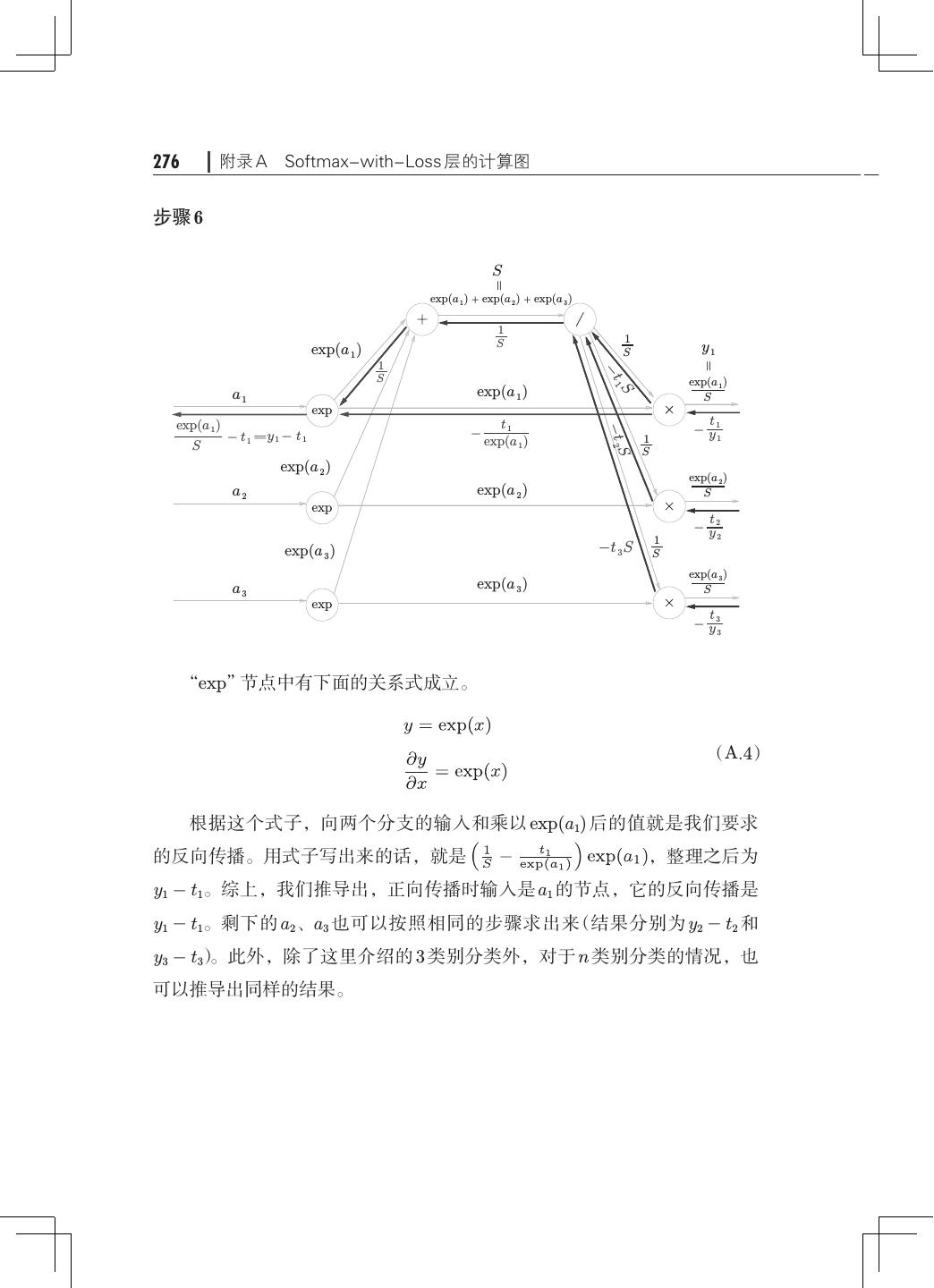
12 . 目录 ix 第 5 章 误差反向传播法· ·······································121 5.1 计算图················································121 5.1.1 用计算图求解· ···································122 5.1.2 局部计算········································124 5.1.3 为何用计算图解题· ·······························125 5.2 链式法则··············································126 5.2.1 计算图的反向传播· ·······························127 5.2.2 什么是链式法则· ·································127 5.2.3 链式法则和计算图· ·······························129 5.3 反向传播··············································130 5.3.1 加法节点的反向传播· ·····························130 5.3.2 乘法节点的反向传播· ·····························132 5.3.3 苹果的例子······································133 5.4 简单层的实现· ·········································135 5.4.1 乘法层的实现· ···································135 5.4.2 加法层的实现· ···································137 5.5 激活函数层的实现· ·····································139 5.5.1 ReLU 层· ······································· 139 5.5.2 Sigmoid 层·······································141 5.6 Affine/Softmax 层的实现·································144 5.6.1 Affine 层· ·······································144 5.6.2 批版本的 Affine 层· ······························· 148 5.6.3 Softmax-with-Loss 层· ····························150 5.7 误差反向传播法的实现· ································· 154 5.7.1 神经网络学习的全貌图· ···························154 5.7.2 对应误差反向传播法的神经网络的实现 155 · ·············· 5.7.3 误差反向传播法的梯度确认 ·························158 5.7.4 使用误差反向传播法的学习·························159 5.8 小结··················································161
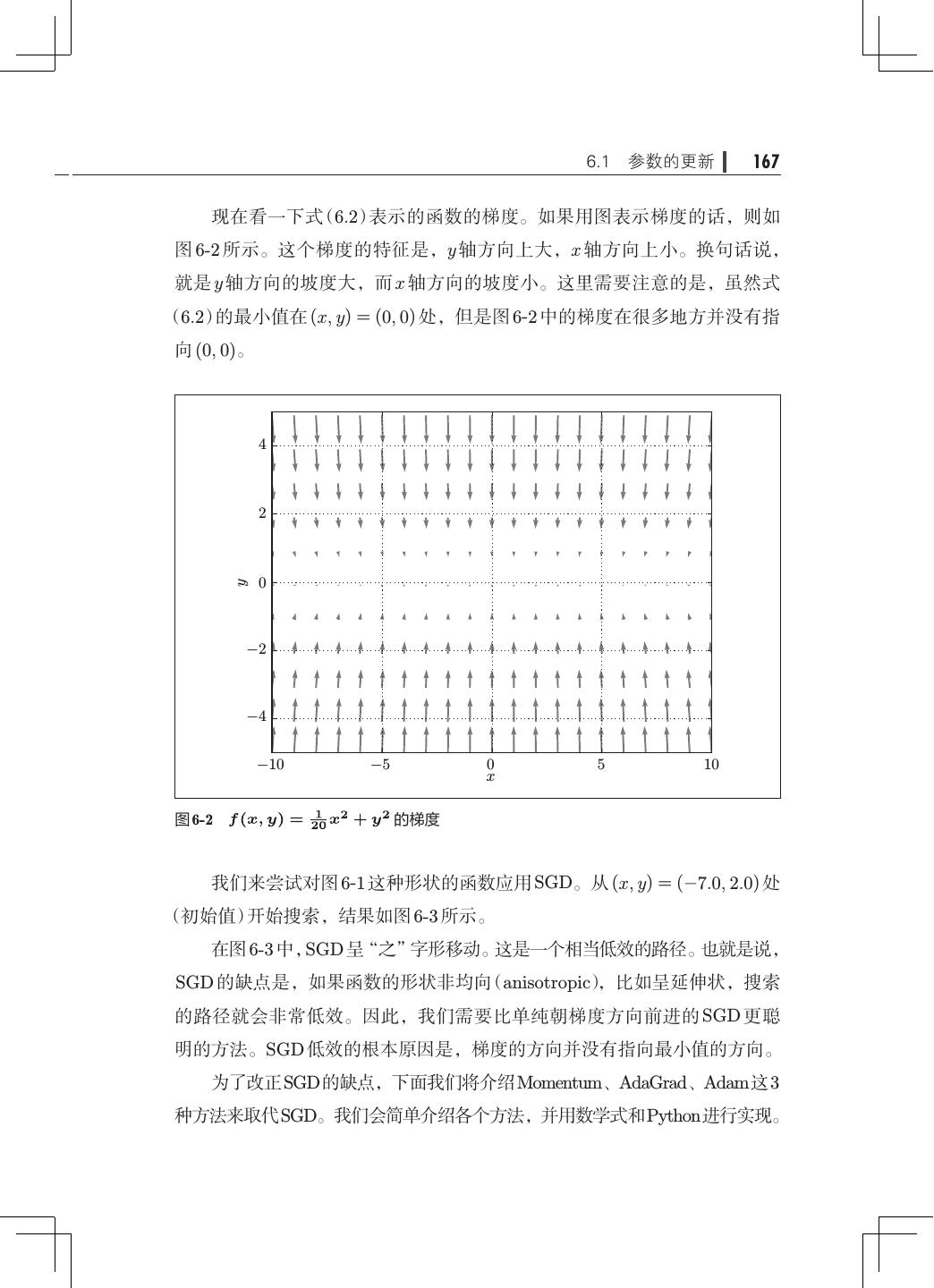
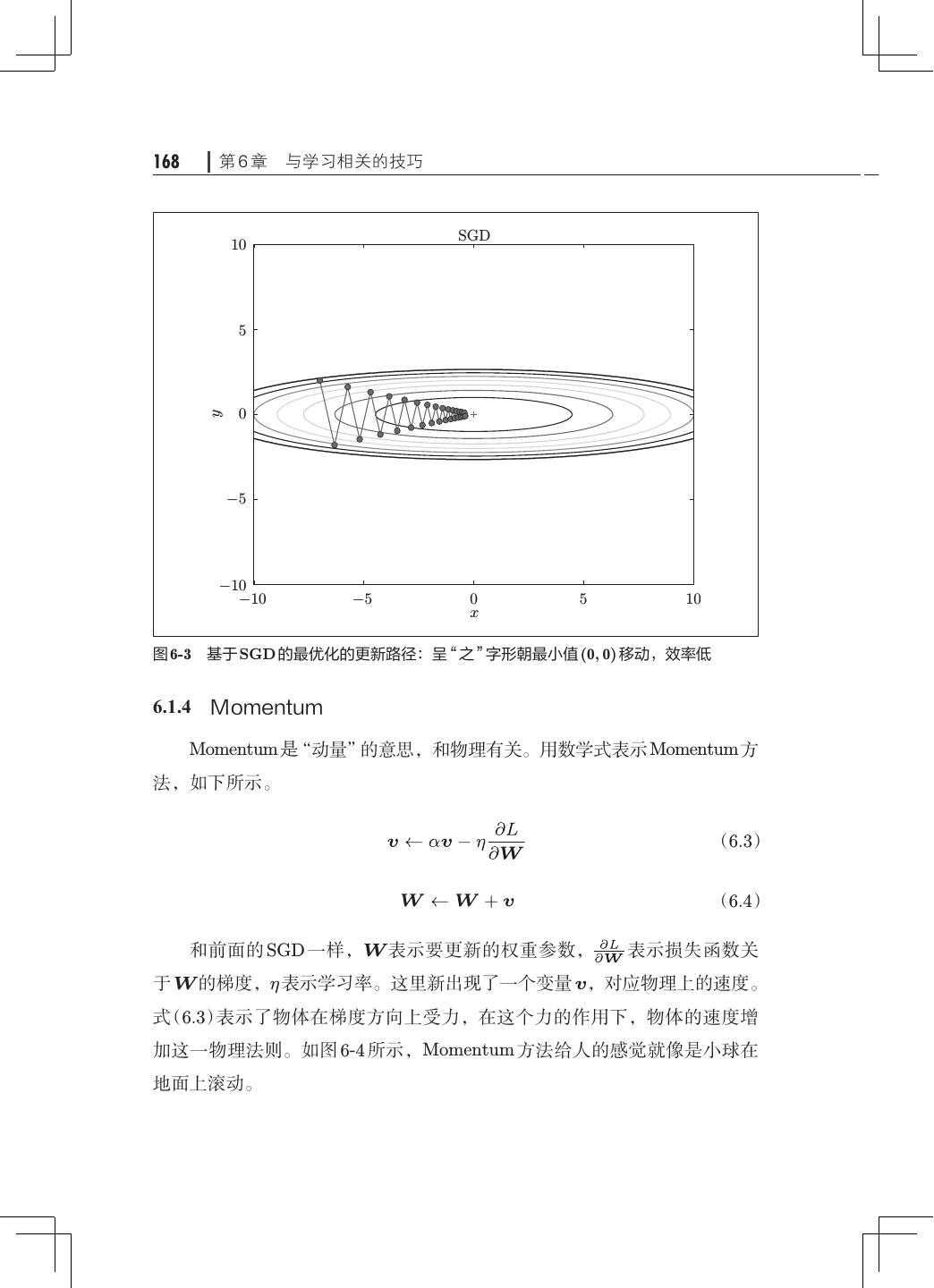
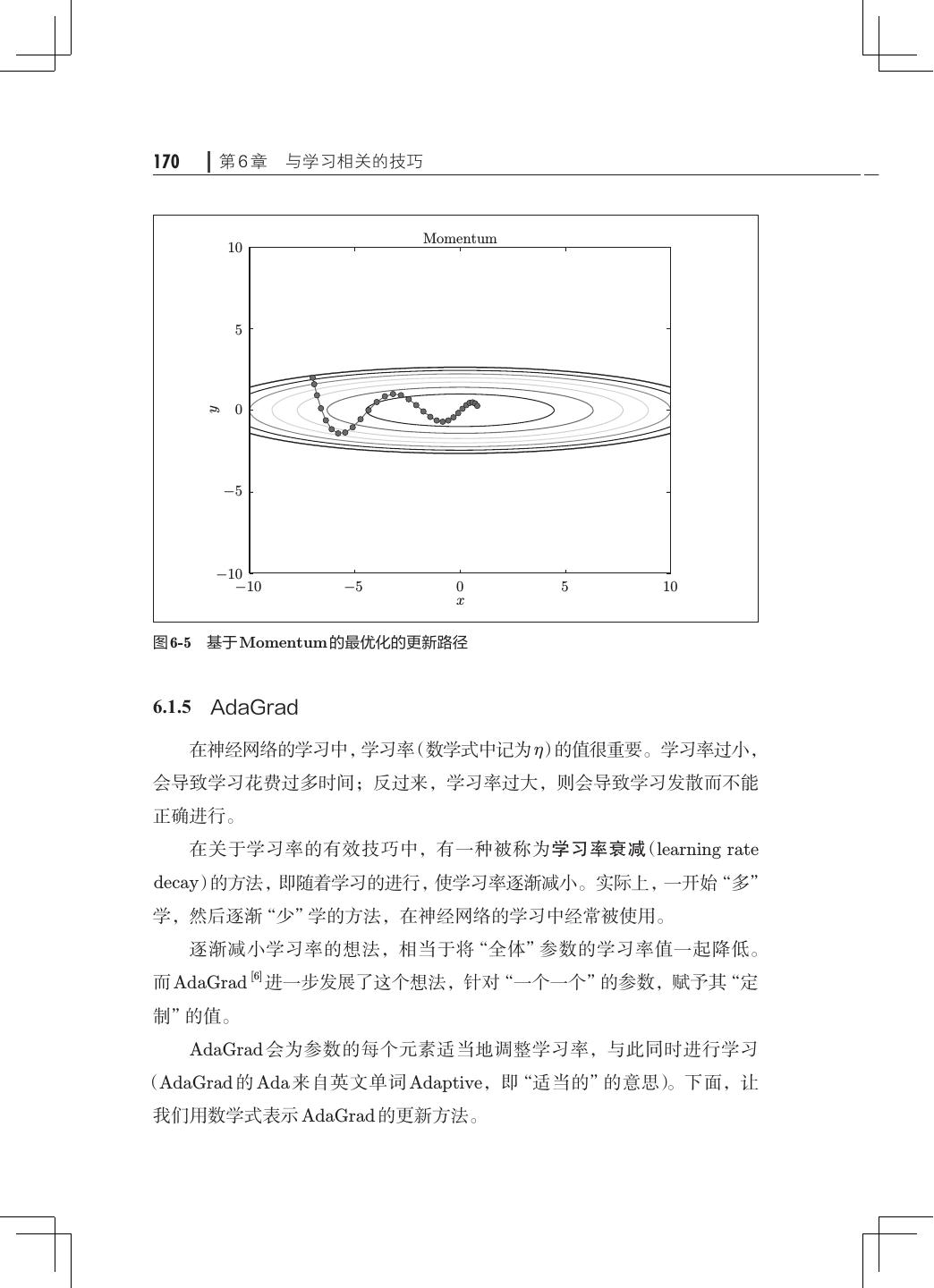
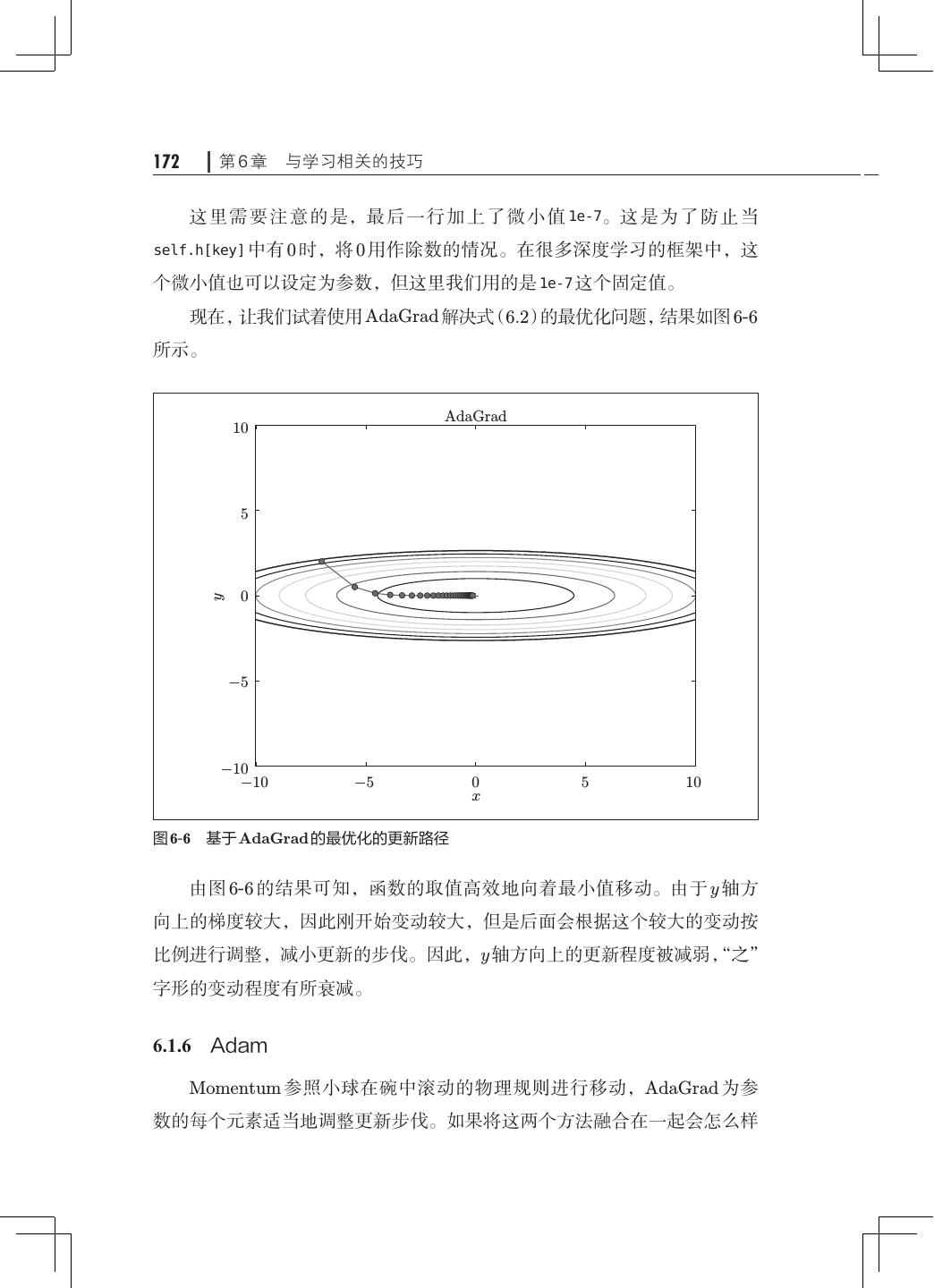
13 .x 目录 第 6 章 与学习相关的技巧· ·····································163 6.1 参数的更新· ···········································163 6.1.1 探险家的故事· ···································164 6.1.2 SGD· ·········································· 164 6.1.3 SGD 的缺点· ···································· 166 6.1.4 Momentum······································168 6.1.5 AdaGrad········································170 6.1.6 Adam· ·········································172 6.1.7 使用哪种更新方法呢· ·····························174 6.1.8 基于 MNIST 数据集的更新方法的比较· ···············175 6.2 权重的初始值· ·········································176 6.2.1 可以将权重初始值设为 0 吗· ························176 6.2.2 隐藏层的激活值的分布· ··························· 177 6.2.3 ReLU 的权重初始值 ·······························181 6.2.4 基于 MNIST 数据集的权重初始值的比较 183 · ············· 6.3 Batch Normalization· ···································184 6.3.1 Batch Normalization 的算法· ·······················184 6.3.2 Batch Normalization 的评估· ·······················186 6.4 正则化················································188 6.4.1 过拟合··········································189 6.4.2 权值衰减········································191 6.4.3 Dropout· ·······································192 6.5 超参数的验证· ·········································195 6.5.1 验证数据········································195 6.5.2 超参数的最优化· ·································196 6.5.3 超参数最优化的实现· ·····························198 6.6 小结··················································200
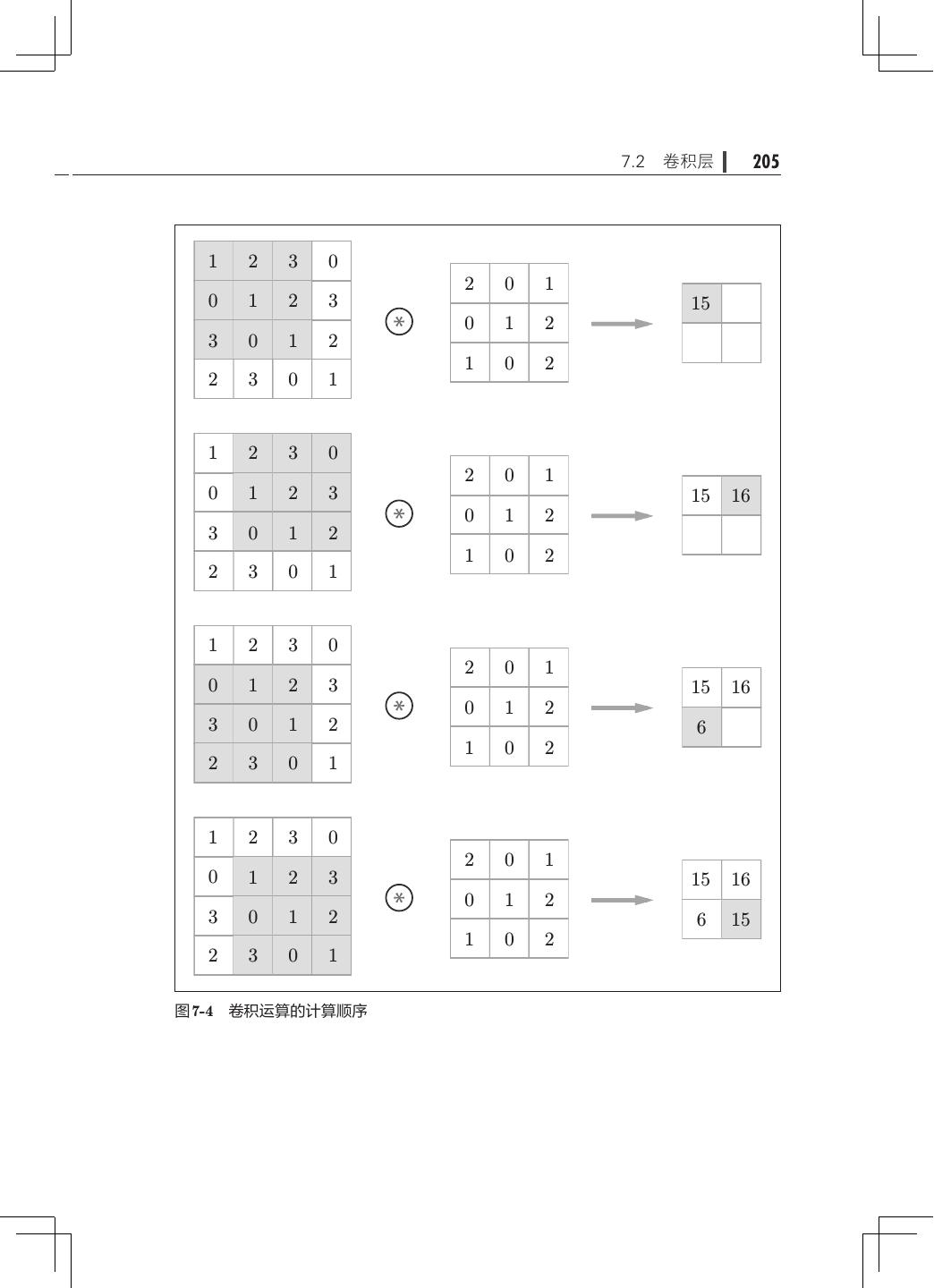
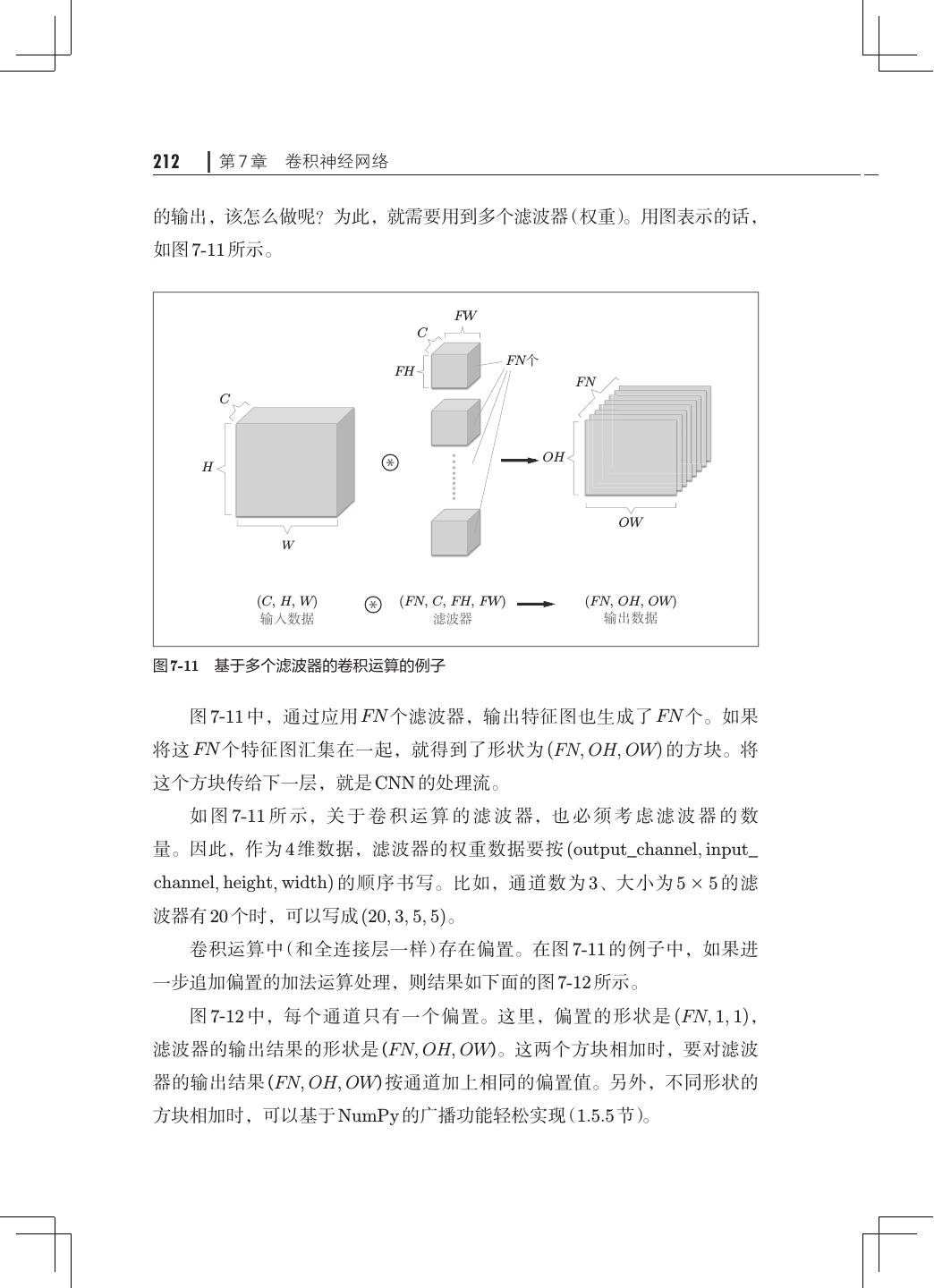
14 . 目录 xi 第 7 章 卷积神经网络· ·········································201 7.1 整体结构··············································201 7.2 卷积层················································202 7.2.1 全连接层存在的问题· ·····························203 7.2.2 卷积运算········································203 7.2.3 填充············································206 7.2.4 步幅············································207 7.2.5 3 维数据的卷积运算· ······························209 7.2.6 结合方块思考· ···································211 7.2.7 批处理··········································213 7.3 池化层················································214 7.4 卷积层和池化层的实现· ································· 216 7.4.1 4 维数组· ·······································216 7.4.2 基于 im2col 的展开 217 · ······························· 7.4.3 卷积层的实现 219 · ··································· 7.4.4 池化层的实现· ···································222 7.5 CNN 的实现· ··········································224 7.6 CNN 的可视化· ········································228 7.6.1 第 1 层权重的可视化·······························228 7.6.2 基于分层结构的信息提取· ························· 230 7.7 具有代表性的 CNN ····································· 231 7.7.1 LeNet· ·········································231 7.7.2 AlexNet·········································232 7.8 小结··················································233 第 8 章 深度学习··············································235 8.1 加深网络··············································235 8.1.1 向更深的网络出发· ·······························235 8.1.2 进一步提高识别精度· ·····························238
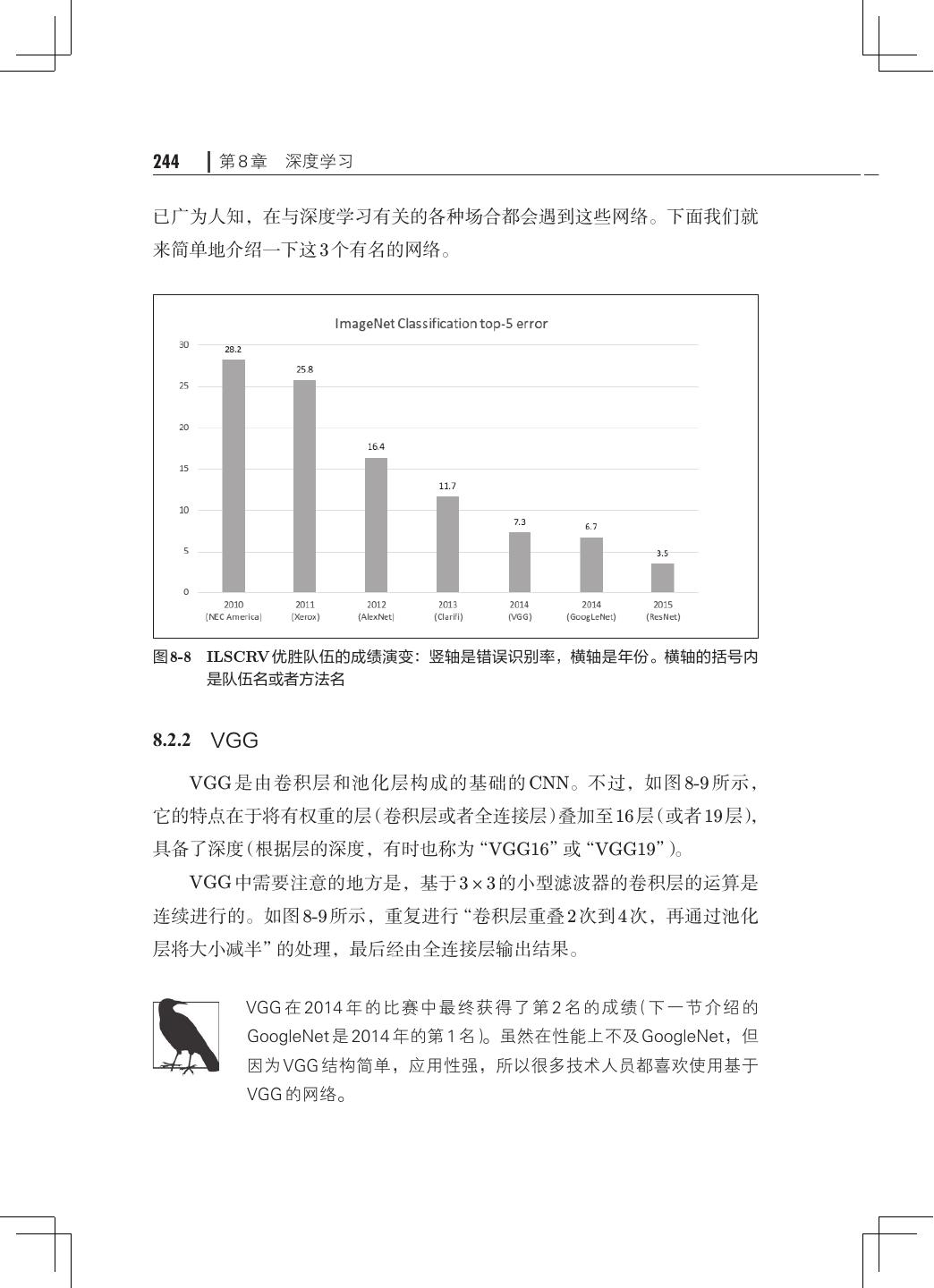
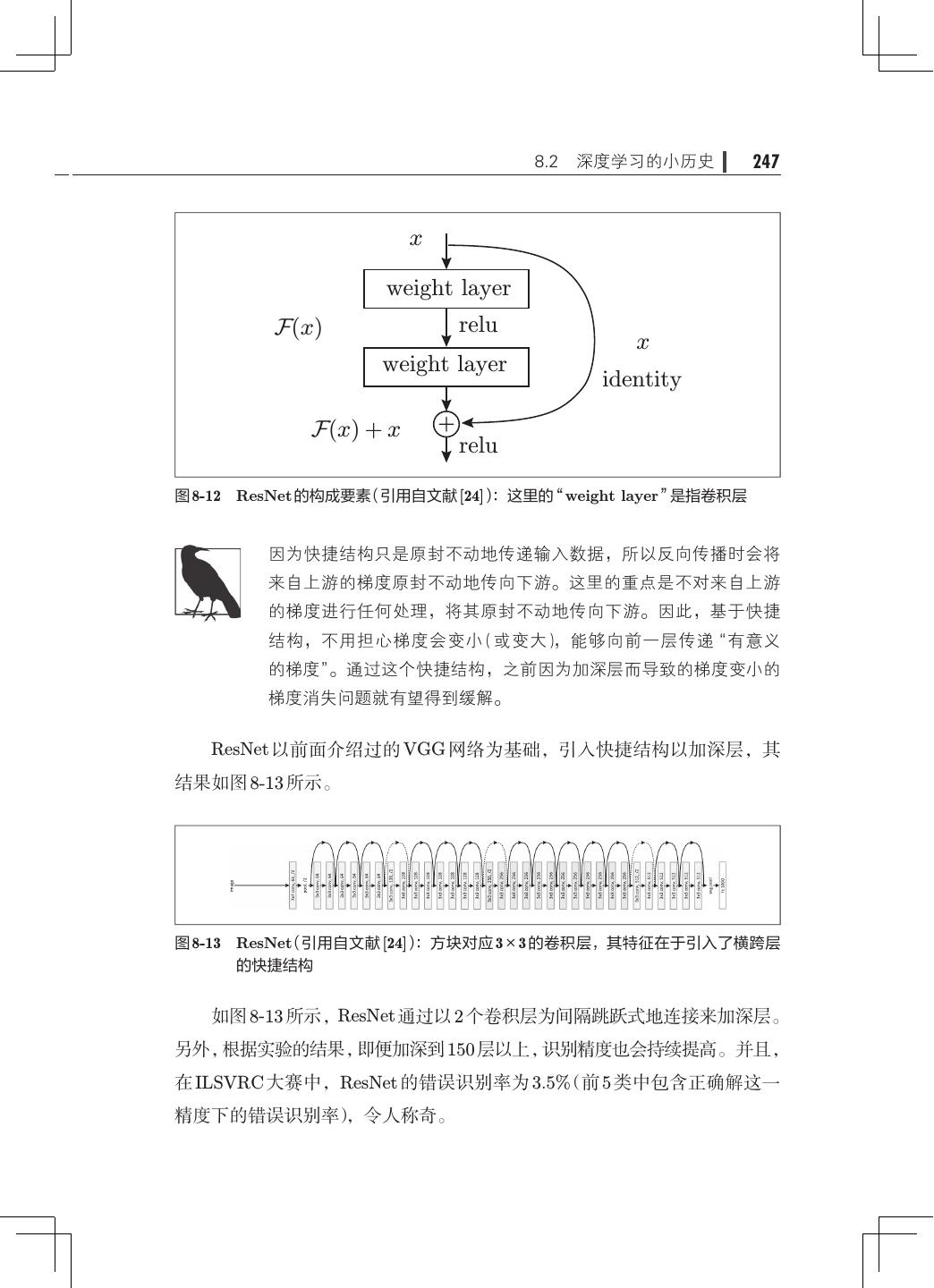
15 .xii 目录 8.1.3 加深层的动机· ···································240 8.2 深度学习的小历史· ·····································242 8.2.1 ImageNet· ······································243 8.2.2 VGG· ··········································244 8.2.3 GoogLeNet· ·····································245 8.2.4 ResNet· 246 ········································ 8.3 深度学习的高速化· ·····································248 8.3.1 需要努力解决的问题· ·····························248 8.3.2 基于 GPU 的高速化· ······························249 8.3.3 分布式学习······································250 8.3.4 运算精度的位数缩减· ·····························252 8.4 深度学习的应用案例· ···································253 8.4.1 物体检测········································253 8.4.2 图像分割········································255 8.4.3 图像标题的生成· ·································256 8.5 深度学习的未来· ·······································258 8.5.1 图像风格变换· ···································258 8.5.2 图像的生成······································259 8.5.3 自动驾驶········································261 8.5.4 Deep Q-Network(强化学习)· ·······················262 8.6 小结··················································264 附录 A Softmax-with-Loss 层的计算图· ···························267 A.1 正向传播· ············································268 A.2 反向传播· ············································270 A.3 小结· ················································277 参考文献· ····················································279
16 . 译者序 深度学习的浪潮已经汹涌澎湃了一段时间了,市面上相关的图书也已经 出版了很多。其中,既有知名学者伊恩·古德费洛(Ian Goodfellow)等人撰 写的系统介绍深度学习基本理论的《深度学习》,也有各种介绍深度学习框 架的使用方法的入门书。你可能会问,现在再出一本关于深度学习的书,是 不是“为时已晚” ?其实并非如此,因为本书考察深度学习的角度非常独特, 它的出版可以说是“千呼万唤始出来”。 本书最大的特点是“剖解”了深度学习的底层技术。正如美国物理学家 理 查 德·费 曼(Richard Phillips Feynman)所 说: “What I cannot create, I do not understand.”只有创造一个东西,才算真正弄懂了一个问题。本书就 是教你如何创建深度学习模型的一本书。并且,本书不使用任何现有的深度 学习框架,尽可能仅使用最基本的数学知识和 Python 库,从零讲解深度学 习核心问题的数学原理,从零创建一个经典的深度学习网络。 本书的日文版曾一度占据了东京大学校内书店(本乡校区)理工类图书 的畅销书榜首。各类读者阅读本书,均可有所受益。对于非 AI 方向的技术 人员,本书将大大降低入门深度学习的门槛;对于在校的大学生、研究生, 本书不失为学习深度学习的一本好教材;即便是对于在工作中已经熟练使用 框架开发各类深度学习模型的读者,也可以从本书中获得新的体会。 本书从开始翻译到出版,前前后后历时一年之久。译者翻译时力求忠于 原文,表达简练。为了保证翻译质量,每翻译完一章后,译者都会放置一段
17 .xiv 译者序 时间,再重新检查一遍。图灵公司的专业编辑们又进一步对译稿进行了全面 细致的校对,提出了许多宝贵意见,在此表示感谢。但是,由于译者才疏学浅, 书中难免存在一些错误或疏漏,恳请读者批评指正,以便我们在重印时改正。 最后,希望本书的出版能为国内的 AI 技术社区添砖加瓦! 陆宇杰 2018 年 2 月 上海
18 . 前言 科幻电影般的世界已经变成了现实—人工智能战胜过日本将棋、国际 象棋的冠军,最近甚至又打败了围棋冠军;智能手机不仅可以理解人们说的话, 还能在视频通话中进行实时的“机器翻译”;配备了摄像头的“自动防撞的车” 保护着人们的生命安全,自动驾驶技术的实用化也为期不远。环顾我们的四 周,原来被认为只有人类才能做到的事情,现在人工智能都能毫无差错地完 成,甚至试图超越人类。因为人工智能的发展,我们所处的世界正在逐渐变 成一个崭新的世界。 在这个发展速度惊人的世界背后,深度学习技术在发挥着重要作用。对 于深度学习,世界各地的研究人员不吝褒奖之辞,称赞其为革新性技术,甚 至有人认为它是几十年才有一次的突破。实际上,深度学习这个词经常出现 在报纸和杂志中,备受关注,就连一般大众也都有所耳闻。 本书就是一本以深度学习为主题的书,目的是让读者尽可能深入地理解 深度学习的技术。因此,本书提出了“从零开始”这个概念。 本书的特点是通过实现深度学习的过程,来逼近深度学习的本质。通过 实现深度学习的程序,尽可能无遗漏地介绍深度学习相关的技术。另外,本 书还提供了实际可运行的程序,供读者自己进行各种各样的实验。 为了实现深度学习,我们需要经历很多考验,花费很长时间,但是相应 地也能学到和发现很多东西。而且,实现深度学习的过程是一个有趣的、令
19 .xvi 前言 人兴奋的过程。希望读者通过这一过程可以熟悉深度学习中使用的技术,并 能从中感受到快乐。 目前,深度学习活跃在世界上各个地方。在几乎人手一部的智能手机中、 开启自动驾驶的汽车中、为 Web 服务提供动力的服务器中,深度学习都在 发挥着作用。此时此刻,就在很多人没有注意到的地方,深度学习正在默默 地发挥着其功能。今后,深度学习势必将更加活跃。为了让读者理解深度学 习的相关技术,感受到深度学习的魅力,笔者写下了本书。 本书的理念 本书是一本讲解深度学习的书,将从最基础的内容开始讲起,逐一介绍 理解深度学习所需的知识。书中尽可能用平实的语言来介绍深度学习的概念、 特征、工作原理等内容。不过,本书并不是只介绍技术的概要,而是旨在让 读者更深入地理解深度学习。这是本书的特色之一。 那么,怎么才能更深入地理解深度学习呢?在笔者看来,最好的办法就 是亲自实现。从零开始编写可实际运行的程序,一边看源代码,一边思考。 笔者坚信,这种做法对正确理解深度学习(以及那些看上去很高级的技术) 是很重要的。这里用了“从零开始”一词,表示我们将尽可能地不依赖外部 的现成品(库、工具等)。也就是说,本书的目标是,尽量不使用内容不明的 黑盒,而是从自己能理解的最基础的知识出发,一步一步地实现最先进的深 度学习技术。并通过这一实现过程,使读者加深对深度学习的理解。 如果把本书比作一本关于汽车的书,那么本书并不会教你怎么开车,其 着眼点不是汽车的驾驶方法,而是要让读者理解汽车的原理。为了让读者理 解汽车的结构,必须打开汽车的引擎盖,把零件一个一个地拿在手里观察, 并尝试操作它们。之后,用尽可能简单的形式提取汽车的本质,并组装汽车 模型。本书的目标是,通过制造汽车模型的过程,让读者感受到自己可以实 际制造出汽车,并在这一过程中熟悉汽车相关的技术。 为了实现深度学习,本书使用了 Python 这一编程语言。Python 非常受 欢迎,初学者也能轻松使用。Python 尤其适合用来制作样品(原型),使用
20 . 前言 xvii Python 可以立刻尝试突然想到的东西,一边观察结果,一边进行各种各样 的实验。本书将在讲解深度学习理论的同时,使用 Python 实现程序,进行 各种实验。 在光看数学式和理论说明无法理解的情况下,可以尝试阅读源代码 并运行,很多时候思路都会变得清晰起来。对数学式感到困惑时, 就阅读源代码来理解技术的流程,这样的事情相信很多人都经历过。 本书通过实际实现(落实到代码)来理解深度学习,是一本强调“工程” 的书。书中会出现很多数学式,但同时也会有很多程序员视角的源代码。 本书面向的读者 本书旨在让读者通过实际动手操作来深入理解深度学习。为了明确本书 的读者对象,这里将本书涉及的内容列举如下。 • 使用 Python,尽可能少地使用外部库,从零开始实现深度学习的程序。 • 为了让 Python 的初学者也能理解,介绍 Python 的使用方法。 • 提供实际可运行的 Python 源代码,同时提供可以让读者亲自实验的 学习环境。 • 从简单的机器学习问题开始,最终实现一个能高精度地识别图像的系统。 • 以简明易懂的方式讲解深度学习和神经网络的理论。 • 对于误差反向传播法、卷积运算等乍一看很复杂的技术,使读者能够 在实现层面上理解。 • 介绍一些学习深度学习时有用的实践技巧,如确定学习率的方法、权 重的初始值等。 • 介绍最近流行的 Batch Normalization、Dropout、Adam 等,并进行 实现。 • 讨论为什么深度学习表现优异、为什么加深层能提高识别精度、为什 么隐藏层很重要等问题。 • 介绍自动驾驶、图像生成、强化学习等深度学习的应用案例。
21 .xviii 前言 本书不面向的读者 明确本书不适合什么样的读者也很重要。为此,这里将本书不会涉及的 内容列举如下。 • 不介绍深度学习相关的最新研究进展。 • 不介绍 Caffe、TensorFlow、Chainer 等深度学习框架的使用方法。 • 不介绍深度学习的详细理论,特别是神经网络相关的详细理论。 • 不详细介绍用于提高识别精度的参数调优相关的内容。 • 不会为了实现深度学习的高速化而进行 GPU 相关的实现。 • 本书以图像识别为主题,不涉及自然语言处理或者语音识别的例子。 综上,本书不涉及最新研究和理论细节。但是,读完本书之后,读者 应该有能力进一步去阅读最新的论文或者神经网络相关的理论方面的技 术书。 本书以图像识别为主题,主要学习使用深度学习进行图像识别时 所需的技术。自然语言处理或者语音识别等不是本书的讨论对象。 本书的阅读方法 学习新知识时,只听别人讲解的话,有时会无法理解,或者会立刻忘记。 正如“不闻不若闻之,闻之不若见之,见之不若知之,知之不若行之”A ,在 学习新东西时,没有什么比实践更重要了。本书在介绍某个主题时,都细心 地准备了一个可以实践的场所——能够作为程序运行的源代码。 本书会提供 Python 源代码,读者可以自己动手实际运行这些源代码。 在阅读源代码的同时,可以尝试去实现一些自己想到的东西,以确保真正 A 出自荀子《儒效篇》。
22 . 前言 xix 理解了。另外,读者也可以使用本书的源代码,尝试进行各种实验,反复 试错。 本书将沿着“理论说明”和“Python 实现”两个路线前进。因此,建议 读者准备好编程环境。本书可以使用 Windows、Mac、Linux 中的任何一个 系统。关于 Python 的安装和使用方法将在第 1 章介绍。另外,本书中用到 的程序可以从以下网址下载。 http://www.ituring.com.cn/book/1921 让我们开始吧 通过前面的介绍,希望读者了解本书大概要讲的内容,产生继续阅读的 兴趣。 最近出现了很多深度学习相关的库,任何人都可以方便地使用。实际上, 使用这些库的话,可以轻松地运行深度学习的程序。那么,为什么我们还要 特意花时间从零开始实现深度学习呢?一个理由就是,在制作东西的过程中 可以学到很多。 在制作东西的过程中,会进行各种各样的实验,有时也会卡住,抱着脑 袋想为什么会这样。这种费时的工作对深刻理解技术而言是宝贵的财富。像 这样认真花费时间获得的知识在使用现有的库、阅读最新的文章、创建原创 的系统时都大有用处。而且最重要的是,制作本身就是一件快乐的事情。(还 需要快乐以外的其他什么理由吗?) 既然一切都准备好了,下面就让我们踏上实现深度学习的旅途吧! 表述规则 本书在表述上采用如下规则。 粗体字(Bold) 用来表示新引入的术语、强调的要点以及关键短语。
23 .xx 前言 等宽字(Constant Width) 用来表示下面这些信息:程序代码、命令、序列、组成元素、语句选项、 分支、变量、属性、键值、函数、类型、类、命名空间、方法、模块、属性、 参数、值、对象、事件、事件处理器、XML 标签、HTML 标签、宏、文件 的内容、来自命令行的输出等。若在其他地方引用了以上这些内容(如变量、 函数、关键字等),也会使用该格式标记。 等宽粗体字(Constant Width Bold) 用来表示用户输入的命令或文本信息。在强调代码的作用时也会使用该 格式标记。 等宽斜体字(Constant Width Italic) 用来表示必须根据用户环境替换的字符串。 用来表示提示、启发以及某些值得深究的内容的补充信息。 表示程序库中存在的 bug 或时常会发生的问题等警告信息,引 起读者对该处内容的注意。 读者意见与咨询 虽然笔者已经尽最大努力对本书的内容进行了验证与确认,但仍不免在 某些地方出现错误或者容易引起误解的表达等,给读者的理解带来困扰。如 果读者遇到这些问题,请及时告知,我们在本书重印时会将其改正,在此先 表示不胜感激。与此同时,也希望读者能够为本书将来的修订提出中肯的建 议。本书编辑部的联系方式如下。
24 . 前言 xxi 株式会社 O’ Reilly Japan 电子邮件 japan@oreilly.co.jp 本书的主页地址如下。 http://www.ituring.com.cn/book/1583 http://www.oreilly.co.jp/books/9784873117584(日语) https://github.com/oreilly-japan/deep-learning-from-scratch 关于 O’ Reilly 的其他信息,可以访问下面的 O’ Reilly 主页查看。 http://www.oreilly.com/(英语) http://www.oreilly.co.jp/(日语) 致谢 首先,笔者要感谢推动了深度学习相关技术(机器学习、计算机科学等) 发展的研究人员和工程师。本书的完成离不开他们的研究工作。其次,笔者 还要感谢在图书或网站上公开有用信息的各位同仁。其中,斯坦福大学的 CS231n [5] 公开课慷慨提供了很多有用的技术和信息,笔者从中学到了很多东西。 在本书执笔过程中,曾受到下列人士的帮助:teamLab 公司的加藤哲朗、 喜多慎弥、飞永由夏、中野皓太、中村将达、林辉大、山本辽;Top Studio 公司的武藤健志、增子萌;Flickfit 公司的野村宪司;得克萨斯大学奥斯汀 分校 JSPS 海外特别研究员丹野秀崇。他们阅读了本书原稿,提出了很多宝 贵的建议,在此深表谢意。另外,需要说明的是,本书中存在的不足或错误 均是笔者的责任。 最后,还要感谢 O’ Reilly Japan 的宮川直树,在从本书的构想到完成的 大约一年半的时间里,宫川先生一直支持着笔者。非常感谢! 2016 年 9 月 1 日 斋藤康毅
25 .
26 . 第1章 Python 入门 Python 这一编程语言已经问世 20 多年了,在这期间,Python 不仅完成 了自身的进化,还获得了大量的用户。现在,Python 作为最具人气的编程语言, 受到了许多人的喜爱。 接下来我们将使用 Python 实现深度学习系统。不过在这之前,本章将简 单地介绍一下 Python,看一下它的使用方法。已经掌握了 Python、NumPy、 Matplotlib 等知识的读者,可以跳过本章,直接阅读后面的章节。 1.1 Python 是什么 Python 是一个简单、易读、易记的编程语言,而且是开源的,可以免 费地自由使用。Python 可以用类似英语的语法编写程序,编译起来也不费 力,因此我们可以很轻松地使用 Python。特别是对首次接触编程的人士来说, Python 是最合适不过的语言。事实上,很多高校和大专院校的计算机课程 均采用 Python 作为入门语言。 此外,使用 Python 不仅可以写出可读性高的代码,还可以写出性能高(处 理速度快)的代码。在需要处理大规模数据或者要求快速响应的情况下,使 用 Python 可以稳妥地完成。因此,Python 不仅受到初学者的喜爱,同时也 受到专业人士的喜爱。实际上,Google、Microsoft、Facebook 等战斗在 IT 行业最前沿的企业也经常使用 Python。
27 .2 第 1 章 Python 入门 再者,在科学领域,特别是在机器学习、数据科学领域,Python 也被 大 量 使 用。Python 除 了 高 性 能 之 外,凭 借 着 NumPy、SciPy 等 优 秀 的 数 值计算、统计分析库,在数据科学领域占有不可动摇的地位。深度学习的 框架中也有很多使用 Python 的场景,比如 Caffe、TensorFlow、Chainer、 Theano 等著名的深度学习框架都提供了 Python 接口。因此,学习 Python 对使用深度学习框架大有益处。 综上,Python 是最适合数据科学领域的编程语言。而且,Python 具有 受众广的优秀品质,从初学者到专业人士都在使用。因此,为了完成本书的 从零开始实现深度学习的目标,Python 可以说是最合适的工具。 1.2 Python 的安装 下面,我们首先将 Python 安装到当前环境(电脑)上。这里说明一下安 装时需要注意的一些地方。 1.2.1 Python 版本 Python 有 Python 2.x 和 Python 3.x 两个版本。如果我们调查一下目前 Python 的使用情况,会发现除了最新的版本 3.x 以外,旧的版本 2.x 仍在被 大量使用。因此,在安装 Python 时,需要慎重选择安装 Python 的哪个版 本。这是因为两个版本之间没有兼容性(严格地讲,是没有“向后兼容性”), 也就是说,会发生用 Python 3.x 写的代码不能被 Python 2.x 执行的情况。 本 书 中 使 用 Python 3.x,只 安 装 了 Python 2.x 的 读 者 建 议 另 外 安 装 一 下 Python 3.x。 1.2.2 使用的外部库 本书的目标是从零开始实现深度学习。因此,除了NumPy库和Matplotlib 库之外,我们极力避免使用外部库。之所以使用这两个库,是因为它们可以 有效地促进深度学习的实现。
28 . 1.2 Python 的安装 3 NumPy 是用于数值计算的库,提供了很多高级的数学算法和便利的数 组(矩阵)操作方法。本书中将使用这些便利的方法来有效地促进深度学习 的实现。 Matplotlib 是用来画图的库。使用 Matplotlib 能将实验结果可视化,并 在视觉上确认深度学习运行期间的数据。 本书将使用下列编程语言和库。 • Python 3.x(2016 年 8 月时的最新版本是 3.5) • NumPy • Matplotlib 下面将为需要安装 Python 的读者介绍一下 Python 的安装方法。已经安 装了 Python 的读者,请跳过这一部分内容。 1.2.3 Anaconda 发行版 Python 的安装方法有很多种,本书推荐使用 Anaconda 这个发行版。发 行版集成了必要的库,使用户可以一次性完成安装。Anaconda 是一个侧重 于数据分析的发行版,前面说的 NumPy、Matplotlib 等有助于数据分析的 库都包含在其中 A。 如前所述,本书将使用 Python 3.x 版本,因此 Anaconda 发行版也要安 装 3.x 的版本。请读者从官方网站下载与自己的操作系统相应的发行版,然 后安装。 A Anaconda 作为一个针对数据分析的发行版,包含了许多有用的库,而本书中实际上只会使用其中的 NumPy 库和 Matplotlib 库。因此,如果想保持轻量级的开发环境,单独安装这两个库也是可以的。 ——译者注
29 .4 第 1 章 Python 入门 1.3 Python 解释器 完成 Python 的安装后,要先确认一下 Python的版本。打开终端(Windows 中的命令行窗口),输入 python --version 命令,该命令会输出已经安装的 Python 的版本信息。 $ python --version Python 3.4.1 :: Anaconda 2.1.0 (x86_64) 如上所示,显示了 Python 3.4.1(根据实际安装的版本,版本号可能不同), 说明已正确安装了 Python 3.x。接着输入 python,启动 Python 解释器。 $ python Python 3.4.1 |Anaconda 2.1.0 (x86_64)| (default, Sep 10 2014, 17:24:09) [GCC 4.2.1 (Apple Inc. build 5577)] on darwin Type "help", "copyright", "credits" or "license" for more information. >>> Python 解释器也被称为“对话模式”,用户能够以和 Python 对话的方式 进行编程。比如,当用户询问“1 + 2 等于几?”的时候,Python 解释器会回 答“3”,所谓对话模式,就是指这样的交互。现在,我们实际输入一下看看。 >>> 1 + 2 3 Python 解释器可以像这样进行对话式(交互式)的编程。下面,我们使 用这个对话模式,来看几个简单的 Python 编程的例子。 1.3.1 算术计算 加法或乘法等算术计算,可按如下方式进行。 >>> 1 - 2 -1 >>> 4 * 5 20