神经-符号系统的一些探索

1 . http://lamda.nju.edu.cn 神经-符号系统的⼀些探索 俞扬 joint work with: 周志华教授、戴望州、徐秋灵、胡扬阳 南京大学 软件新技术国家重点实验室 机器学习与数据挖掘研究所（LAMDA） 

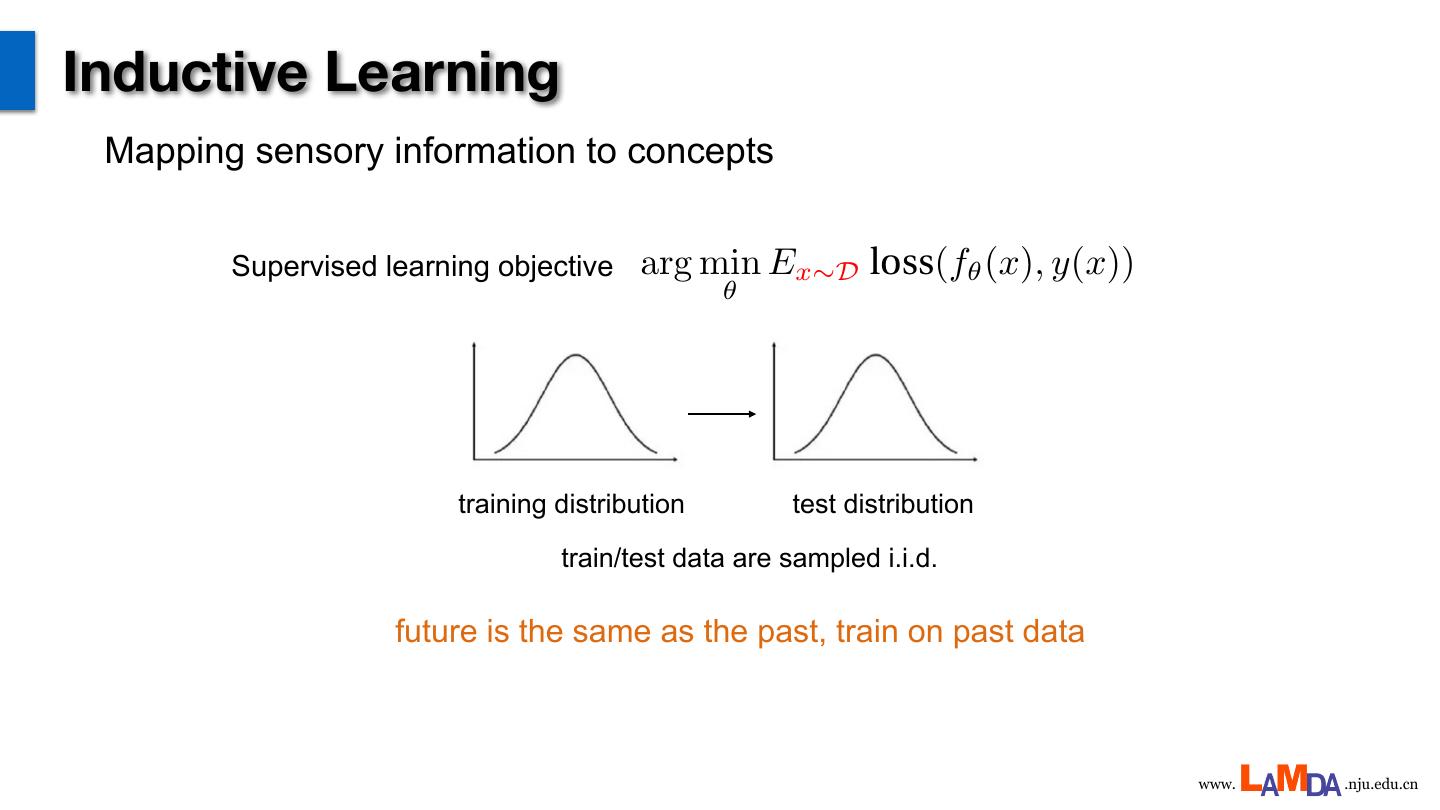
2 .Inductive Learning Mapping sensory information to concepts Supervised learning objective arg min Ex⇠D loss(f✓ (x), y(x)) <latexit sha1_base64="1xDDF2NgKSjn1X59ZKKFTSSDkb4=">AAADbHicZVJNbxMxEHUTPsrylQK3CskiAiVSG+2GIq6toBLcWom0ldarldeZbFax1yvboYks/y5+CweucOM34GxDYZORbI3fvPdmLE1W8UKbMPy+02rfuXvv/u6D4OGjx0+edvaeXWg5VwxGTHKprjKqgRcljExhOFxVCqjIOFxmsw+r+uVXULqQ5RezrCARNC+LScGo8VDaOSdU5UQUZUrMFAzFp6klta1VMHYLoguBiaBmyijHHx3BxMDCWC61dr2JJ9cy11v0D/DS3/200w0HYR14O4nWSRet4yzda7XJWLK5gNIwTrWOo7AyiaXKFIyDC8hcQ0XZjOYQ+7SkAnRi6yEdfu2RMZ5I5U9pcI02FNV44idObK5oNS3YounHBCyi0DcTevXJRtHOjawK2sQ8US9FtgWuuusmujI0UnK9RTZT0cSyjTfluVSFp20O/K/igoDcdtBgrJ7Ka1nypYKJPlg9BC3nlBua6xW3hGsmhcfGlsCiAmZcPEzixAbYh629ssyeutR2IxeTGajyMBxE70DEuDvEyS1yBCJxtco1bdlf3yj5z6+HuxHub1BP3A1joujMnjgX+LWJNpdkO7kYDqK3g+H5Uff483qBdtE+eoV6KELv0TH6hM7QCDH0Df1AP9Gv1u/2i/Z+++UNtbWz1jxHjWi/+QNm5B5y</latexit> ✓ training distribution test distribution train/test data are sampled i.i.d. future is the same as the past, train on past data www. .nju.edu.cn 

3 .Deep Learning Deep models (neural networks/forests) arg min Ex⇠D loss(f✓ (x), y(x)) <latexit sha1_base64="1xDDF2NgKSjn1X59ZKKFTSSDkb4=">AAADbHicZVJNbxMxEHUTPsrylQK3CskiAiVSG+2GIq6toBLcWom0ldarldeZbFax1yvboYks/y5+CweucOM34GxDYZORbI3fvPdmLE1W8UKbMPy+02rfuXvv/u6D4OGjx0+edvaeXWg5VwxGTHKprjKqgRcljExhOFxVCqjIOFxmsw+r+uVXULqQ5RezrCARNC+LScGo8VDaOSdU5UQUZUrMFAzFp6klta1VMHYLoguBiaBmyijHHx3BxMDCWC61dr2JJ9cy11v0D/DS3/200w0HYR14O4nWSRet4yzda7XJWLK5gNIwTrWOo7AyiaXKFIyDC8hcQ0XZjOYQ+7SkAnRi6yEdfu2RMZ5I5U9pcI02FNV44idObK5oNS3YounHBCyi0DcTevXJRtHOjawK2sQ8US9FtgWuuusmujI0UnK9RTZT0cSyjTfluVSFp20O/K/igoDcdtBgrJ7Ka1nypYKJPlg9BC3nlBua6xW3hGsmhcfGlsCiAmZcPEzixAbYh629ssyeutR2IxeTGajyMBxE70DEuDvEyS1yBCJxtco1bdlf3yj5z6+HuxHub1BP3A1joujMnjgX+LWJNpdkO7kYDqK3g+H5Uff483qBdtE+eoV6KELv0TH6hM7QCDH0Df1AP9Gv1u/2i/Z+++UNtbWz1jxHjWi/+QNm5B5y</latexit> ✓ Achieves extraordinary performance on sensing tasks www. .nju.edu.cn 

4 .Reinforcement learning RL using deep models arg min Es⇠D⇡✓ reward(s, ⇡✓ (s)) <latexit sha1_base64="D5znIabET++zo3gI4F6bswHDtfs=">AAADenicZVJNj9MwEPW2fCzlY7tw5GJthNSKpUpKEdddwUpwWyT2Q4pD5LjT1KodR7ZLW1n+efwIfgNXuHEg6ZaFtCNZmnnvzZuxNFkpuLFh+H2v1b5z9979/Qedh48ePznoHj69NGquGVwwJZS+zqgBwQu4sNwKuC41UJkJuMpm72r+6itow1Xx2a5KSCTNCz7hjNoKSrspoTonkhcpsVOwFJ+ljqxtnYaxN8RwiYmkdsqowO+/OFLyjdR7gomFpa2UC6rHvmeOcU27Dd8z/X7aDcJBuA68m0SbJECbOE8PW20yVmwuobBMUGPiKCxt4qi2nAnwHTI3UFI2oznEVVpQCSZx65U9flEhYzxRunqFxWu00VGOJ9XKics1LaecLZt+TMIyCqth0tRfbpBublXJaROrhGYlsx2wnm6aaG1olRJmR2ynsollWzUVudK8km0v/I/xnQ65nWDAOjNVC1WIlYaJOa4LSYs5FZbmptYWsGBKVtjYEViWwKyPh0mcuA6uwq29ssyd+dQFkY/JDHTxKhxEb0DGOBji5BYZgUz8uss3bdlf3yj5z6+Hgwj3t6Sn/kYx0XTmTr3vVGcTbR/JbnI5HESvB8NPo+Dk4+aA9tFzdIR6KEJv0Qn6gM7RBWLoG/qBfqJfrd/to3a//fJG2trb9DxDjWiP/gDrQyUU</latexit> ✓ www. .nju.edu.cn 

5 . The struggling of DL Yoshua Bengio: From System 1 Deep Learning to System 2 Deep Learning. NeurIPS’2019 Keynote deductive learning www. .nju.edu.cn 

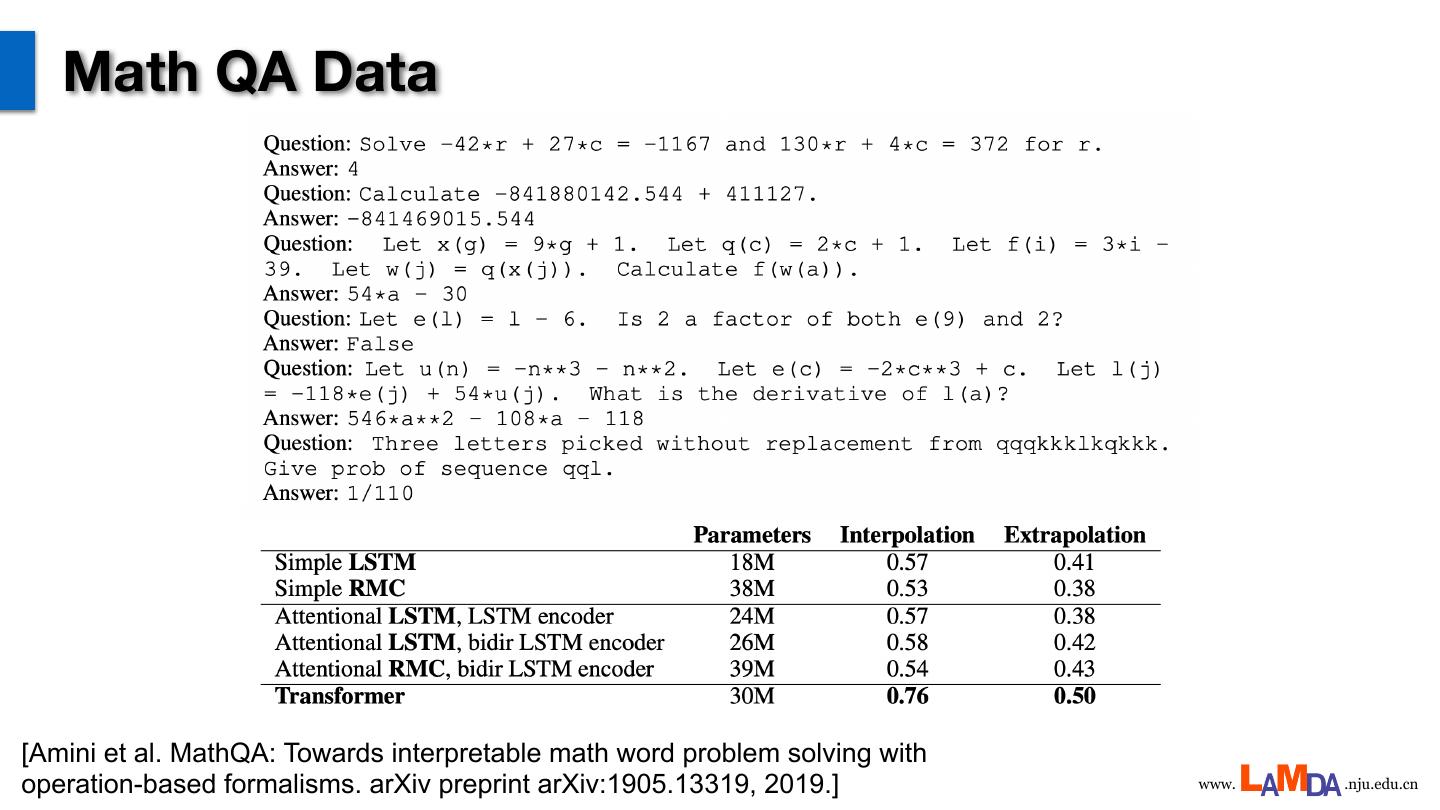
6 . Math QA Data [Amini et al. MathQA: Towards interpretable math word problem solving with operation-based formalisms. arXiv preprint arXiv:1905.13319, 2019.] www. .nju.edu.cn 

7 .Deductive learning Deductive learning is a subclass of machine learning that studies algorithms for learning provably correct knowledge. Typically such methods are used to speedup problem solvers by adding knowledge to them that is deductively entailed by existing knowledge, but that may result in faster solutions. C. Sammut, G. I. Webb. Encyclopedia of Machine Learning and Data Mining which was the beginning of AI General Problem Solving, Automated Theorem Proving, Boolean Satisfiability, Expert Systems, Logic Programming, Inductive Logic Programming, Probabilistic Logic Programming, Constraint Logic Programming, Answer Set Programming, … www. .nju.edu.cn 

8 .Inductive + Deductive ? ideally: learn concepts inductively + learn new knowledge deductively ➢ Probabilistic Logic Programming (PLP): attempts to extend first-order logic to accommodate probabilistic groundings such that probabilistic inference can be included heavy-reasoning light-learning ➢ Statistical Relational Learning (SRL): attempts to construct/initialize a probabilistic model based on domain knowledge expressed in first-order logic clauses heavy-learning light-reasoning www. .nju.edu.cn 

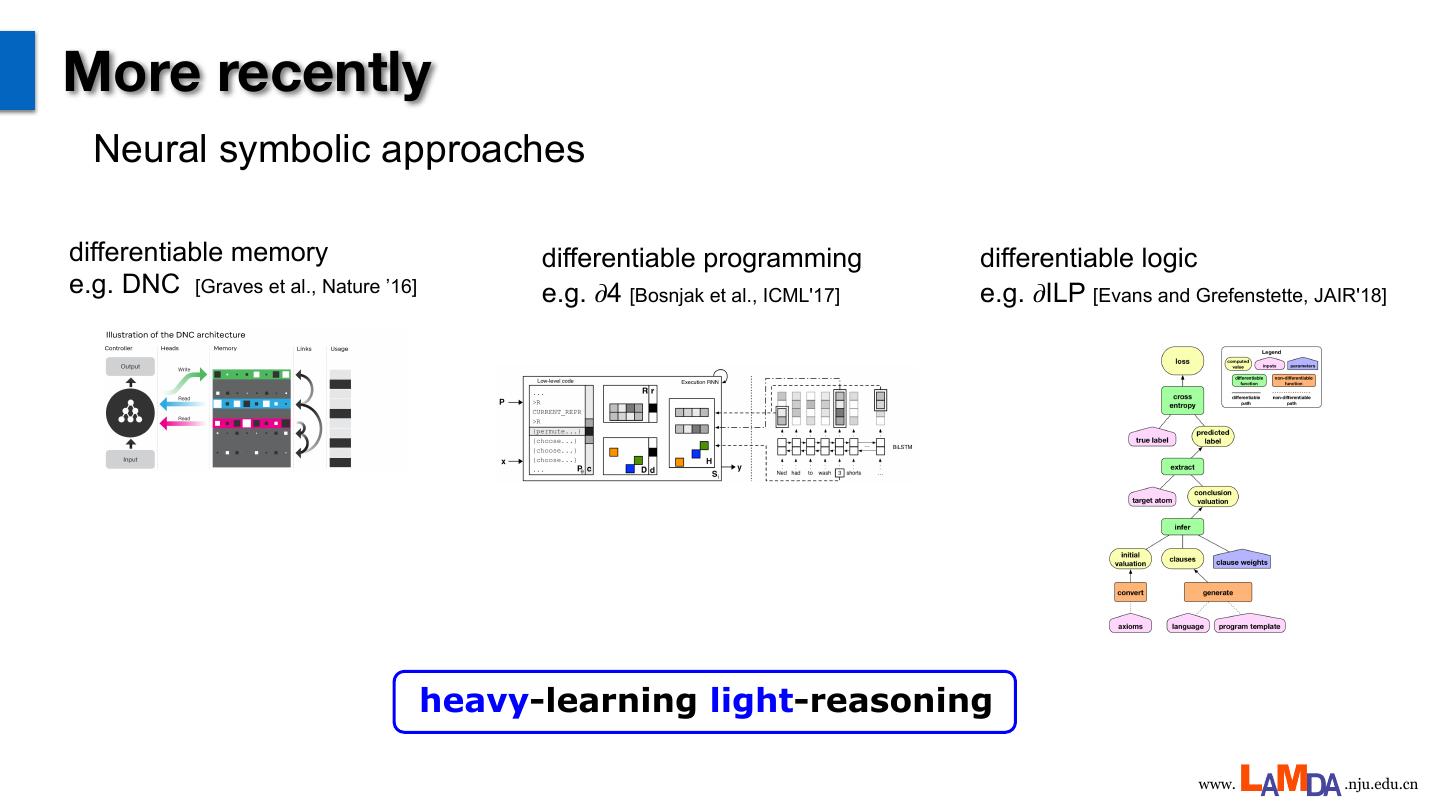
9 .More recently Neural symbolic approaches differentiable memory differentiable programming differentiable logic e.g. DNC [Graves et al., Nature ’16] e.g. 𝜕4 [Bosnjak et al., ICML'17] e.g. 𝜕ILP [Evans and Grefenstette, JAIR'18] heavy-learning light-reasoning www. .nju.edu.cn 

10 .Missing anything? Inductive + Deductive ? real values symbols differentiable non-differentiable end-to-end programmed www. .nju.edu.cn 

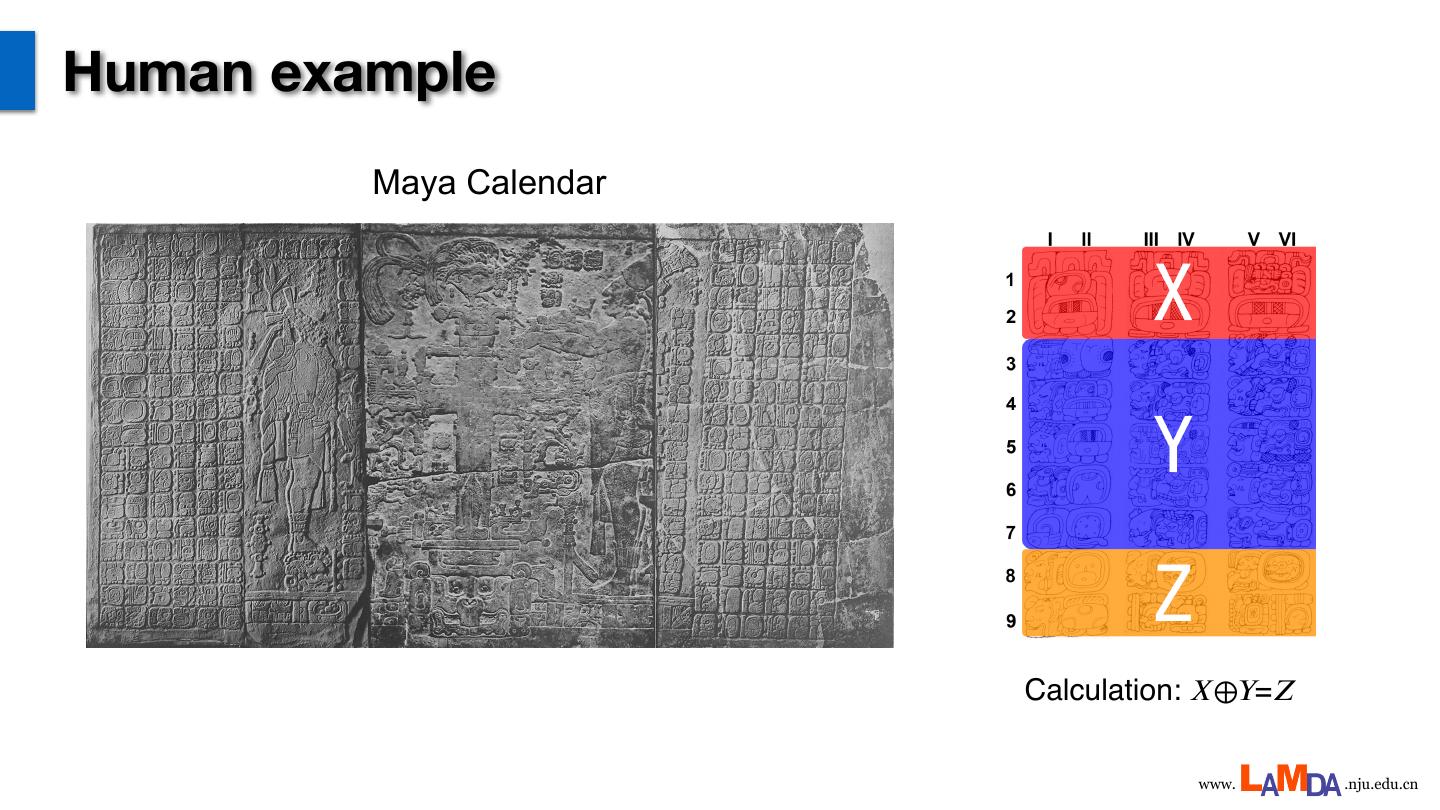
11 .Human example Maya Calendar Calculation: 𝑋⊕𝑌=𝑍 www. .nju.edu.cn 

12 .Unknown perception information www. .nju.edu.cn 

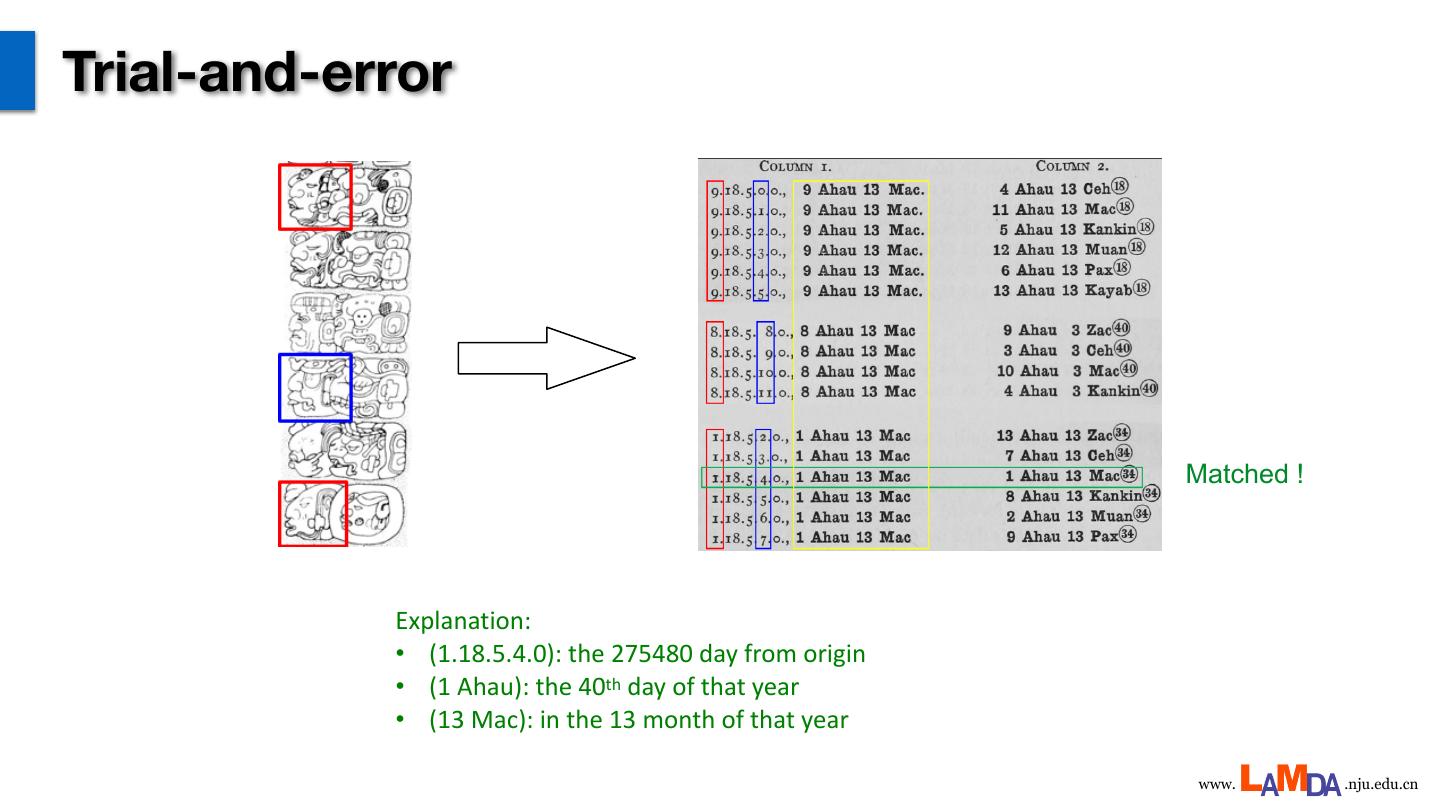
13 .Background knowledge Three Mayan Calendar systems Long Count (玛雅⻓历) date : ? ?. 18 . 5 . ? . 0 They must be consistent à ? What are the ?’s Tzolk‘in (玛雅神历) date : ? Ahau ? Haab‘(玛雅太阳历) date : 13 Mac www. .nju.edu.cn 

14 .Trial-and-error Matched ! Explanation: • (1.18.5.4.0): the 275480 day from origin • (1 Ahau): the 40th day of that year • (13 Mac): in the 13 month of that year www. .nju.edu.cn 

15 .Abductive reasoning Perception Trial-and-error Calculation Glyphs ↦ Numbers Structure: 𝑋⊕𝑌=𝑍 (image) (symbol) Calculation rules: 20-based Equations should be correct Starts from incomplete observations, proceeds to the likeliest possible explana,on for the set www. .nju.edu.cn 

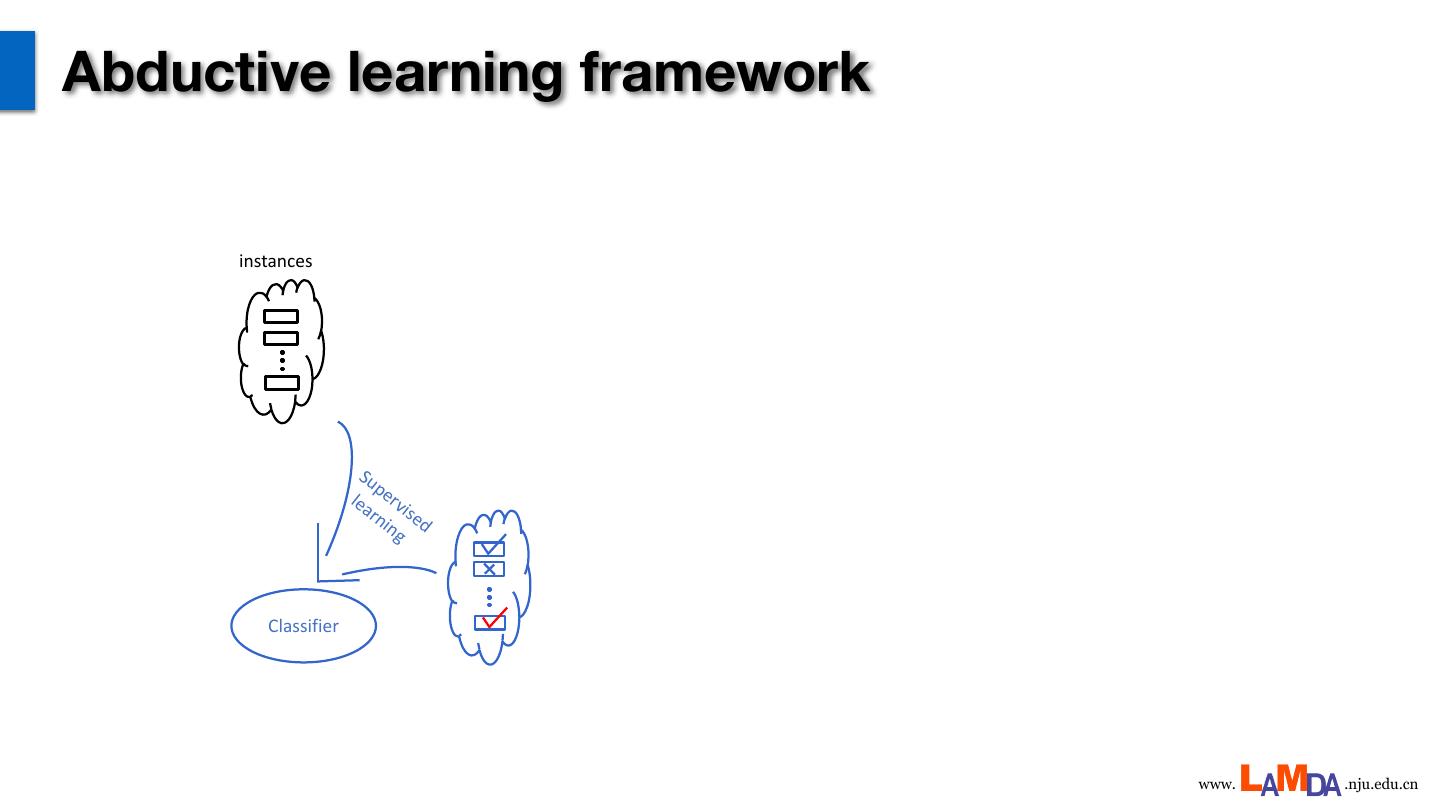
16 .Abductive learning framework instances Su pe lea rv rn ised ing Classifier www. .nju.edu.cn 

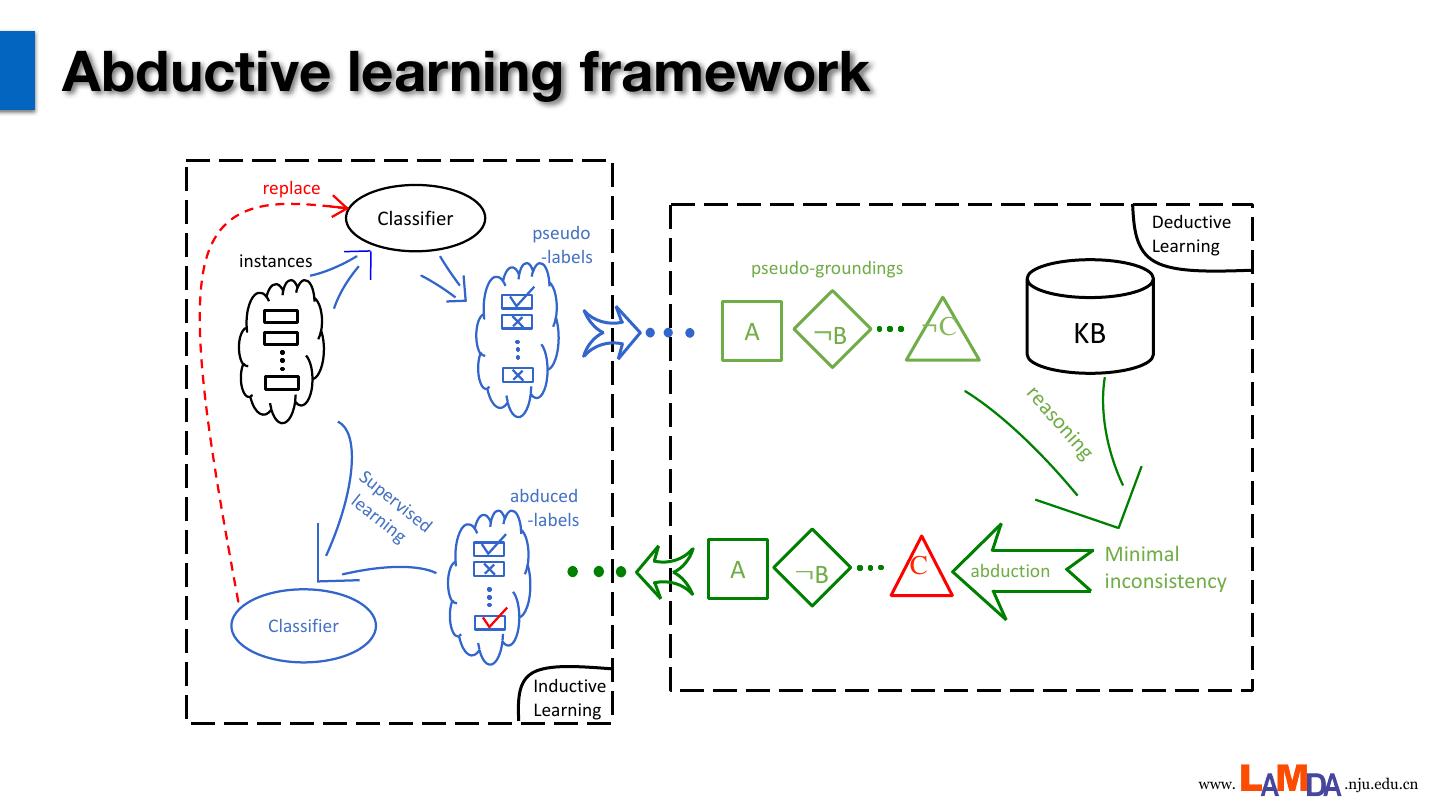
17 .Abductive learning framework replace Classifier Deductive pseudo Learning instances -labels pseudo-groundings A ¬B ¬C KB re as on ing Su pe lea rv abduced rn ised -labels ing Minimal A ¬B C abduction inconsistency Classifier Inductive Learning www. .nju.edu.cn 

18 .An illustrative example The data: DBA (Digital Binary Additive equations); RBA (Random symbol Binary Additive equations) •Untrained perception model (CNN); •Unknown operation rules: add / logical xor / etc. •Learn perception and reasoning jointly; www. .nju.edu.cn 

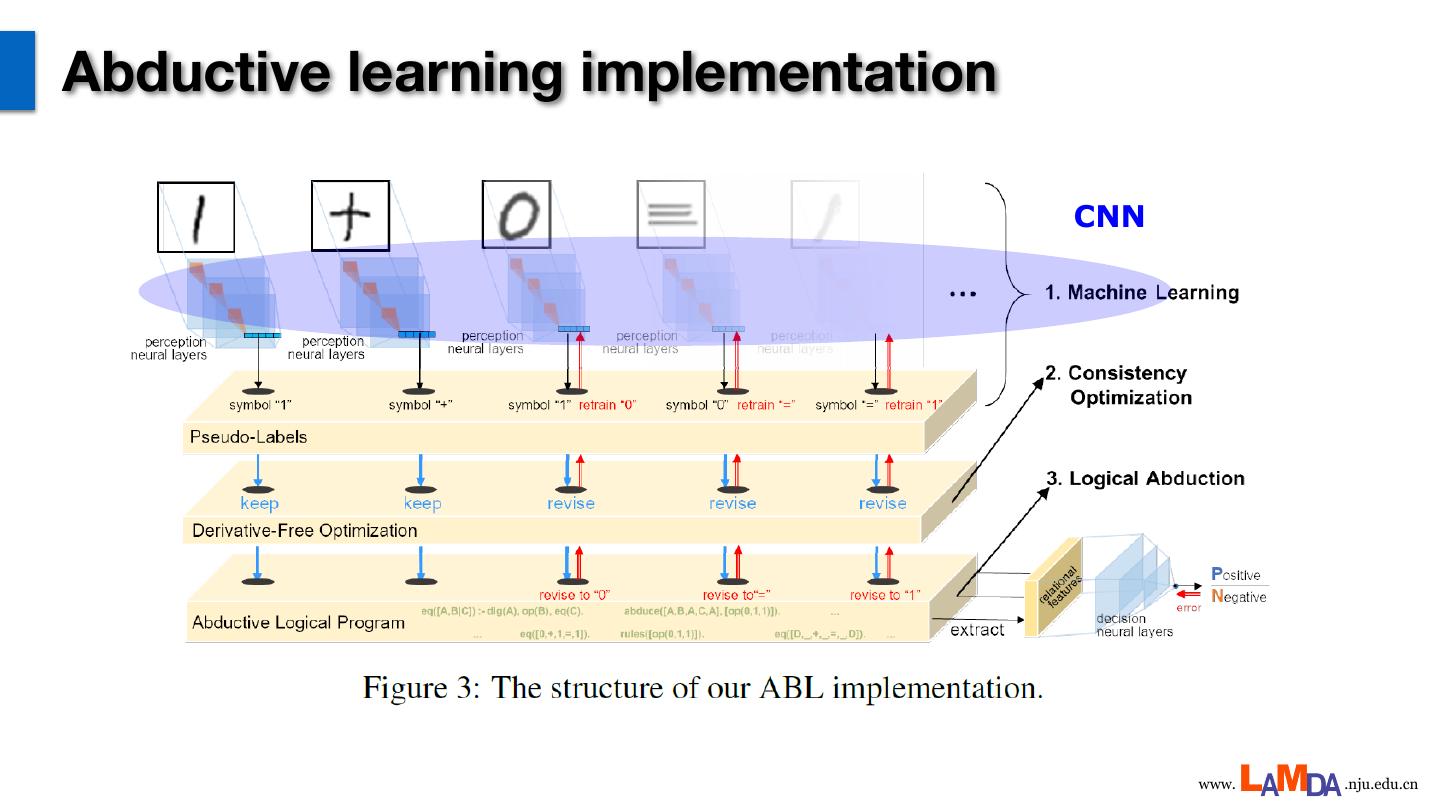
19 .Abductive learning implementation CNN www. .nju.edu.cn 

20 . Background knowledge Equation structure (DCG grammars): Binary operation: • Allequations are X+Y=Z; • Digits are lists of 0 and 1. • Calculated bit-by-bit, from the last to the first; • Allow carries. www. .nju.edu.cn 

21 .Optimization Mark up the “possibly wrong” pseudo-labels, where 𝛿 is a function to guess which perceived symbols are wrong. Maximise consistency by optimizing 𝛿 www. .nju.edu.cn 

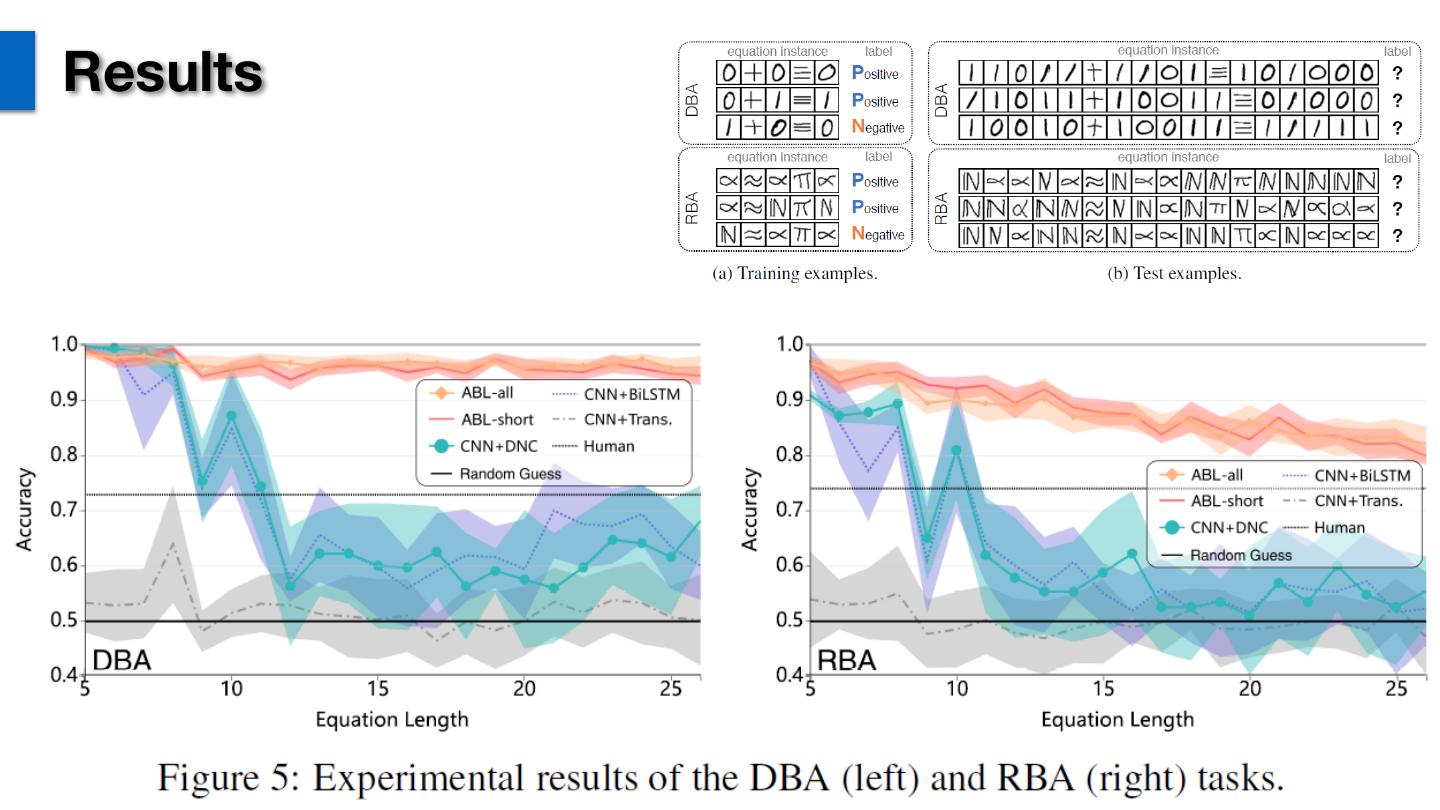
22 .Experiments Setting • Data: length 5-26 equations, each length 300 instances • DBA: MNIST equations; • RBA: Omniglot equations; • Binary addition and exclusive-or. • Compared methods: • ABL-all: Our approach with all training data • ABL-short: Our approach with only length 7-10 equations; • DNC: Memory-based DNN; • Transformer: Attention-based DNN; • BiLSTM: Seq-2-seq baseline; www. .nju.edu.cn 

23 .Results www. .nju.edu.cn 

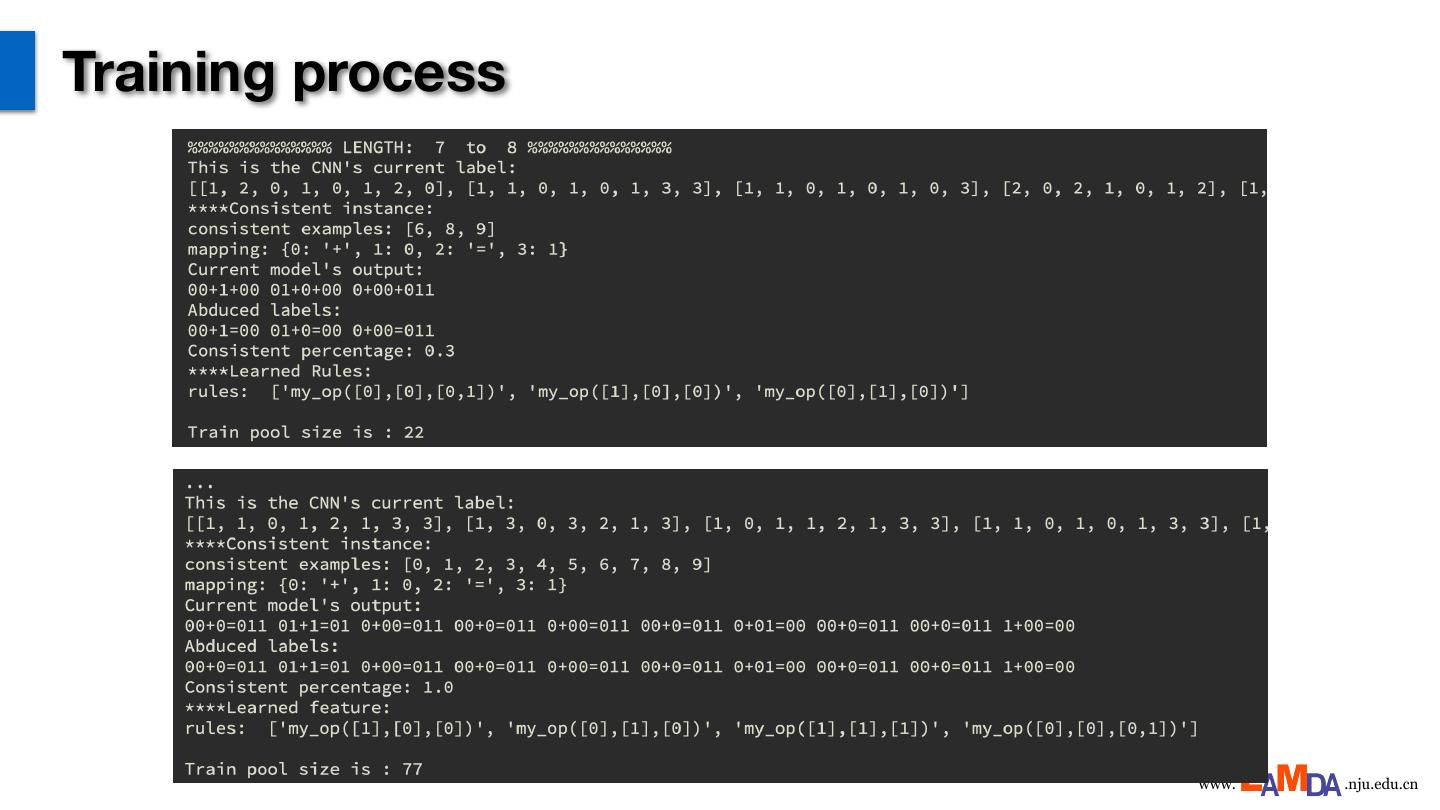
24 .Training process www. .nju.edu.cn 

25 .Perception accuracy www. .nju.edu.cn 

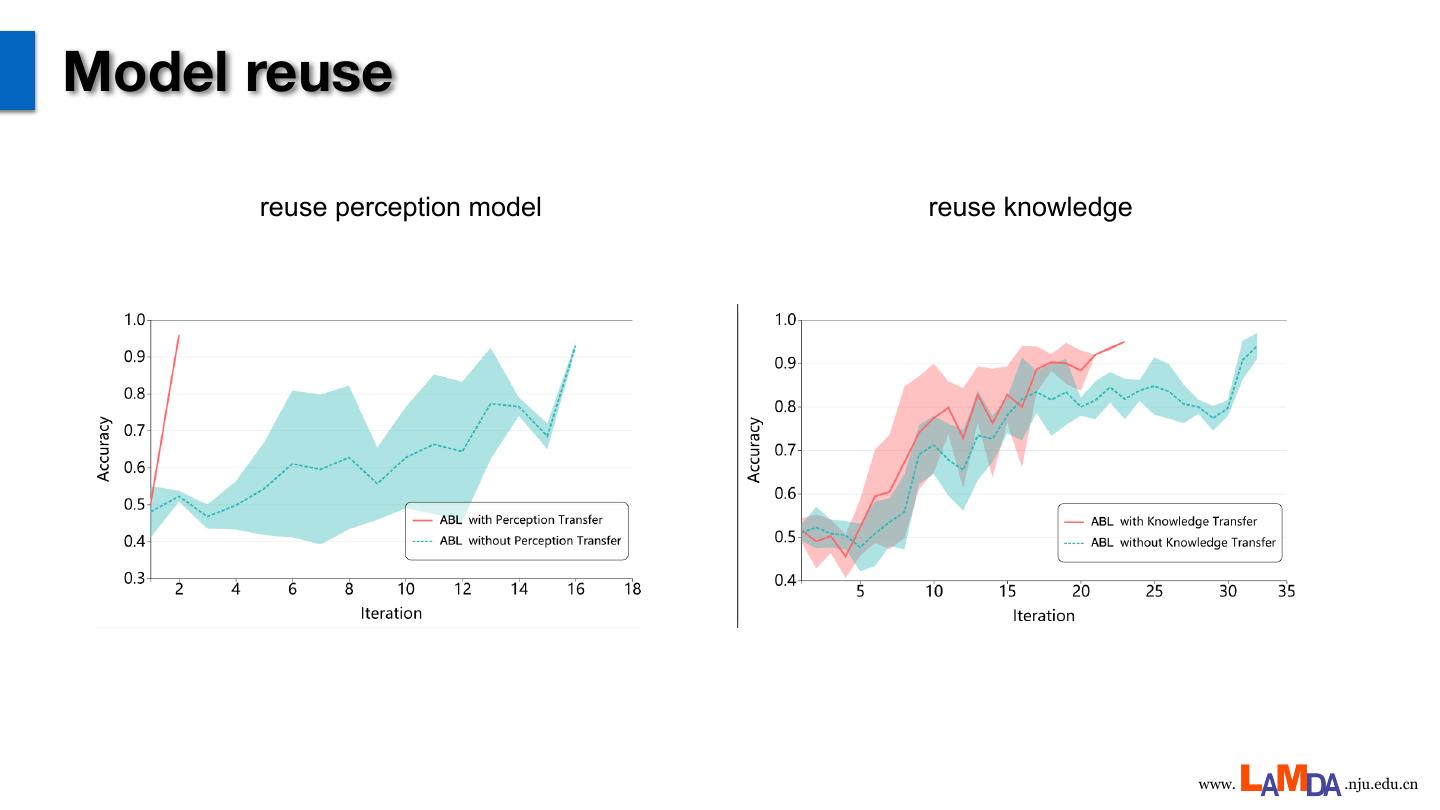
26 .Model reuse reuse perception model reuse knowledge www. .nju.edu.cn 

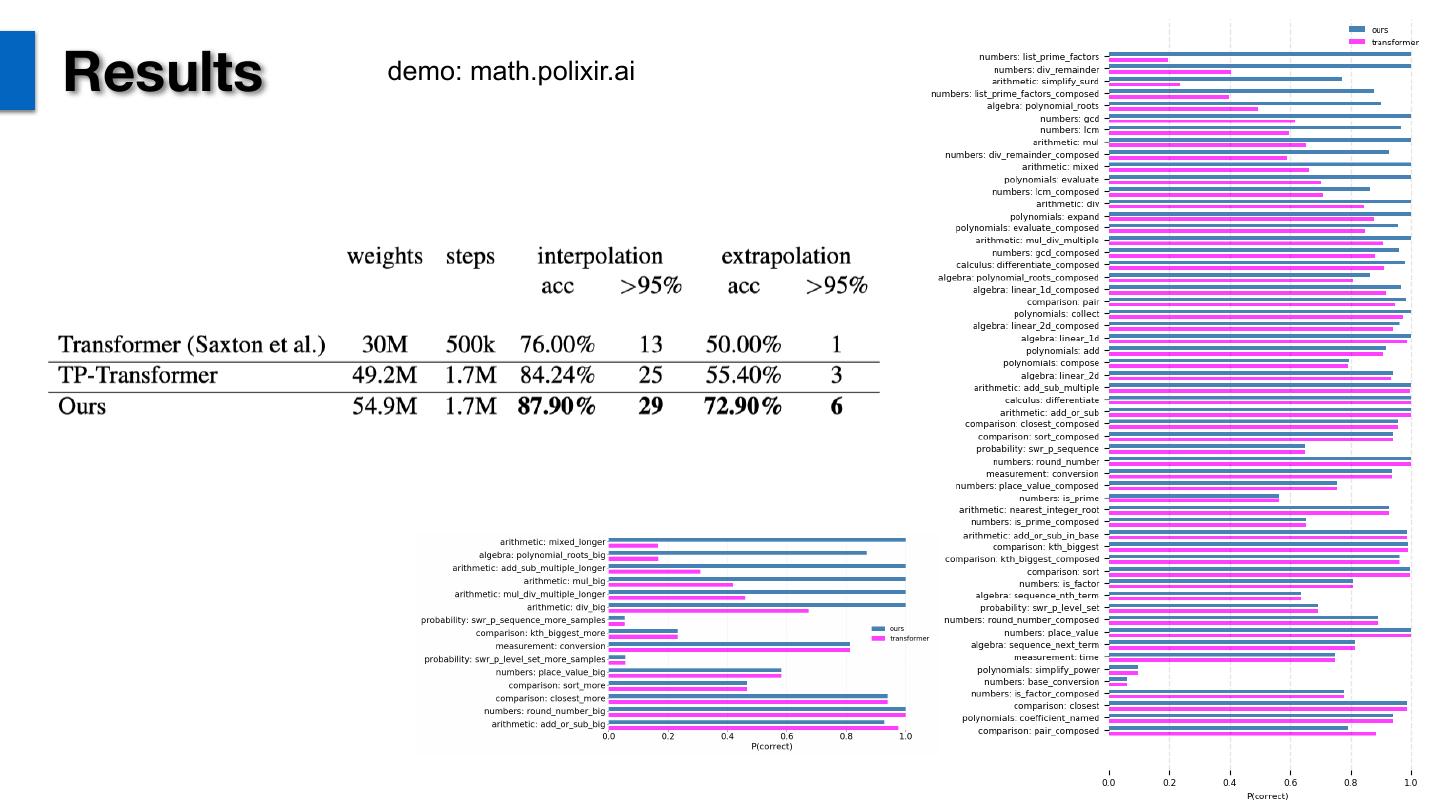
27 . Math QA Data [Amini et al. Mathqa: Towards interpretable math word problem solving with operation-based formalisms. arXiv preprint arXiv:1905.13319, 2019.] www. .nju.edu.cn 

28 .SymPy ◦ Algebras ◦ Lie Algebra ◦ Assumptions ◦ Logic ◦ Calculus ◦ Matrices ◦ Category Theory ◦ Number Theory ◦ Code Generation ◦ Numeric Computation ◦ Combinatorics ◦ Numerical Evaluation ◦ Concrete ◦ ODE ◦ Core ◦ Parsing ◦ Cryptography ◦ PDE ◦ Differential Geometry ◦ Physics ◦ Diophantine ◦ Plotting ◦ Discrete ◦ Polynomial Manipulation ◦ Functions ◦ Printing ◦ Geometry ◦ Series ◦ Holonomic ◦ Sets ◦ Hypergeometric Expansion ◦ Simplify ◦ Inequality Solvers ◦ Solvers ◦ Integrals ◦ Solveset ◦ Computing Integrals using Meijer G-Functions ◦ Stats ◦ The G-Function Integration Theorems ◦ Tensor ◦ The Inverse Laplace Transform of a G-function ◦ Term Rewriting ◦ Implemented G-Function Formulae ◦ Utilities ◦ Interactive ◦ Vector www. .nju.edu.cn 

29 .Abductive search space www. .nju.edu.cn