本地差分隐私及其在机器学习领域应用简介

1 .Nanjing University of Aeronautics and Astronautics 本地差分隐私及其在机器学习 领域应用简介 

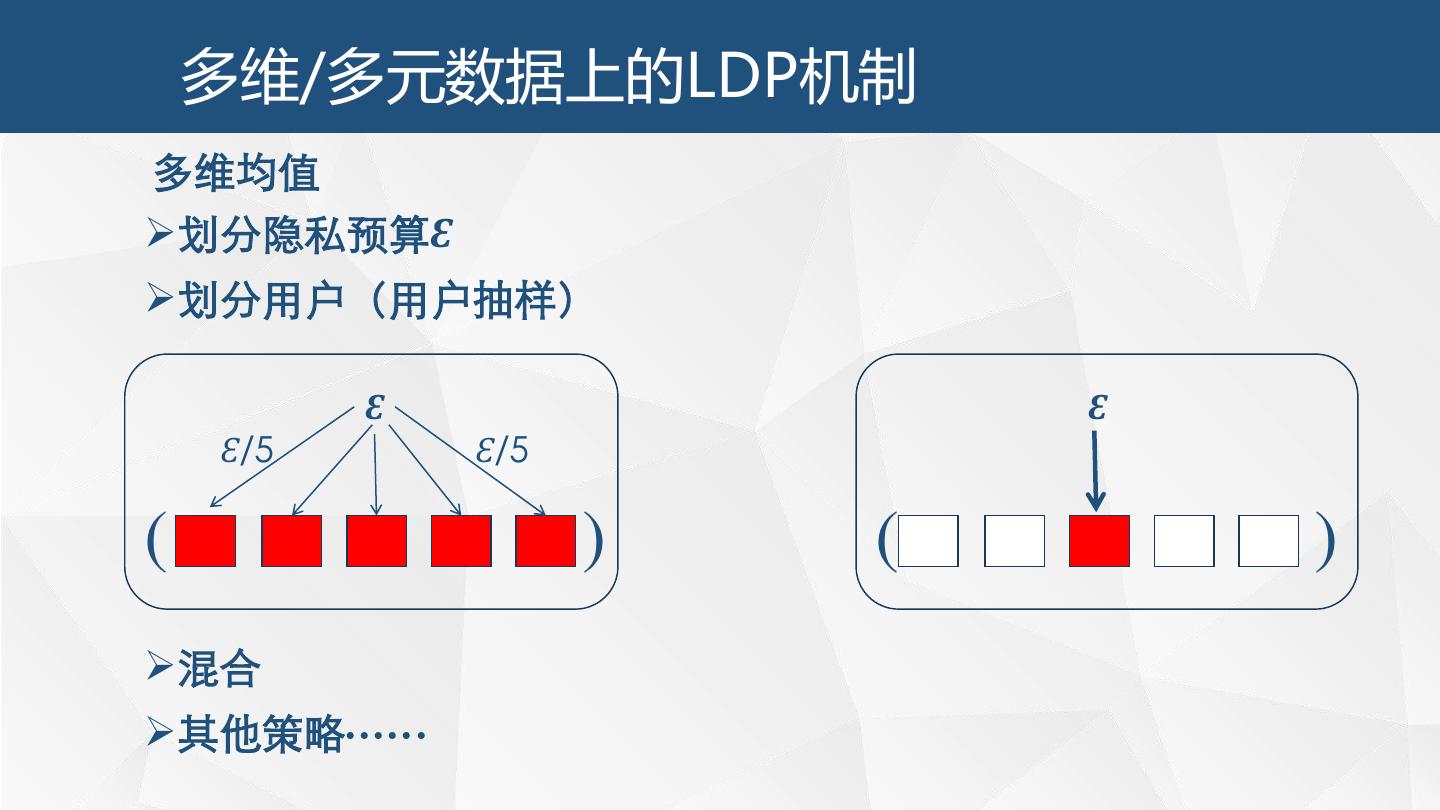
2 . 数据收集过程中的隐私保护  万物互联的时代 • 互联网与智能设备的普及； 1 C • 大量物联网设备的投入使用； • 智能家居；  大规模数据拥有巨大 价值 2A • 用户数据采集与分析； • 改善产品服务，提高用户体验； • 个性化的用户服务/广告 

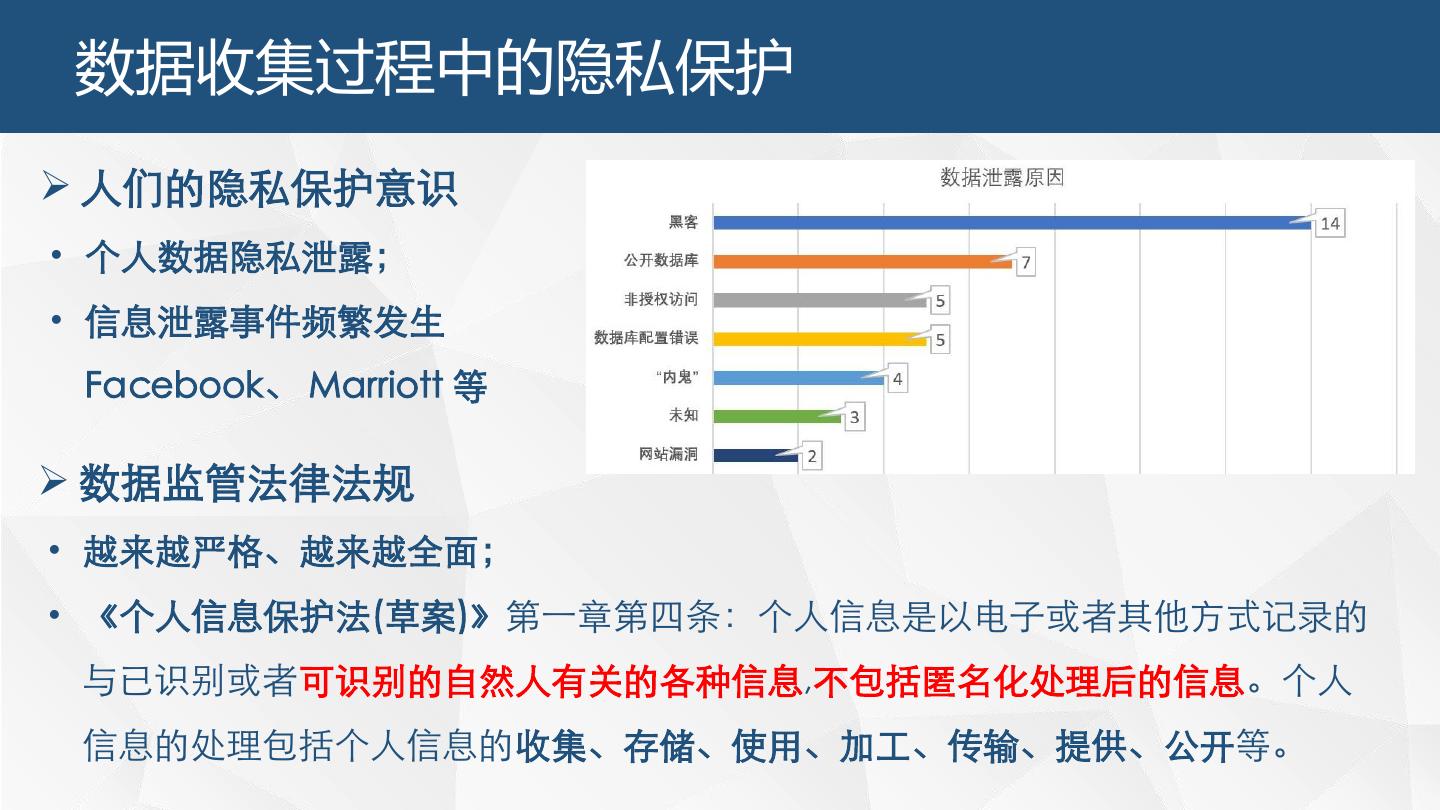
3 . 数据收集过程中的隐私保护  人们的隐私保护意识 • 个人数据隐私泄露； • 信息泄露事件频繁发生 Facebook、 Marriott 等  数据监管法律法规 • 越来越严格、越来越全面； • 《个人信息保护法(草案)》第一章第四条：个人信息是以电子或者其他方式记录的 与已识别或者可识别的自然人有关的各种信息,不包括匿名化处理后的信息。个人 信息的处理包括个人信息的收集、存储、使用、加工、传输、提供、公开等。 

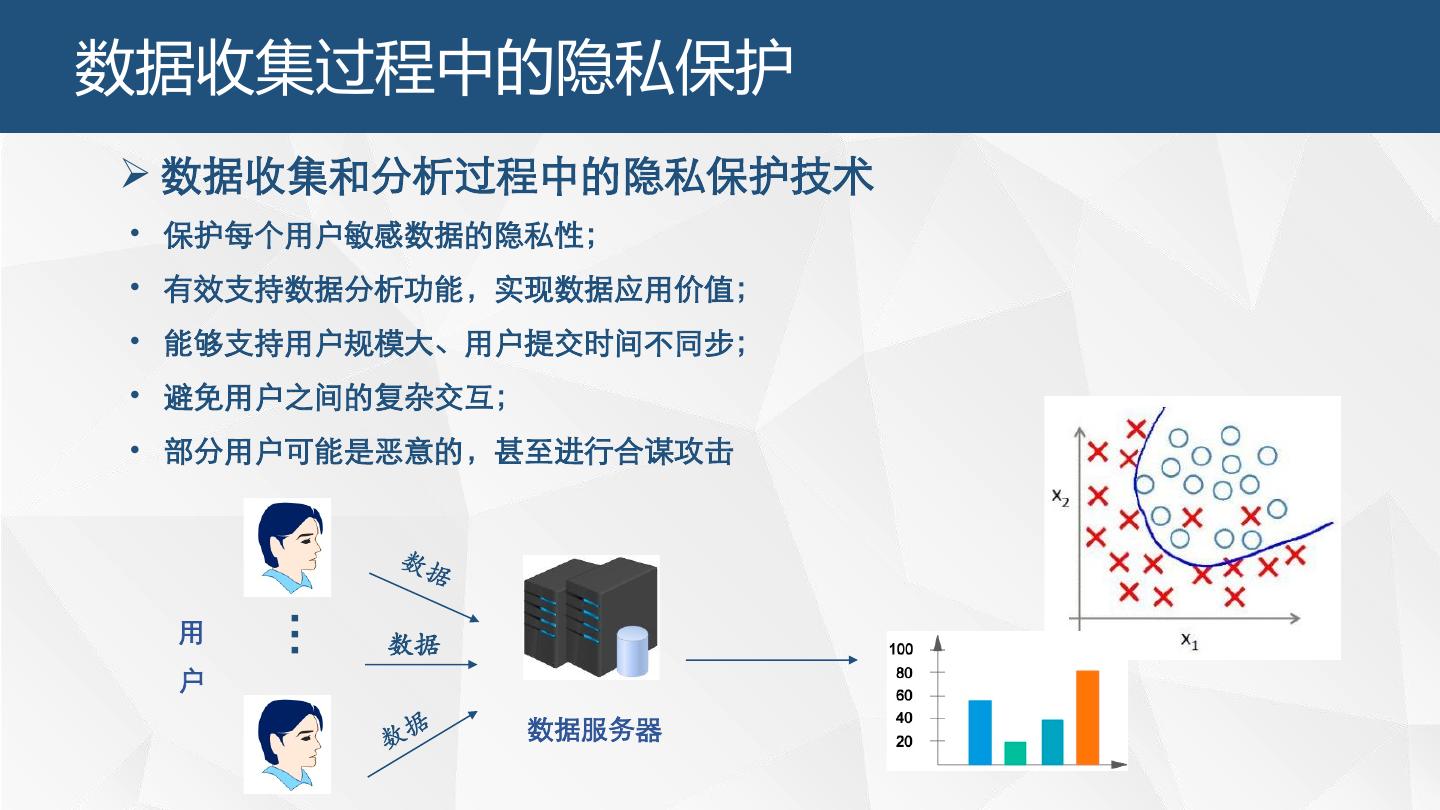
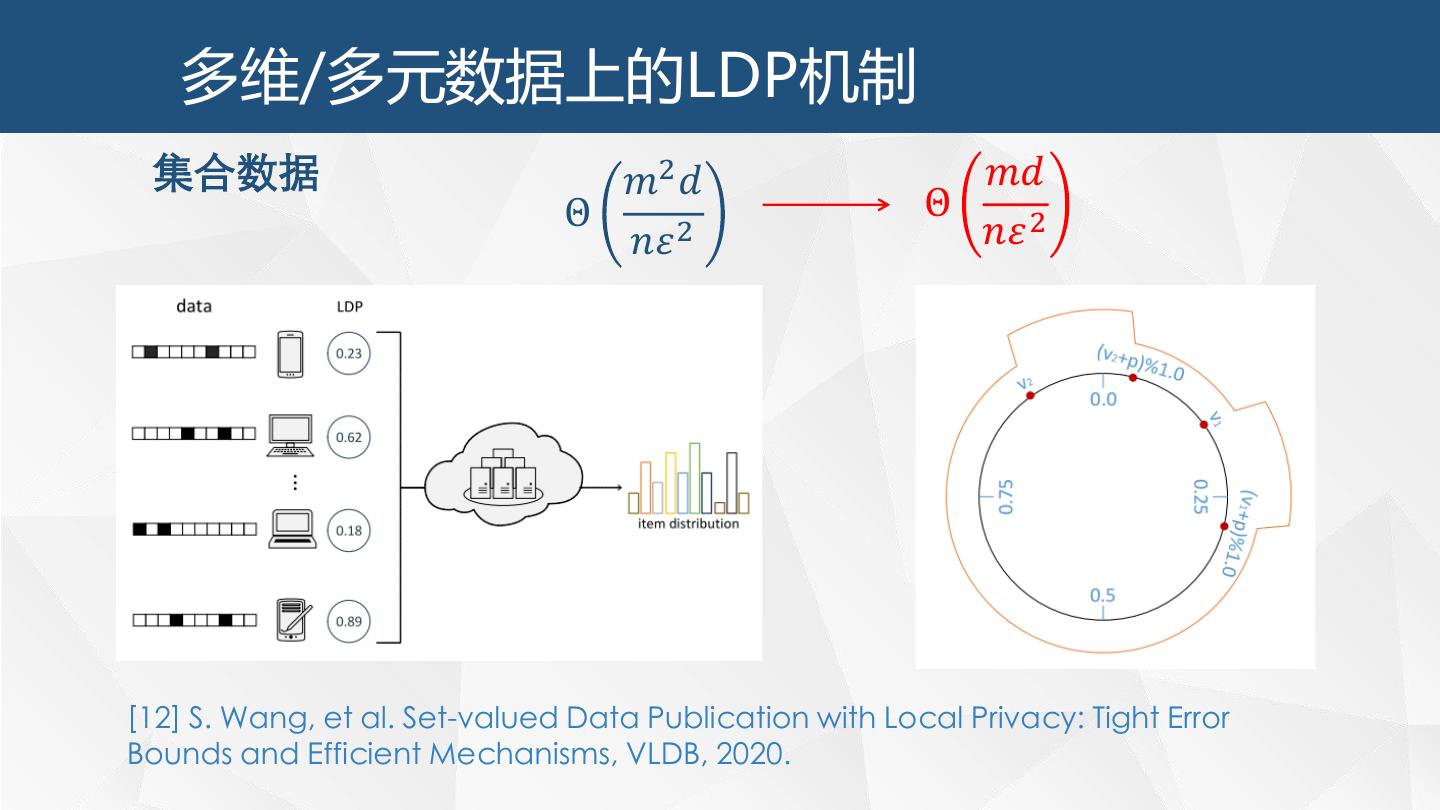
4 .数据收集过程中的隐私保护  数据收集和分析过程中的隐私保护技术 • 保护每个用户敏感数据的隐私性； • 有效支持数据分析功能，实现数据应用价值； • 能够支持用户规模大、用户提交时间不同步； • 避免用户之间的复杂交互； • 部分用户可能是恶意的，甚至进行合谋攻击 … 用 数据 户 数据服务器 

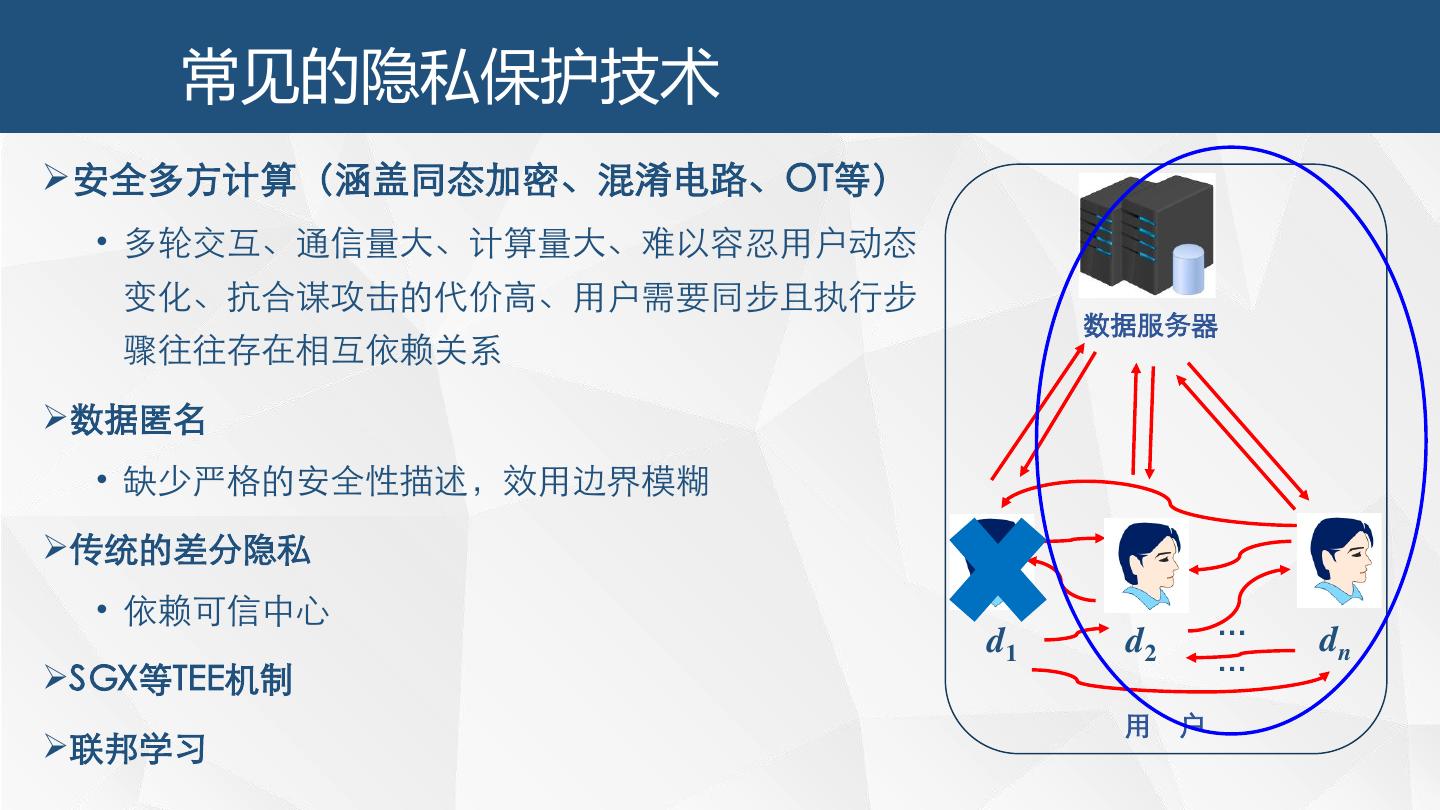
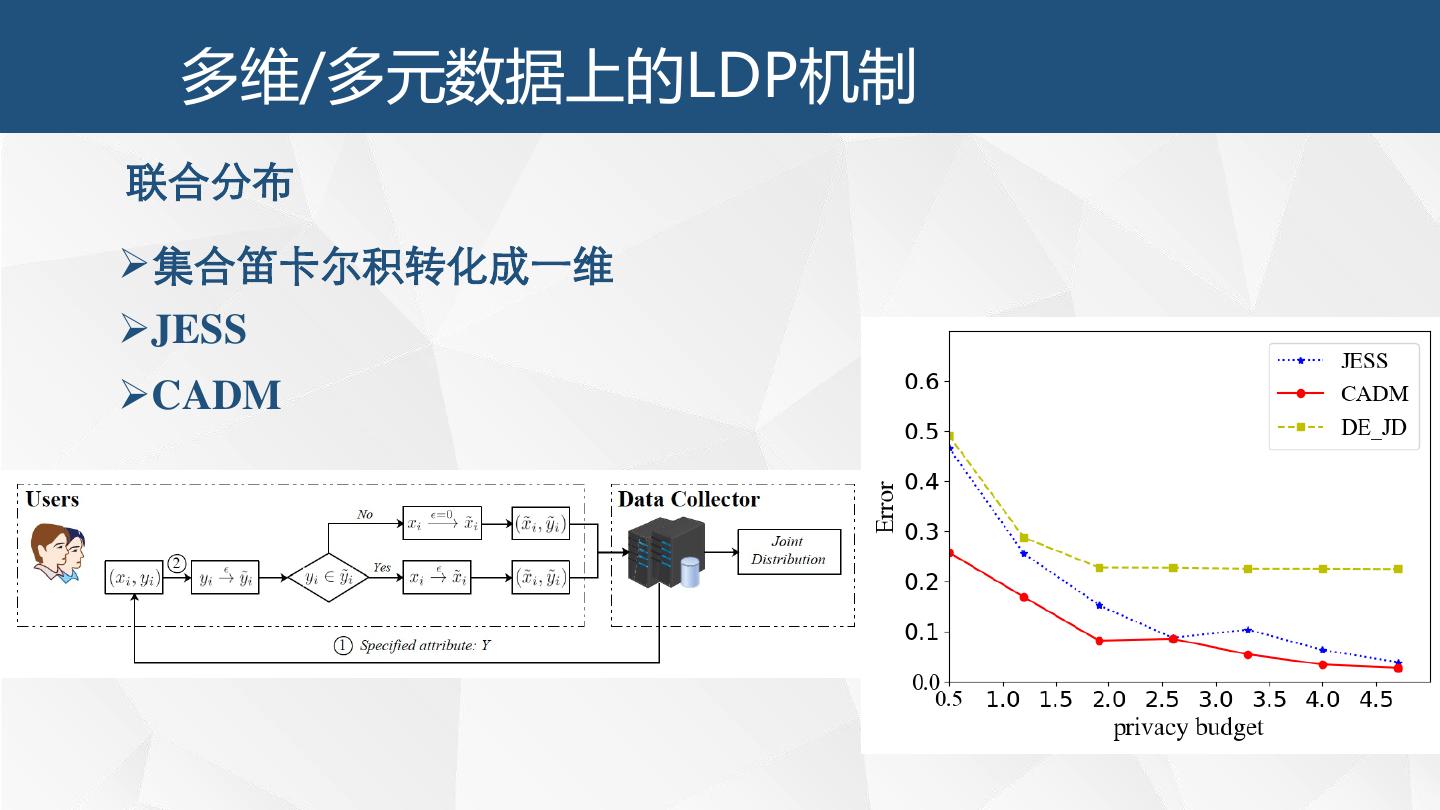
5 . 常见的隐私保护技术 安全多方计算（涵盖同态加密、混淆电路、OT等） • 多轮交互、通信量大、计算量大、难以容忍用户动态 变化、抗合谋攻击的代价高、用户需要同步且执行步 数据服务器 骤往往存在相互依赖关系 数据匿名 • 缺少严格的安全性描述，效用边界模糊 传统的差分隐私 • 依赖可信中心 d1 d2 … dn SGX等TEE机制 … 用 户 联邦学习 

6 . 常见的隐私保护技术 Traditional Differential Privacy（差分隐私） d1 d2 𝒇 𝑫 +noise … 𝑫 𝐃𝐏模块 dn 𝒇 𝑫 数据服务器 可信的 [1] C. Dwork, K. Kenthapadi, F.McSherry, I.Mironov, and M. Naor. Our data, ourselves: Privacy via distributed noise generation. In EUROCRYPT, pages 486–503, 2006. 

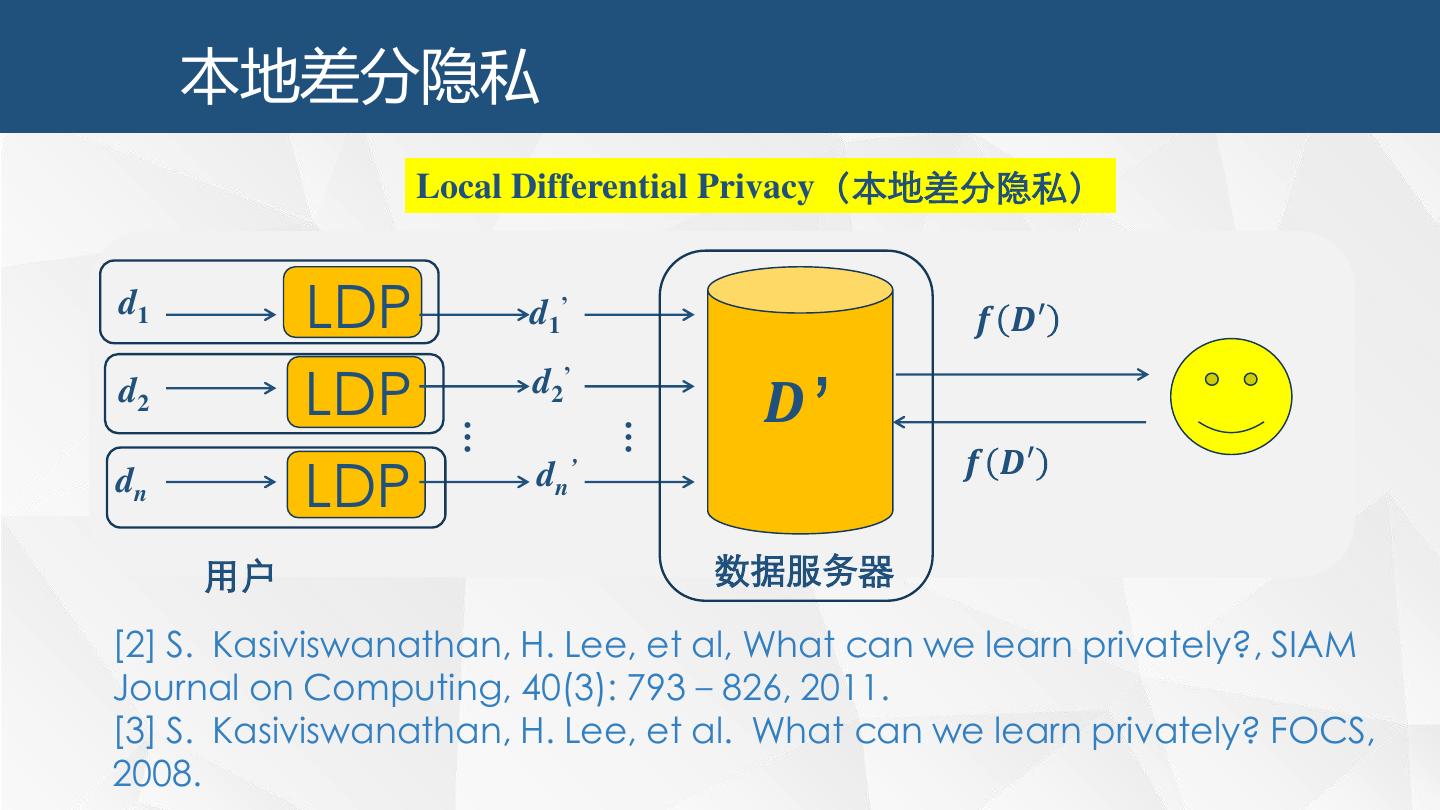
7 . 本地差分隐私 Local Differential Privacy（本地差分隐私） d1 LDP d1’ 𝒇 𝑫′ d2 LDP d2’ 𝑫’ … … LDP dn’ 𝒇 𝑫′ dn 用户 数据服务器 [2] S. Kasiviswanathan, H. Lee, et al, What can we learn privately?, SIAM Journal on Computing, 40(3): 793–826, 2011. [3] S. Kasiviswanathan, H. Lee, et al. What can we learn privately? FOCS, 2008. 

8 . 差分隐私与本地差分隐私 本质上，LDP模型提供了一种评价方法，用 于衡量 di’ 对 di 保护的程度， 攻击者 也就是，攻击者得到 d i’ 时，能够获得di的信息: 获得di’之前 Pr(di) 与 获得di’之后 Pr(di | di’) d i’ 

9 . 差分隐私与本地差分隐私 • 定义（Ɛ-本地化差分隐私, Ɛ-local differential privacy） 算法 𝑅: 𝐼𝑛 → 𝑂𝑢𝑡 是Ɛ-本地化差分隐私的（Ɛ≥0）当且仅当 对于任意两个输入𝒅𝟏 , 𝒅𝟐 ∈ 𝐼𝑛, 任意输出𝒔 ∈ 𝑂𝑢𝑡，满足 𝑷𝒓 𝑹 𝒅𝟏 = 𝒔 ≤ 𝒆𝜺 ∗ 𝑷𝒓[𝑹 𝒅𝟐 = 𝒔] 其中Pr[·]表示事件发生的概率. 即， 𝑒 −𝜀 ∗ 𝑃 𝑟 𝑅 𝑑2 = 𝑠 ≤ 𝑃 𝑟 𝑅 𝑑1 = 𝑠 ≤ 𝑒 𝜀 ∗ 𝑃 𝑟 𝑅 𝑑2 = 𝑠 当概率不为0时， 𝑃 𝑟 𝑅 𝑑1 = 𝑠 𝑒 −𝜀 ≤ ≤ 𝑒𝜀 𝑃 𝑟 𝑅 𝑑2 = 𝑠 

10 . 差分隐私与本地差分隐私 即 𝑃 𝑟 𝑠|𝑑1 𝑒 −𝜀 ≤ ≤ 𝑒𝜀 𝑃 𝑟 𝑠|𝑑2 根据贝叶斯定理， 𝑃𝑟 𝑑1 |𝑠 ∗ 𝑃𝑟 𝑠 = 𝑃𝑟 𝑠|𝑑1 ∗ 𝑃𝑟 𝑑1 𝑃𝑟 𝑑2 |𝑠 ∗ 𝑃𝑟 𝑠 = 𝑃𝑟 𝑠|𝑑2 ∗ 𝑃𝑟 𝑑2 可以得到，  Ɛ限定了d1 和d2 不可区 𝑃𝑟 𝑑1 |𝑠 𝑃𝑟 𝑑1 ∗ 𝑃𝑟 𝑠|𝑑1 分的程度 = 𝑃𝑟 𝑑2 |𝑠 𝑃𝑟 𝑑2 ∗ 𝑃𝑟 𝑠|𝑑2  Ɛ越小，二者越不可区 分 

11 . 差分隐私与本地差分隐私 Ɛ-本地差分隐私（ Ɛ- LDP）  Ɛ 衡量了隐私损失的程度； Ɛ 越小，隐私损失越小  Ɛ 被称为“隐私预算”（privacy budget） 松散的形式: (Ɛ, δ)-本地差分隐私 𝑃𝑟 𝑅 𝑑1 = 𝑠 ≤ 𝑒 𝜀 ∗ 𝑃𝑟 𝑅 𝑑2 = 𝑠 + 𝛿 0≤δ < 1，一般不超过10^{-4} 

12 . 差分隐私与本地差分隐私 • 定义（Ɛ-本地差分隐私, Ɛ-local differential privacy, Ɛ-LDP） • 算法 𝑅: 𝐼𝑛 → 𝑂𝑢𝑡是满足Ɛ-本地差分隐私（Ɛ≥0）当且仅当 • 对于任意两个输入𝑑1 , 𝑑2 ∈ 𝐼𝑛, 任意输出𝑠 ∈ 𝑂𝑢𝑡，满足以下公式 𝑃𝑟 𝑅 𝑑1 = 𝑠 ≤ 𝑒 𝜀 ∗ 𝑃𝑟[𝑅 𝑑2 = 𝑠] 其中Pr[·]表示事件发生的概率. 组合特性 已知存在𝑆个满足𝜖𝑖 −LDP的随机算法𝐴𝑖 ，𝑖 ∈ {1, … , 𝑆}，数据D经S 个随机 算法处理之后的输出结果序列： 𝐴1 𝐷 , … , 𝐴𝑆 𝐷 ，满足 σ𝑆𝑠=1 𝜖𝑠 −LDP 

13 . 本地差分隐私 近几年，LDP在学术界和工业届都得到了很多的关注  Google: RAPPOR, SODA’19，……  Apple: CMS，系列专利  微软：NIPS 2017  US Census Bureau： Differential Privacy in the 2020 US Census  阿里巴巴：DataTrust，SIGMOD 2019  IBM: TIFS 2017  …… 

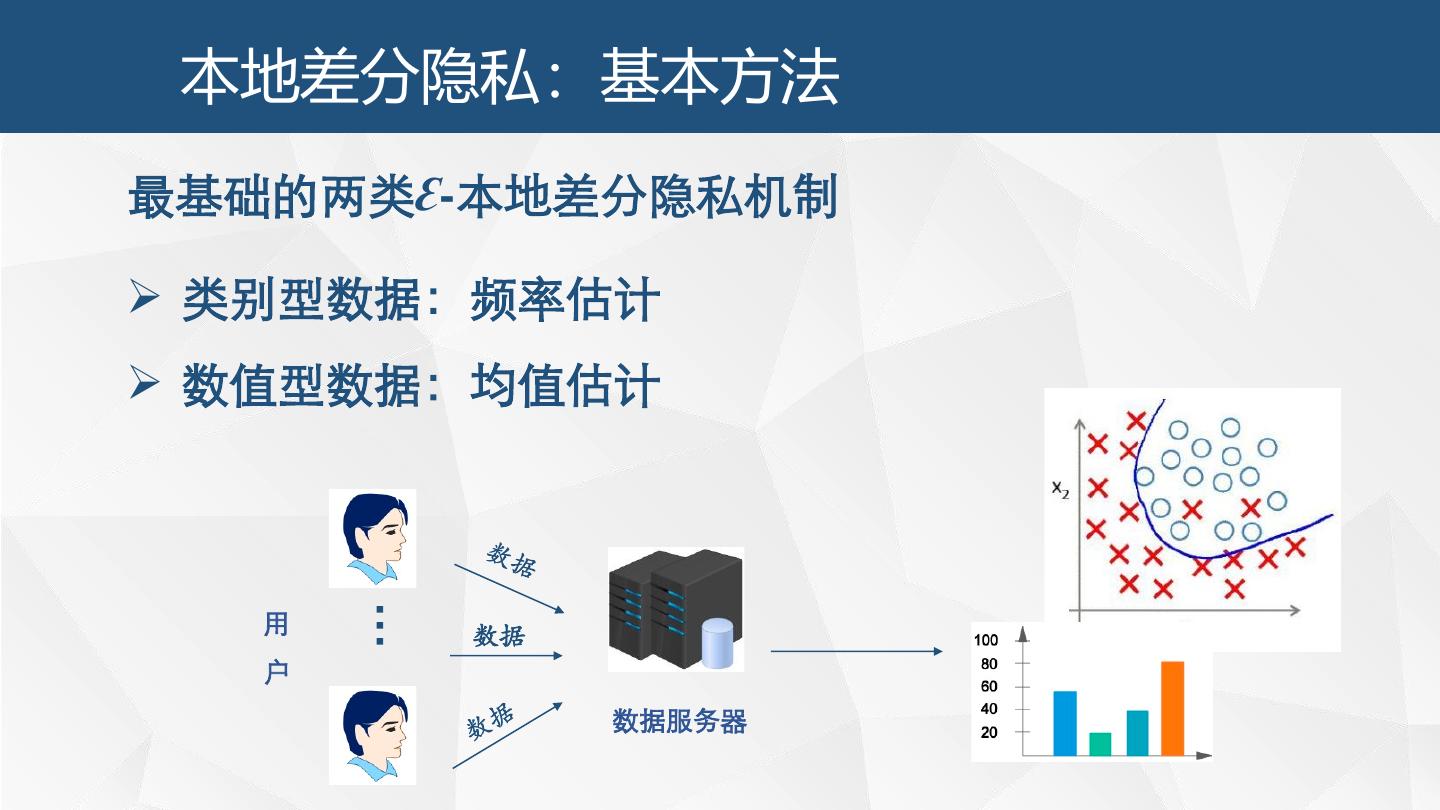
14 . 本地差分隐私：基本方法 最基础的两类Ɛ-本地差分隐私机制  类别型数据：频率估计  数值型数据：均值估计 … 用 数据 户 数据服务器 

15 .本地差分隐私：基本方法 Ɛ-本地差分隐私机制主要包含两个模块：  编码+扰动: Xi = Encode(di) 每个用户单独完成 di’ = Perturb(Xi) 服务器完成  聚合+后处理：𝒇(d ෠ 1, d2,…, dn) = Aggregate(d1’, d2’,…, dn’) 

16 . 二值频率估计 二值频数统计问题 • 被调查者可能被问到隐私问题，如：“你是否曾经考试作弊？” • 被调查者回复: ‘是’ / ‘否’; Server希望得到真实回答为‘是’的比例 ρ 

17 . 二值频率估计 随机响应(Randomised Response, RR) 编码: 真实回复表示为 𝐴𝑖 ∈ {1, 0}, 其中Ai=1表示 ‘是’, 𝐴𝑖 =0表示‘否’ 𝐴𝑖 , 以 𝑝的概率 扰动: 提交的回复𝐴′𝑖 =ቊ 1 − 𝐴𝑖 , 以1 − 𝑝的概率 𝑒𝜀 为了满足Ɛ-LDP： 1−𝑝和𝑝 ≤ 𝜀 𝑒 +1 [4] S. L. Warner, Randomized response: a survey technique for eliminating evasive answer bias, Journal of the American Statistical Association, 1965 [5] N. Holohan, D. Leith, O. Mason. Optimal Differentially Private Mechanisms for Randomised Response. IEEE TIFS, 2017. 

18 .二值频率估计 假设真实回答为“是”的比例： 𝜌 实际回答为“是”的比例为：𝜌′ 𝜌′ 𝑝−1 𝜌′ = 𝜌𝑝 + (1 − 𝜌)(1 − 𝑝) 𝜌ො = 2𝑝−1 + 2𝑝−1 𝜌 的无偏估计 

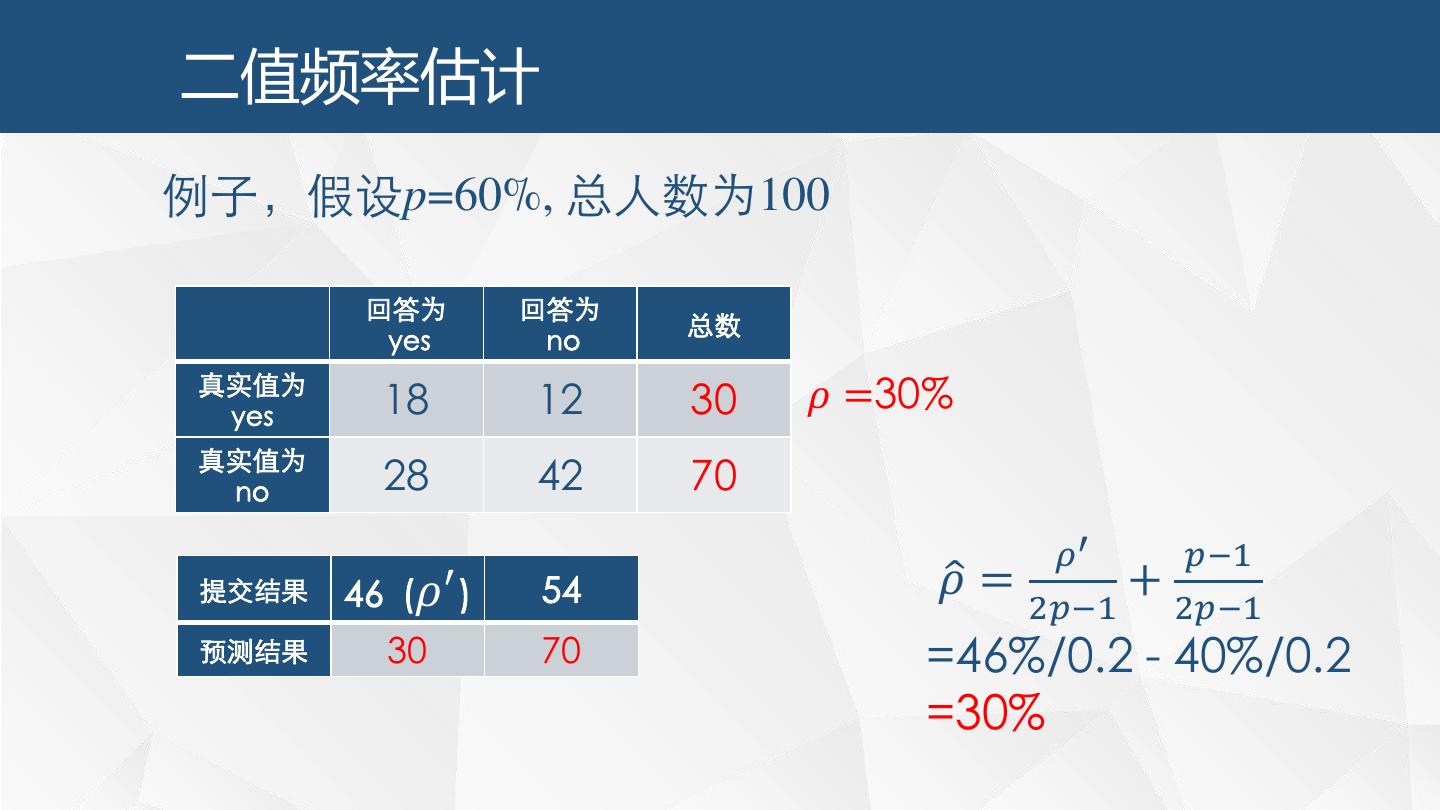
19 .二值频率估计 例子，假设p=60%, 总人数为100 回答为 回答为 总数 yes no 真实值为 yes 18 12 30 𝜌 =30% 真实值为 no 28 42 70 𝜌′ 𝑝−1 提交结果 46 (𝜌 ′ ) 54 𝜌ො = + 2𝑝−1 2𝑝−1 预测结果 30 70 =46%/0.2 - 40%/0.2 =30% 

20 . 多值频率估计 多值频数统计：真实回答范围为{1, 2, …, d} 直接编码(k-RR): v∈{1, 2, …, d}是某个真实回答，Encode(v) = v, 相应地， 𝑒𝜀 𝜀 , 当 𝑖 = 𝑣时 Pr[Perturb 𝑣 = 𝑖] = 𝑒 + 𝑑 − 1 1 𝜀 , 当 𝑖 ≠ 𝑣时 𝑒 +𝑑−1 [6] Kairouz P, Oh S, Viswanath P. Extremal mechanisms for local differential privacy. Advances in neural information processing systems (NIPS). 2014 : 2879-2887. 

21 . 多值频率估计 多值频数统计：真实回答范围为{1, 2, …, d} 直接编码: 对于任意t∈{1, 2, …, d} ，ft’表示提交值为t的比例 𝑒𝜀 𝑝1 = , 令ቐ 𝜀 𝑒 +𝑑−1 则， 𝑓𝑡′ − 𝑝0 1 𝑓෡𝑡 = 为真实分布ft的无偏估计 𝑝0 = , 𝑝1 − 𝑝0 𝑒 𝜀 +𝑑−1 

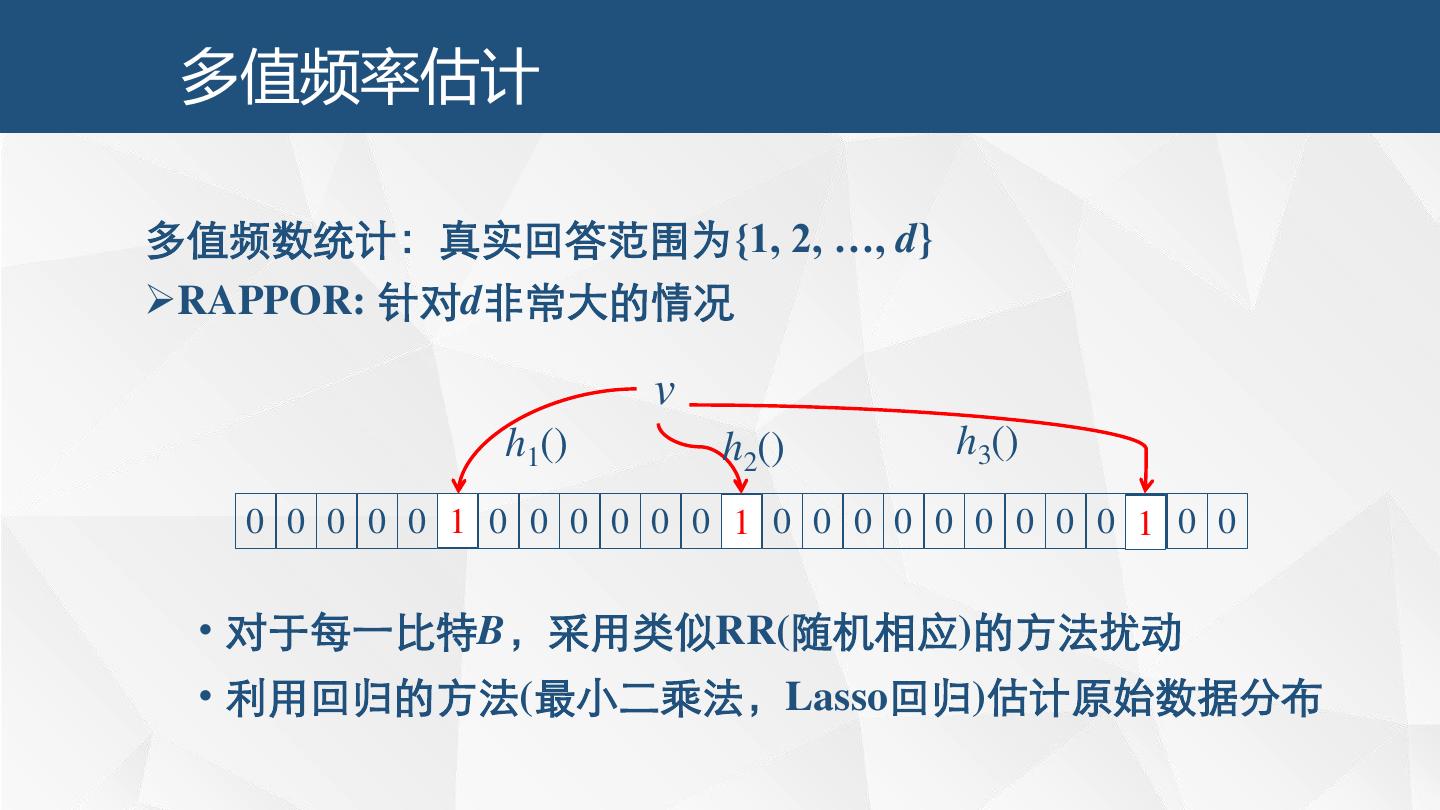
22 . 多值频率估计 第v比特等于1 多值频数统计：真实回答范围为{1, 2, …, d} One-hot编码(k-RAPPOR): Encode(v) = (0 , …, 0, 1, 0, …, 0), d比特 • 对于每一比特，分别采用类似RR(随机响应)的方法扰动 • 每一列单独估计其中“1”的频数 [7] Erlingsson U ., Pihur V., Korolova A. RAPPOR: Randomized aggregatable privacy preserving ordinal response. ACM CCS, 2014: 1054–1067. 

23 . 多值频率估计 多值频数统计：真实回答范围为{1, 2, …, d} RAPPOR: 针对d非常大的情况 v h1() h2() h3() 0 0 0 0 0 10 0 0 0 0 0 0 01 0 0 0 0 0 0 0 0 0 10 0 0 • 对于每一比特B，采用类似RR(随机相应)的方法扰动 • 利用回归的方法(最小二乘法，Lasso回归)估计原始数据分布 

24 . 多值频率估计 多值频数统计：真实回答范围为{1, 2, …, d} 子集选择机制: v∈{1, 2, …, d}是某个真实的回答，Encode(v) = v, 变换之后提交的是{1, 2, …, d}的一个子集Sv，并设定|Sv|为k. 其中子集Sv包含v的概率为， 𝑘𝑒 𝜀 𝑝1 = 𝜀 𝑘𝑒 + 𝑑 − 𝑘 变换步骤是：先确定Sv是否包含v，然后以均匀概率选择其余k或k-1个其 他元素. [8] Min Ye, Alexander Barg. Optimal Schemes for Discrete Distribution Estimation under Locally Differential Privacy, , IEEE Transactions on Information Theory, 2018. 

25 . 多值频率估计 多值频数统计：真实回答范围为{1, 2, …, d} 子集选择机制: 对于任意t∈{1, 2, …, d} ，ft’表示提交值包含t的用户 比例. 𝑘𝑒 𝜀 𝑝1 = 𝜀 , 𝑓𝑡′ − 𝑝0 令ቐ 𝑘𝑒 +𝑑−𝑘 𝑘−𝑝1 则， 𝑓෡𝑡 = 为真实分布ft的无偏估计 𝑝0 = , 𝑝1 − 𝑝0 𝑑−1 k的最优值为： 𝑑 𝑘= 𝜀 𝑒 +1 

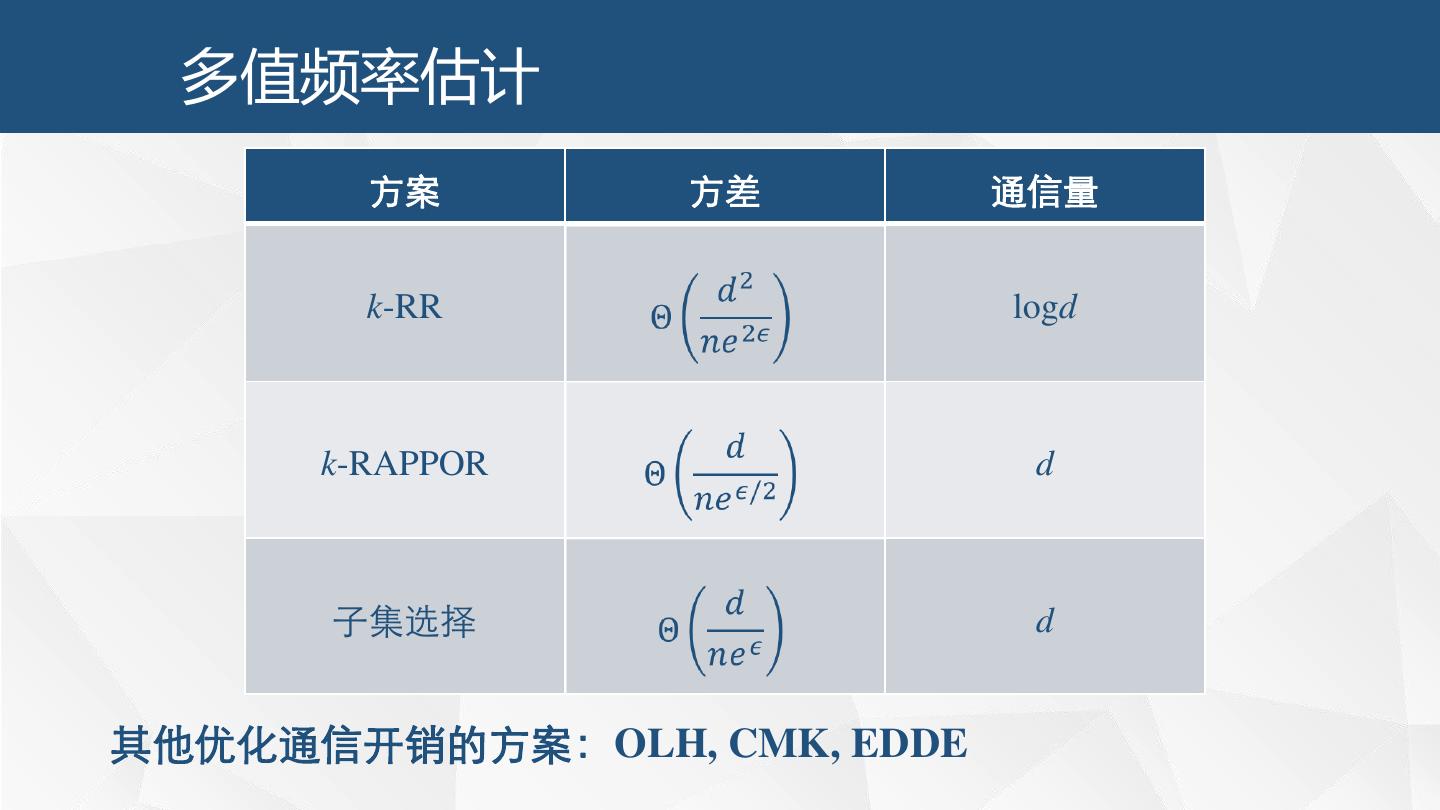
26 . 多值频率估计 方案 方差 通信量 k-RR logd k-RAPPOR d 子集选择 d 其他优化通信开销的方案：OLH, CMK, EDDE 

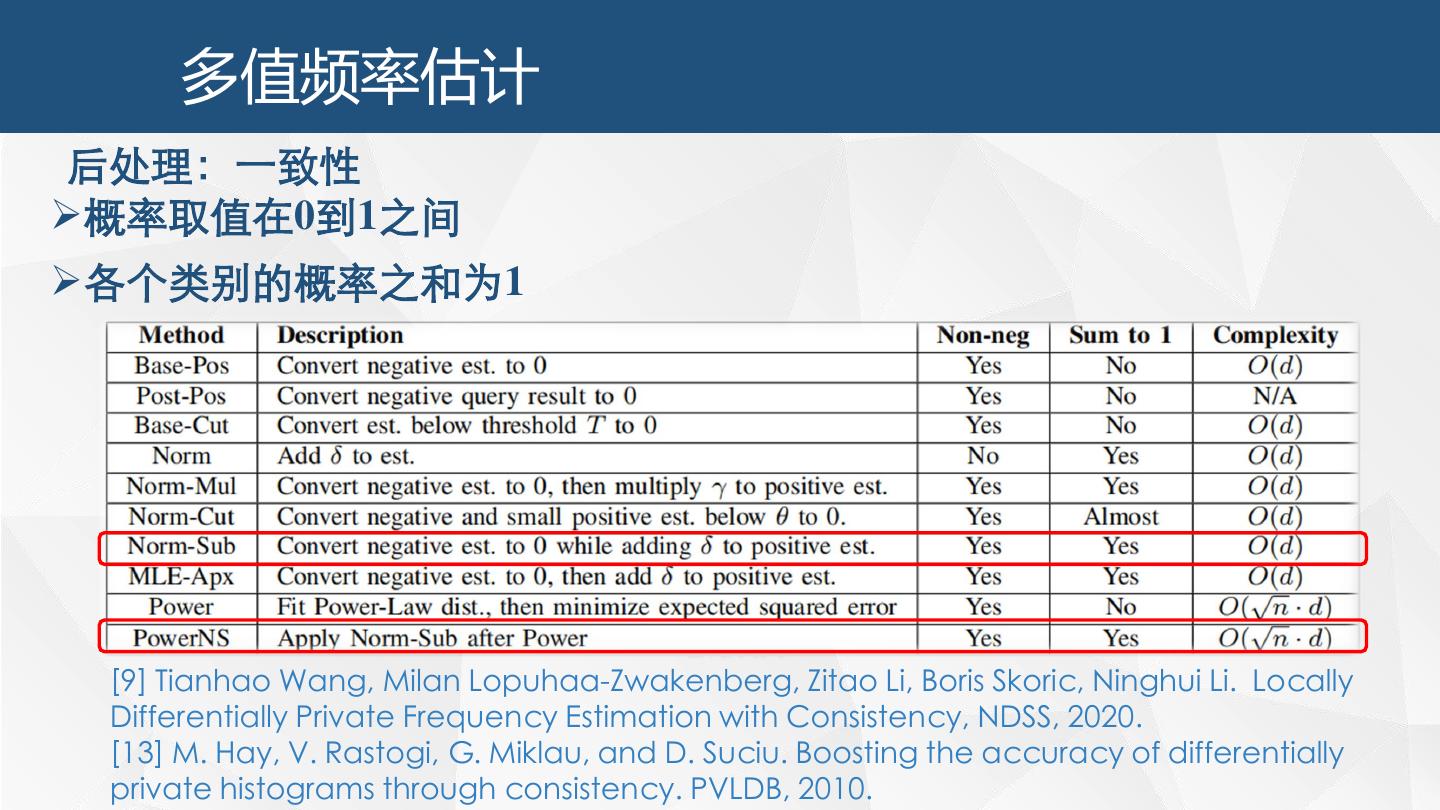
27 . 多值频率估计 后处理：一致性 概率取值在0到1之间 各个类别的概率之和为1 [9] Tianhao Wang, Milan Lopuhaa-Zwakenberg, Zitao Li, Boris Skoric, Ninghui Li. Locally Differentially Private Frequency Estimation with Consistency, NDSS, 2020. [13] M. Hay, V. Rastogi, G. Miklau, and D. Suciu. Boosting the accuracy of differentially private histograms through consistency. PVLDB, 2010. 

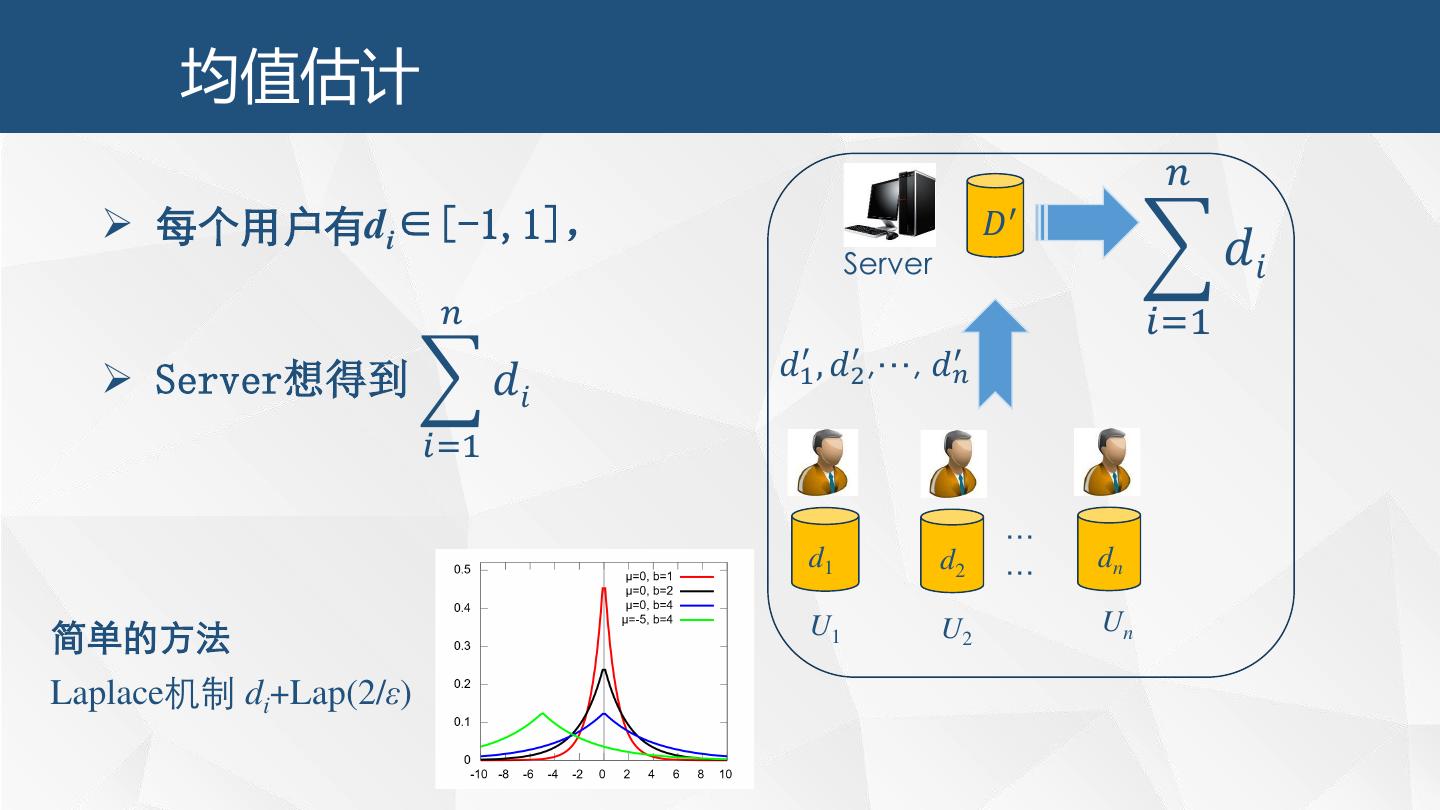
28 . 均值估计 𝑛  每个用户有di∈[-1,1]， 𝐷′ Server ෍ 𝑑𝑖 𝑛 𝑖=1  Server想得到 ෍ 𝑑𝑖 𝑑1′ , 𝑑2′ ,…, 𝑑𝑛′ 𝑖=1 … d1 d2 … dn 简单的方法 U1 U2 Un Laplace机制 di+Lap(2/ε) 

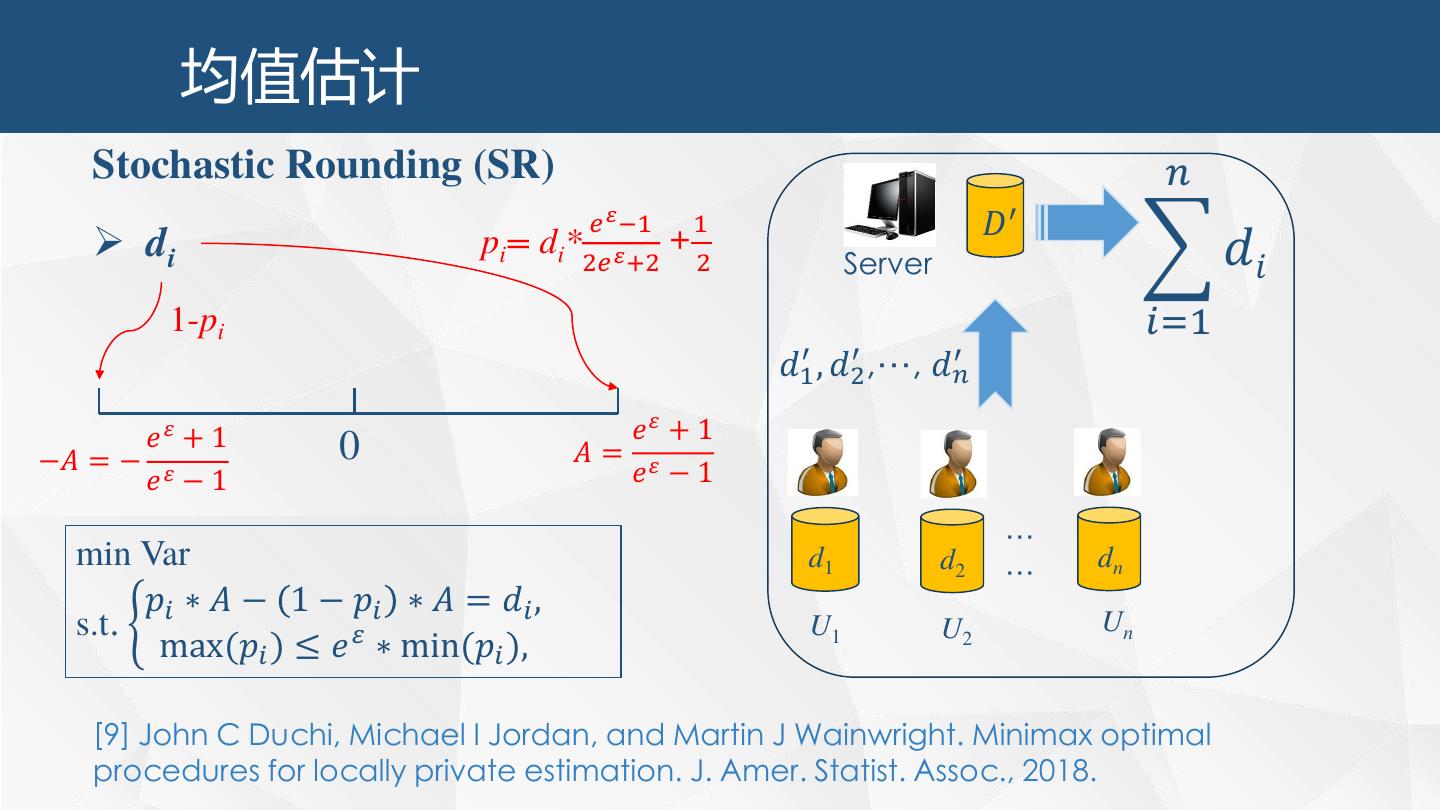
29 . 均值估计 Stochastic Rounding (SR) 𝑛 𝑒 𝜀 −1 1 𝐷′  di p i= d i* 𝜀 + ෍ 𝑑𝑖 2𝑒 +2 2 Server 1-pi 𝑖=1 𝑑1′ , 𝑑2′ ,…, 𝑑𝑛′ 𝑒𝜀 + 1 𝑒𝜀 + 1 −𝐴 = − 𝜀 0 𝐴= 𝜀 𝑒 −1 𝑒 −1 … min Var d1 d2 … dn 𝑝𝑖 ∗ 𝐴 − 1 − 𝑝𝑖 ∗ 𝐴 = 𝑑𝑖 , s.t. ቊ U1 U2 Un max(𝑝𝑖 ) ≤ 𝑒 𝜀 ∗ min(𝑝𝑖 ), [9] John C Duchi, Michael I Jordan, and Martin J Wainwright. Minimax optimal procedures for locally private estimation. J. Amer. Statist. Assoc., 2018.