deep_rl

1 .Deep Reinforcement Learning David Silver, Google DeepMind 

2 .Reinforcement Learning: AI = RL RL is a general-purpose framework for artificial intelligence RL is for an agent with the capacity to act Each action influences the agent’s future state Success is measured by a scalar reward signal RL in a nutshell: Select actions to maximise future reward We seek a single agent which can solve any human-level task The essence of an intelligent agent 

3 .Agent and Environment state action st at At each step t the agent: Receives state st Receives scalar reward rt reward rt Executes action at The environment: Receives action at Emits state st Emits scalar reward rt 

4 .Examples of RL Control physical systems: walk, fly, drive, swim, ... Interact with users: retain customers, personalise channel, optimise user experience, ... Solve logistical problems: scheduling, bandwidth allocation, elevator control, cognitive radio, power optimisation, .. Play games: chess, checkers, Go, Atari games, ... Learn sequential algorithms: attention, memory, conditional computation, activations, ... 

5 .Policies and Value Functions Policy π is a behaviour function selecting actions given states a = π(s) Value function Q π (s, a) is expected total reward from state s and action a under policy π Q π (s, a) = E rt+1 + γrt+2 + γ 2 rt+3 + ... | s, a “How good is action a in state s?” 

6 .Approaches To Reinforcement Learning Policy-based RL Search directly for the optimal policy π ∗ This is the policy achieving maximum future reward Value-based RL Estimate the optimal value function Q ∗ (s, a) This is the maximum value achievable under any policy Model-based RL Build a transition model of the environment Plan (e.g. by lookahead) using model 

7 .Deep Reinforcement Learning Can we apply deep learning to RL? Use deep network to represent value function / policy / model Optimise value function / policy /model end-to-end Using stochastic gradient descent 

8 .Bellman Equation Value function can be unrolled recursively Q π (s, a) = E rt+1 + γrt+2 + γ 2 rt+3 + ... | s, a = Es r + γQ π (s , a ) | s, a Optimal value function Q ∗ (s, a) can be unrolled recursively Q ∗ (s, a) = Es r + γ max Q ∗ (s , a ) | s, a a Value iteration algorithms solve the Bellman equation Qi+1 (s, a) = Es r + γ max Qi (s , a ) | s, a a 

9 .Deep Q-Learning Represent value function by deep Q-network with weights w Q(s, a, w ) ≈ Q π (s, a) Define objective function by mean-squared error in Q-values  2     L(w ) = E  r + γ max  Q(s , a , w ) − Q(s, a, w )  a   target Leading to the following Q-learning gradient ∂L(w ) ∂Q(s, a, w ) =E r + γ max Q(s , a , w ) − Q(s, a, w ) ∂w a ∂w ∂L(w ) Optimise objective end-to-end by SGD, using ∂w 

10 .Stability Issues with Deep RL Naive Q-learning oscillates or diverges with neural nets 1. Data is sequential Successive samples are correlated, non-iid 2. Policy changes rapidly with slight changes to Q-values Policy may oscillate Distribution of data can swing from one extreme to another 3. Scale of rewards and Q-values is unknown Naive Q-learning gradients can be large unstable when backpropagated 

11 .Deep Q-Networks DQN provides a stable solution to deep value-based RL 1. Use experience replay Break correlations in data, bring us back to iid setting Learn from all past policies 2. Freeze target Q-network Avoid oscillations Break correlations between Q-network and target 3. Clip rewards or normalize network adaptively to sensible range Robust gradients 

12 .Stable Deep RL (1): Experience Replay To remove correlations, build data-set from agent’s own experience Take action at according to -greedy policy Store transition (st , at , rt+1 , st+1 ) in replay memory D Sample random mini-batch of transitions (s, a, r , s ) from D Optimise MSE between Q-network and Q-learning targets, e.g. 2 L(w ) = Es,a,r ,s ∼D r + γ max Q(s , a , w ) − Q(s, a, w ) a 

13 .Stable Deep RL (2): Fixed Target Q-Network To avoid oscillations, fix parameters used in Q-learning target Compute Q-learning targets w.r.t. old, fixed parameters w − r + γ max Q(s , a , w − ) a Optimise MSE between Q-network and Q-learning targets 2 L(w ) = Es,a,r ,s ∼D r + γ max Q(s , a , w − ) − Q(s, a, w ) a Periodically update fixed parameters w − ← w 

14 .Stable Deep RL (3): Reward/Value Range DQN clips the rewards to [−1, +1] This prevents Q-values from becoming too large Ensures gradients are well-conditioned Can’t tell difference between small and large rewards 

15 .Reinforcement Learning in Atari state action st at reward rt 

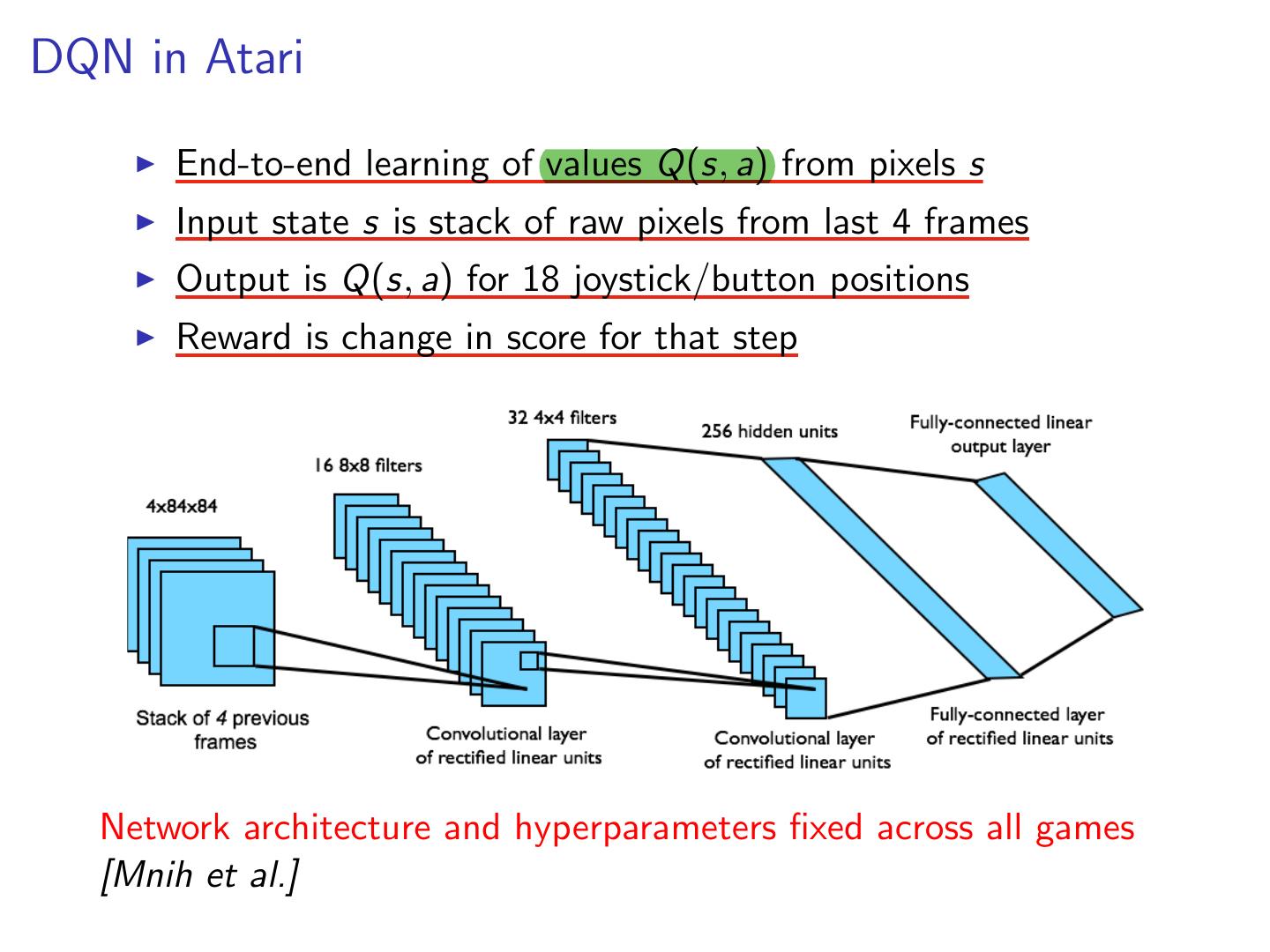
16 .DQN in Atari End-to-end learning of values Q(s, a) from pixels s Input state s is stack of raw pixels from last 4 frames Output is Q(s, a) for 18 joystick/button positions Reward is change in score for that step Network architecture and hyperparameters fixed across all games [Mnih et al.] 

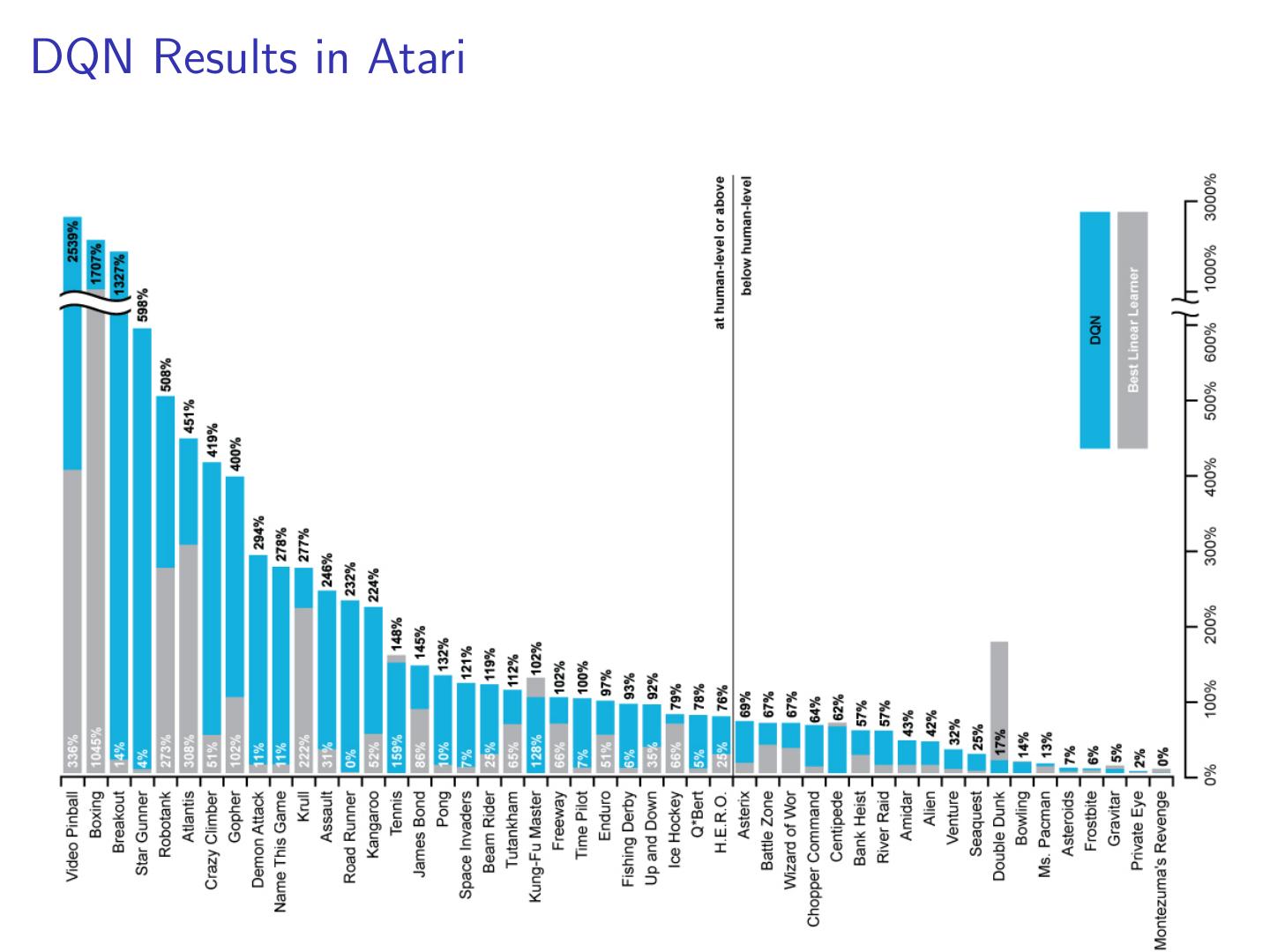
17 .DQN Results in Atari 

18 .DQN Demo 

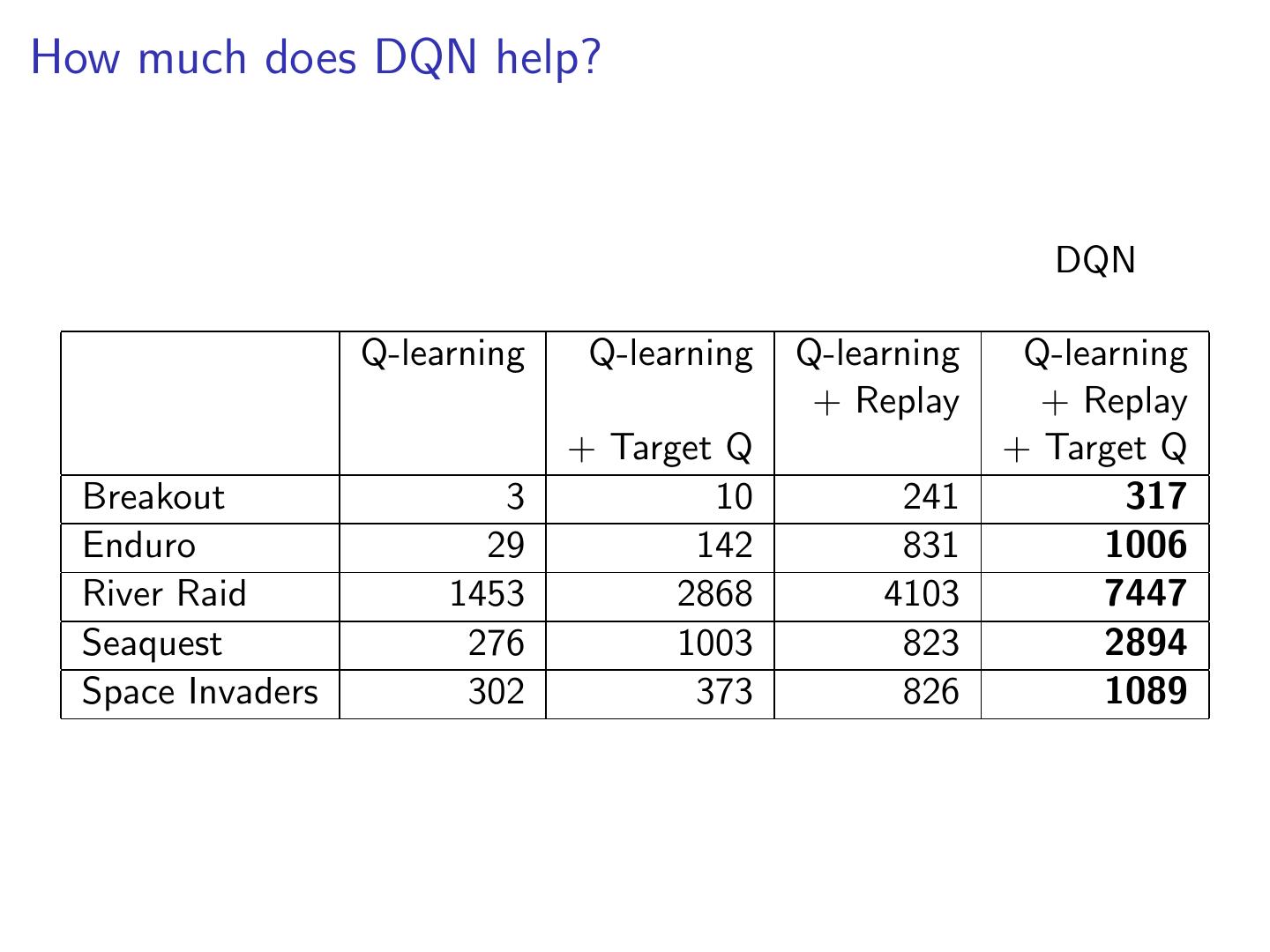
19 .How much does DQN help? DQN Q-learning Q-learning Q-learning Q-learning + Replay + Replay + Target Q + Target Q Breakout 3 10 241 317 Enduro 29 142 831 1006 River Raid 1453 2868 4103 7447 Seaquest 276 1003 823 2894 Space Invaders 302 373 826 1089 

20 .Normalized DQN Normalized DQN uses true (unclipped) reward signal Network outputs a scalar value in “stable” range, U(s, a, w ) ∈ [−1, +1] Output is scaled and translated into Q-values, Q(s, a, w , σ, π) = σU(s, a, w ) + π π, σ are adapted to ensure U(s, a, w ) ∈ [−1, +1] Network parameters w are adjusted to keep Q-values constant σ1 U(s, a, w1 ) + π1 = σ2 U(s, a, w2 ) + π2 

21 .Demo: Normalized DQN in PacMan 

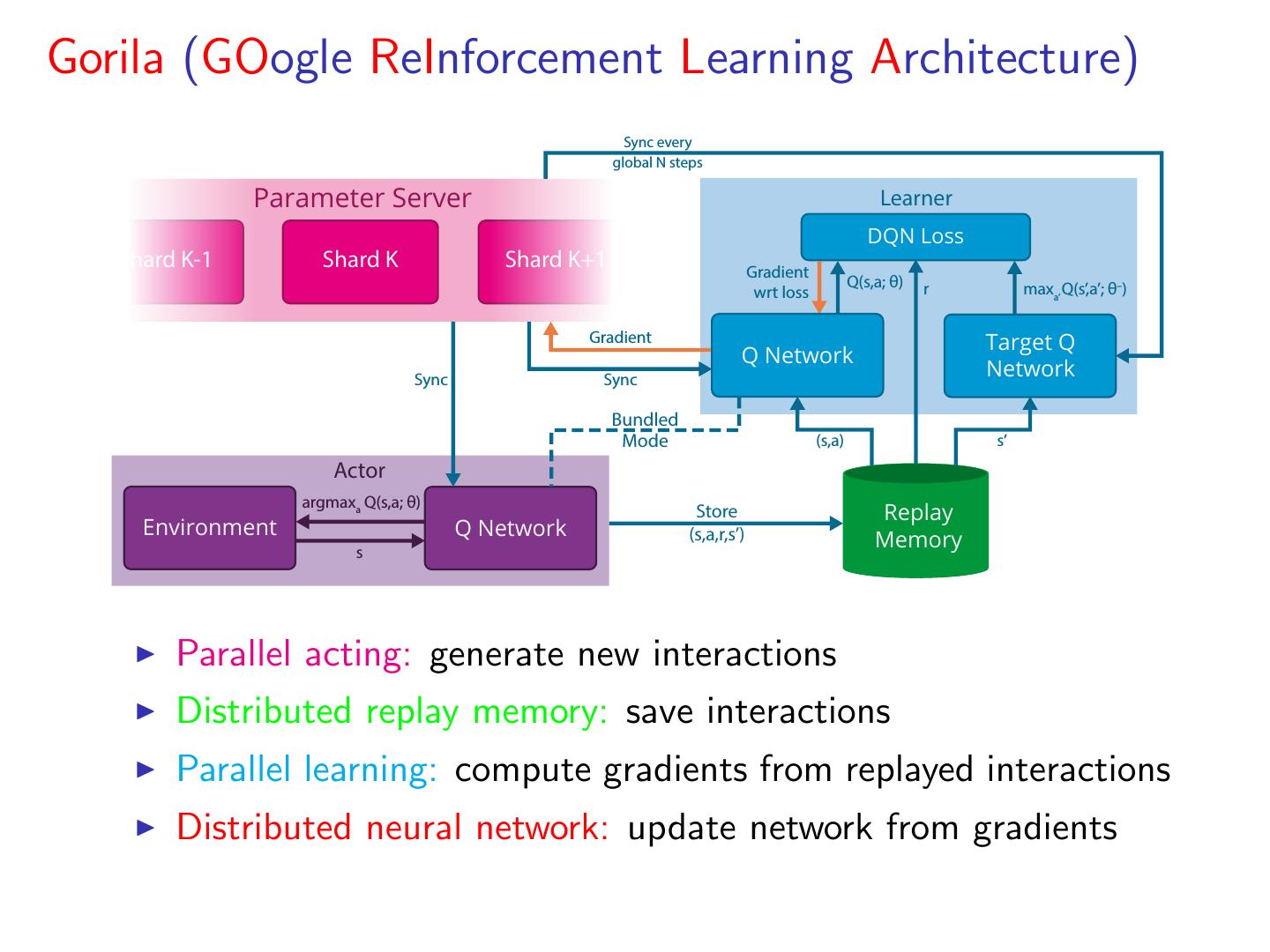
22 .Gorila (GOogle ReInforcement Learning Architecture) Sync every global N steps Parameter Server Learner DQN Loss Shard K-1 Shard K Shard K+1 Gradient Q(s,a; θ) r maxa’ Q(s’,a’; θ–) wrt loss Gradient Target Q Q Network Sync Sync Network Bundled Mode (s,a) s’ Actor argmaxa Q(s,a; θ) Store Replay Environment Q Network (s,a,r,s’) s Memory Parallel acting: generate new interactions Distributed replay memory: save interactions Parallel learning: compute gradients from replayed interactions Distributed neural network: update network from gradients 

23 .Stable Deep RL (4): Parallel Updates Vanilla DQN is unstable when applied in parallel. We use: Reject stale gradients Reject outlier gradients g > µ + kσ AdaGrad optimisation 

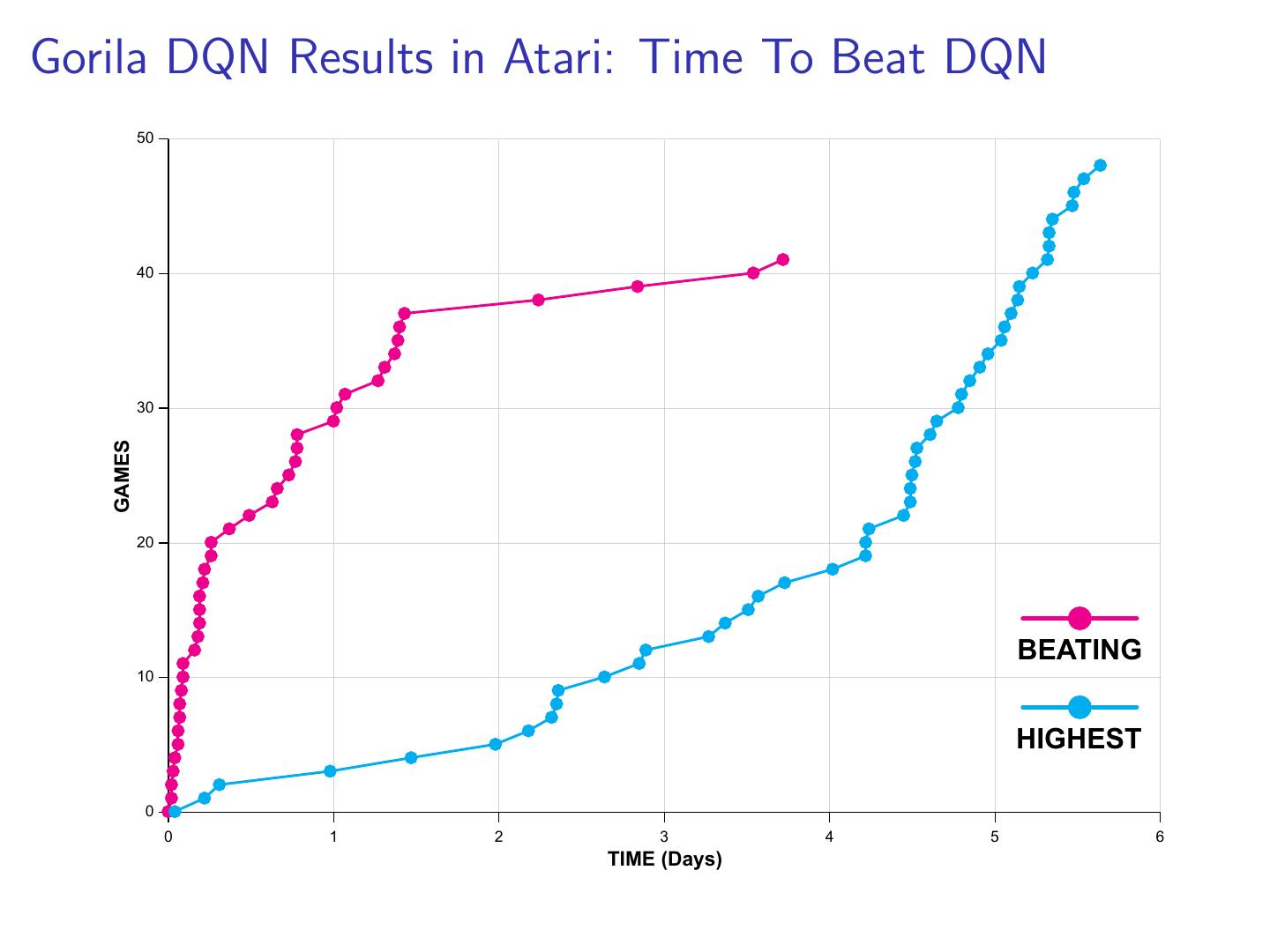
24 .Gorila Results Using 100 parallel actors and learners Gorila significantly outperformed Vanilla DQN on 41 out of 49 Atari games Gorila achieved x2 score of Vanilla DQN on 22 out of 49 Atari games Gorila matched Vanilla DQN results 10x faster on 38 out of 49 Atari games 

25 .Gorila DQN Results in Atari: Time To Beat DQN 50 40 30 GAMES 20 BEATING 10 HIGHEST 0 0 1 2 3 4 5 6 TIME (Days) 

26 .Deterministic Policy Gradient for Continuous Actions Represent deterministic policy by deep network a = π(s, u) with weights u Define objective function as total discounted reward J(u) = E r1 + γr2 + γ 2 r3 + ... Optimise objective end-to-end by SGD ∂J(u) ∂Q π (s, a) ∂π(s, u) = Es ∂u ∂a ∂u Update policy in the direction that most improves Q i.e. Backpropagate critic through actor 

27 .Deterministic Actor-Critic Use two networks: an actor and a critic Critic estimates value of current policy by Q-learning ∂L(w ) ∂Q(s, a, w ) =E r + γQ(s , π(s ), w ) − Q(s, a, w ) ∂w ∂w Actor updates policy in direction that improves Q ∂J(u) ∂Q(s, a, w ) ∂π(s, u) = Es ∂u ∂a ∂u 

28 .Deterministic Deep Actor-Critic Naive actor-critic oscillates or diverges with neural nets DDAC provides a stable solution 1. Use experience replay for both actor and critic 2. Use target Q-network to avoid oscillations ∂L(w ) ∂Q(s, a, w ) = Es,a,r ,s ∼D r + γQ(s , π(s ), w − ) − Q(s, a, w ) ∂w ∂w ∂J(u) ∂Q(s, a, w ) ∂π(s, u) = Es,a,r ,s ∼D ∂u ∂a ∂u 

29 .DDAC for Continuous Control End-to-end learning of control policy from raw pixels s Input state s is stack of raw pixels from last 4 frames Two separate convnets are used for Q and π Physics are simulated in MuJoCo a Q(s,a) π(s) [Lillicrap et al.]