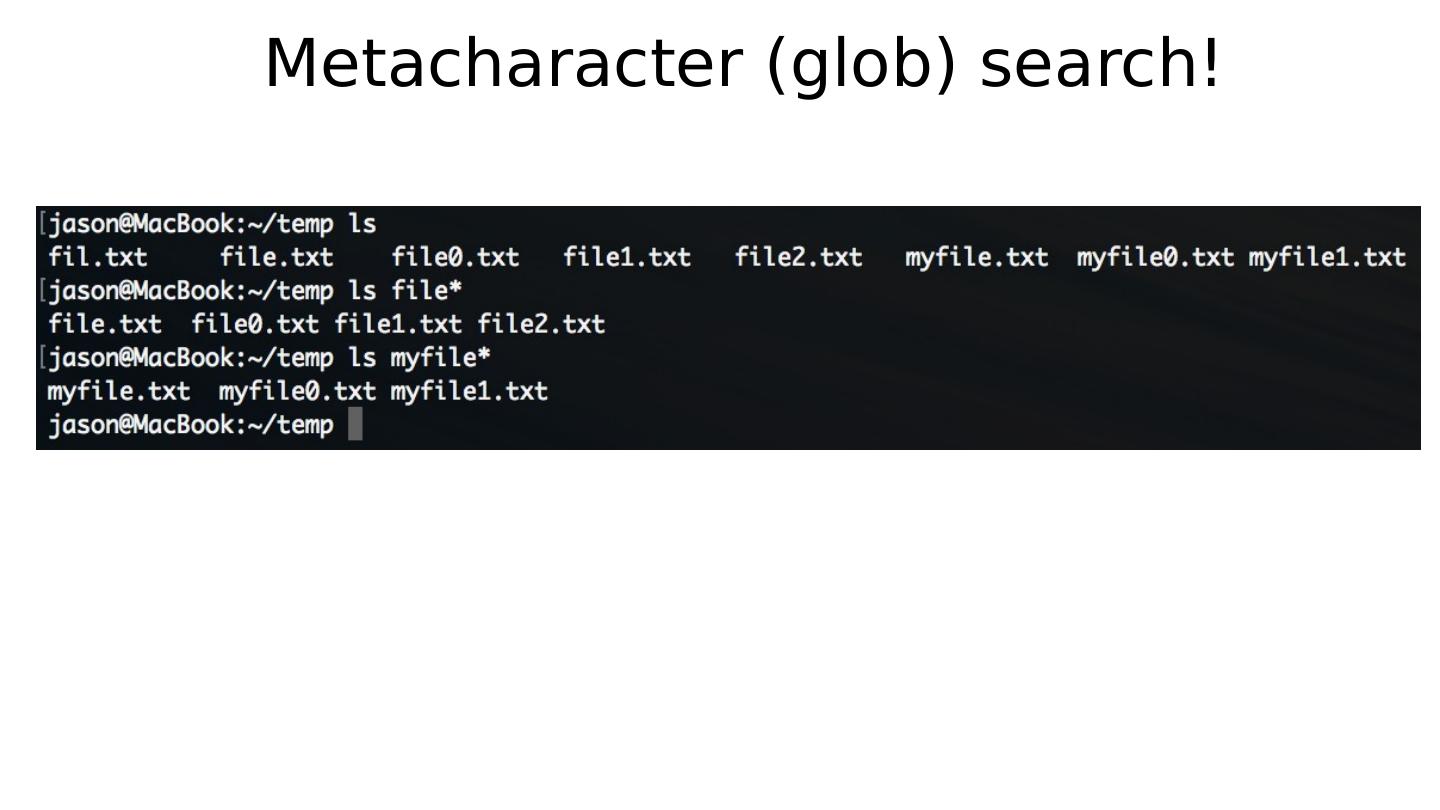
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Tries树
展开查看详情
1 .Tries CMSC 420
2 .A brief history of character sets 1963: A merican S tandard C ode for I nformation I nterchange ( ASCII ) Used numbers from 32 through 127 to encode unaccented English characters and some common symbols, like >, <, _, etc The numbers from 0 through 31 were used for control characters that are not all particularly useful nowadays, like BELL, printer feed, etc. Need only 7 bits to encode those, so with 1 extra bit, you can do whatever you want! Example: the IBM-PC, which was using an Intel 8088 CPU used a standard known as OEM …
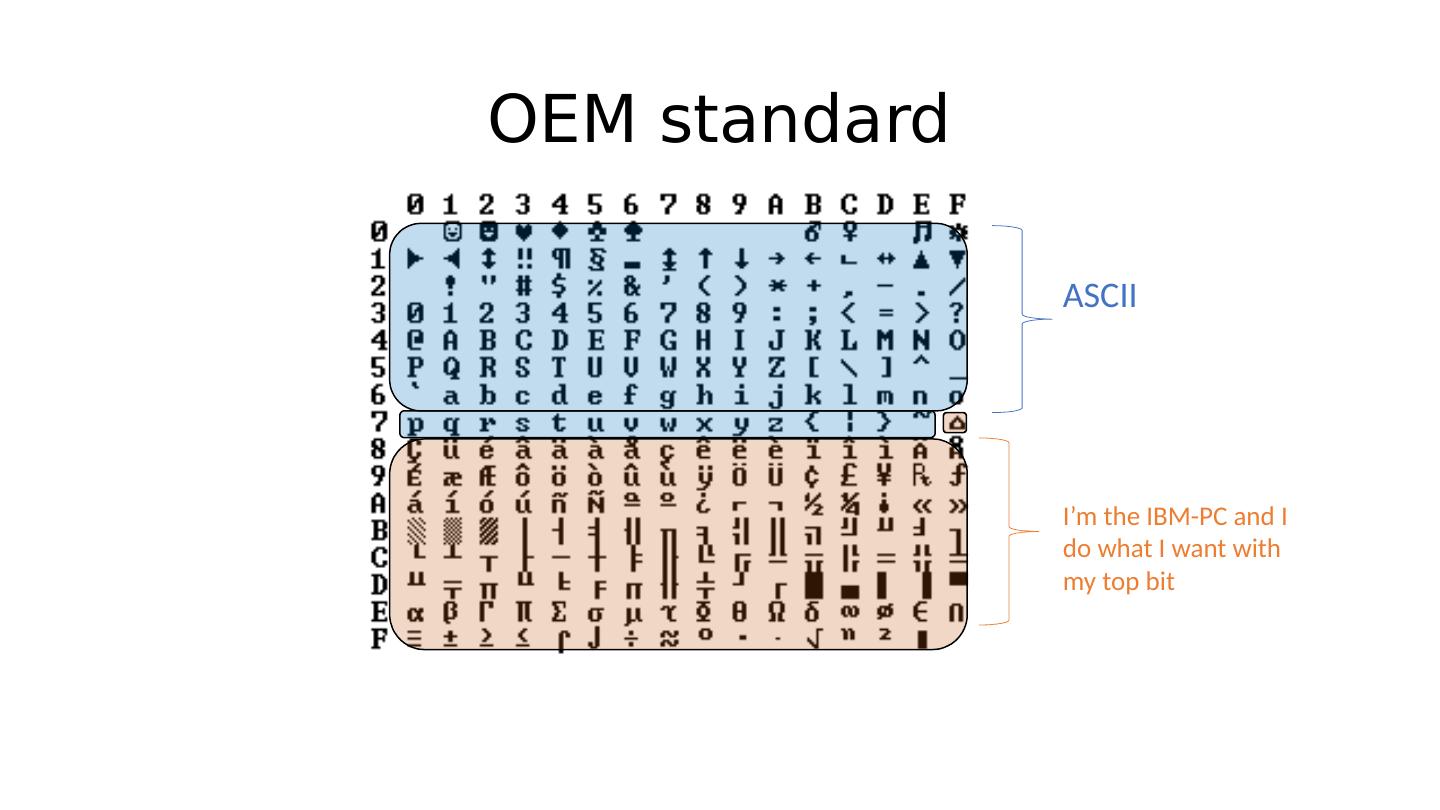
3 .OEM standard
4 .OEM standard Last ASCII character, since 127 (10) = 0x7E
5 .OEM standard ASCII I’m the IBM-PC and I do what I want with my top bit
6 .ASCII I’m the IBM-PC and I do what I want with my top bit OEM standard Some whitespace character at 0x20 = 32 (10)
7 .OEM standard ASCII Space character at 0x20 = 32 (10) Capital ‘N’ at 0x5E = 95 (10) I’m the IBM-PC and I do what I want with my top bit
8 .OEM standard ASCII Space character at 0x20 = 32 (10) Capital ‘N’ at 0x5E = 95 (10) Unsurprisingly, this turned out to be a problem… Main reason: Speakers of radically different languages could be using the IBM-PC, and they needed to use that eighth bit differently! I’m the IBM-PC and I do what I want with my top bit
9 .ANSI Solution: Code pages Axiom: Everybody agrees on the ASCII subset So, 7 LSBs interpretable in only one way across all computers in the world. Top bit: Alphabet-specific This led to different code pages for different alphabets ! E.g Icelandic: Code page #00861, Greek: Code page CP00851 So, as long as all Greek computers use ANSI CP00851 (reasonable assumption), they will all be able to transmit strings to one another without problems
10 .Problems with code page scheme Advent of the web and e-mail: browsers and mail programs would need to store all code books in order to be able to decode messages from different countries correctly ! Back in the day, when memory was expensive , this required a lot of space. E.g Jason wants to use his Mac, manufactured in China, according to American specifications, to e-mail his mother, who is currently in China, using a laptop purchased in Greece. Oh, and he types the e-mail in Greek! For some languages, e.g Mandarin, 8 bits are simply not enough !
11 .The Unicode standard Defined and maintained by the Unicode Consortium . An effort to develop a “mega-code page” to satisfy all users in the world. Every character gets mapped to a single “ code point” which is just a number in Hex followed by the string “U+” (stands for Unicode) . E.g U+03 88 = (Greek lowercase lambda), U+ 0153= œ ( latin ‘ oe ’) “ H e ll o ” = U+0048 U+0065 U+006C U+006C U+006F . This hex number does not necessarily represent the number of bits required to store the character in memory! E.g U+10FFFF is the largest Unicode codepoint and clearly it can not fit into either one or two bytes… How the code point itself is mapped to memory (the code point’s encoding ) is left to the destination computer
12 .Implementation of encodings STEP 0: EVERYBODY AGREES ON USING UNICODE. EVERYONE. Step 1: Select an encoding. Many different encodings of Unicode exist , and are pre-installed in all major OSs. UCS2 and its successor UTF-16 stores the codepoint U+xxxx using exactly xxxx , so in 16 bits. UTF8 stores every codepoint in MULTIPLES OF 1 BYTE . (variable-length encoding) Codepoints from U+0x0000 to U+0x7E (127 (10) ) are stored within an entire byte of their own (so the MSB is effectively ignored !). Codepoints above 127 (10) use as many bytes as they might need! Step 2: The sender needs to tell the recipient what kind of Unicode encoding it used to build the text E-mail headers are a good example In HTML, we can use <meta> tags
13 .UTF-8 is kind of bigoted Or is it? Vast majority of pairs of receivers – senders in the world will send and read characters in English (so, from the set of the first 128 characters that UTF-8 represents in a single byte) This is exactly ASCII ! As a result, the vast majority of messages can be encoded in one byte per character. We can’t hope to do any better when encoding a single character ! Non-English speakers or people who want to use rare characters are disadvantaged : additional storage cost has to be paid ! Experimentation : try to load a webpage in Mandarin, making sure that the HTML source reads <meta http- equiv =“utf8” right after the <html> tag … It should take longer than loading the Washington Post , for instance.
14 .ASCII is good enough for us! For our study of strings, 128 characters will be enough . So we limit ourselves to ASCII (technically, 7 of the 8 bits contained in the byte reserved via our assumed UTF-8 encoding). ‘A’ in ASCII: 0x41 = 65 (10) ‘a’ in ASCII: 0x61 = 97 (10) Since 65 + 24 = 89 < 97, some characters in between lowercase and uppercase alphabet… Subtracting 65 from all of our code points allows us to treat ‘A’ at 0… In most of our examples, we will be giving an example alphabet, so this entire discussion only applicable to real-world tries .
15 .Tries Pronounced exactly like the verb ! E.g “José tries to catch the ball” This can be sometimes perplexing, since they are essentially trees … don’t let this confuse you. A trie is a tree-like data structure where nodes store the entire alphabet , and branches are taken based on the relevant character of the string that is searched for (or inserted / deleted). An additional bit field tells us if we have reached an actual string that was stored in the trie . Invented in late 1950s by René de la Briandais , esteemed French person.
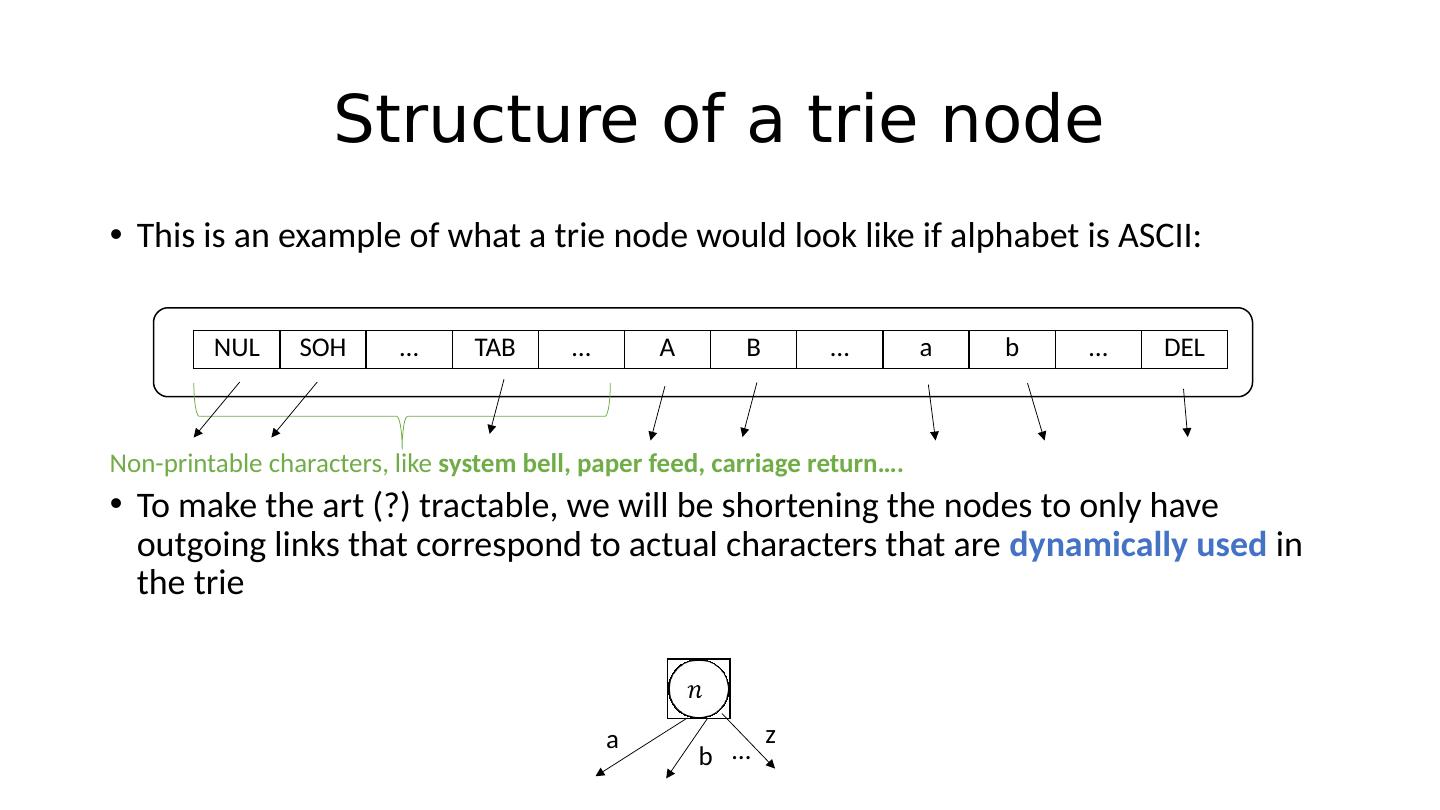
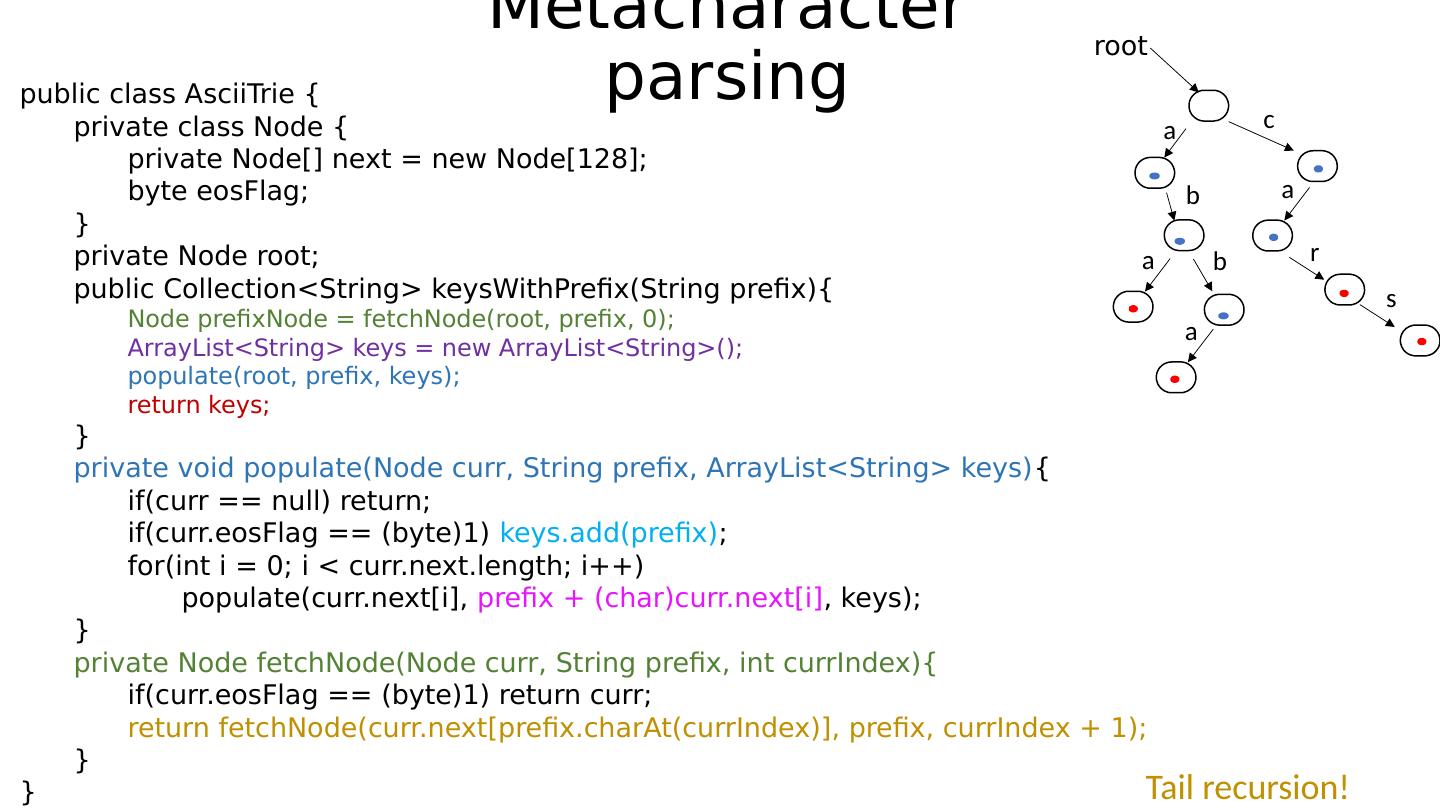
16 .Structure of a trie node We must always specify the alphabet that we sample characters from! Common choices: ASCII, UNICODE. In this course, we will be using ASCII or small subsets thereof. Every node will hold a buffer with many cells! Question: For UNICODE ( usable symbols) , how big will those buffers be in bytes ?
17 .Structure of a trie node We must always specify the alphabet that we sample characters from! Common choices: ASCII, UNICODE. In this course, we will be using ASCII or small subsets thereof. Every node will hold a buffer with many cells! Question: For UNICODE ( usable symbols) , how big will those buffers be in bytes ? 128 65K >65K <65K
18 .Structure of a trie node We must always specify the alphabet that we sample characters from! Common choices: ASCII, UNICODE. In this course, we will be using ASCII or small subsets thereof. Every node will hold a buffer with many cells! Question: For UNICODE ( usable symbols) , how big will those buffers be in bytes ? 128 65K >65K <65K Only the first 128 characters are stored in a single byte each!
19 .Structure of a trie node This is an example of what a trie node would look like if alphabet is ASCII: To make the art (?) tractable, we will be shortening the nodes to only have outgoing links that correspond to actual characters that are dynamically used in the trie NUL SOH … TAB … A B … a b … DEL Non-printable characters, like system bell, paper feed, carriage return … . a b z …
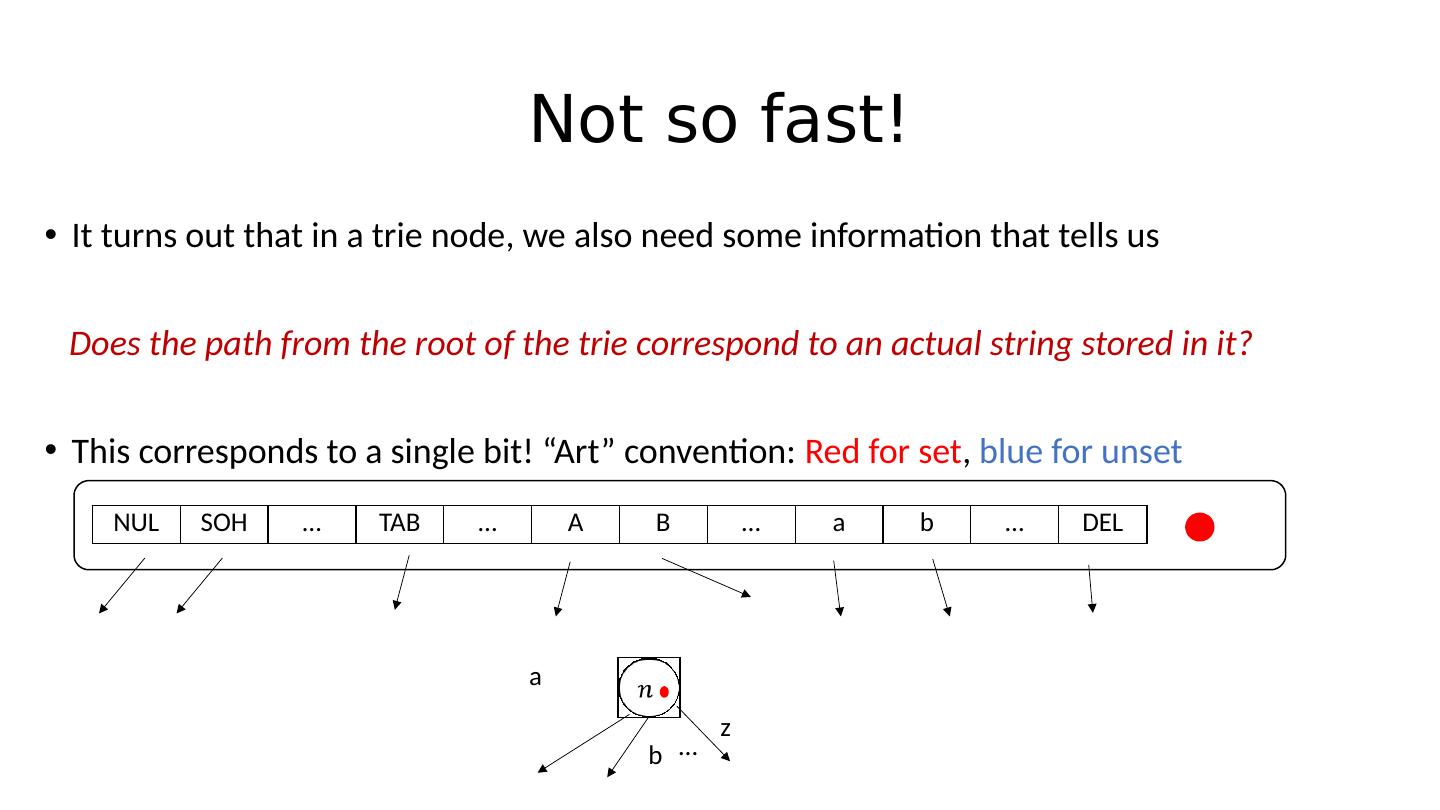
20 .Not so fast! It turns out that in a trie node, we also need some information that tells us Does the path from the root of the trie correspond to an actual string stored in it? This corresponds to a single bit! “Art” convention: Red for set , blue for unset NUL SOH … TAB … A B … a b … DEL a b z …
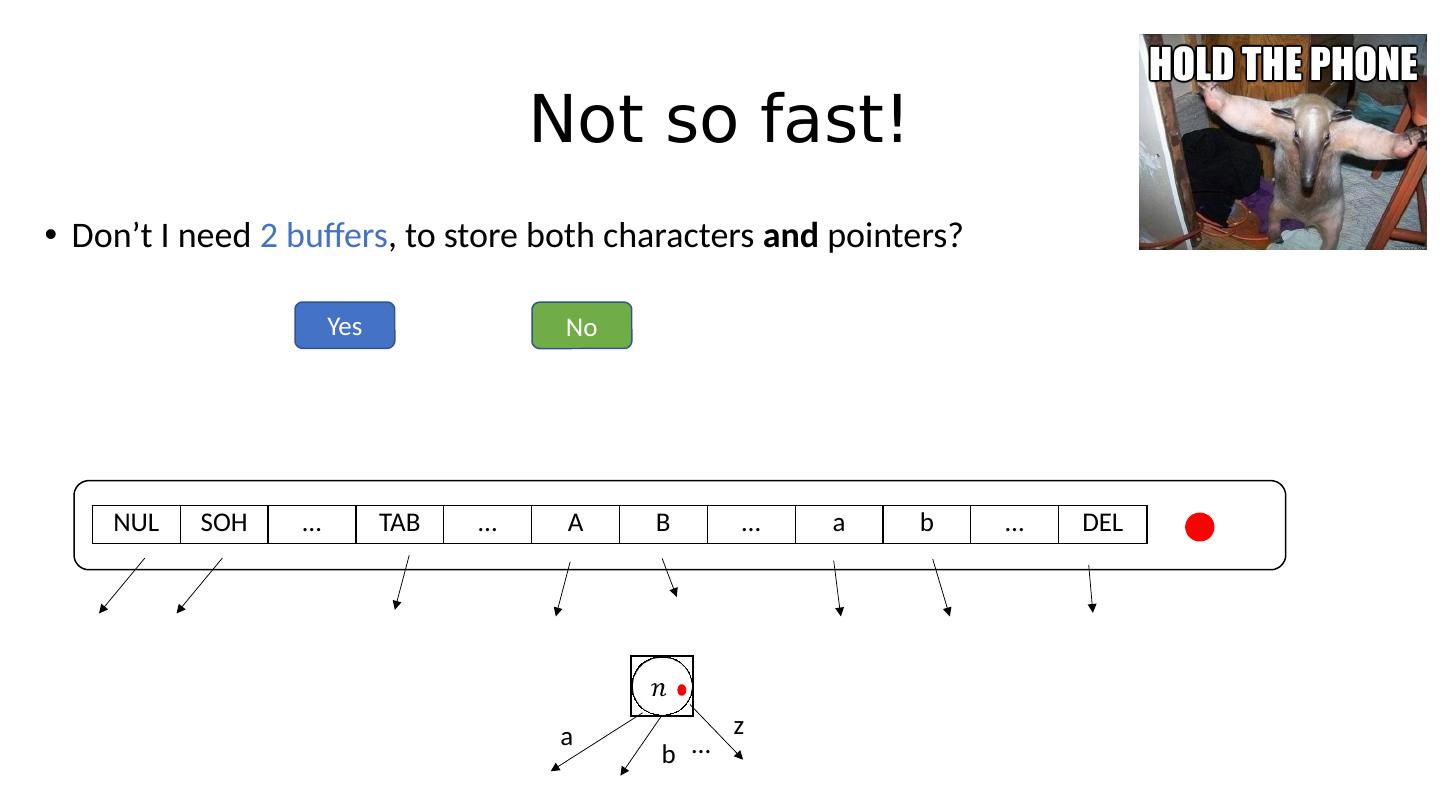
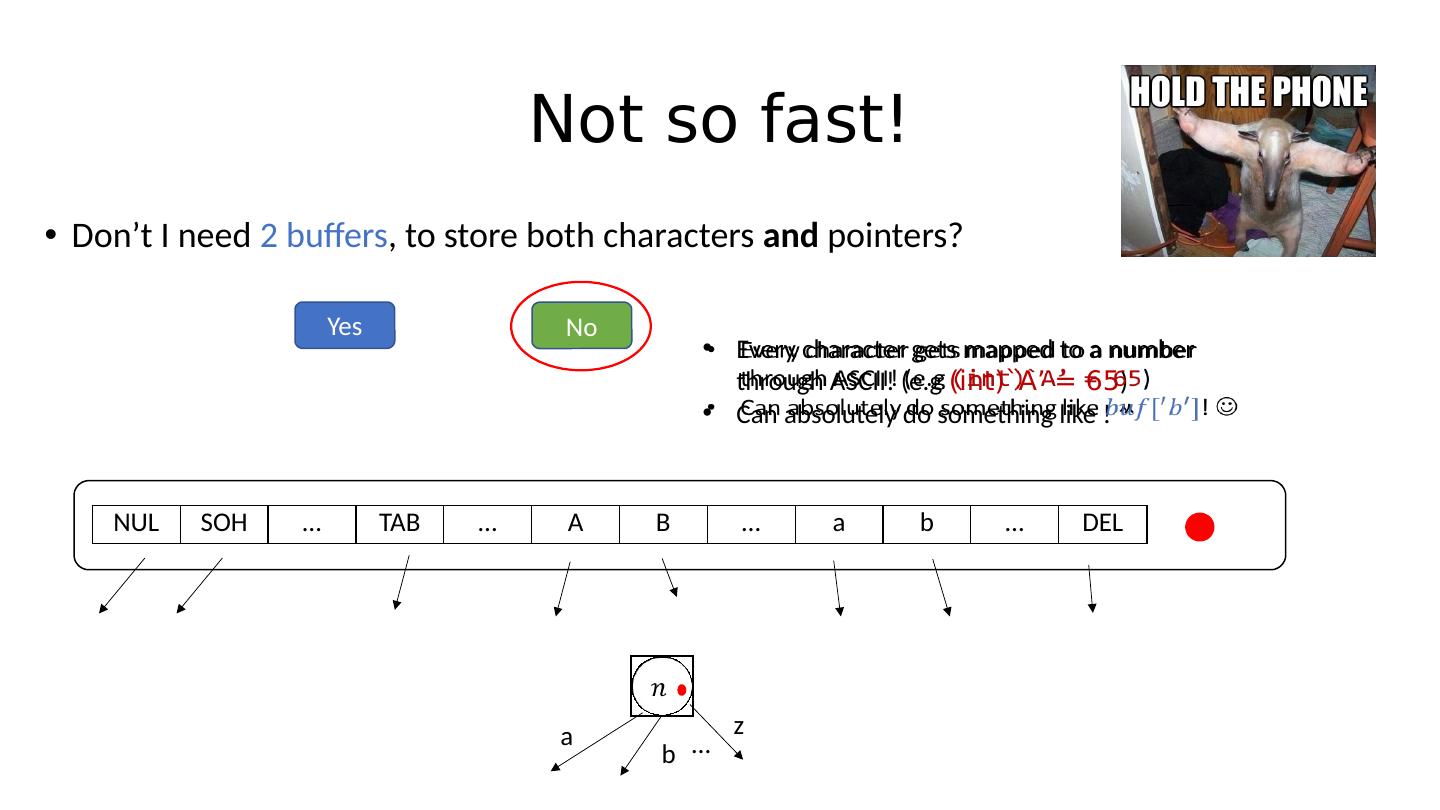
21 .Not so fast! Don’t I need 2 buffers , to store both characters and pointers? NUL SOH … TAB … A B … a b … DEL a b z …
22 .Not so fast! Don’t I need 2 buffers , to store both characters and pointers? NUL SOH … TAB … A B … a b … DEL a b z … Yes No
23 .Not so fast! Don’t I need 2 buffers , to store both characters and pointers? NUL SOH … TAB … A B … a b … DEL a b z … Yes No Every character gets mapped to a number through ASCII! ( e.g ( int )`A’ = 65 ) Can absolutely do something like !
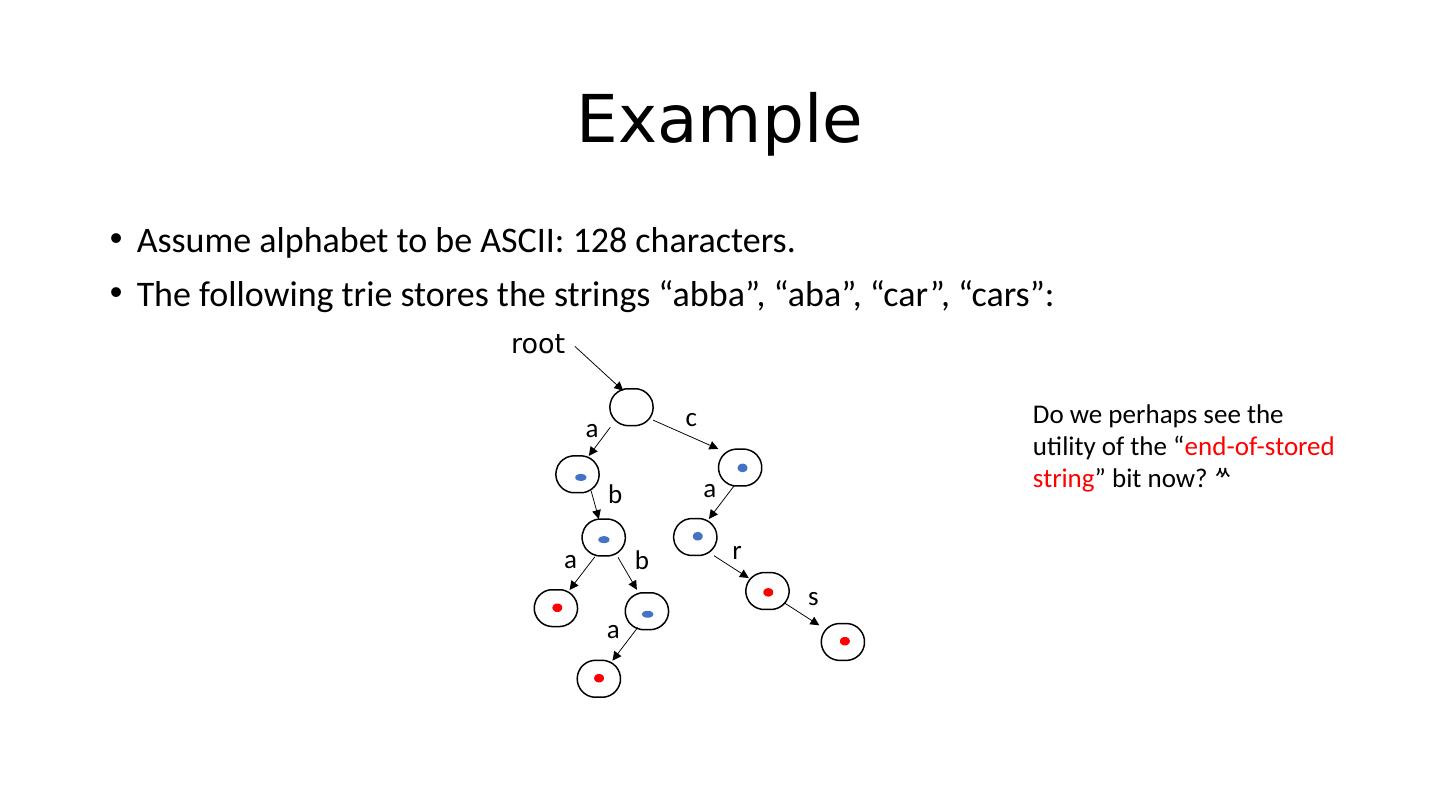
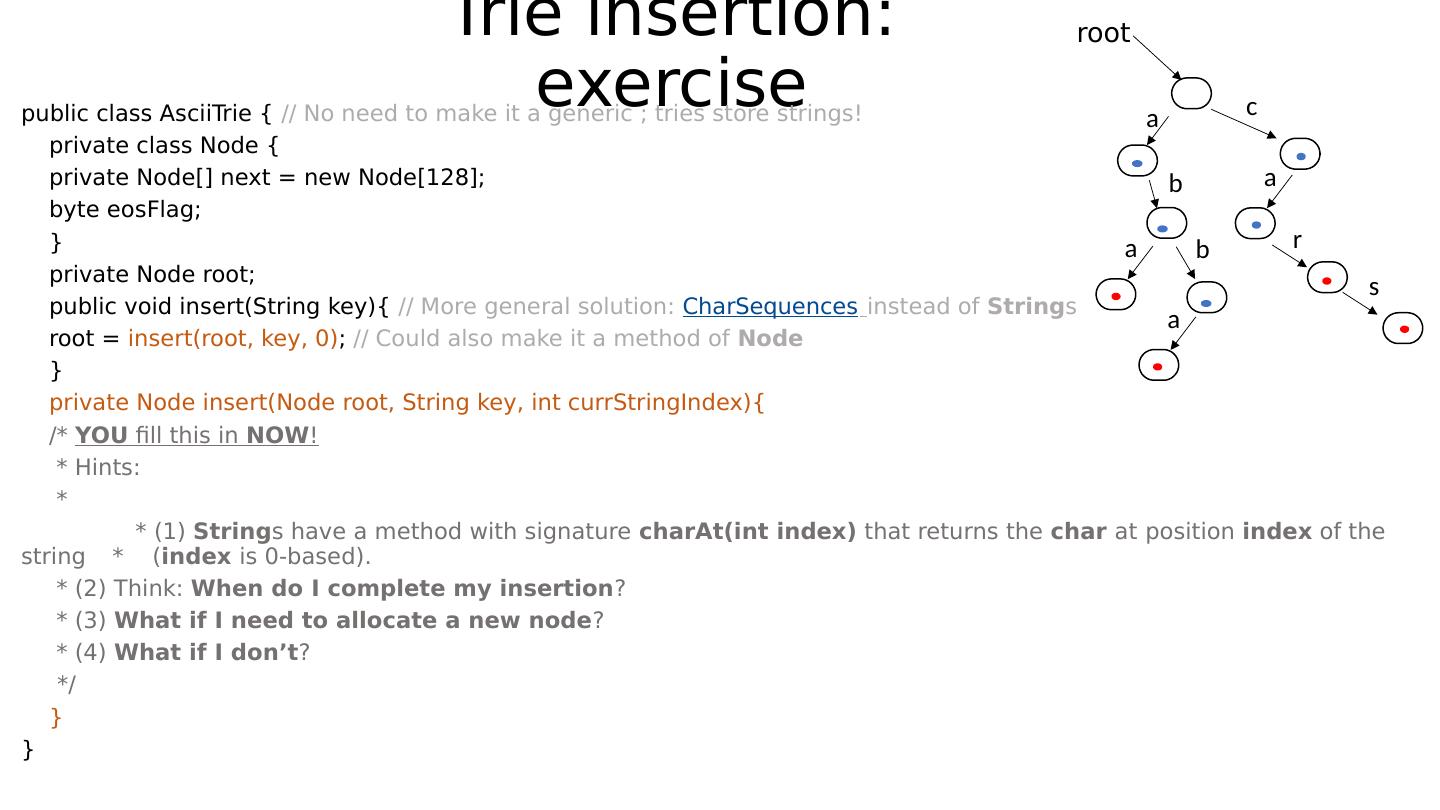
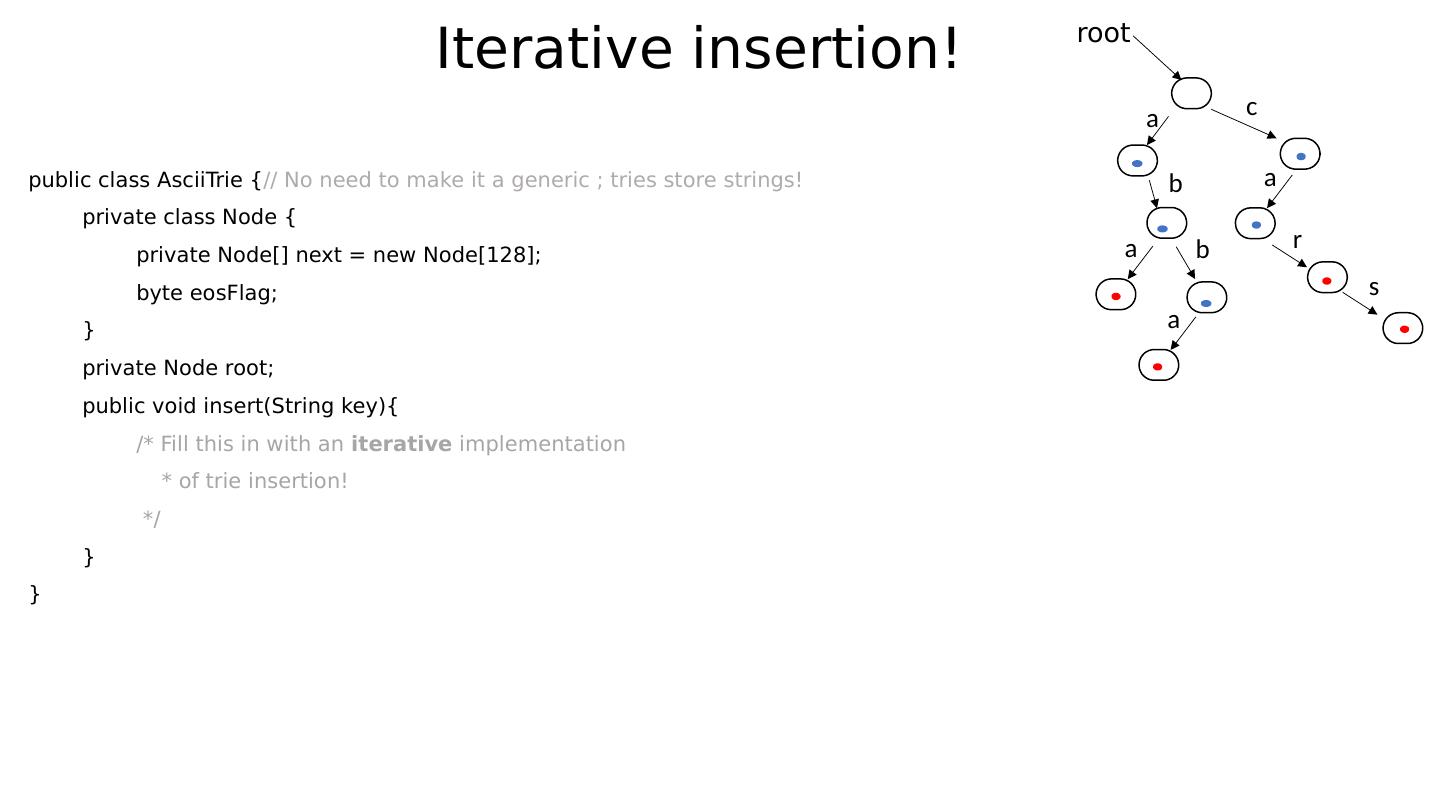
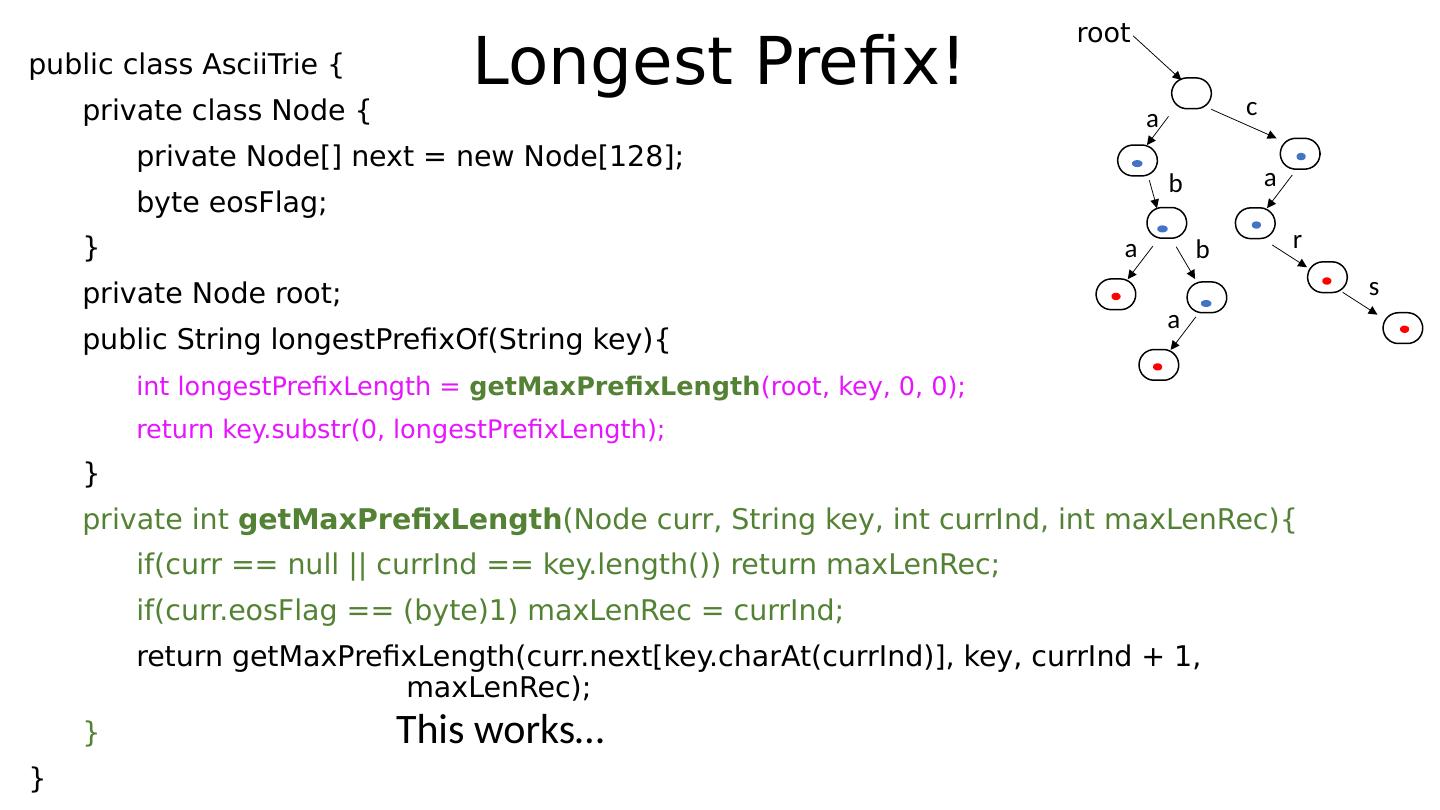
24 .Example Assume alphabet to be ASCII: 128 characters. The following trie stores the strings “ abba ”, “aba”, “car”, “cars”: root a b a b a c a r s
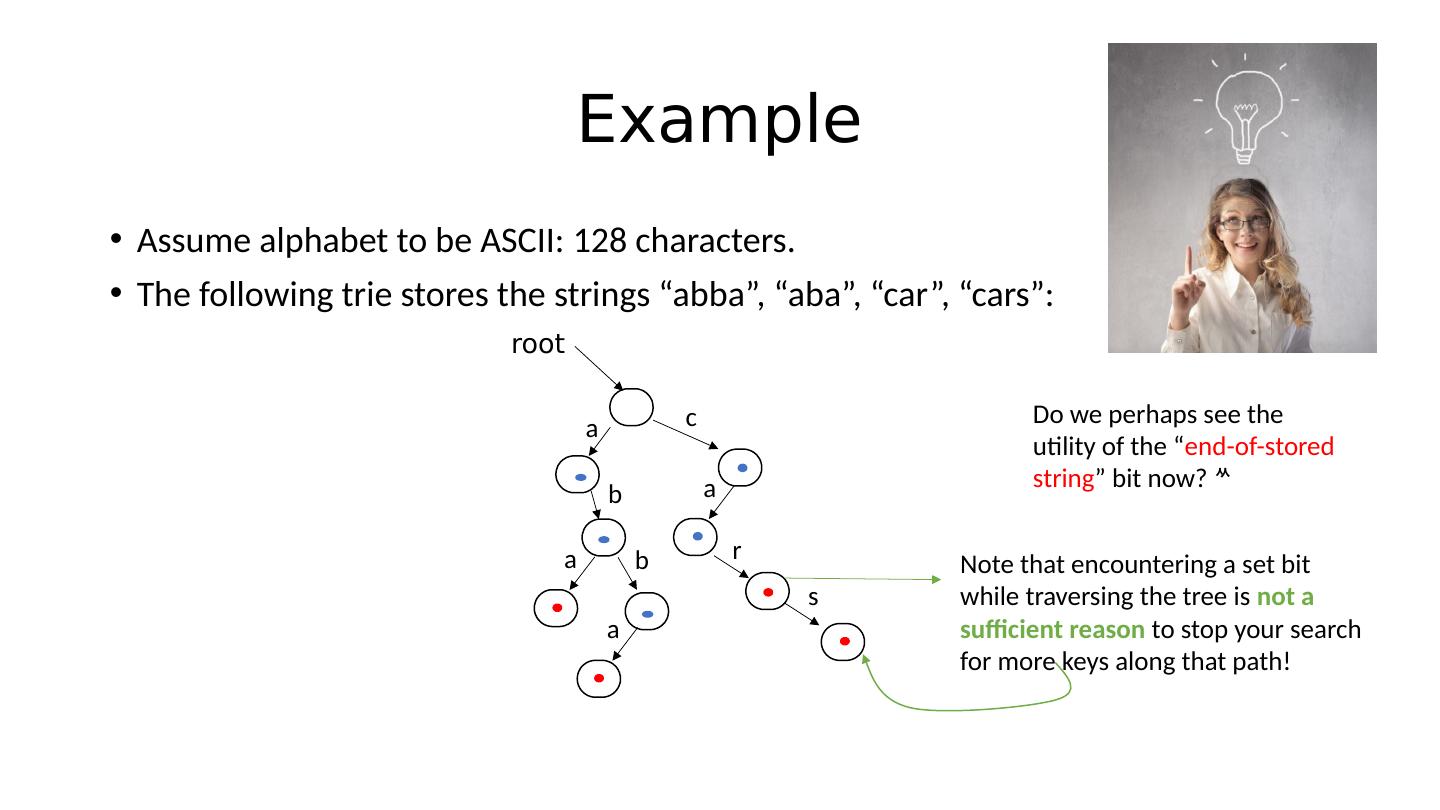
25 .Example Assume alphabet to be ASCII: 128 characters. The following trie stores the strings “ abba ”, “aba”, “car”, “cars”: root a b a b a c a r s Do we perhaps see the utility of the “ end-of-stored string ” bit now?
26 .Example Assume alphabet to be ASCII: 128 characters. The following trie stores the strings “ abba ”, “aba”, “car”, “cars”: root a b a b a c a r s Do we perhaps see the utility of the “ end-of-stored string ” bit now? Note that encountering a set bit while traversing the tree is not a sufficient reason to stop your search for more keys along that path!
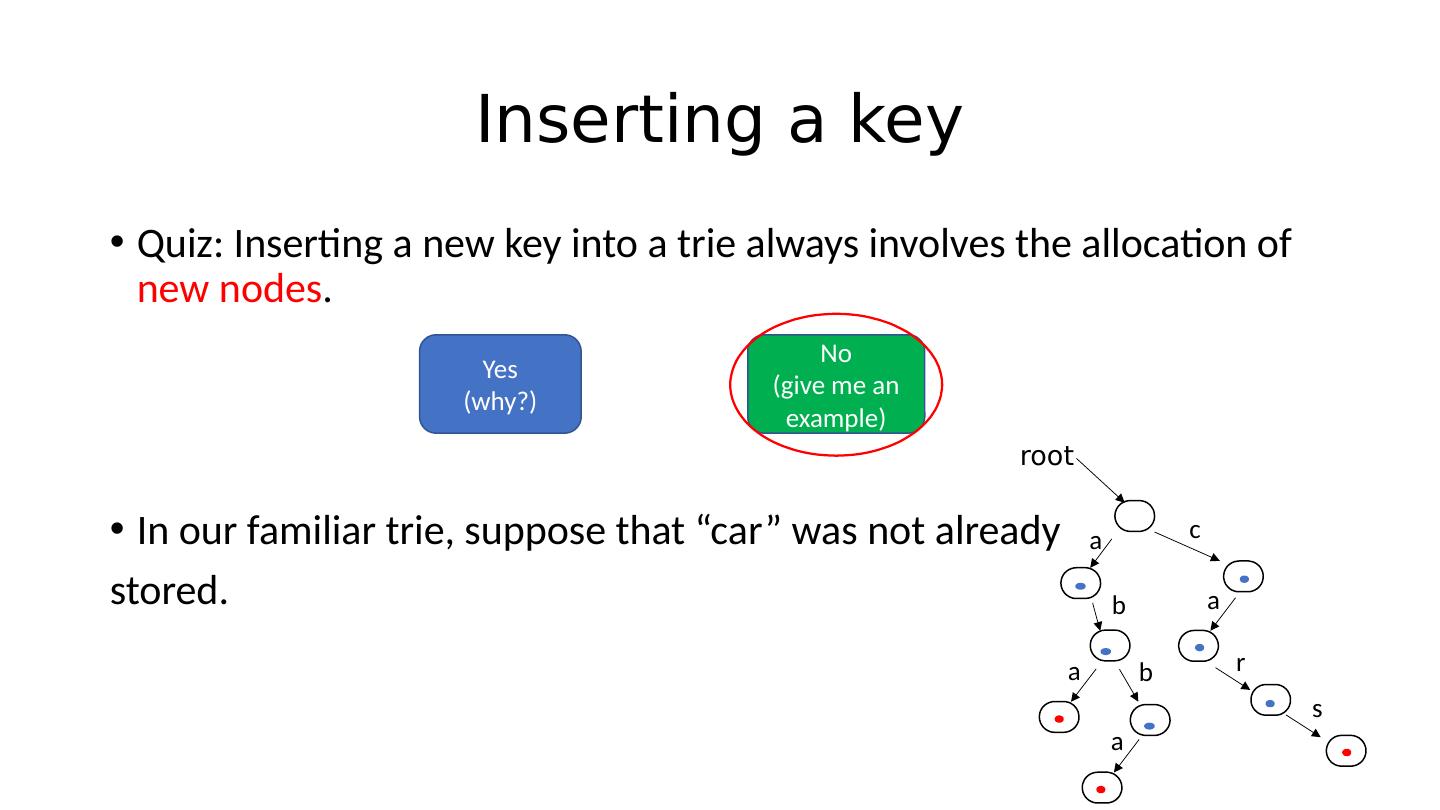
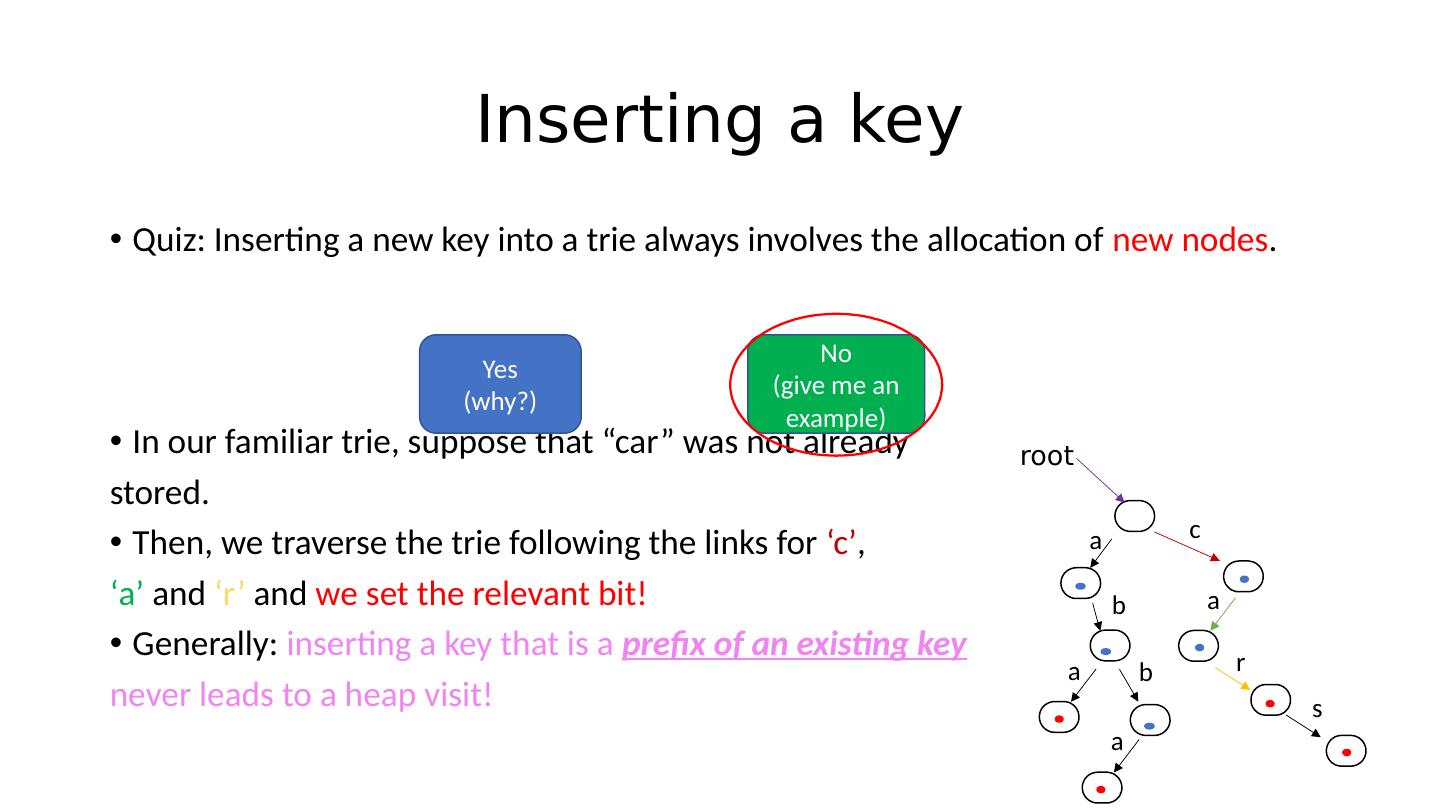
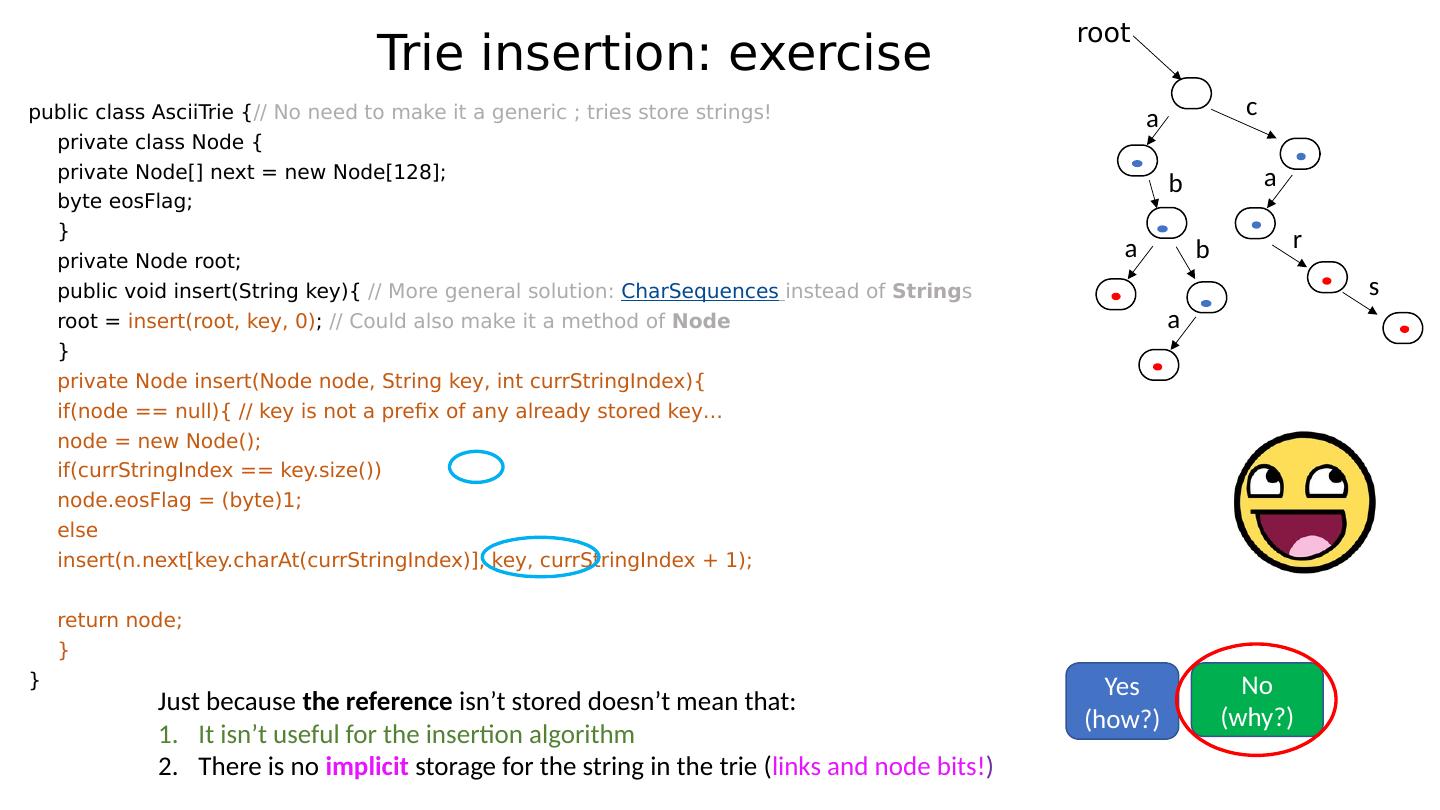
27 .Inserting a key Quiz: Inserting a new key into a trie always involves the allocation of new nodes . Yes (why?) No (give me an example)
28 .Inserting a key Quiz: Inserting a new key into a trie always involves the allocation of new nodes . In our familiar trie , suppose that “car” was not already stored. Yes (why?) No (give me an example) root a b a b a c a r s
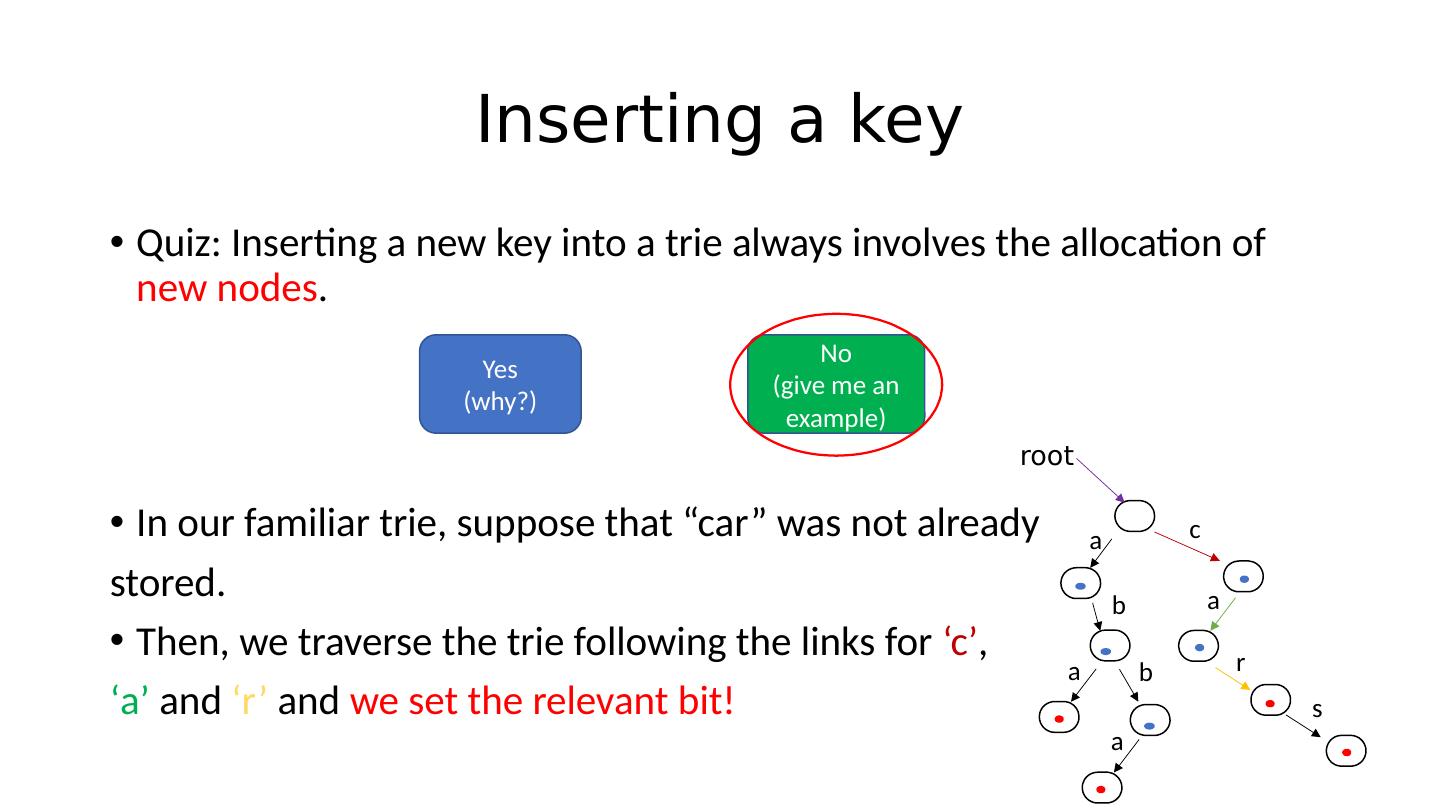
29 .Inserting a key Quiz: Inserting a new key into a trie always involves the allocation of new nodes . In our familiar trie , suppose that “car” was not already stored. Then, we traverse the trie following the links for ‘c’ , ‘a’ and ‘r’ and we set the relevant bit! Yes (why?) No (give me an example) root a b a b a c a r s