展开查看详情
1 .Intro to Deep Learning, TensorFlow,
and tensorflow.js
JavaScript Meetup 09/11/2018
Shape Security Mountain View
Oswald Campesato
ocampesato@yahoo.com
2 . Highlights/Overview
intro to AI/ML/DL/NNs
Hidden layers
Initialization values
Neurons per layer
Activation function
cost function
gradient descent
learning rate
Dropout rate
what are CNNs
TensorFlow/tensorflow.js
4 . Use Cases for Deep Learning
computer vision
speech recognition
image processing
bioinformatics
social network filtering
drug design
Recommendation systems
Bioinformatics
Mobile Advertising
Many others
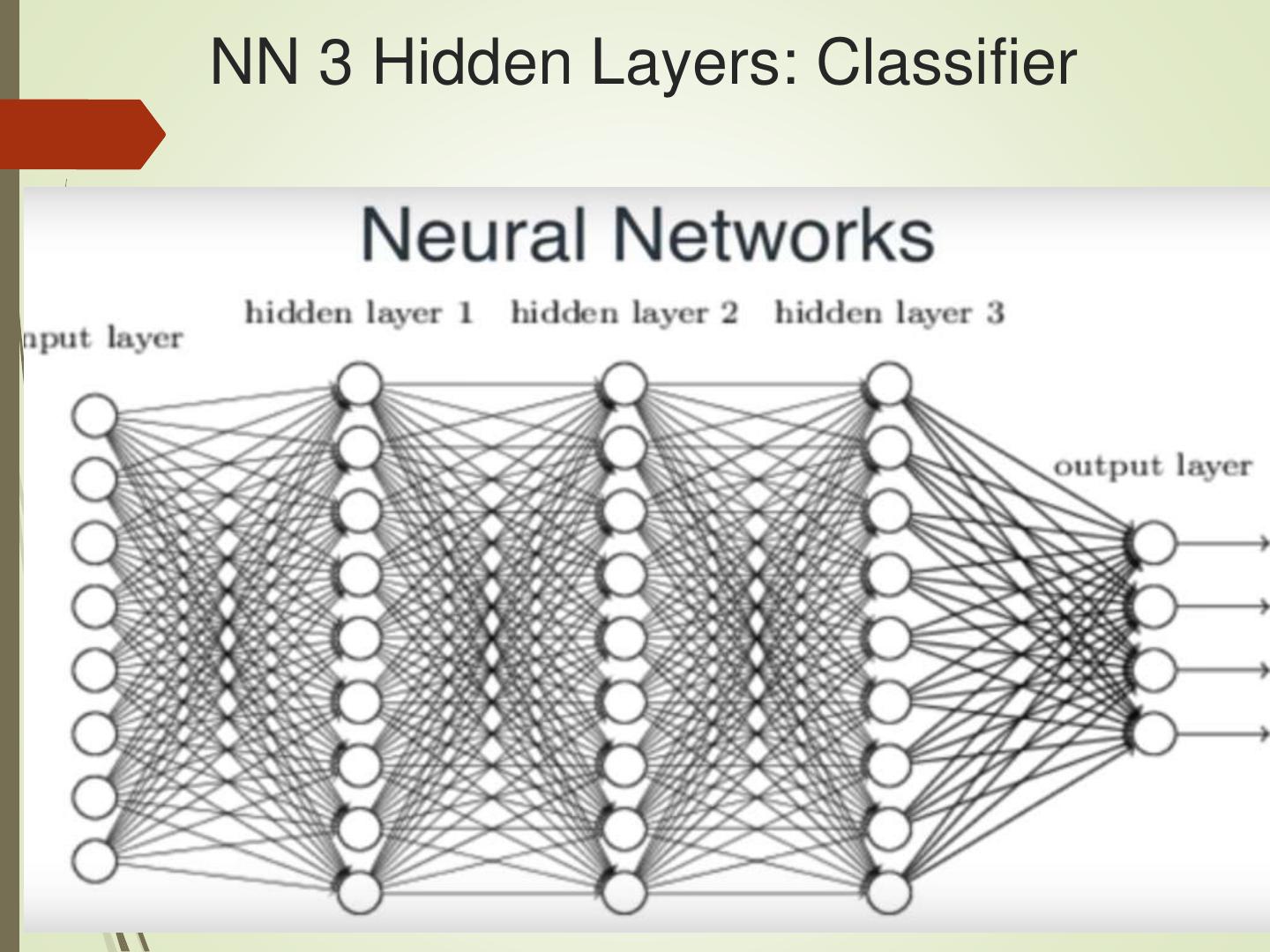
5 .NN 3 Hidden Layers: Classifier
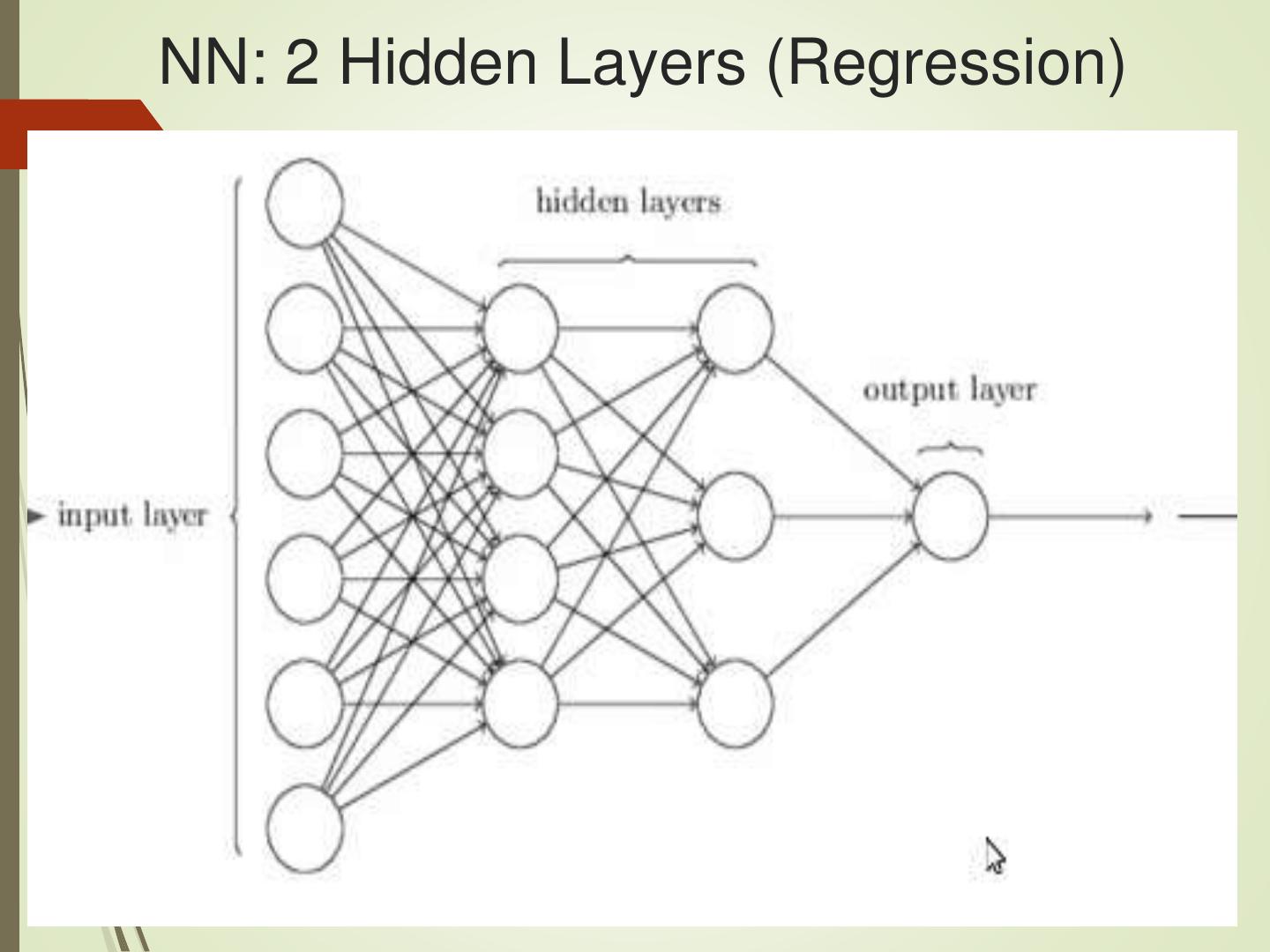
6 .NN: 2 Hidden Layers (Regression)
7 .Classification and Deep Learning
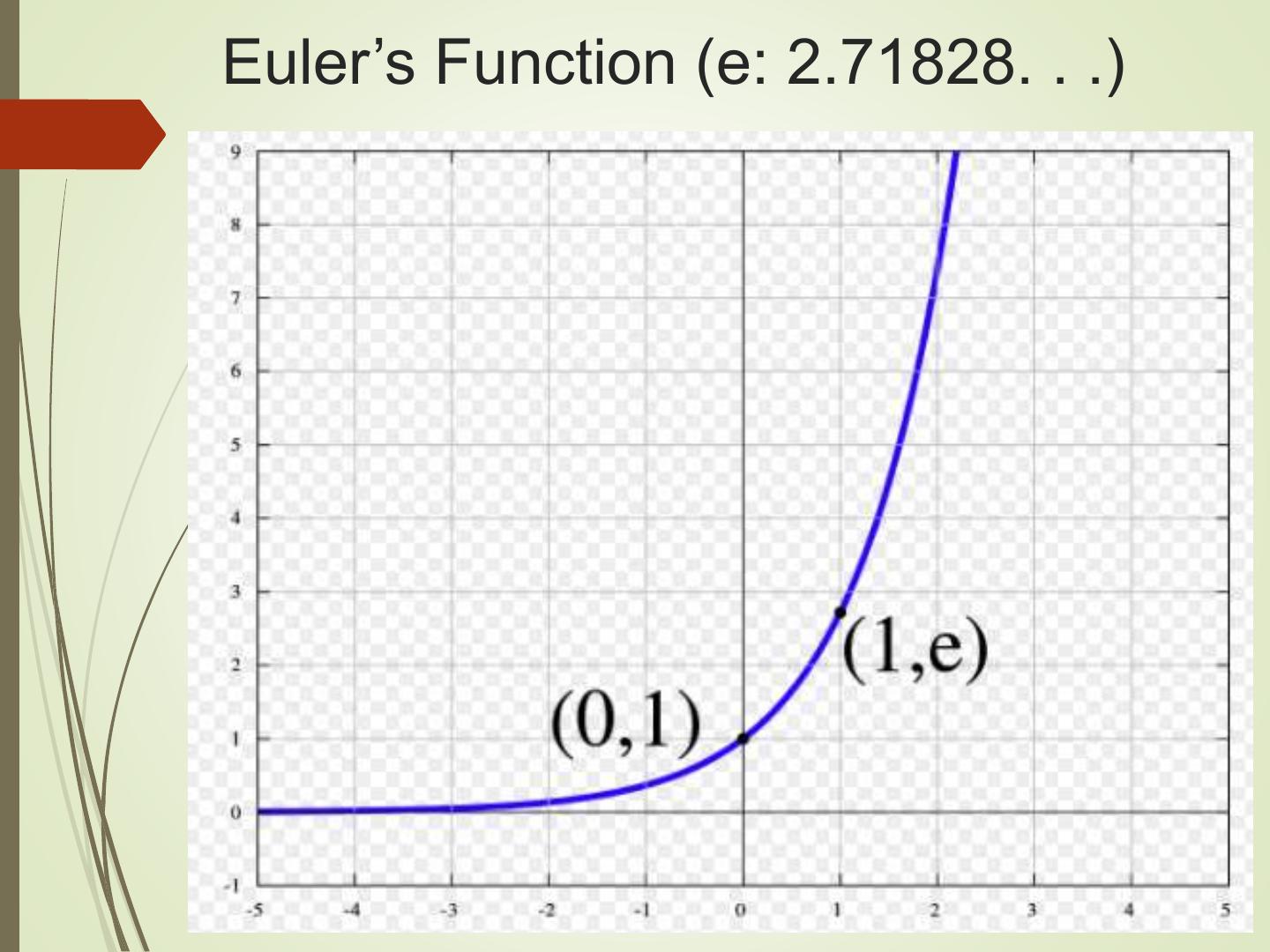
8 .Euler’s Function (e: 2.71828. . .)
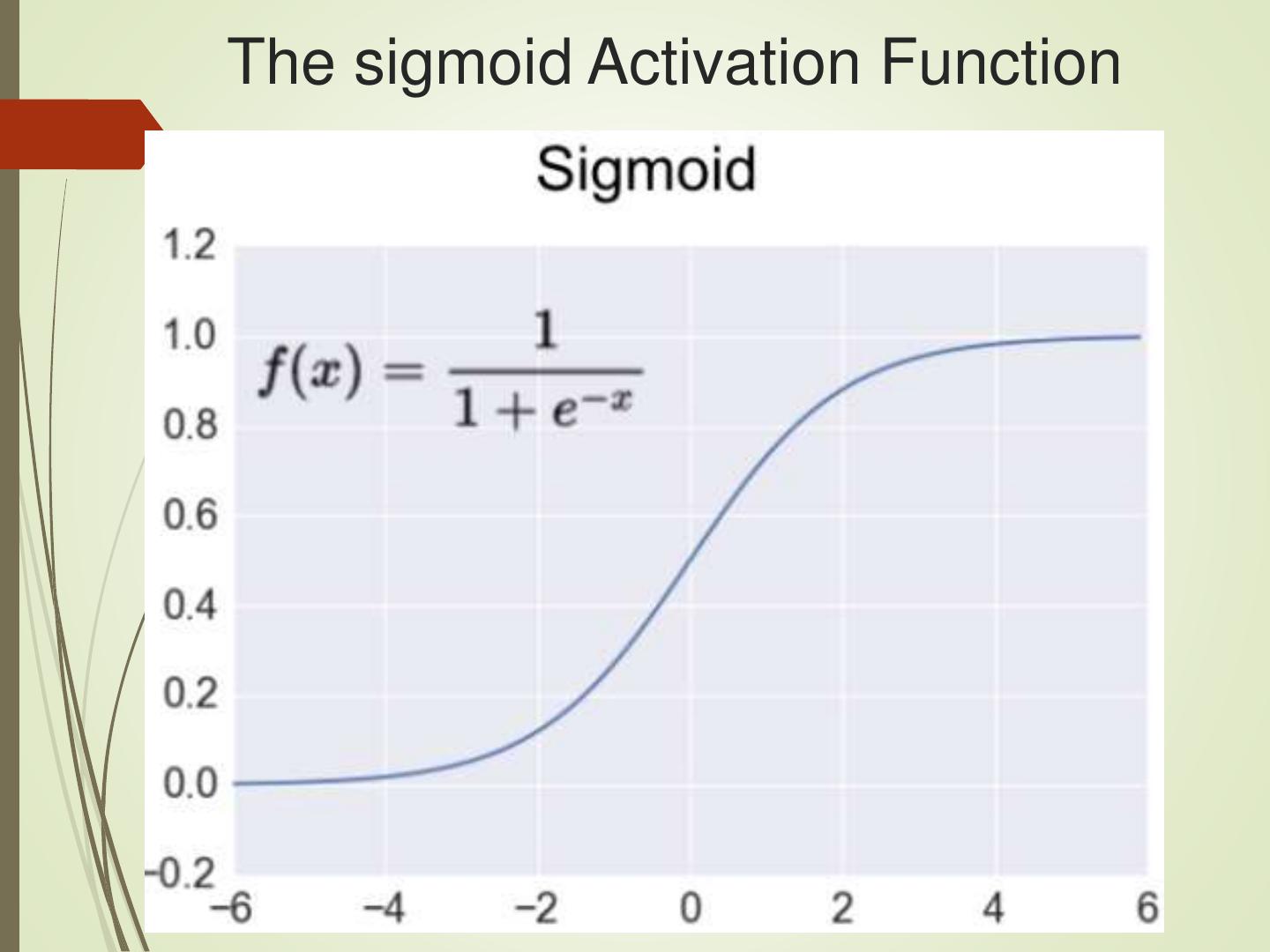
9 .The sigmoid Activation Function
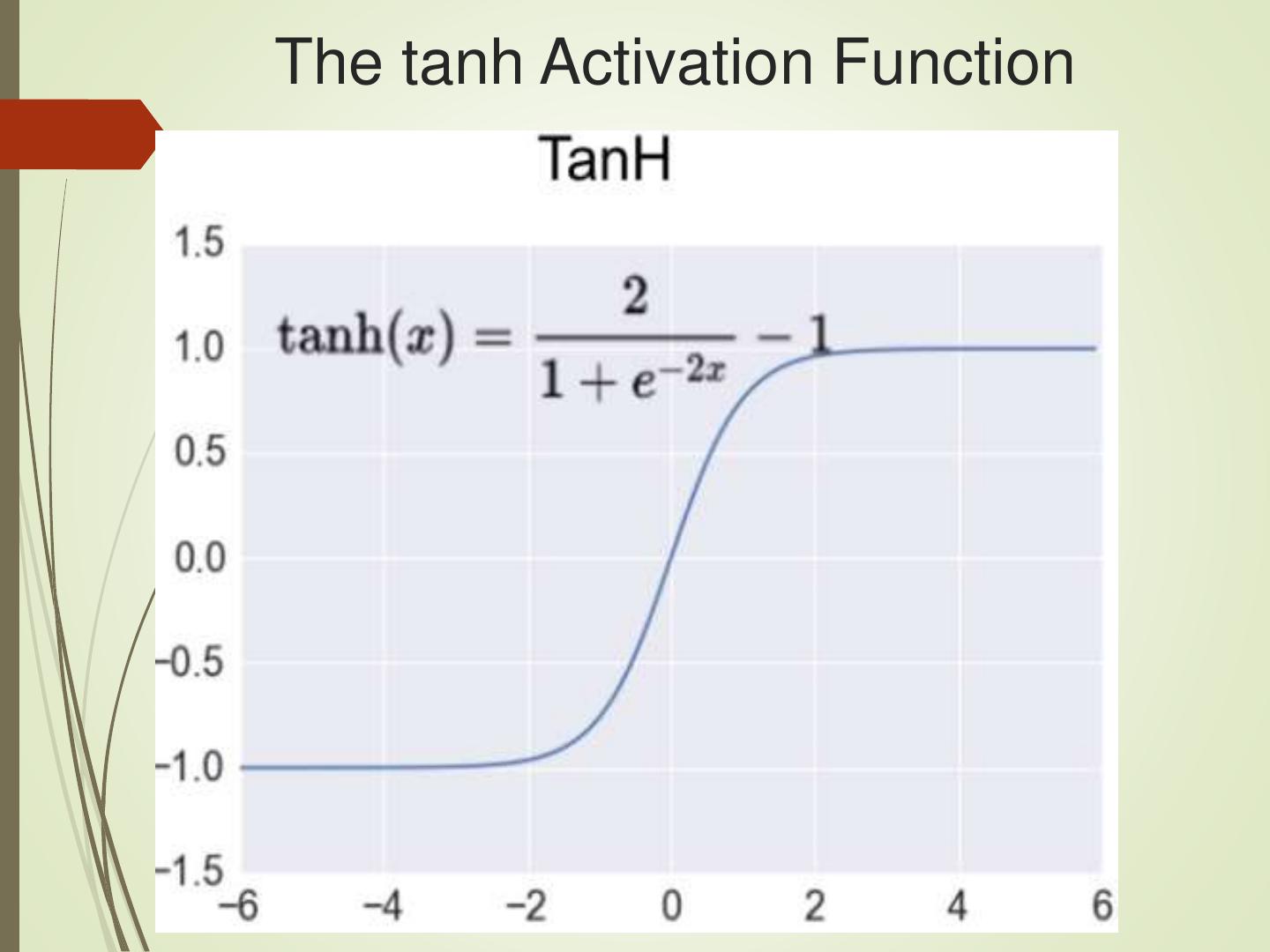
10 .The tanh Activation Function
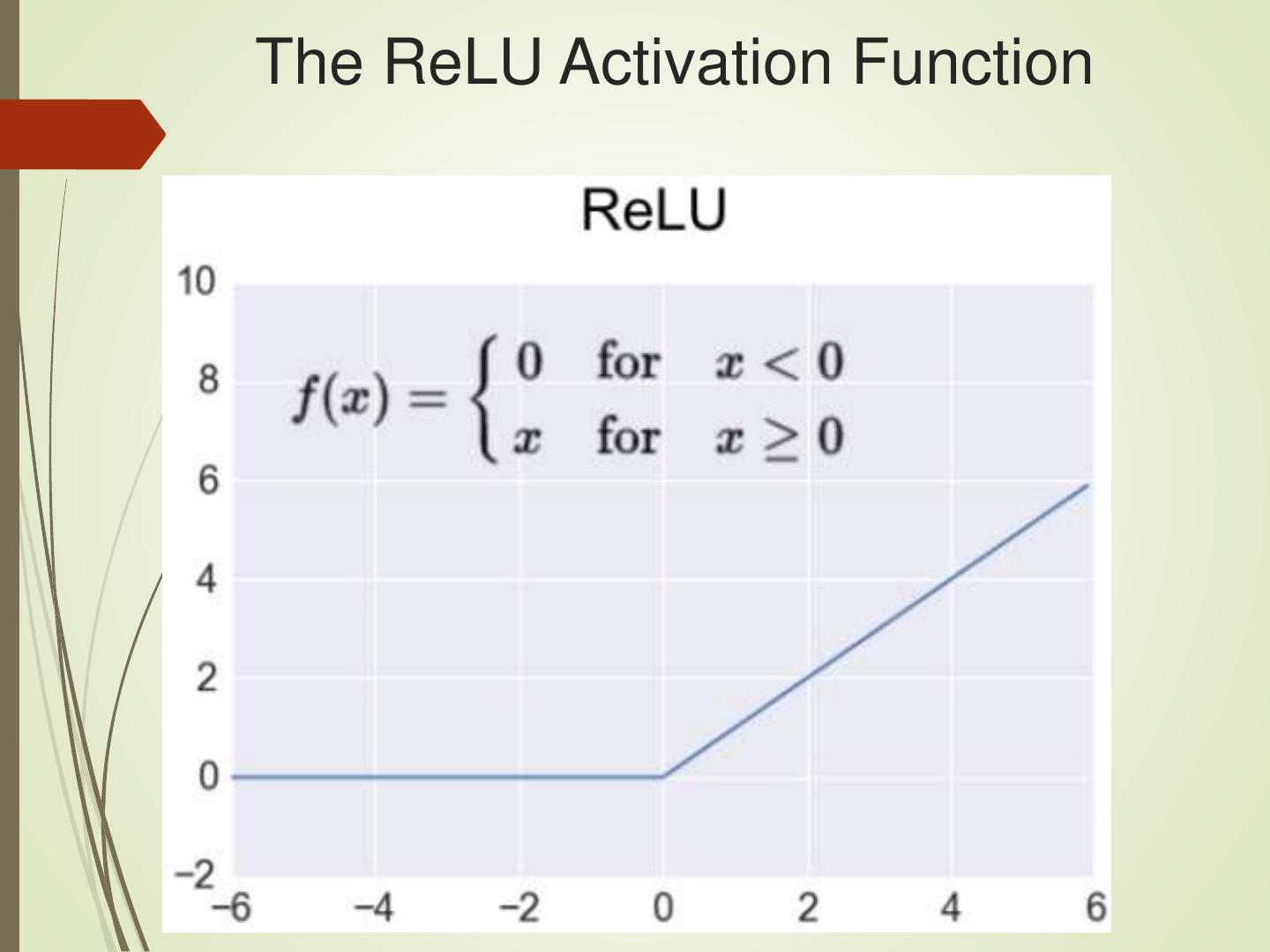
11 .The ReLU Activation Function
12 .The softmax Activation Function
13 . Activation Functions in Python
import numpy as np
...
# Python sigmoid example:
z = 1/(1 + np.exp(-np.dot(W, x)))
...
# Python tanh example:
z = np.tanh(np.dot(W,x));
# Python ReLU example:
z = np.maximum(0, np.dot(W, x))
14 . What’s the “Best” Activation Function?
Initially: sigmoid was popular
Then: tanh became popular
Now: RELU is preferred (better results)
Softmax: for FC (fully connected) layers
NB: sigmoid and tanh are used in LSTMs
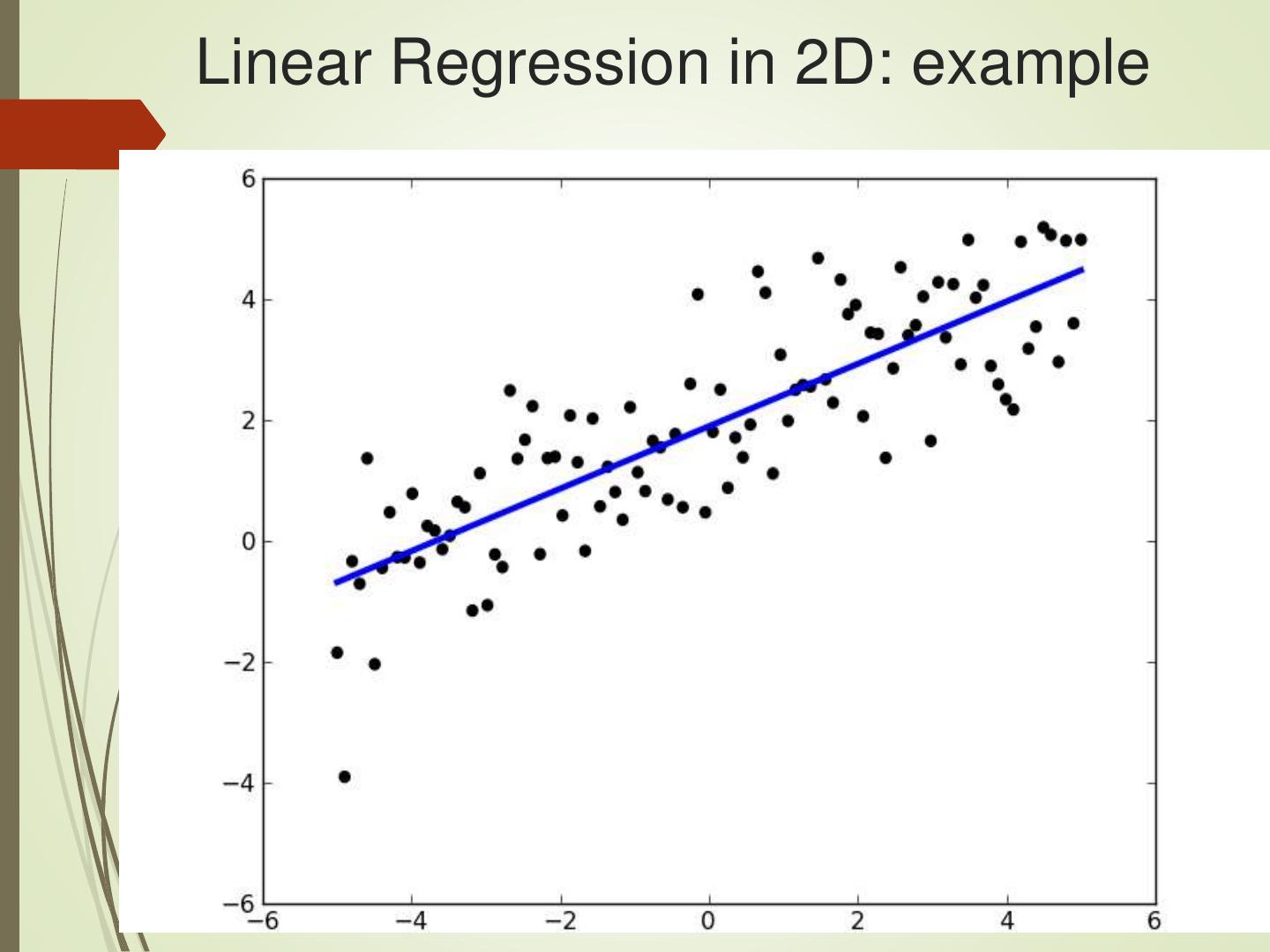
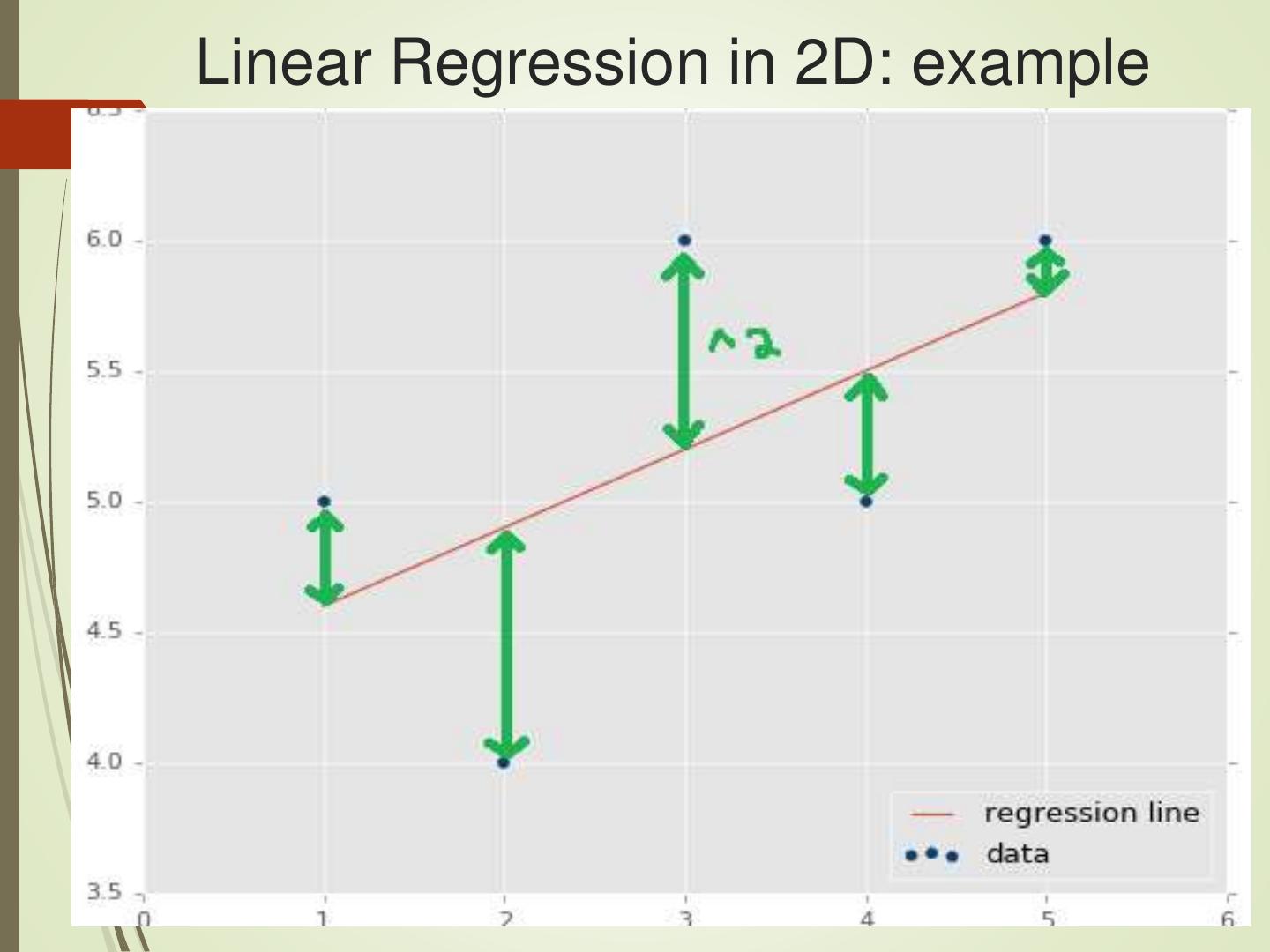
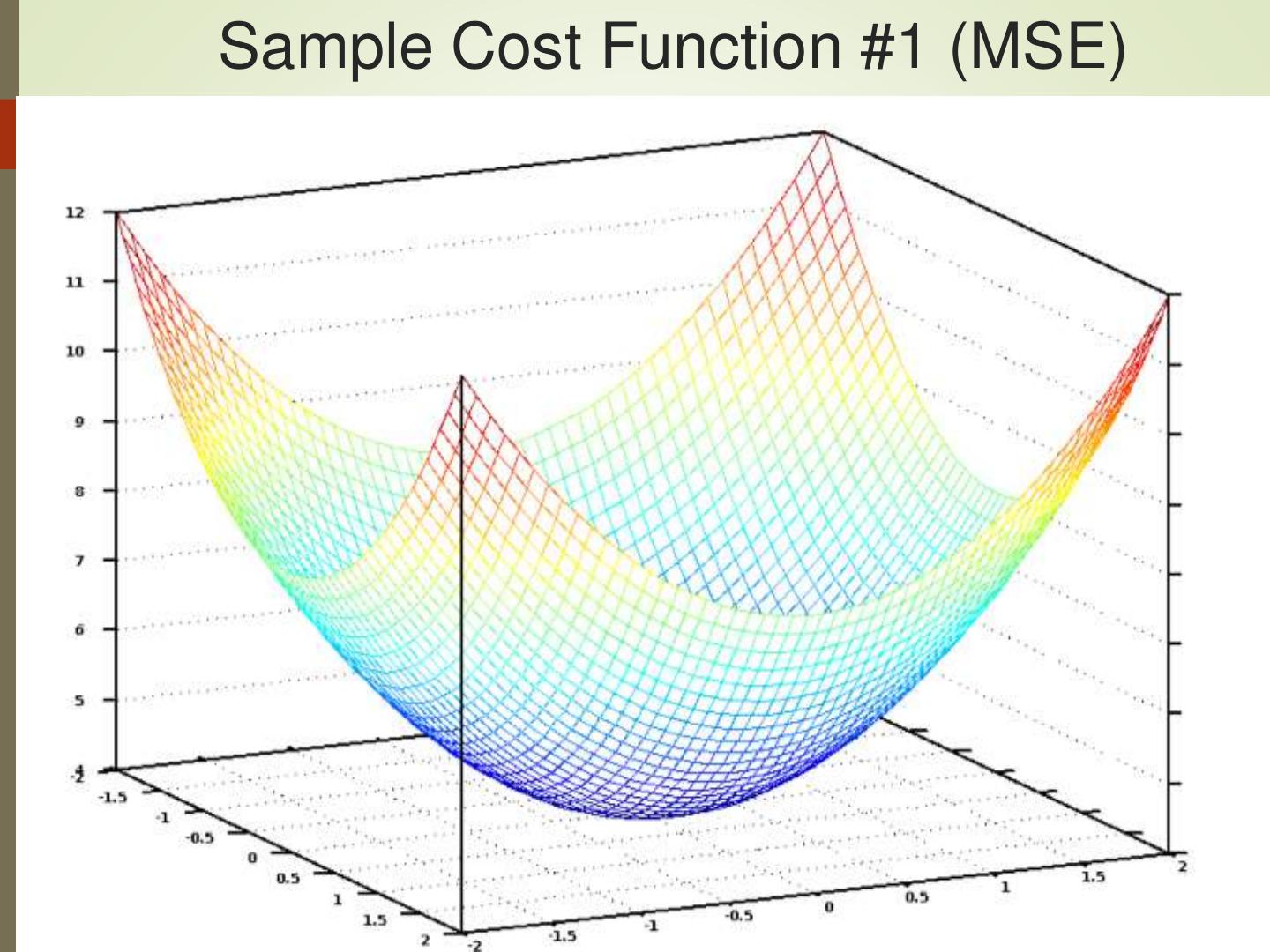
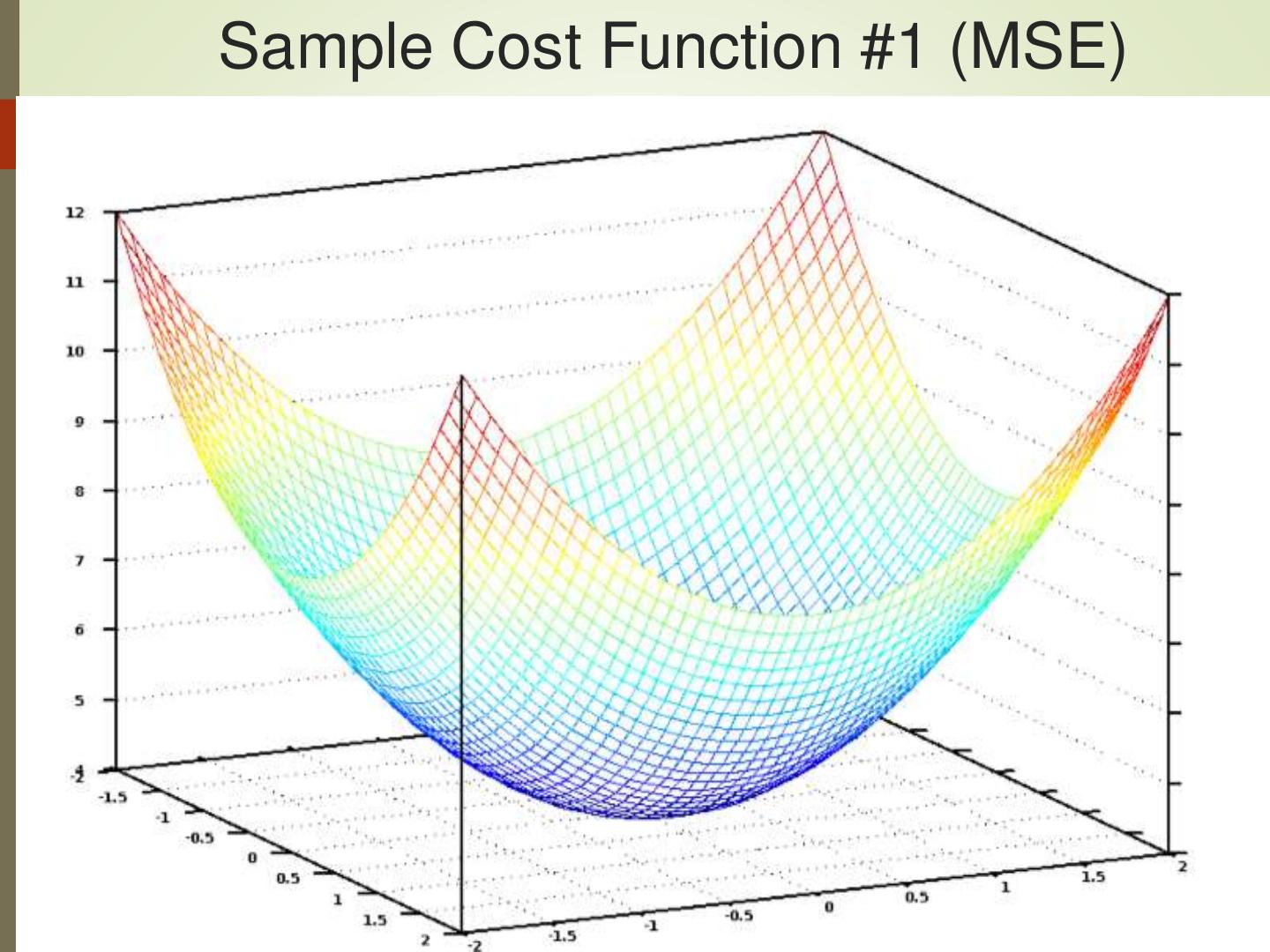
15 . Linear Regression
One of the simplest models in ML
Fits a line (y = m*x + b) to data in 2D
Finds best line by minimizing MSE:
m = slope of the best-fitting line
b = y-intercept of the best-fitting line
16 .Linear Regression in 2D: example
17 .Linear Regression in 2D: example
18 .Sample Cost Function #1 (MSE)
19 . Linear Regression: example #1
One feature (independent variable):
X = number of square feet
Predicted value (dependent variable):
Y = cost of a house
A very “coarse grained” model
We can devise a much better model
20 . Linear Regression: example #2
Multiple features:
X1 = # of square feet
X2 = # of bedrooms
X3 = # of bathrooms (dependency?)
X4 = age of house
X5 = cost of nearby houses
X6 = corner lot (or not): Boolean
a much better model (6 features)
21 . Linear Multivariate Analysis
General form of multivariate equation:
Y = w1*x1 + w2*x2 + . . . + wn*xn + b
w1, w2, . . . , wn are numeric values
x1, x2, . . . , xn are variables (features)
Properties of variables:
Can be independent (Naïve Bayes)
weak/strong dependencies can exist
22 .Sample Cost Function #1 (MSE)
23 .Sample Cost Function #2
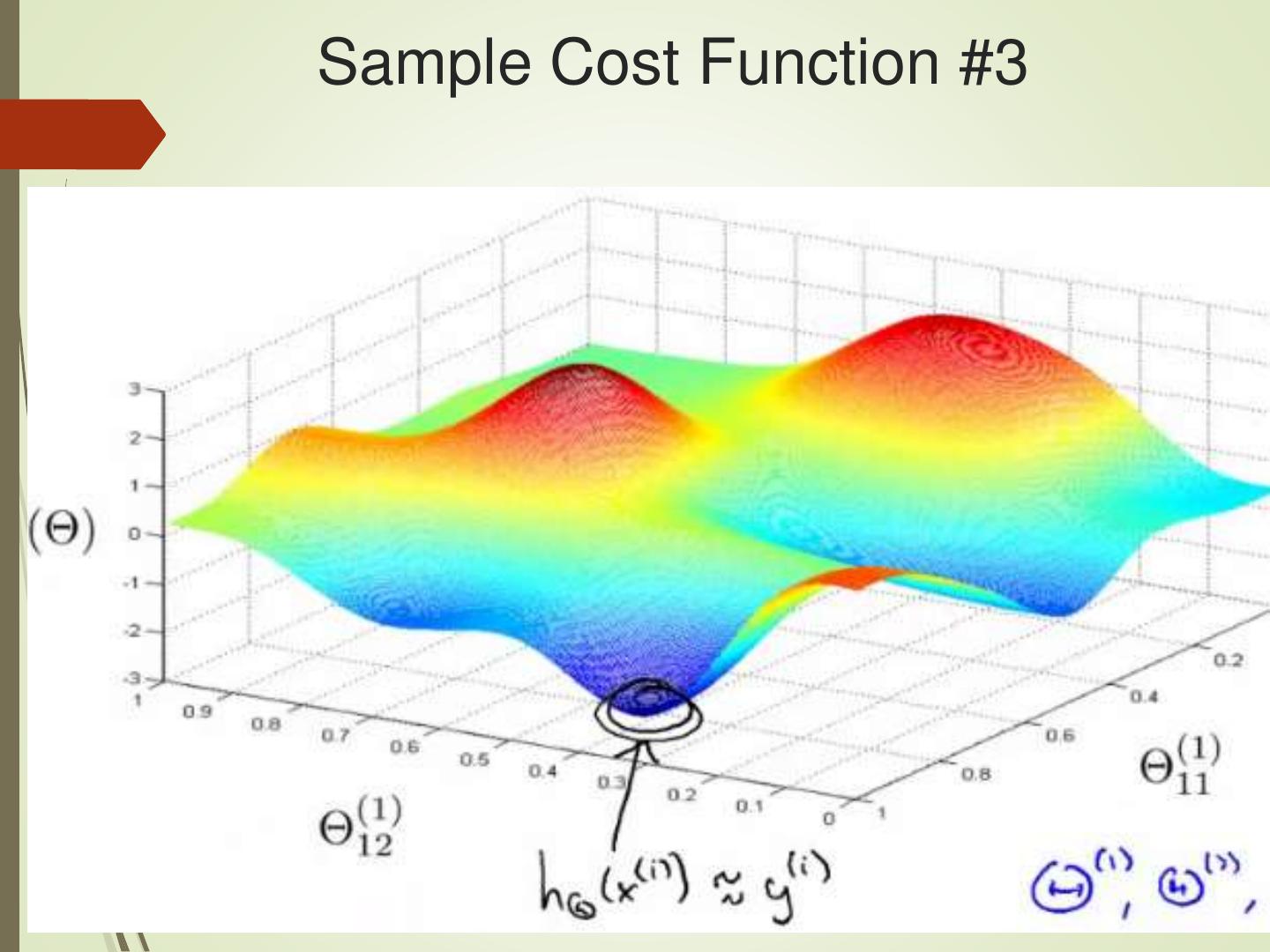
24 .Sample Cost Function #3
25 . Types of Optimizers
SGD
rmsprop
Adagrad
Adam
Others
http://cs229.stanford.edu/notes/cs229-notes1.pdf
26 . Deep Neural Network: summary
input layer, multiple hidden layers, and output layer
nonlinear processing via activation functions
perform transformation and feature extraction
gradient descent algorithm with back propagation
each layer receives the output from previous layer
results are comparable/superior to human experts
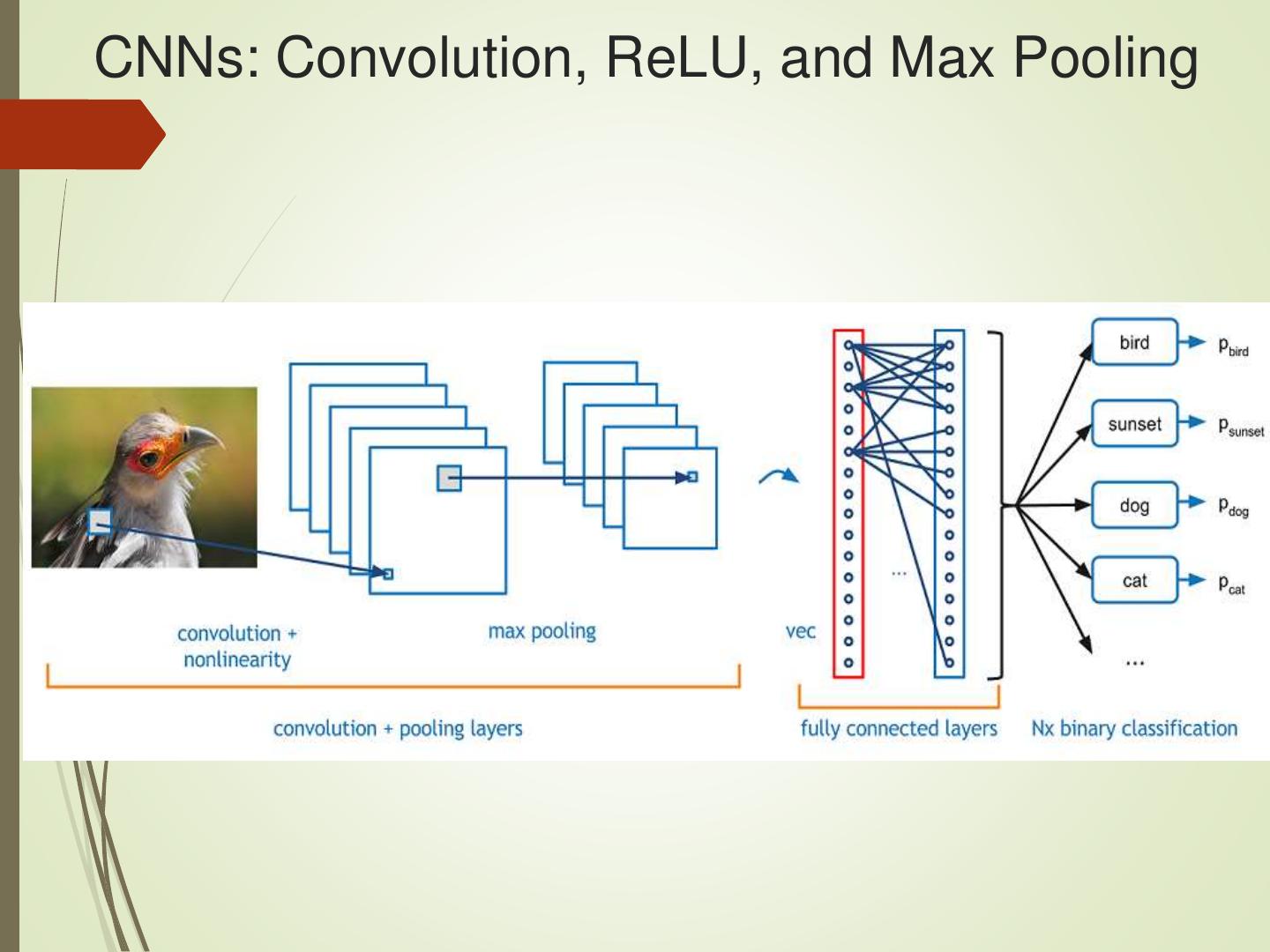
27 . CNNs versus RNNs
CNNs (Convolutional NNs):
Good for image processing
2000: CNNs processed 10-20% of all checks
=> Approximately 60% of all NNs
RNNs (Recurrent NNs):
Good for NLP and audio
Used in hybrid networks
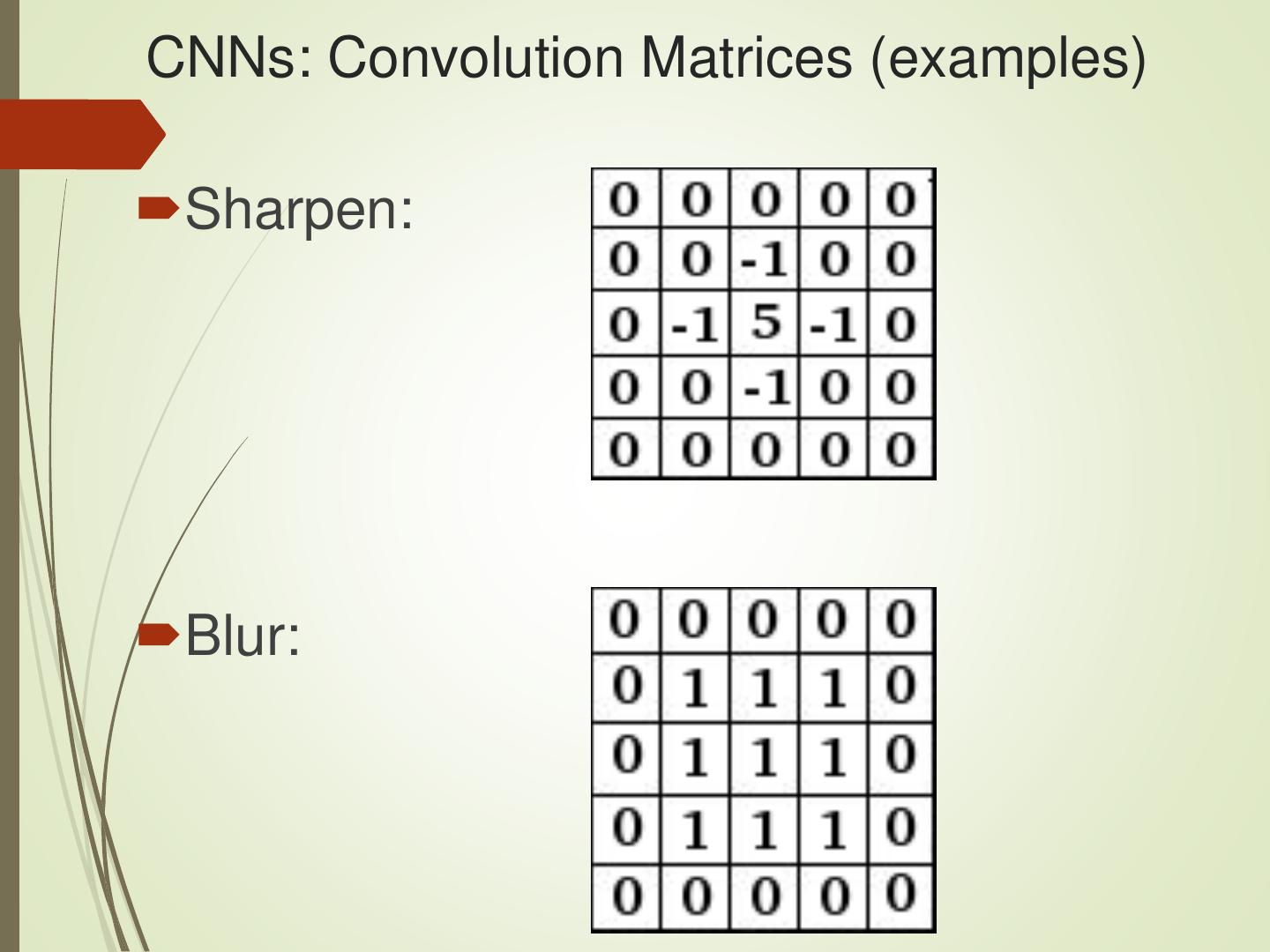
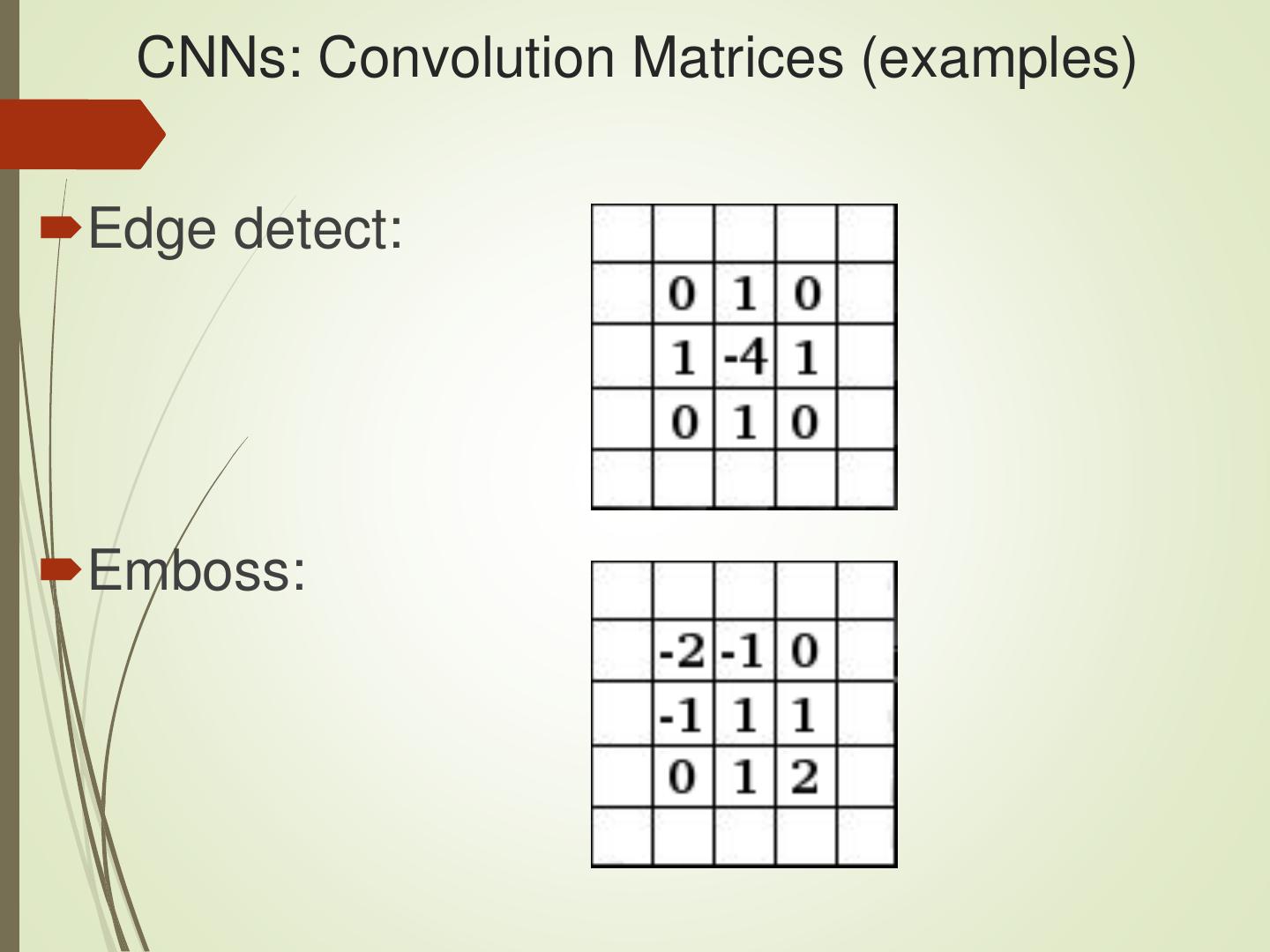
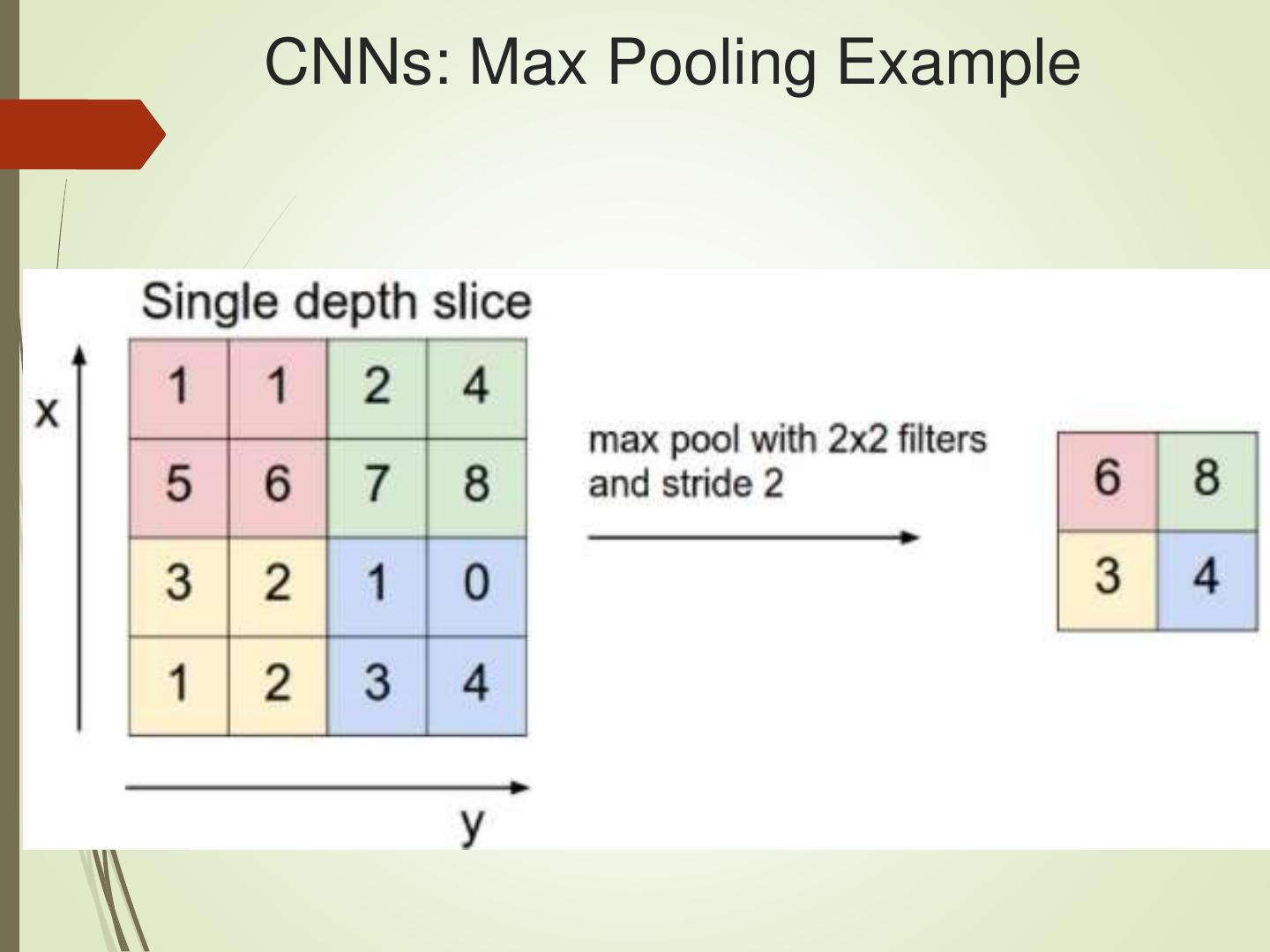
28 .CNNs: Convolution, ReLU, and Max Pooling
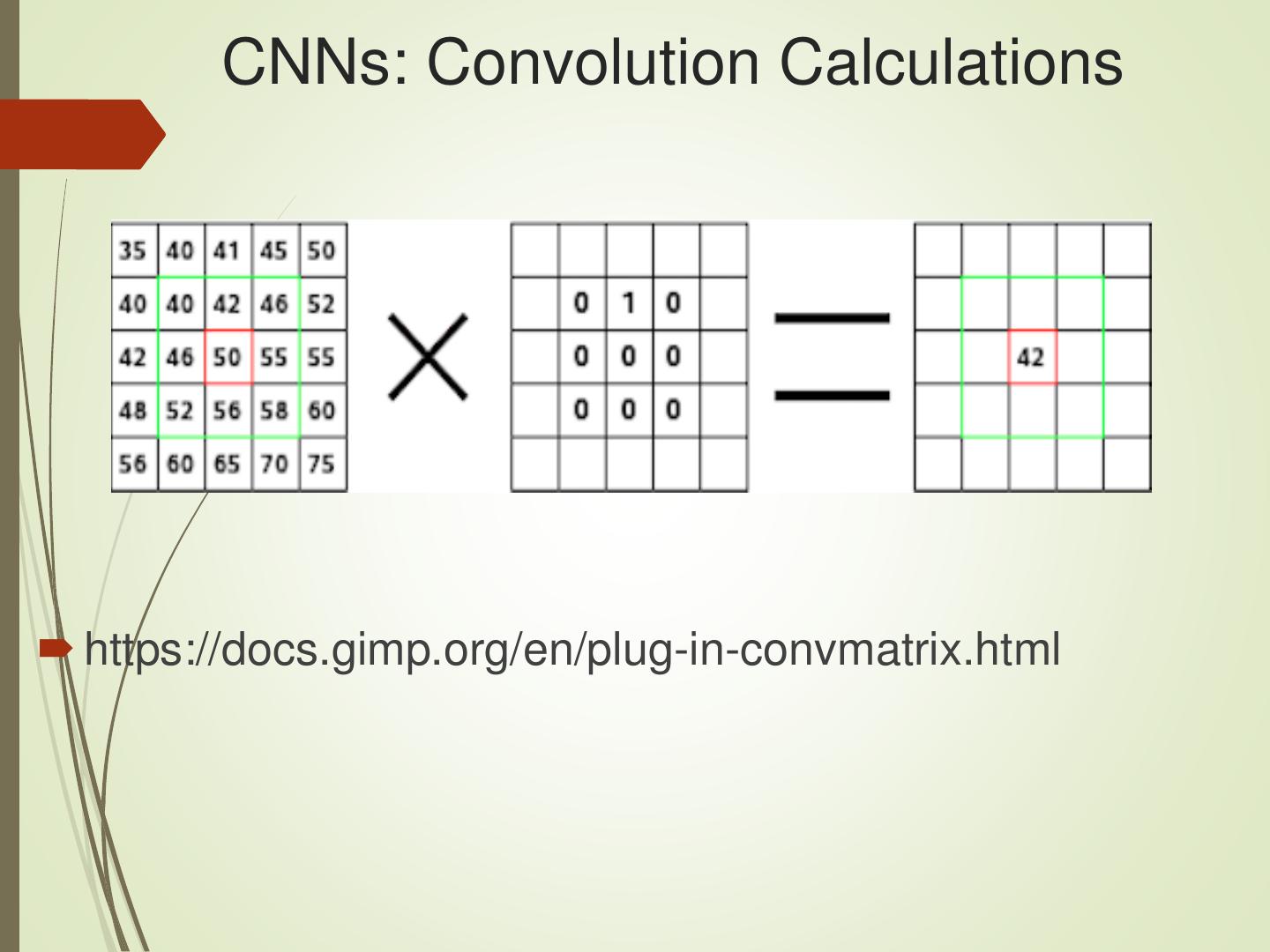
29 . CNNs: Convolution Calculations
https://docs.gimp.org/en/plug-in-convmatrix.html
热门城市
