异构集群上的宏基因组基因聚类优化

1 .异构集群上的宏基因组基因聚类 优化 韦建文 1 , 许志耿 1 , 王丙强 2 , Simon See 1,3 , 林新华 1 1 上海 交通 大学高 性能 计算中心 2 国家超算深圳中心 3 NIVIDIA 2015.11.11 HPC China 2015

2 .提纲 背景介绍 算法描述与性能分析 优化方法 性能分析 结论 2

3 .背景介绍 全基因组将 环境基因 纳入了基因关联分析的范畴，将环境中的基因组按照样本特征进行 聚类 ，进而研究疾病与某些特定基因聚类的 关系 。 特点是样本数量达数千量级，基因数量可达千万量级，涉及大量 浮点迭代运算 。 在单线程处理器上 处理 一千样本和一千万基因大概需要 27 年 。 加速卡技术与异构集群技术日趋完善，尤其是 GPU 提供了大量硬件线程、延迟隐藏技术以及低功耗的单位计算为计算的高度并行化创造了条件。 3

4 .提纲 背景介绍 算法描述与性能分析 优化方法 性能分析 结论 4

5 .算法描述 步骤 1 ： 计算 基因的 检验矩阵 P 步骤 2： 利用 层次聚类 获得初步聚类结果 步骤 3： 使用 高斯混合聚类 获得更加准确、细化的聚类结果 5

6 . 相关性系数 计算 子步骤 1. 对于每个基因 ， 计算基因的检验矩阵 ( O(M 2 N 2 )) 。 6 基因个数 ~5000 样本个数 1267

7 . 相关性系数 计算 7 子步骤 2： 对每个基因， 通过 基因间的检验矩阵 计算 此基因的 特征 值 。 (O(NM 2 ))

8 . 相关性系数 计算 8 子步骤 3： 根据基因的特征 值以及样本间关系， 计算所有 基因 两两之间 的 相关性系数 。 (O(N 2 ))

9 .实验环境： CPU：Intel(R) Xeon(R) E5-2670 @2.60GHz （ 2*8 cores ） Memory：Samsung 8×8GB DDR3 1600MHz Compiler：gcc-4.9.1 OS： Red Hat 6.3 Profiler： Intel Vtune Amplifir XE 2015 相关性计算运行时间分析 9 热点 函数 ： 检验矩阵的 计算 （步骤 1 ） 基因 相关性系数计算（步骤 3 ）

10 .提纲 背景介绍 算法描述与性能分析 优化方法 性能分析 结论 10

11 .优化思路 11

12 .实验环境 12 数据规模 5000 个基因 CPU Intel(R) Xeon(R) E5-2670 @2.60GHz （ 2*8 cores ） GPU Nvidia K20m （ 13 SMs ） 内存 Samsung 8×8GB DDR3 1600MHz 编译器 gcc-4.9.1 & openmpi-1.6.5 & nvcc-5.5 操作系统 Red Hat 6.3 Baseline： 单线程串行程序运行时间

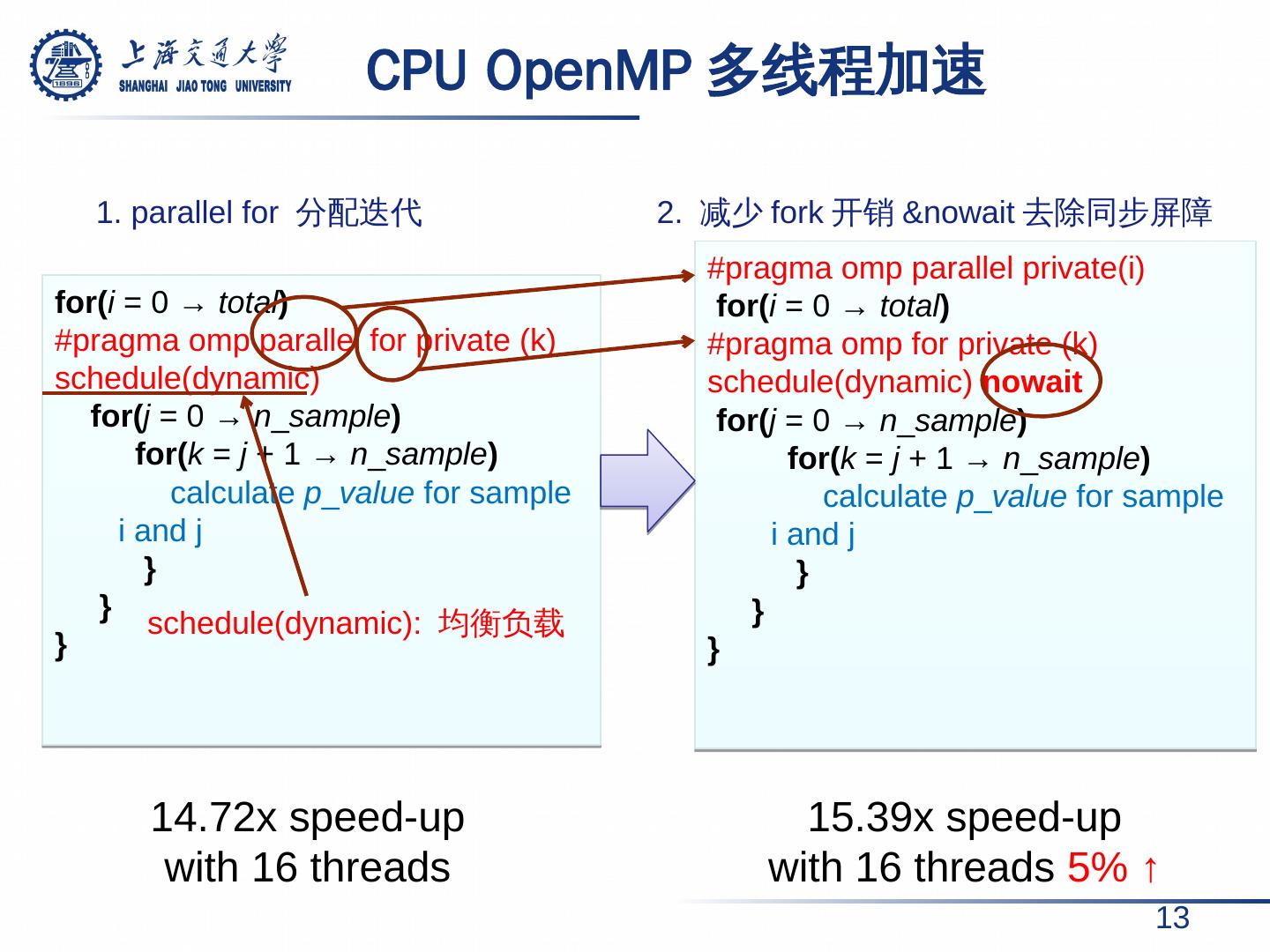
13 . CPU OpenMP 多线程加速 13 for( i = 0 → total ) # pragma omp parallel for private (k) schedule(dynamic) for( j = 0 → n _ sample ) for( k = j + 1 → n _ sample ) calculate p _ value for sample i and j } } } # pragma omp parallel private( i ) for( i = 0 → total ) # pragma omp for private (k) schedule(dynamic) nowait for( j = 0 → n _ sample ) for( k = j + 1 → n _ sample ) calculate p _ value for sample i and j } } } 1. parallel for 分配迭代 2. 减少 fork 开销 &nowait 去除同步屏障 schedule(dynamic): 均衡负载 14.72x speed-up with 16 threads 15.39 x speed-up with 16 threads 5 % ↑

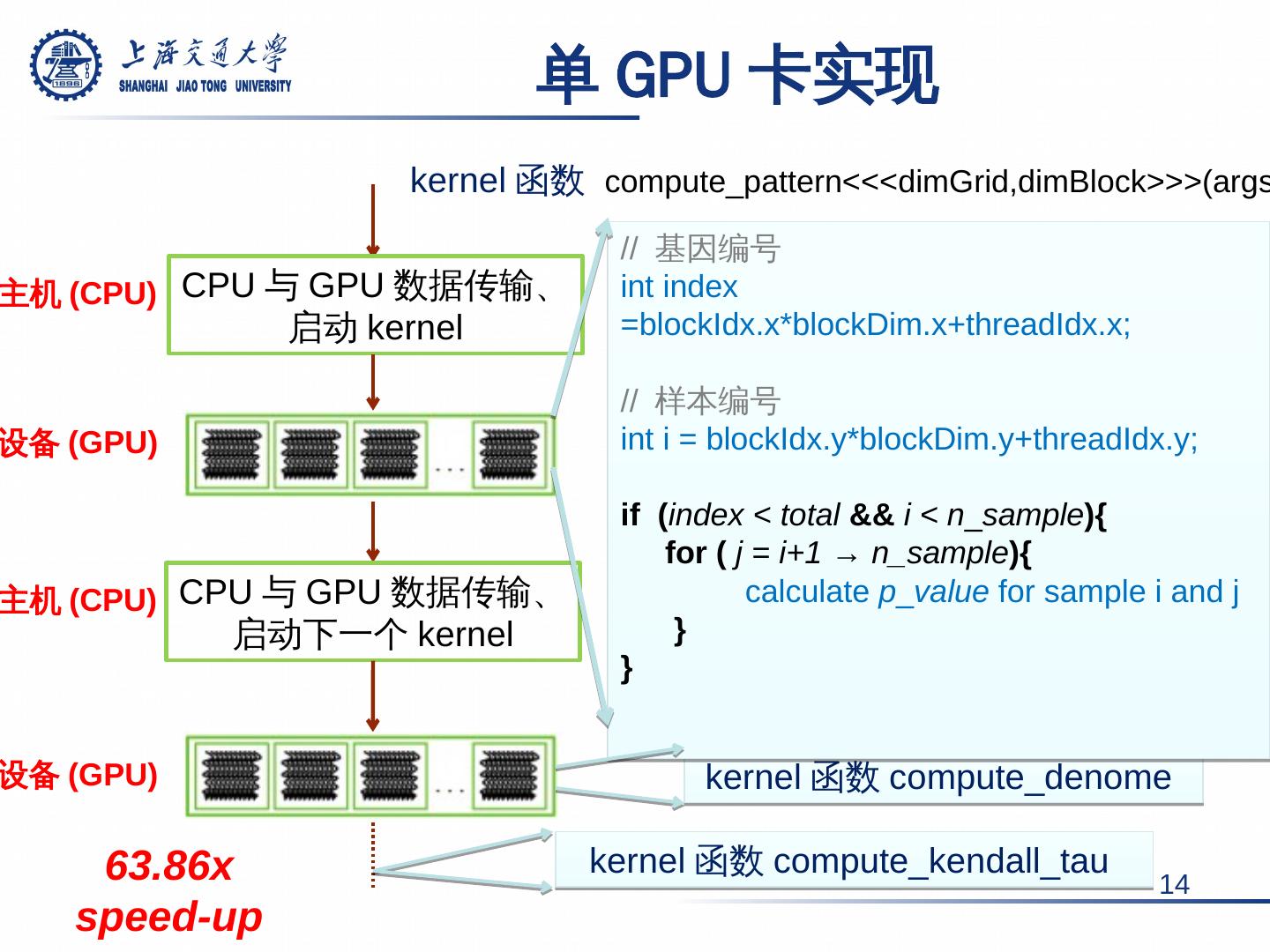
14 .kernel 函数 compute_pattern <<< dimGrid,dimBlock >>>( args ) 单 GPU 卡实现 14 CPU 与 GPU 数据传输、 启动 kernel CPU 与 GPU 数据传输、 启动下一个 kernel 主机 (CPU) 设备 (GPU) 主机 (CPU) kernel 函数 compute_denome kernel 函数 compute_kendall_tau // 基因编号 int index = blockIdx.x * blockDim.x+threadIdx.x ; // 样本编号 int i = blockIdx.y * blockDim.y+threadIdx.y ; if ( index < total && i < n _ sample ){ for ( j = i+1 → n_sample ){ calculate p _ value for sample i and j } } 设备 (GPU) 63.86x speed-up

15 . 单节点上的缓存优化 15 for j in 0, n for ( yb = x; yb < n; yb += BLOCK) # pragma omp for schedule(dynamic) nowait for x in 0, n for y in yb+1, yb+BLOCK p = P_value (w(j, x), w(j, y)) store p to p(j, x, y) end for end for end for end for i = blockIdx.x * blockDim.x+threadIdx.x x = blockIdx.y * blockDim.x + threadIdx.x if i <= m && x <= n for k in x/BLOCK, m/BLOCK LOAD to shared for y in k*BLOCK, (k+1)*BLOCK p = P_value (w(x, j), w(y, j)) store p to p(j, x, y) end for WRITE p(j, x, y) TO global end for end if CPU 上的 Cache Blocking GPU 上利用 shared memory 做 Cache Blocking (Tiling) 优化后 CPU 版获得 1.6x 加速 优化后 GPU 版获得 1.8x 加速

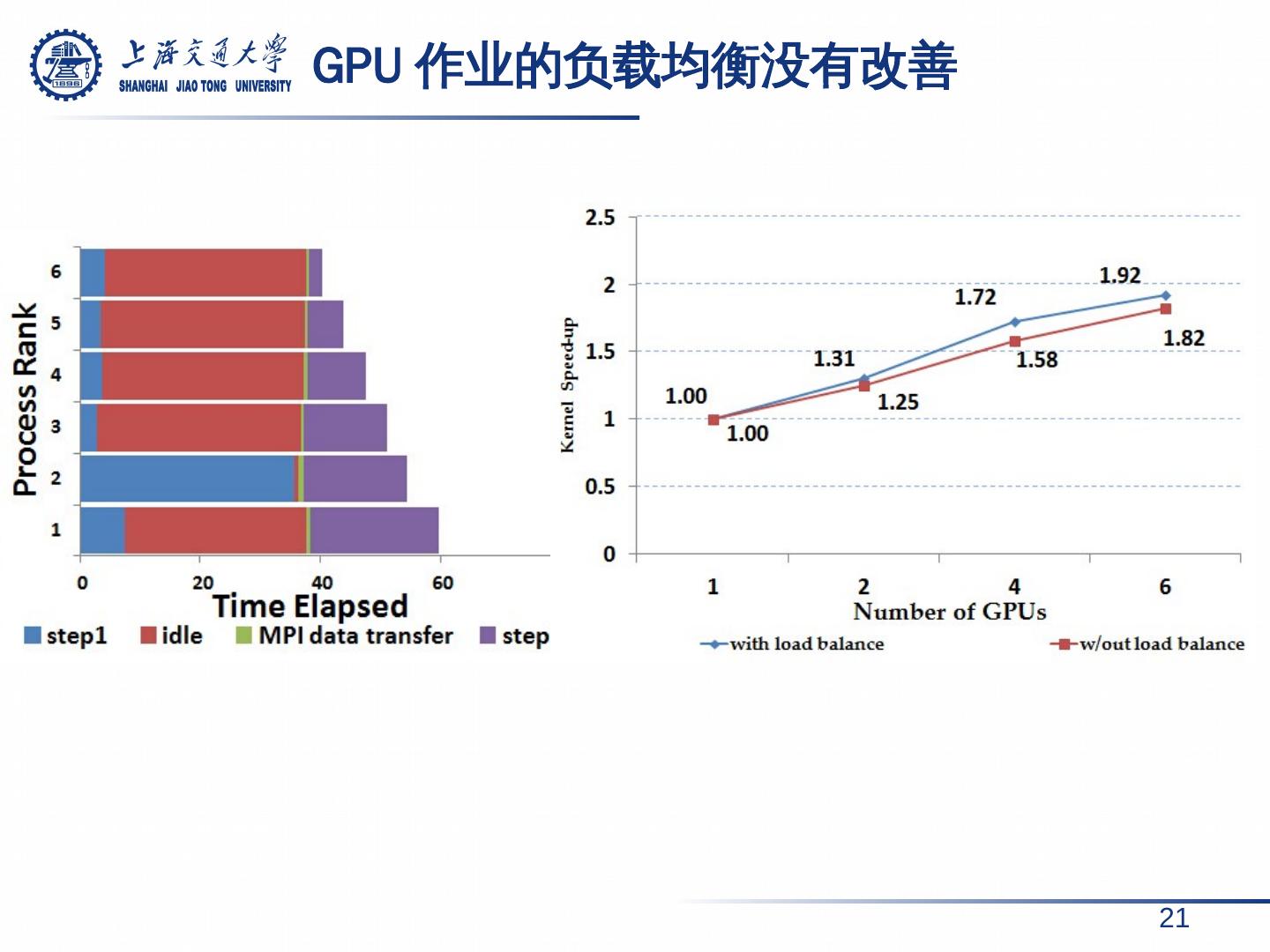
16 . MPI 的多节点扩展 16 问题分解与数据通信 多节点工作模式 问题分解 内部并行 同 步、 数据汇集 相比于单节点 ， 16 节点获得了 6.42 x 加速。 相比于单卡， 6GPU 卡仅获得了 1.8x 加速。

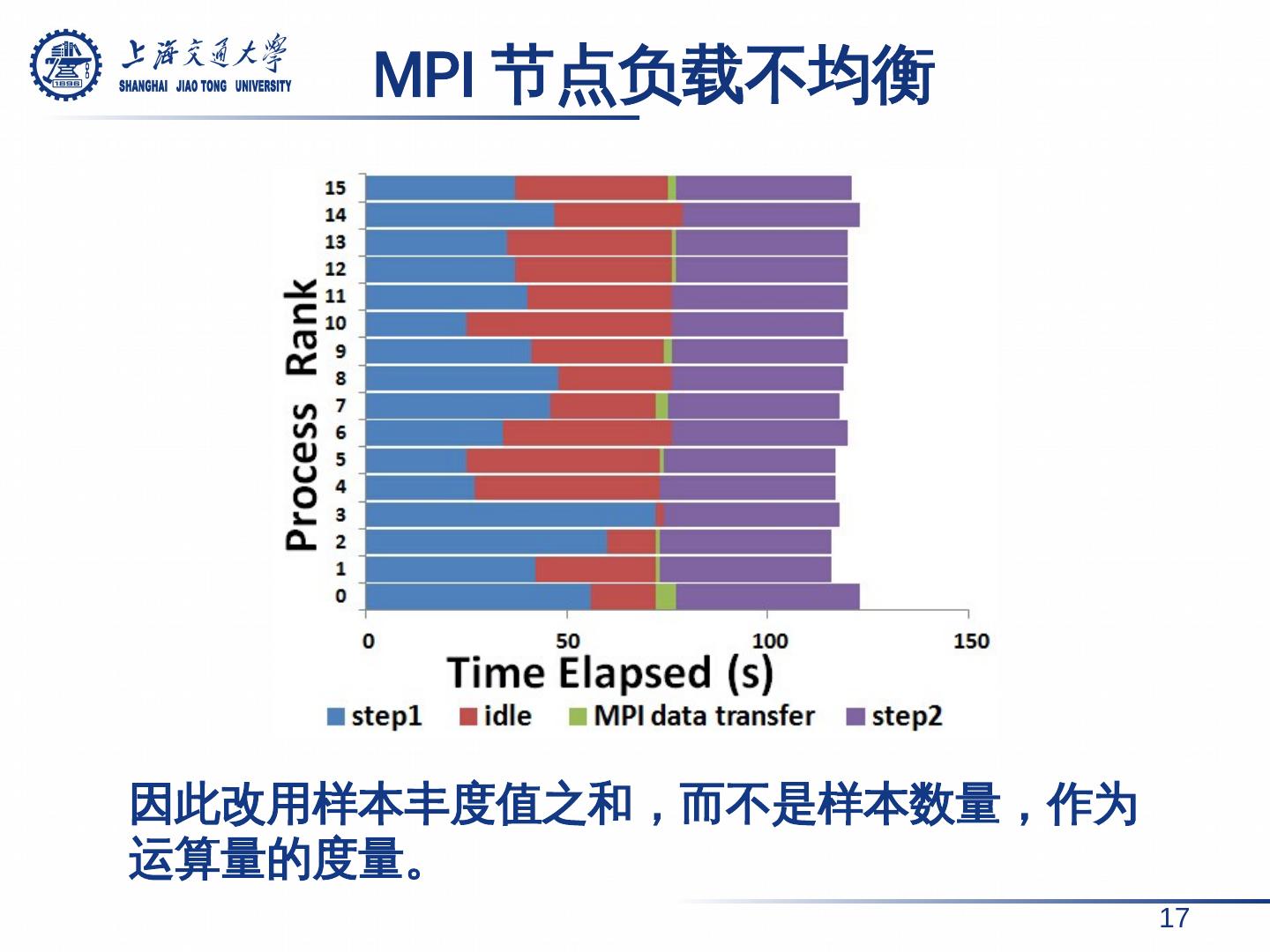
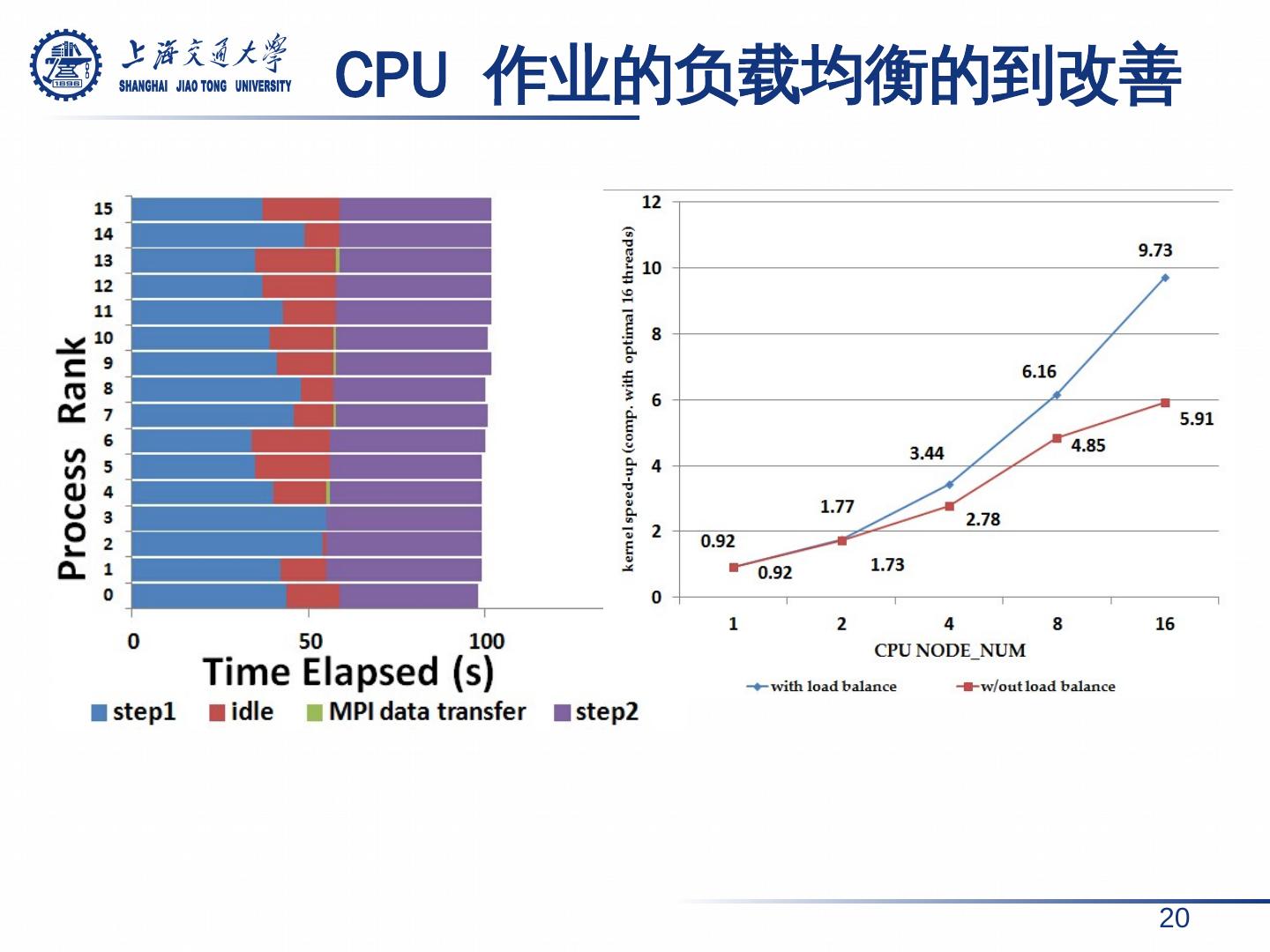
17 .因此改用样本丰度值之和 ，而不是样本数量，作为运算量的度量。 MPI 节点负载不均衡 17

18 .提纲 背景介绍 算法描述与性能分析 优化方法 性能分析 结论 18

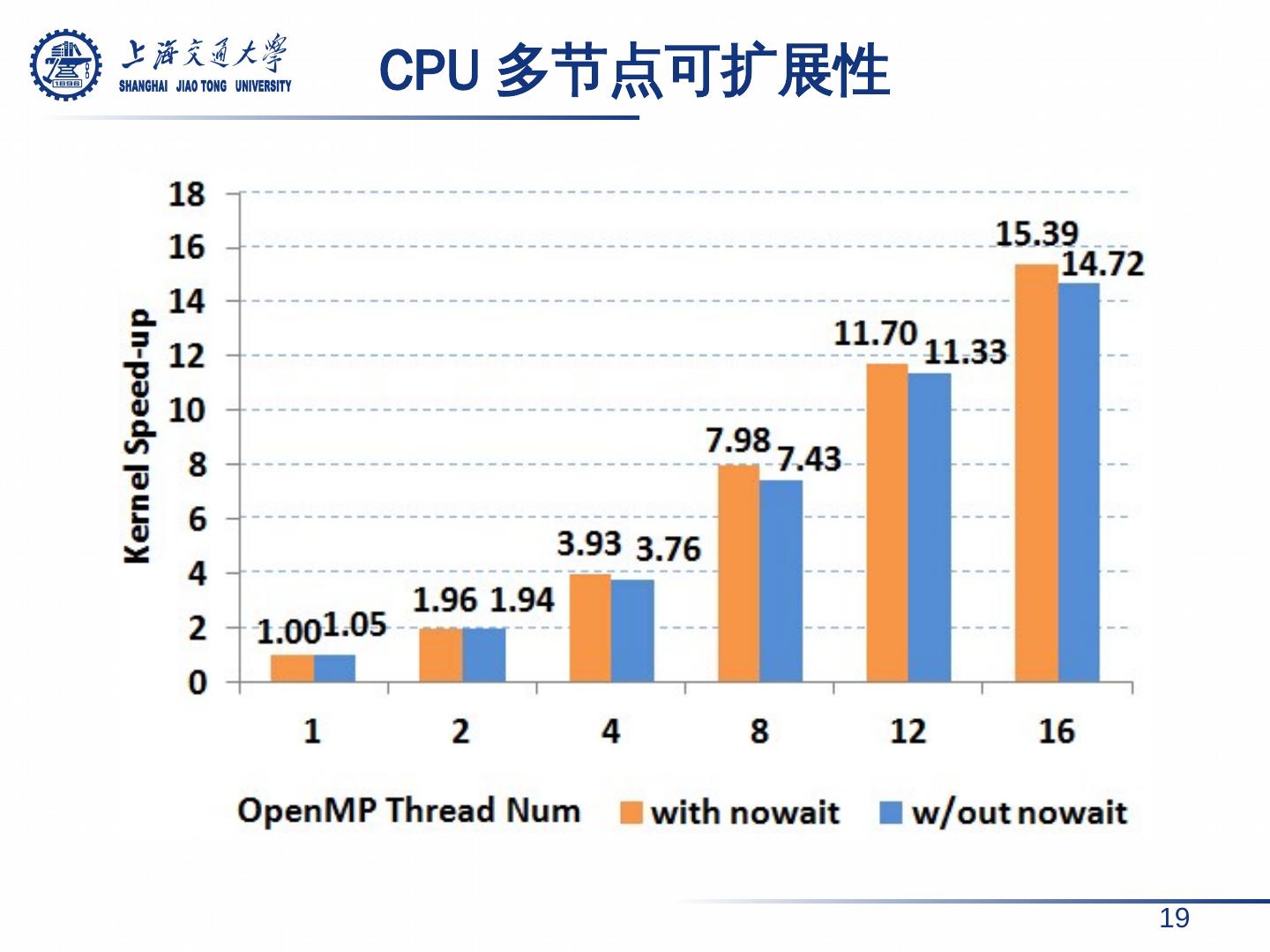
19 .CPU 多节点可扩展性 19

20 . CPU 作业的负载均衡的到改善 20

21 .GPU 作业的负载均衡没有改善 21

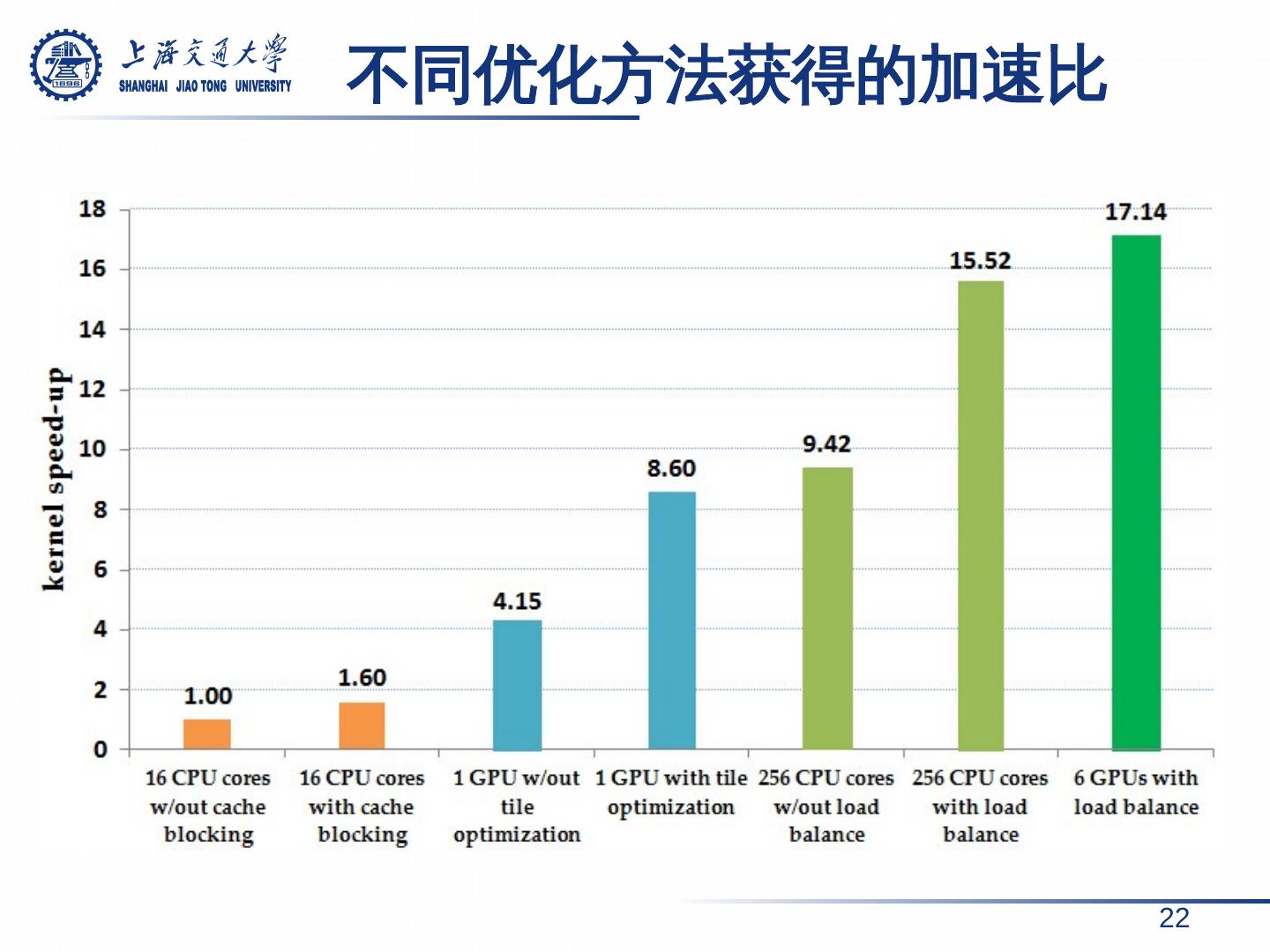
22 . 不同优化方法获得的加速比 22

23 .提纲 背景介绍 算法描述与性能分析 优化方法 性能分析 结论 23

24 .结论 相 关性系数计算是 基于距离 的聚类算法共有的特性，因此对相关性系数计算进行并行化对优化聚类算法具有借鉴意义。 经 过一系列优化 ， 以单节点 16 线程版本为性能基准， 我们 在 16 个 CPU 节点 上获得 了 15.52 倍 的性能提升， 在 6 个 GPU 节点 上获得 了 17.14 倍 的性能提升。 在 未来的工作中，我们会 改进 负 载分配 算法 ，减少 通信开销 （减少冗余数据传输、增大网络带宽等）， 并且尝试更多的加速方法以进一步提高多节点上的 程序 性能。 24

25 .谢谢！

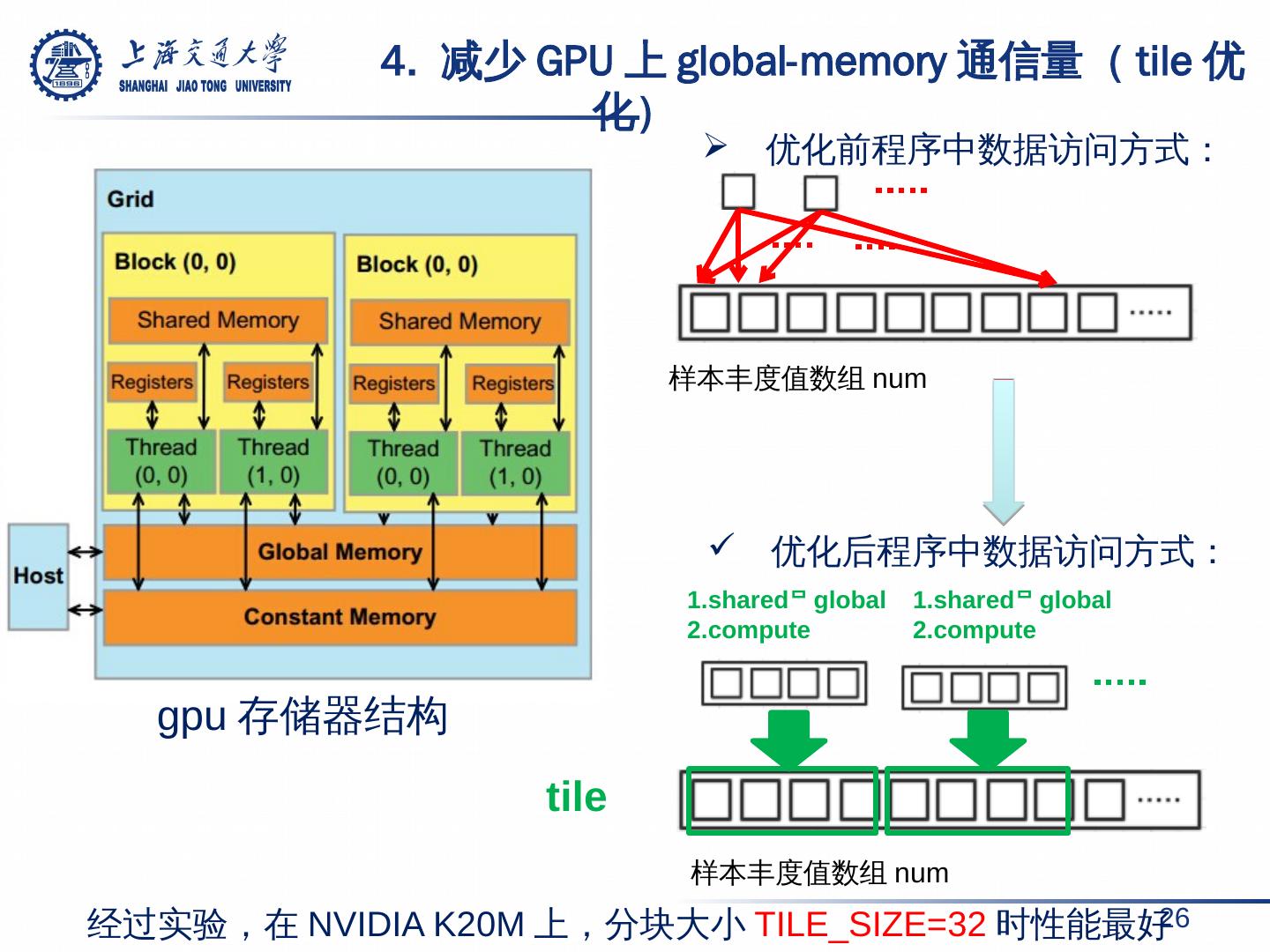
26 . 4. 减少 GPU 上 global-memory 通信量（ tile 优化） 26 gpu 存储器结构 样本丰度值数组 num 样本丰度值数组 num 1.shared global2. compute 1.shared global 2. compute 优化前程序中数据访问方式： 优化后程序中数据访问方式： 经过实验，在 NVIDIA K20M 上，分块大小 TILE_SIZE=32 时性能最好 tile

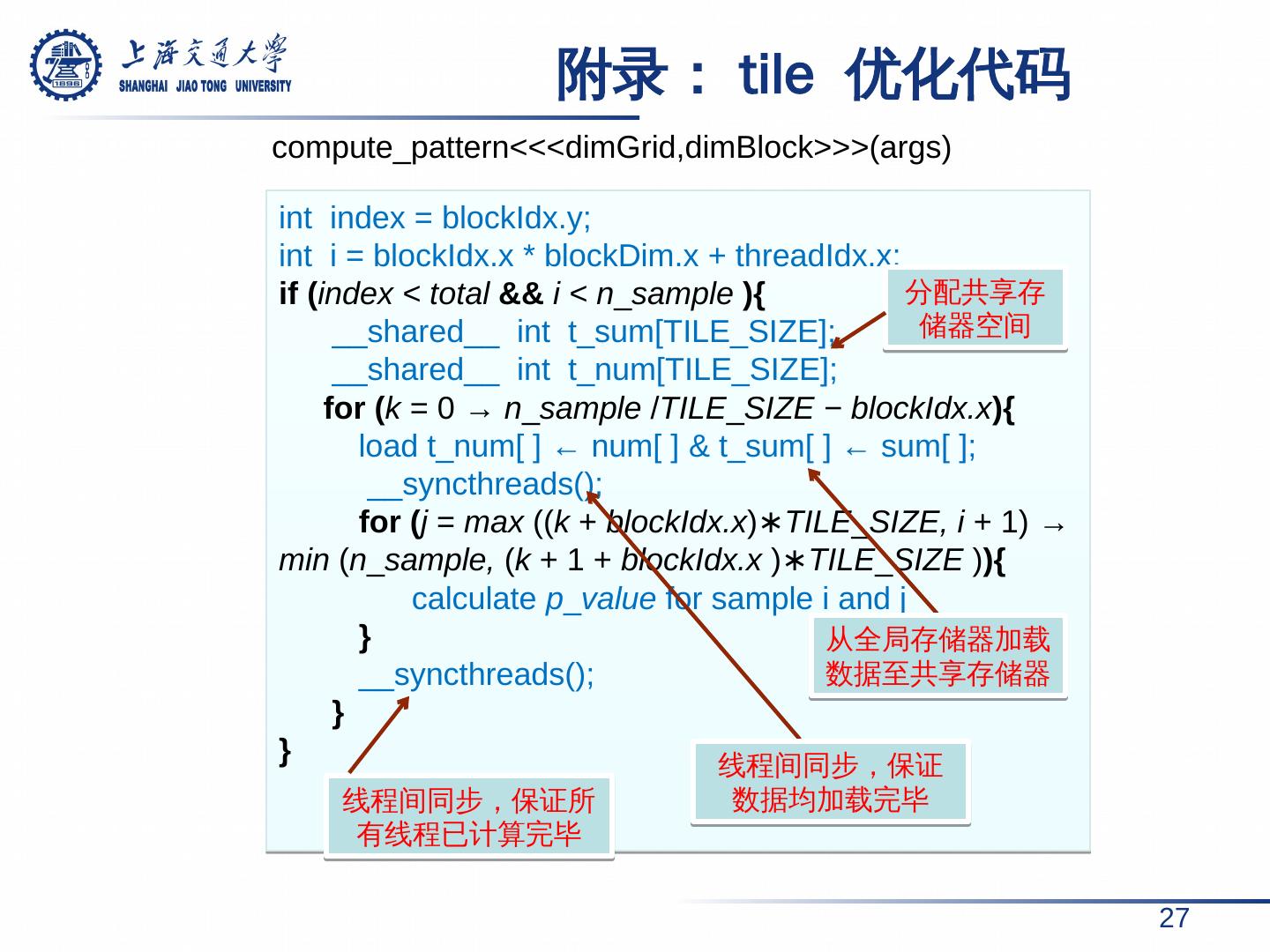
27 . 附录： tile 优化代码 27 int index = blockIdx.y ; int i = blockIdx.x * blockDim.x + threadIdx.x ; if ( index < total && i < n _ sample ){ __shared__ int t_sum [TILE_SIZE]; __shared__ int t_num [TILE_SIZE]; for ( k = 0 → n _ sample / TILE _ SIZE − blockIdx.x ){ load t_num [ ] ← num[ ] & t_sum [ ] ← sum[ ]; __ syncthreads (); for ( j = max (( k + blockIdx.x ) ∗TILE _ SIZE, i + 1) → min ( n _ sample , ( k + 1 + blockIdx.x ) ∗TILE _ SIZE ) ){ calculate p _ value for sample i and j } __ syncthreads (); } } 分配共享存储器空间 线程间同步，保证所有线程已计算完毕 compute_pattern <<< dimGrid,dimBlock >>>( args ) 从全局存储器加载数据至共享存储器 线程间同步，保证数据均加载完毕

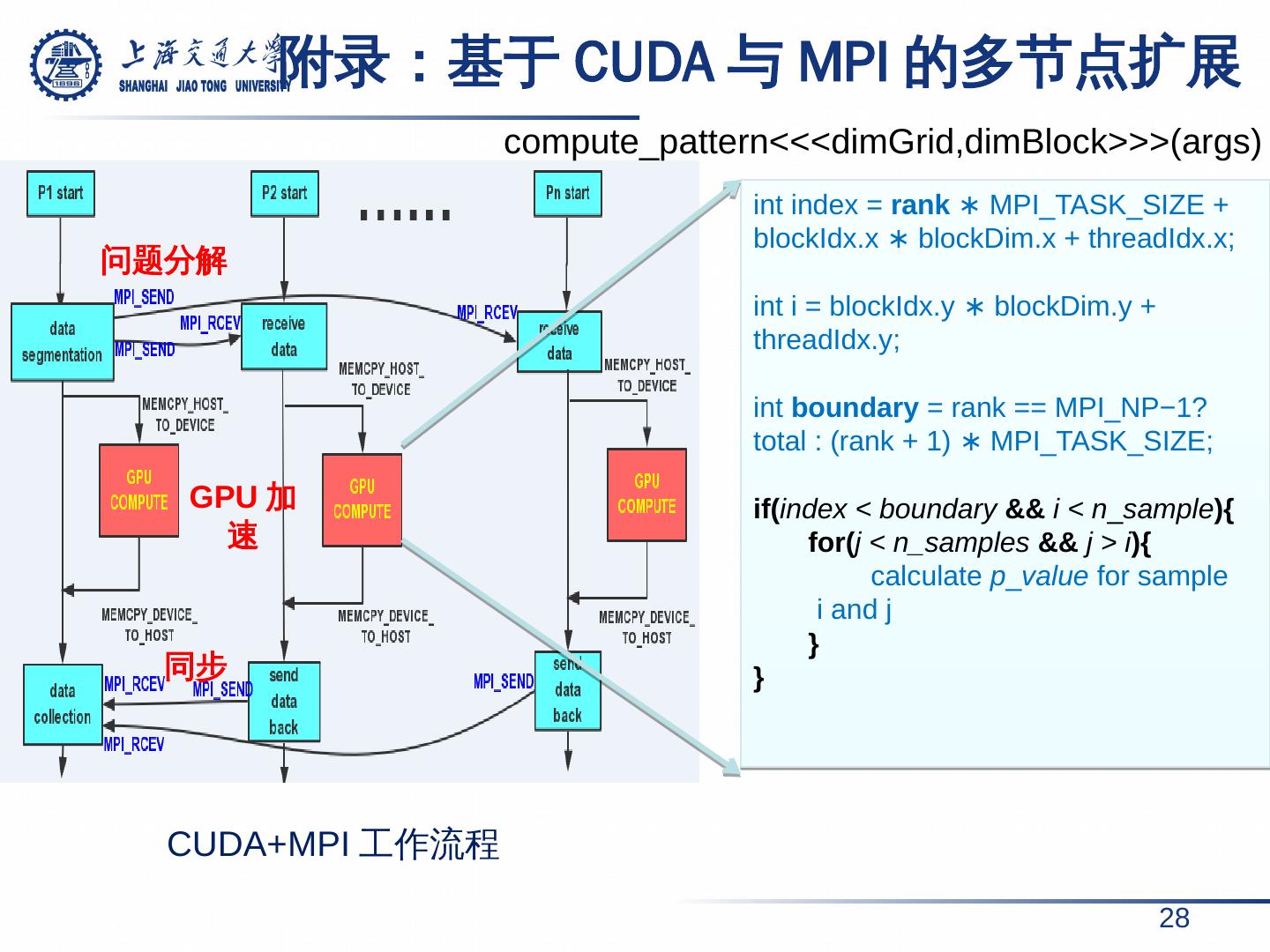
28 . 附录： 基于 CUDA 与 MPI 的多节点扩展 28 CUDA+MPI 工作流程 int index = rank ∗ MPI_TASK_SIZE + blockIdx.x ∗ blockDim.x + threadIdx.x ; int i = blockIdx.y ∗ blockDim.y + threadIdx.y ; int boundary = rank == MPI_NP−1? total : (rank + 1) ∗ MPI_TASK_SIZE; if( index < boundary && i < n _ sample ){ for( j < n_samples && j > i ){ calculate p _ value for sample i and j } } compute_pattern<<<dimGrid,dimBlock>>>(args) 问题分解 GPU 加速 同步

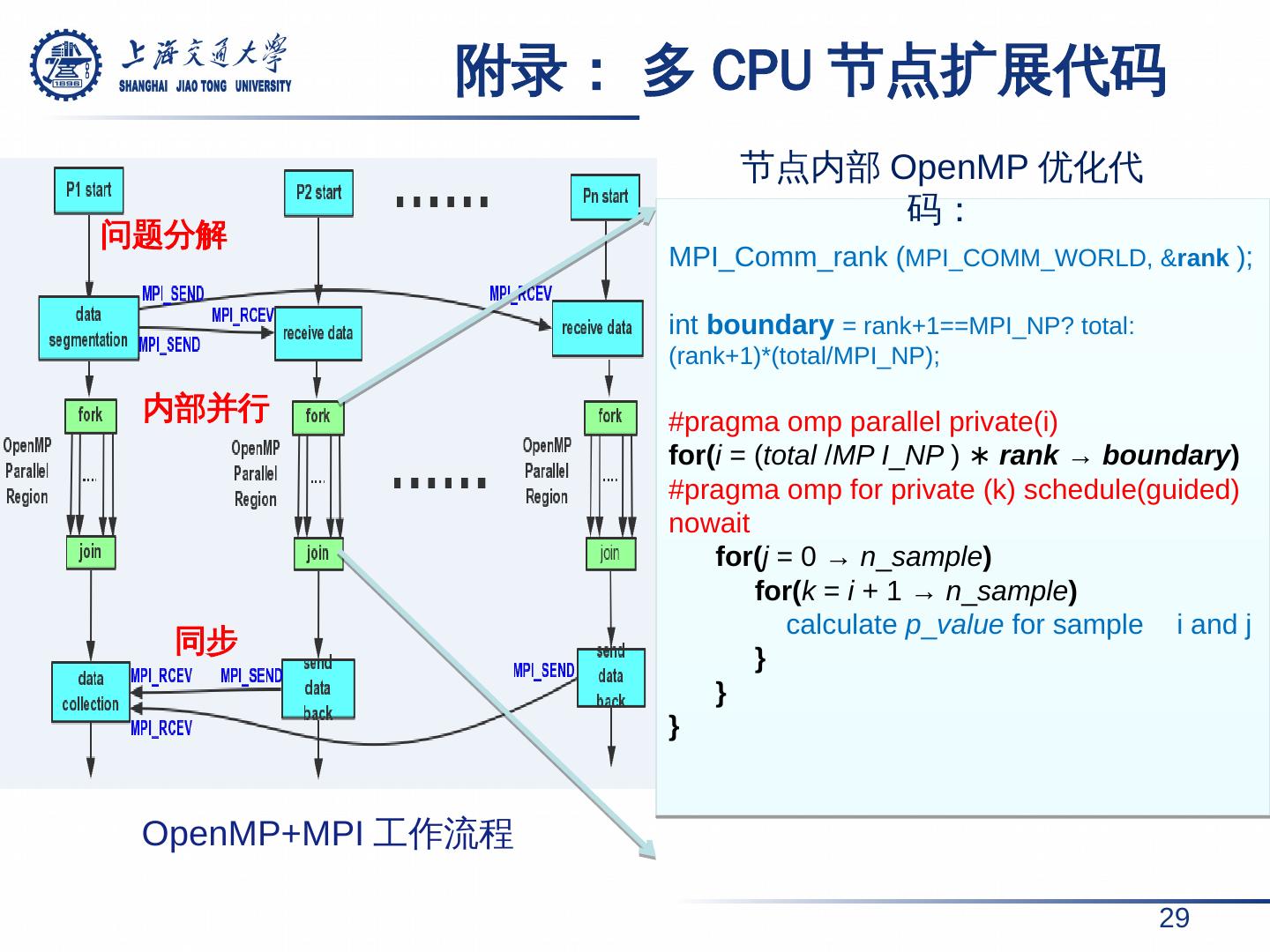
29 . 附录： 多 CPU 节点扩展代码 29 OpenMP+MPI 工作流程 MPI_Comm_rank ( MPI_COMM_WORLD, & rank ); int boundary = rank+1==MPI_NP? total:(rank+1)*(total/MPI_NP); # pragma omp parallel private( i ) for( i = ( total / MP I _ NP ) ∗ rank → boundary ) # pragma omp for private (k) schedule(guided) nowait for( j = 0 → n _ sample ) for( k = i + 1 → n _ sample ) calculate p _ value for sample i and j } } } 节点内部 OpenMP 优化代码： 问题分解 内部并行 同步