Massively Parallel Sort-Merge Joins in Main Memory Multi-Core DB

1 .Massively Parallel Sort-Merge Joins (MPSM) in Main Memory Multi-Core Database Systems Martina Albutiu, Alfons Kemper, and Thomas Neumann Technische Universität München

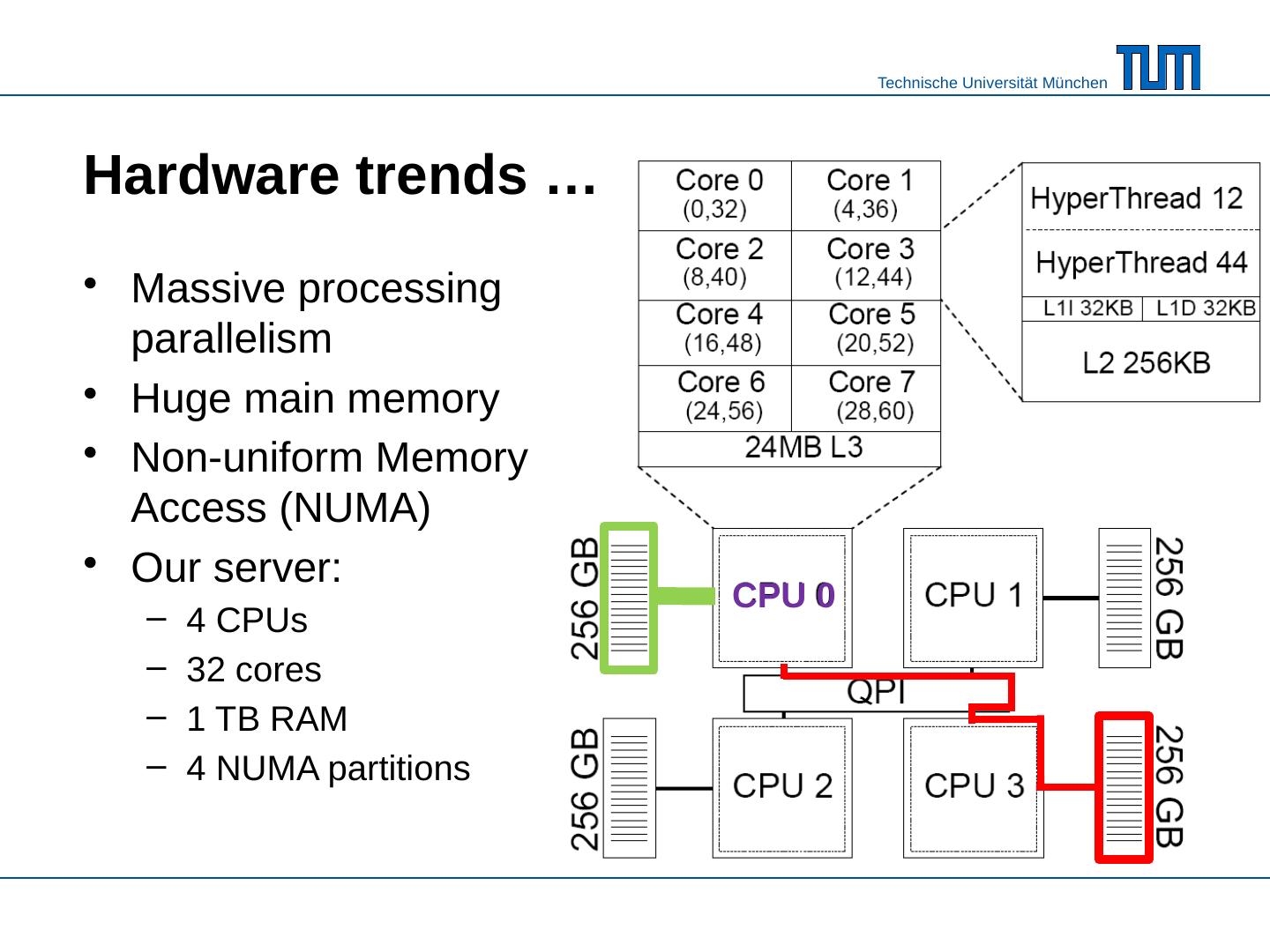
2 .Hardware trends … Massive processing parallelism Huge main memory Non-uniform Memory Access (NUMA) Our server : 4 CPUs 32 cores 1 TB RAM 4 NUMA partitions CPU 0

3 .Main memory database systems VoltDB , SAP HANA, MonetDB HyPer *: real-time business intelligence queries on transactional data * http://www-db.in.tum.de/HyPer/ ICDE 2011 A. Kemper, T. Neumann MPSM for efficient OLAP query processing

4 .How to exploit these hardware trends ? Parallelize algorithms Exploit fast main memory access  Kim, Sedlar , Chhugani : Sort vs. Hash Revisited : Fast Join Implementation on Modern Multi-Core CPUs . VLDB‘09  Blanas , Li, Patel: Design and Evaluation of Main Memory Hash Join Algorithms for Multi- core CPUs . SIGMOD‘11 AND be aware of fast local vs. slow remote NUMA access

5 .How much difference does NUMA make ? 100% scaled execution time sort partitioning merge join ( sequential read ) 22756 ms 417344 ms 1000 ms 7440 ms 837 ms 12946 ms remote local synchronized sequential remote local 22756 ms 7440 ms 417344 ms

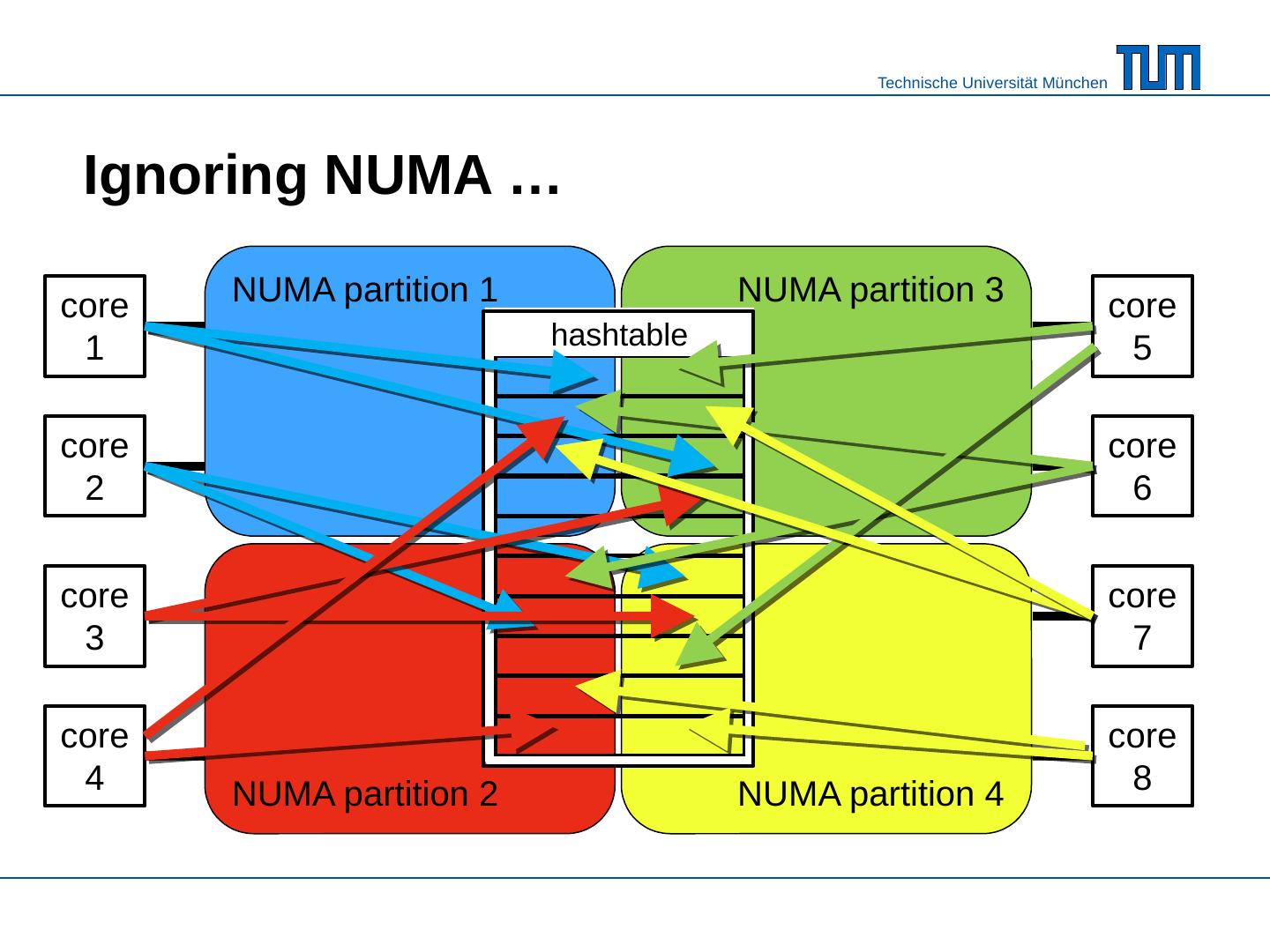
6 .NUMA partition 1 NUMA partition 3 NUMA partition 2 NUMA partition 4 hashtable Ignoring NUMA … core 1 core 2 core 3 core 4 core 5 core 6 core 7 core 8

7 .The three NUMA commandments C1 Thou shalt not write thy neighbor‘s memory randomly -- chunk the data , redistribute , and then sort / work on your data locally . C2 Thou shalt read thy neighbor‘s memory only sequentially -- let the prefetcher hide the remote access latency . C3 Thou shalt not wait for thy neighbors -- don‘t use fine-grained latching or locking and avoid synchronization points of parallel threads .

8 .Basic idea of MPSM private R public S chunk private R chunk public S R chunks S chunks

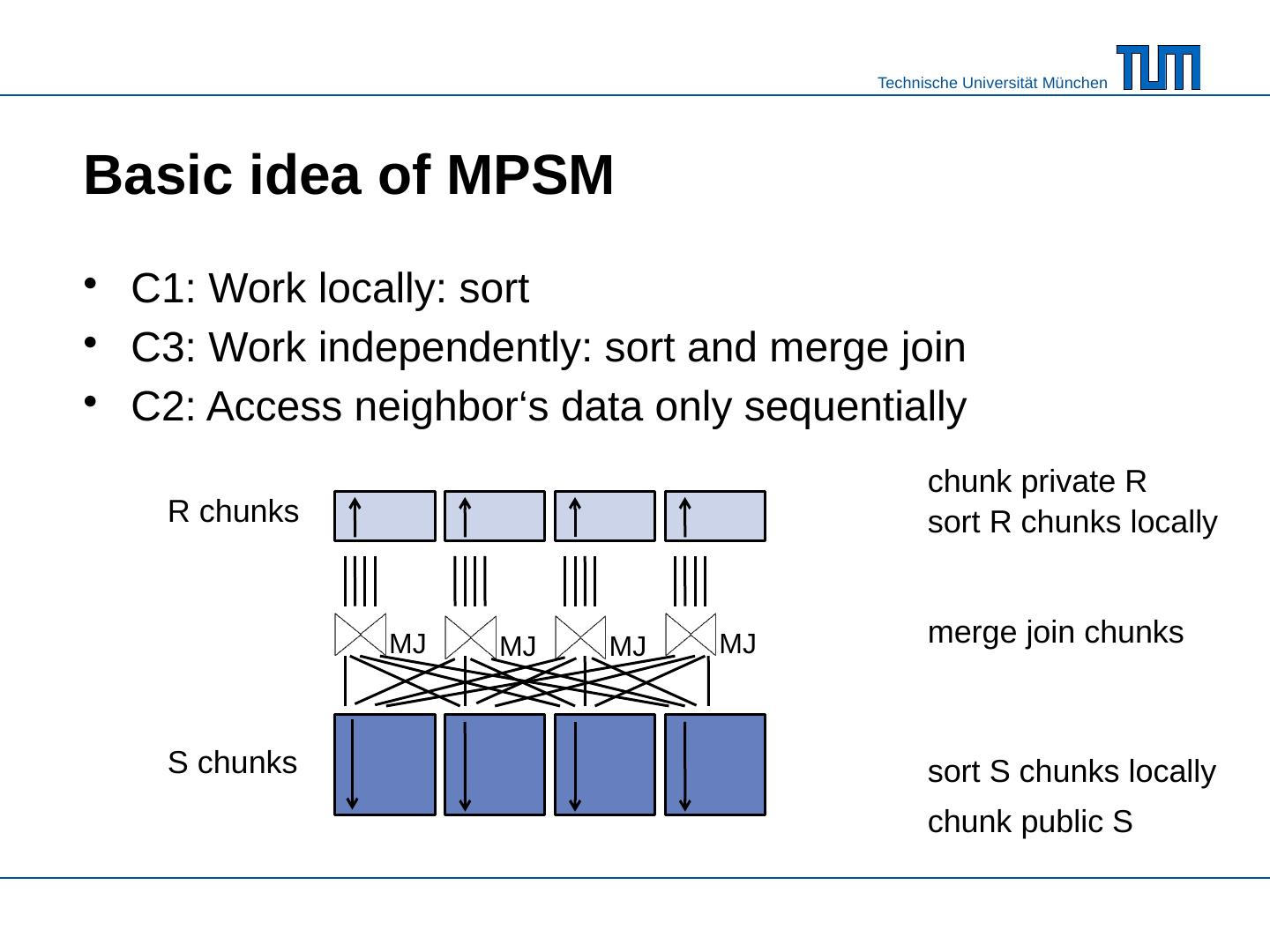
9 .Basic idea of MPSM C1: Work locally : sort C3: Work independently : sort and merge join C2: Access neighbor‘s data only sequentially MJ chunk private R chunk public S sort R chunks locally sort S chunks locally R chunks S chunks merge join chunks MJ MJ MJ

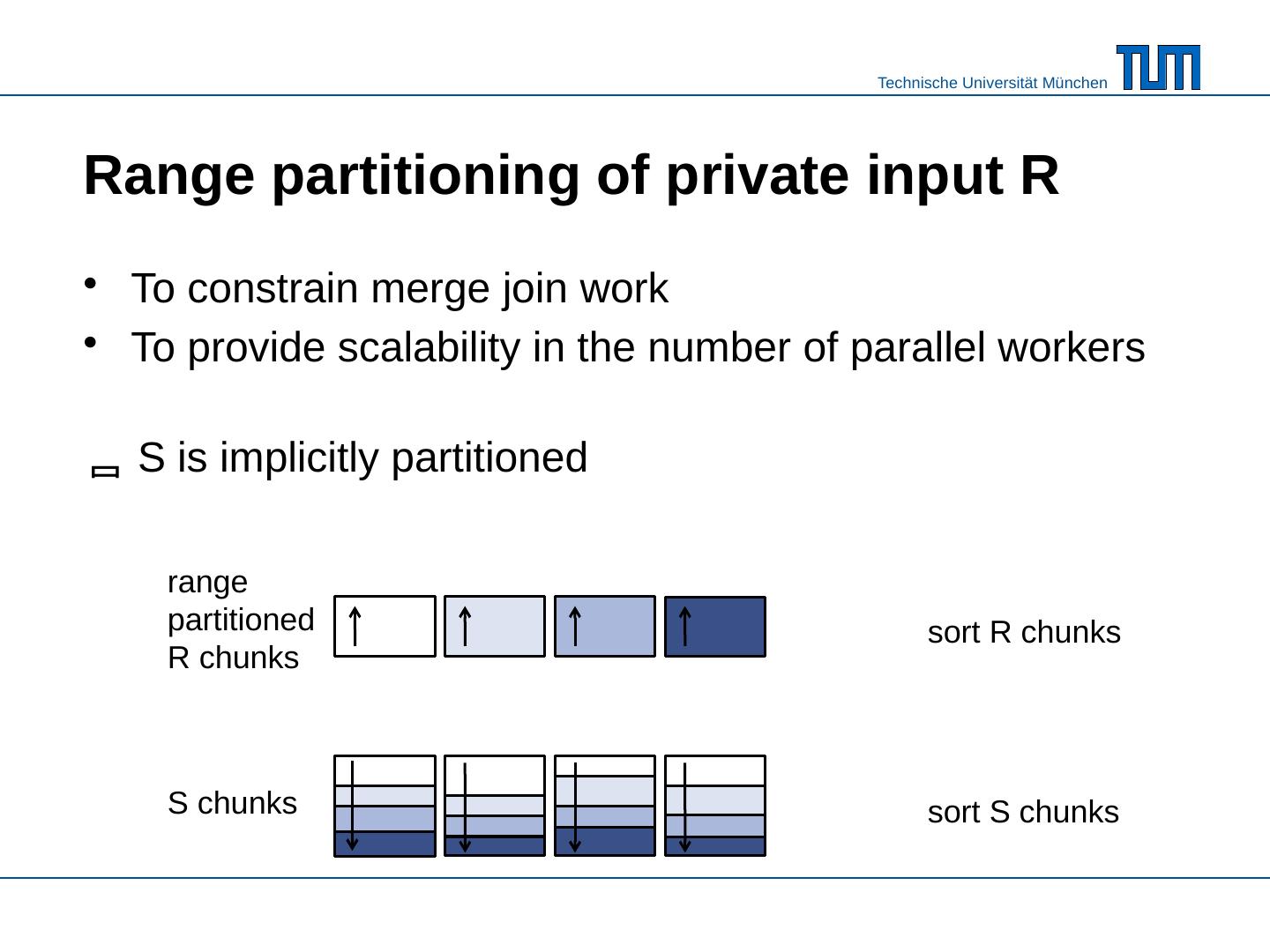
10 .Range partitioning of private input R To constrain merge join work To provide scalability in the number of parallel workers

11 .To constrain merge join work To provide scalability in the number of parallel workers Range partitioning of private input R R chunks range partition R range partitioned R chunks

12 .To constrain merge join work To provide scalability in the number of parallel workers  S is implicitly partitioned Range partitioning of private input R range partitioned R chunks sort R chunks sort S chunks S chunks

13 .To constrain merge join work To provide scalability in the number of parallel workers  S is implicitly partitioned Range partitioning of private input R range partitioned R chunks sort R chunks sort S chunks S chunks MJ MJ MJ MJ merge join only relevant parts

14 .Range partitioning of private input R Time efficient branch-free comparison-free synchronization-free and Space efficient  densely packed in- place by using radix-clustering and precomputed target partitions to scatter data to

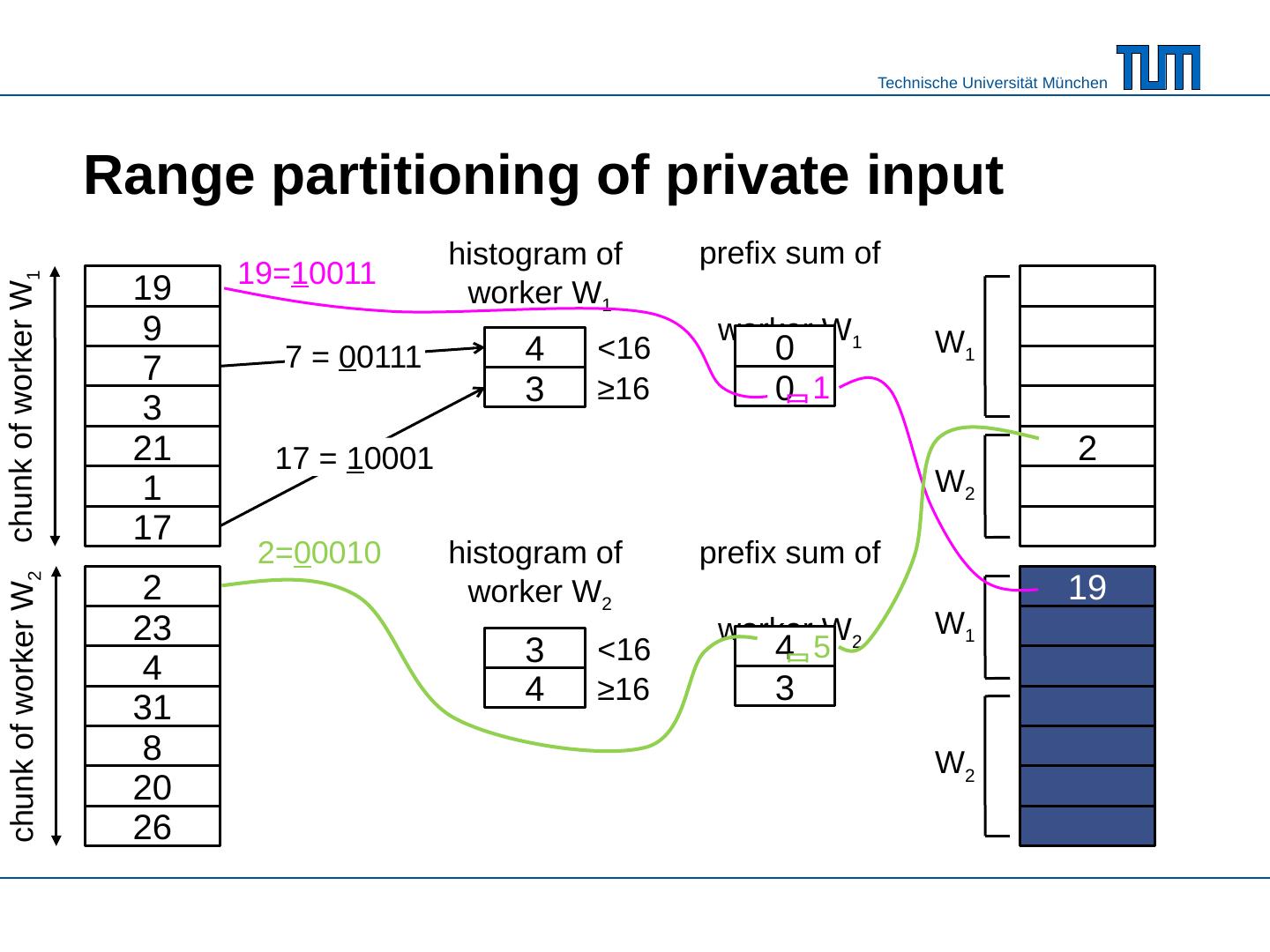
15 .Range partitioning of private input 9 19 7 19 3 21 1 17 2 23 4 31 8 20 26 21 17 23 31 20 26 chunk of worker W 1 chunk of worker W 2 histogram of worker W 1 7 = 0 0111 <16 ≥ 16 17 = 1 0001 histogram of worker W 2 <16 ≥ 16 4 3 3 4 prefix sum of worker W 1 0 0 prefix sum of worker W 2 4 3 W 1 W 2 W 1 W 2  1 19 19= 1 0011  5 2= 0 0010 2

16 .Range partitioning of private input 9 19 7 3 21 1 17 2 23 4 31 8 20 26 chunk of worker W 1 chunk of worker W 2 histogram of worker W 1 7 = 0 0111 <16 17 = 1 0001 histogram of worker W 2 <16 4 3 3 4 prefix sum of worker W 1 0 0 prefix sum of worker W 2 4 3 7 3 9 1 4 17 31 2 8 21 23 20 26 W 1 W 2 W 1 W 2  1 19 19= 1 0011 ≥ 16 ≥ 16  5 2= 0 0010

17 .21 19 Location skew is implicitly handled Distribution skew Dynamically computed partition bounds Determined based on the global data distributions of R and S Cost balancing for sorting R and joining R and S Skew resilience of MPSM 2 1 3 5 7 10 20 2 4 5 8 10 13 24 25 28 S 1 S 2 13 4 2 31 20 8 6 31 20 R 1 20 25 24 28 9 19 7 3 21 1 17 7 R 2

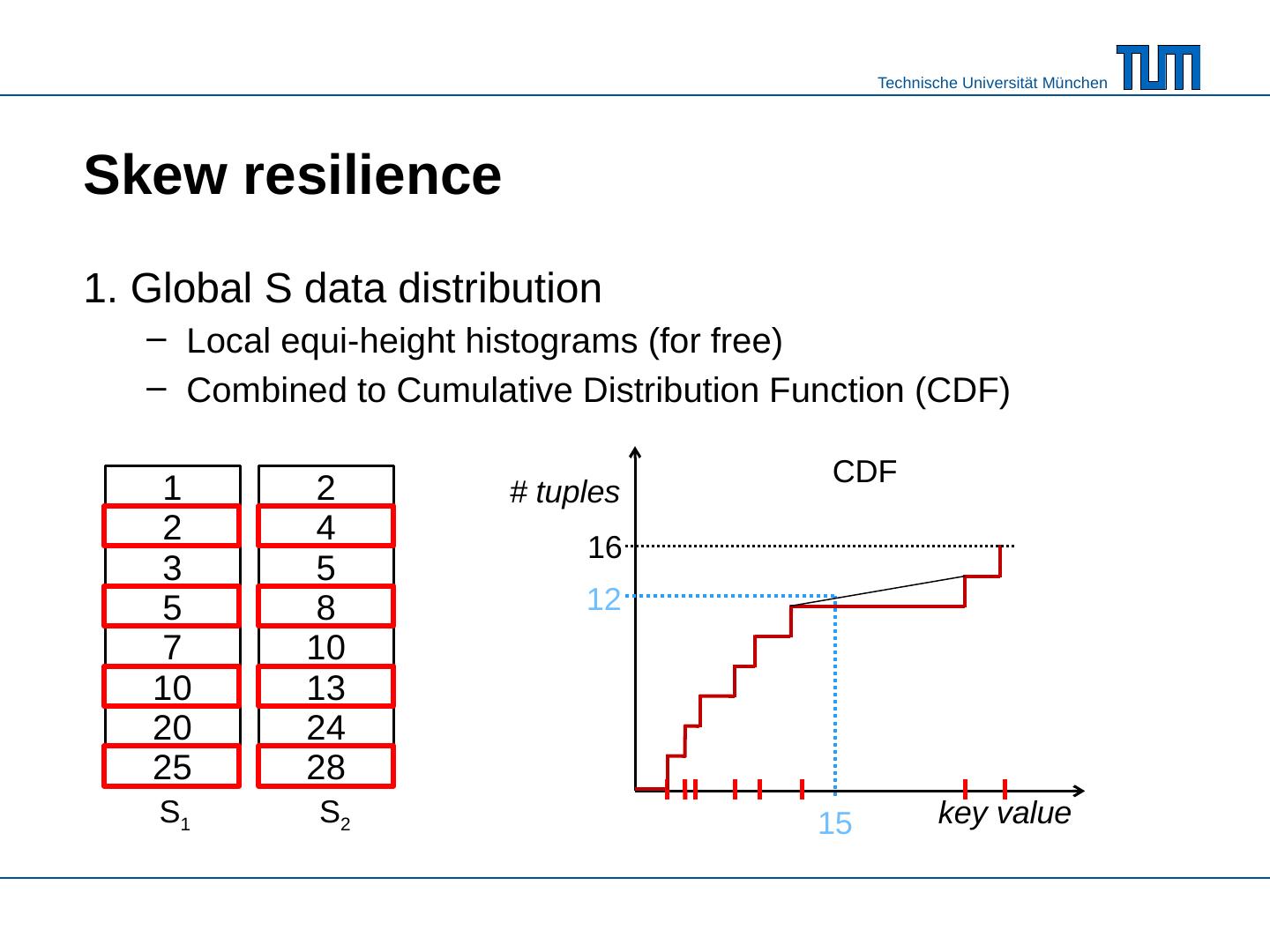
18 .Skew resilience 1. Global S data distribution Local equi-height histograms ( for free ) Combined to Cumulative Distribution Function (CDF) 2 1 3 5 7 10 20 2 4 5 8 10 13 24 25 28 S 1 S 2 # tuples key value CDF 15 16 12

19 .Skew resilience 2. Global R data distribution Local equi-width histograms as before More fine-grained histograms 13 4 2 31 20 8 6 histogram <8 [8,16) [16,24) ≥ 24 13 8 31 3 2 1 1 8 = 01 000 2 = 00 010 20 R 1 20

20 .Skew resilience 3. Compute splitters so that overall workloads are balanced *: greedily combine buckets , thereby balancing the costs of each thread for sorting R and joining R and S are balanced # tuples key value CDF histogram 3 2 1 1 + = 4 2 6 13 8 20 31 * Ross and Cieslewicz : Optimal Splitters for Database Partitioning with Size Bounds . ICDT‘09

21 .Performance evaluation MPSM performance in a nutshell : 160 mio records joined per second 27 bio records joined in less than 3 minutes scales linearly with the number of cores Platform : Linux server 1 TB RAM 32 cores Benchmark: Join tables R and S with schema {[ joinkey : 64bit, payload : 64bit]} Dataset sizes ranging from 50GB to 400GB

22 .Execution time comparison MPSM, Vectorwise (VW), and Blanas hash join * 32 workers |R| = 1600 mio (25 GB), varying size of S * S. Blanas , Y. Li, and J. M. Patel: Design and Evaluation of Main Memory Hash Join Algorithms for Multi- core CPUs. SIGMOD 2011

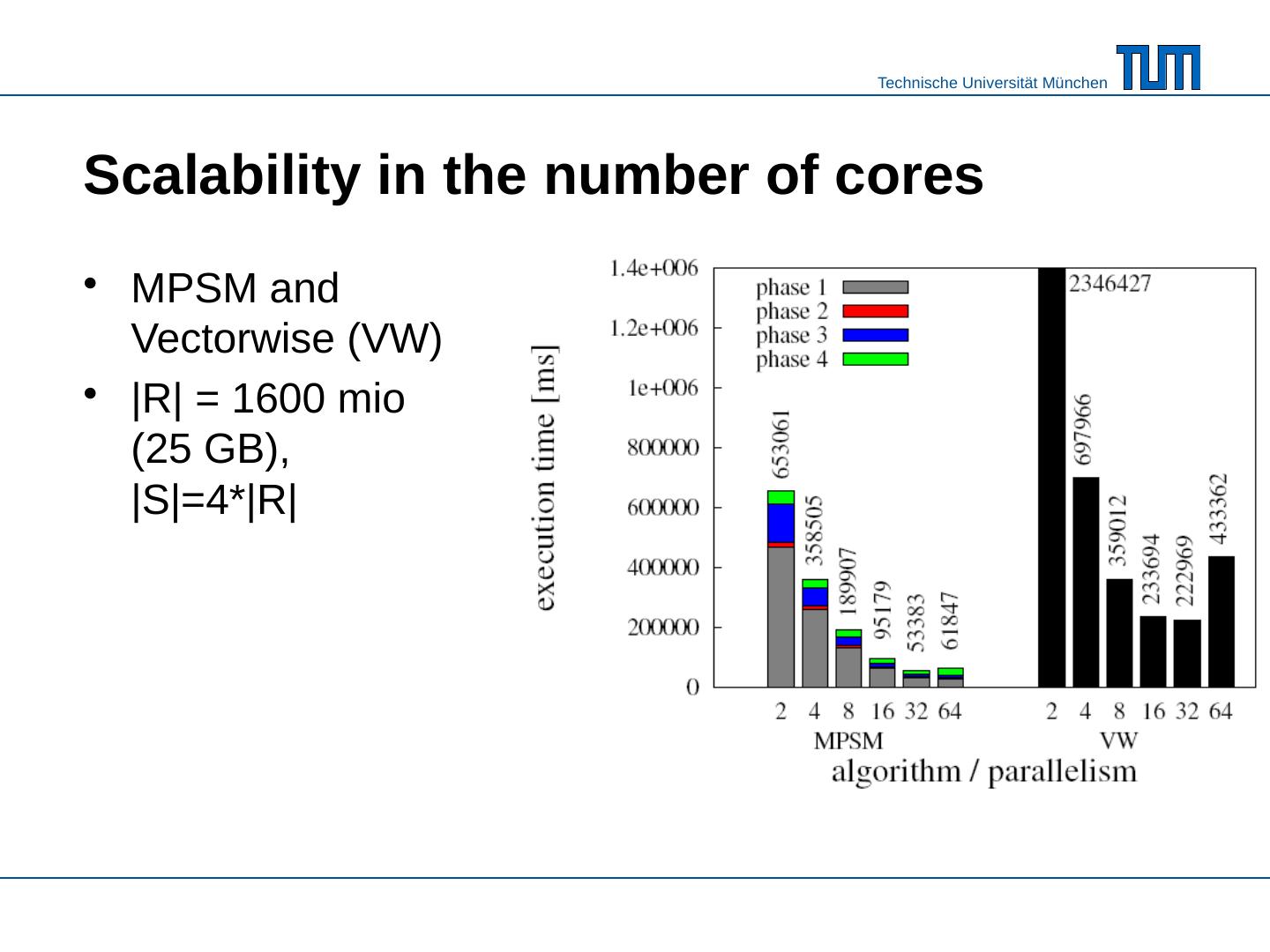
23 .Scalability in the number of cores MPSM and Vectorwise (VW) |R| = 1600 mio (25 GB), |S|=4*|R|

24 .Location skew Location skew in R has no effect because of repartitioning Location skew in S: in the extreme case all join partners of R i are found in only one S j ( either local or remote)

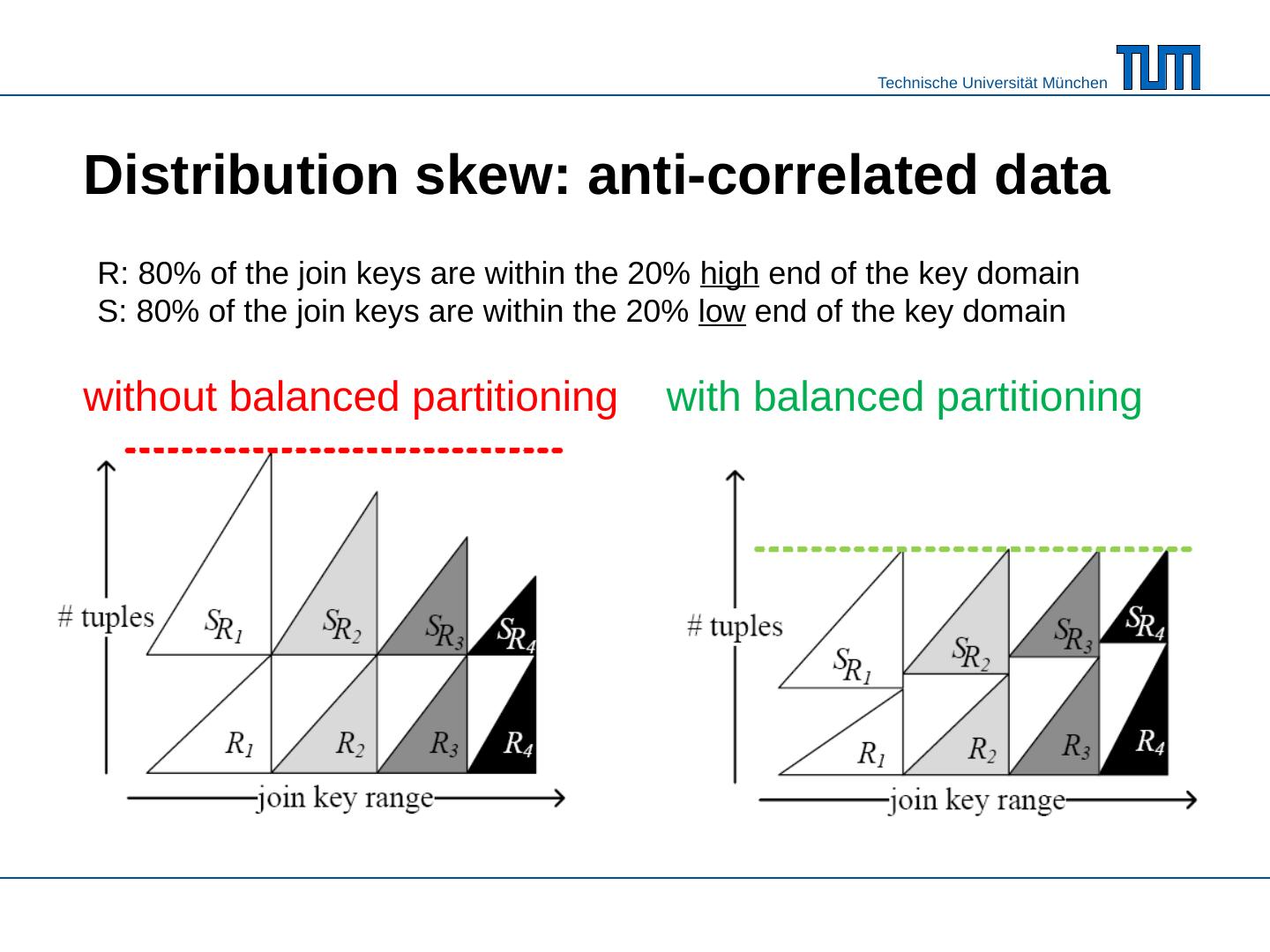
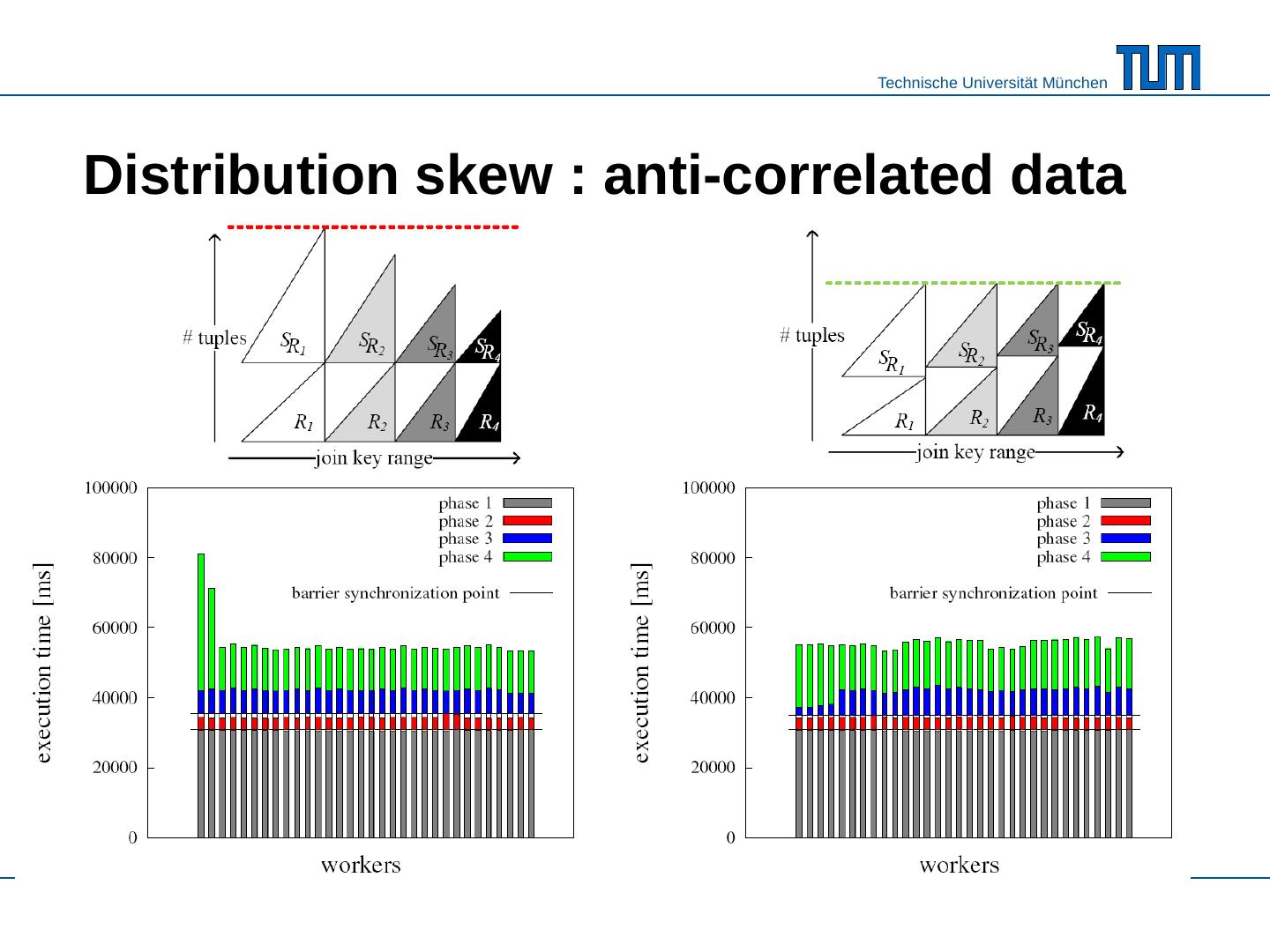
25 .Distribution skew : anti- correlated data without balanced partitioning with balanced partitioning R: 80% of the join keys are within the 20% high end of the key domain S: 80% of the join keys are within the 20% low end of the key domain

26 .Distribution skew : anti- correlated data

27 .Conclusions MPSM is a sort-based parallel join algorithm MPSM is NUMA- aware & NUMA- oblivious MPSM is space efficient ( works in- place ) MPSM scales linearly in the number of cores MPSM is skew resilient MPSM outperforms Vectorwise (4X) and Blanas et al.‘s hash join (18X) MPSM is adaptable for disk-based processing See details in paper

28 .Massively Parallel Sort-Merge Joins (MPSM) in Main Memory Multi-Core Database Systems Martina Albutiu, Alfons Kemper, and Thomas Neumann Technische Universität München THANK YOU FOR YOUR ATTENTION!