- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
高性能计算与天文学
展开查看详情
1 .2018/6/6 1 并行计算
2 .第十章 线性方程组的求解 10.1 三角形方程组的求解 10.2 三对角方程组的求解 10.3 稠密线性方程组的求解 10.4 稀疏线性方程组的求解 2018/6/6 2
3 .10.1 三角形方程组的求解 10.1.1 基本术语 10.1.2 上三角方程组的求解 2018/6/6 3
4 . 基本术语 2018/6/6 4 线性方程组的定义和符号 a 1,1 x 1 + a 1,2 x 2 + … + a 1,n x n = b 1 a 2,1 x 1 + a 2,1 x 2 + … + a 2,n x n = b 2 a n,1 x 1 + a n,1 x 2 + … + a n,n x n = b n 记为 AX=b
5 .10.1 三角形方程组的求解 10.1.1 基本术语 10.1.2 上三角方程组的求解 2018/6/6 5
6 .上三角方程组的回代解法并行化 (1)SISD 上的回代算法 Begin (1)for i =n downto 1 do (1.1)x i =b i / a ii (1.2)for j=1 to i-1 do b j = b j -a ji x i a ji =0 endfor endfor End 上三角方程组的求解 2018/6/6 6 可并行化
7 . 上三角方程组的求解 2018/6/6 7 上三角方程组的回代解法并行化 (2)SIMD-CREW 上的并行回代算法 - 划分 : p 个处理器行循环带状划分 - 算法 Begin for i=n downto 1 do x i =b i /a ii for all P j , where 1≤j≤p do for k=j to i-1 step p do b k =b k -a ki x i a ki =0 endfor endfor endfor End // p(n)=n, t(n)=n
8 .第十章 线性方程组的求解 10.1 三角形方程组的求解 10.2 三对角方程组的求解 10.3 稠密线性方程组的求解 10.4 稀疏线性方程组的求解 2018/6/6 8
9 .10.2 三对角方程组的求解 10.2.1 直接求解法 10.2.2 奇偶归约法 2018/6/6 9
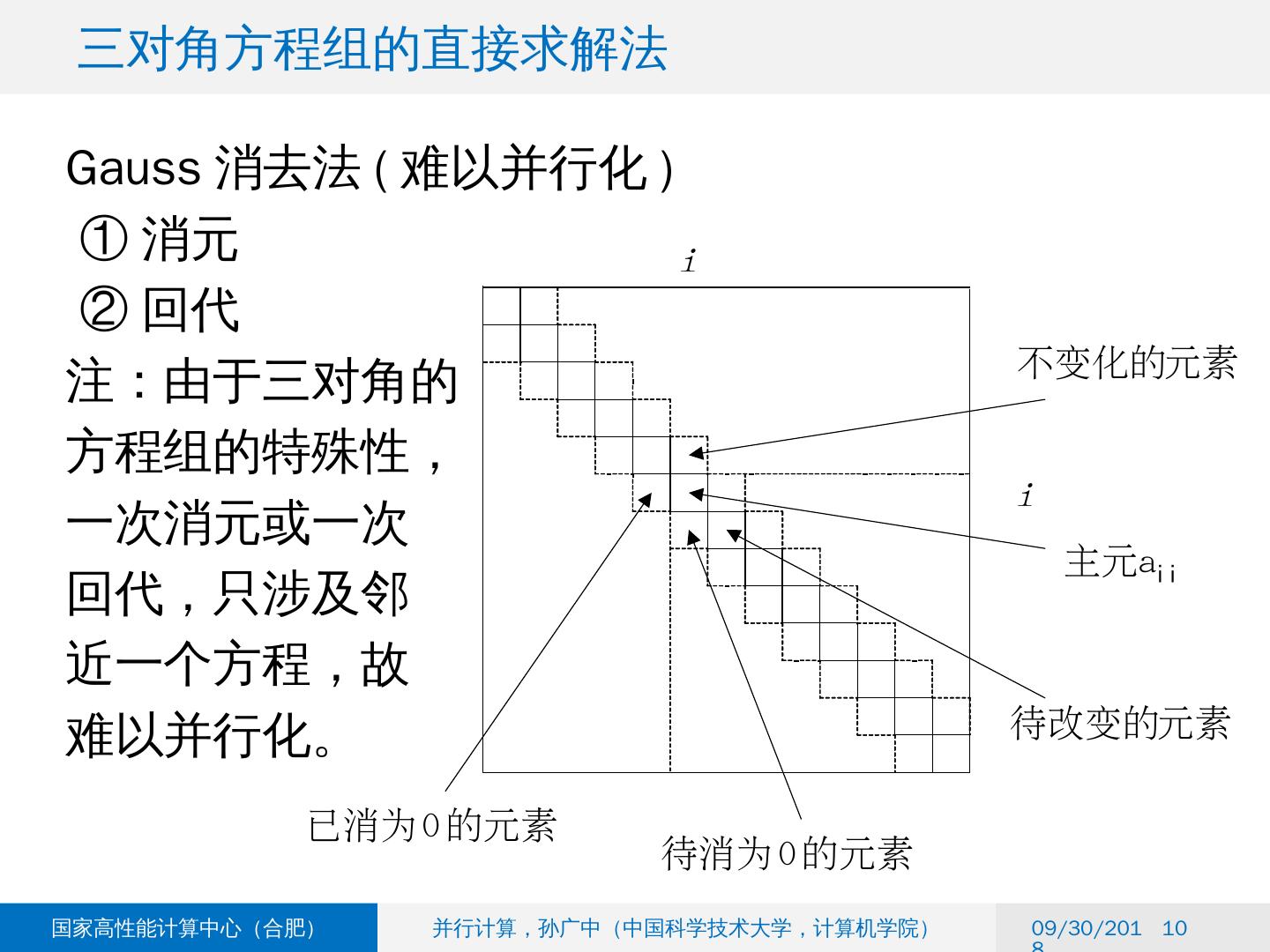
10 . 三对角方程组的直接求解法 2018/6/6 10 Gauss 消去法 ( 难以并行化 ) ① 消元 ② 回代 注:由于三对角的 方程组的特殊性, 一次消元或一次 回代,只涉及邻 近一个方程,故 难以并行化。
11 .10.2 三对角方程组的求解 10.2.1 直接求解法 10.2.2 奇偶归约法 2018/6/6 11
12 . 三对角方程组的奇偶归约法 2018/6/6 12 奇偶归约求解法 ( 可并行化 ) 三对角方程可以写成如下形式 串行算法描述 ① 利用上下相邻方程消去偶序号方程中的奇下标变量 : 方程乘上某个数消去 2i 方程中的 项 , 方程乘上某个数 消去 方程中的 项 , 使 方程变为
13 . 三对角方程组的奇偶归约法 2018/6/6 13 ② 重复 ① 最终可得 : case 1: case 2: 可以分别得到 解得 ③ 回代求解 x 并行化分析 : ① 、 ② 消去奇下标可以并行化; ③ 回代求解可以并行化 PRAM-CREW 上,时间 : 处理器数:
14 .第十章 线性方程组的求解 10.1 三角形方程组的求解 10.2 三对角方程组的求解 10.3 稠密线性方程组的求解 10.4 稀疏线性方程组的求解 2018/6/6 14
15 .10.3 稠密线性方程组的求解 10.3.1 有回代的高斯消去法 10.3.2 无回代的高斯 - 约旦法 10.3.3 迭代求解的高斯 - 赛德尔法 2018/6/6 15
16 . 有回代的高斯消去法 2018/6/6 16 算法基本原理 求解过程分为消元和回代两个阶段,消元是将系数矩阵 A 化为上三角阵 T ,然后对 TX=c 进行回代求解。 消元过程中可以应用选主元方法,增加算法的数值稳定性。 图 10.1 是消元过程图:
17 . 有回代的高斯消去法 2018/6/6 17 并行化分析 消元和回代均可以并行化; 选主元也可以并行化; 消元过程的并行化图示:处理器按行划分
18 .10.3 稠密线性方程组的求解 10.3.1 有回代的高斯消去法 10.3.2 无回代的高斯 - 约旦法 10.3.3 迭代求解的高斯 - 赛德尔法 2018/6/6 18
19 .串行算法原理 ① 消元 : 通过初等行变换 , 将 ( A,b ) 化为主对角线矩阵 , 记 b 为 A 的第 n+1 列 ② 求解 : 无回代的高斯 - 约旦法 2018/6/6 19
20 . 无回代的高斯 - 约旦法 2018/6/6 20 SIMD-CREW 上的并行算法 (1) 处理器 : n×(n+1) 个处理器 , 排成 n×(n+1) 的矩阵 , 处理器编号为 , i =1~n, k=1~n+1 (2) 并行化分析 ① 消元的并行化 : // O(n) for j=1 to n-1, each Par-do // 第 j 次消元 ( i <>j): <— 0 ( i <>j, k=j+1~n+1 ): <— - end for ② 求解 : for each (j=1~n) Par-do: <— , //O(1) (3) 时间分析 : t(n)=O(n), p(n)=O( n 2 ), c(n)=O( n 3 ) 成本最优?
21 .成本最优? 串行算法的最优时间: 由于 x=A -1 b ①A -1 b( 假设已有 A -1 ): O(n 2 ) ② 求 A -1 : ∴ 求 A -1 需要 : 2 次 n/2×n/2 矩阵的逆 i (n/2) 6 次 n/2×n/2 矩阵的乘 m(n/2) 2 次 n/2×n/2 矩阵的加 a(n/2) i (n)= i (n/2)+6m(n/2)+2a(n/2) a(n/2)=n 2 /2, m(n/2)=O((n/2) x ) 2<x<2.5 => i (n)=O( n x ) 综上,串行算法的最优时间为 O( n x ) 2<x<2.5 无回代的高斯 - 约旦法 2018/6/6 21
22 .10.3 稠密线性方程组的求解 10.3.1 有回代的高斯消去法 10.3.2 无回代的高斯 - 约旦法 10.3.3 迭代求解的高斯 - 赛德尔法 2018/6/6 22
23 .迭代求解的高斯 - 赛德尔法 2018/6/6 23 串行算法原理 如果对某个 k, 给定的误差允许值 c 有 则认为迭代是收敛的。 并行化分析 由于每次迭代需要使用本次迭代的前面部分值,因而难以到同步的并行算法,下面给出一个异步的并行算法
24 .迭代求解的高斯 - 赛德尔法 2018/6/6 24 MIMD 异步并行算法 N 个处理器 ( N≤n ) 生成 n 个进程 , 每个进程计算 x 的一个分量 Begin ( (2) 生成进程 i (3) 进程 i repeat ( i ) (ii) until End
25 .第十章 线性方程组的求解 10.1 三角形方程组的求解 10.2 三对角方程组的求解 10.3 稠密线性方程组的求解 10.4 稀疏线性方程组的求解 2018/6/6 25
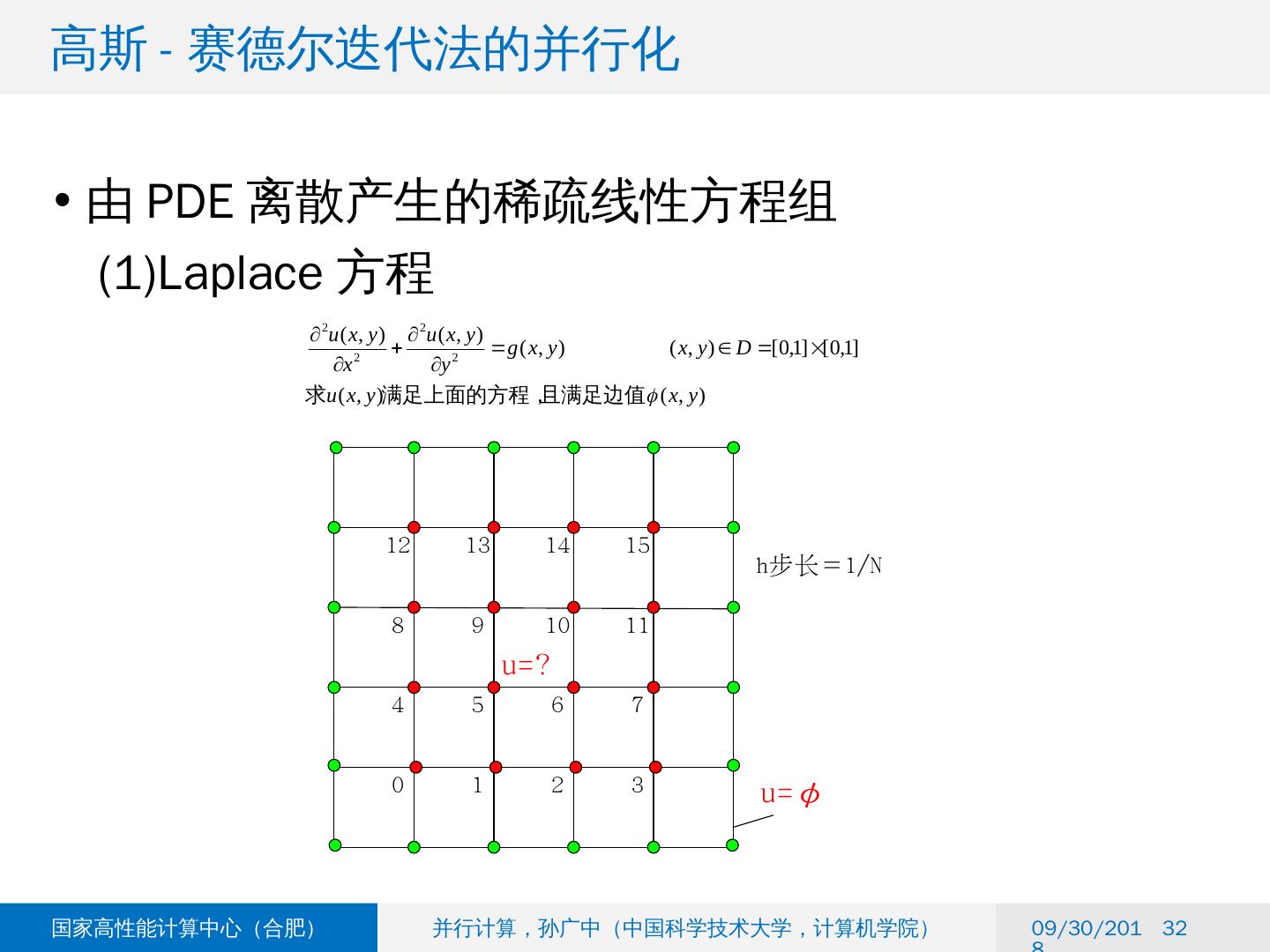
26 .10.4 稀疏线性方程组的求解 10.4.1 线性方程组的并行化方法 10.4.2 稀疏线性方程组的迭代解法 10.4.3 高斯 - 赛德尔迭代法的并行化 2018/6/6 26
27 .线性方程方程的并行化方法 2018/6/6 27 线性方程组选择算法的考虑因素 系数矩阵 A 的结构 dense Gaussian elimination, etc Sparse iterative method triangular substitution, odd-even reduction certain PDEs multigrid, etc 计算精度要求 Gaussian elimination: more accurate, more expensive Conjugate gradients: less accurate, less expensive 计算环境要求 architecture, available languages, compiler quality libraries?
28 .线性方程方程的并行化方法 2018/6/6 28 求解方法的并行化 (1) 直接解法的并行化 ( 用于稠密线性方程组 ) - Gauss 消去法 ( 包括选主元的 Gauss 消去法 ) - Gauss-Jordan 消去法 - LU 分解法 (2) 迭代法的并行化 ( 用于稠密和稀疏线性方程组 ) - Jacobi - Gauss-Seidel( 可异步并行化 ) - Jacobi OverRelaxation(JOR) - Gauss-Seidel OverRelaxation(SOR) - Conjugate Gradient
29 .10.4 稀疏线性方程组的求解 10.4.1 线性方程组的并行化方法 10.4.2 稀疏线性方程组的迭代解法 10.4.3 高斯 - 赛德尔迭代法的并行化 2018/6/6 29