展开查看详情
1 .—— 从信号的角度 傅里叶变换的推导 计算机科学与工程学院 李华繁 ( Takashi) 2015,10
2 .傅里叶变换就是傅里叶级数当周期趋向于无穷大的形式。 完结撒花。。。
3 .Outline 线性时不变系统 傅里叶级数 傅里叶变换
4 .线性时不变系统 信号的表示 LTI 系统 信号通过 LTI 系统
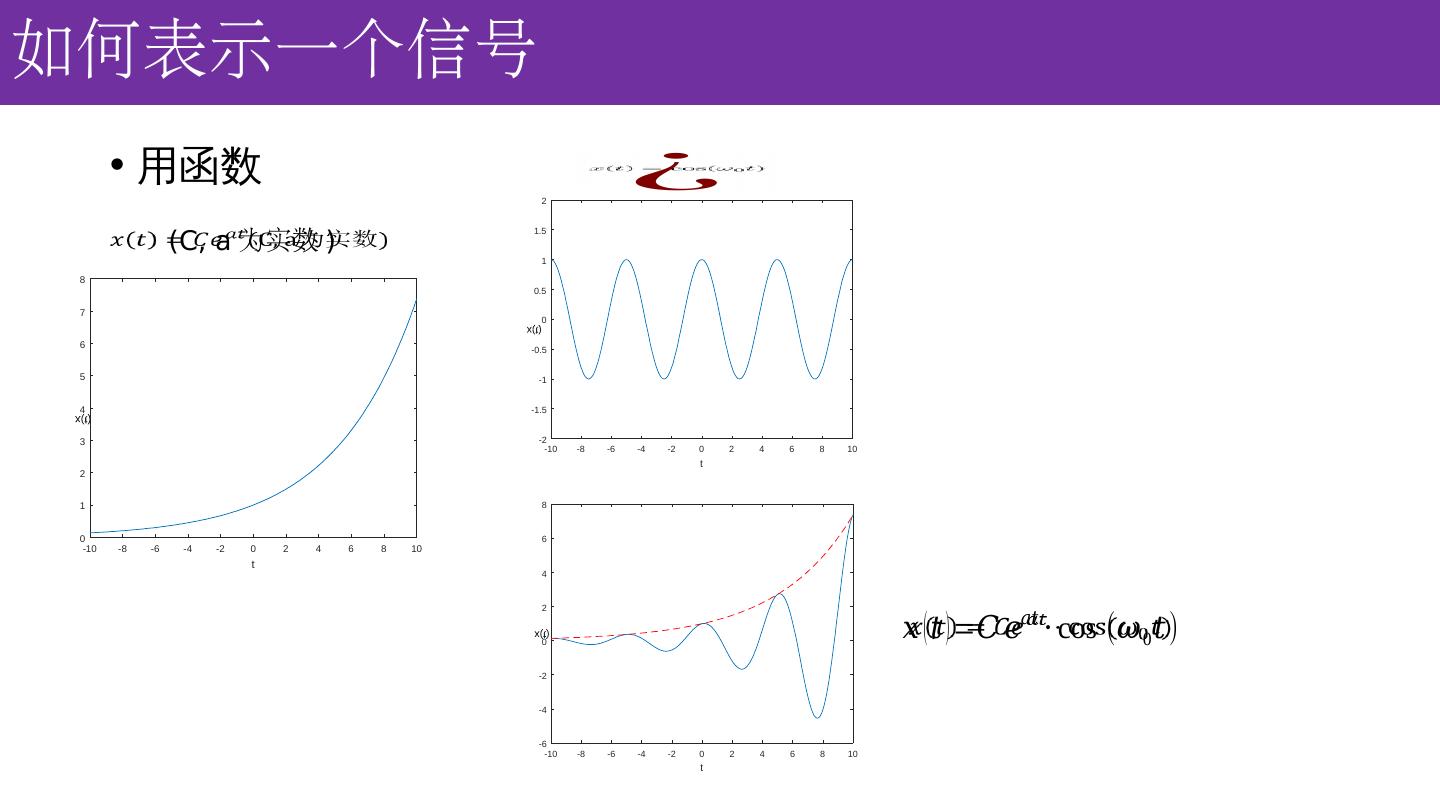
5 .如何表示一个信号 用函数 (C, a 为实数 )
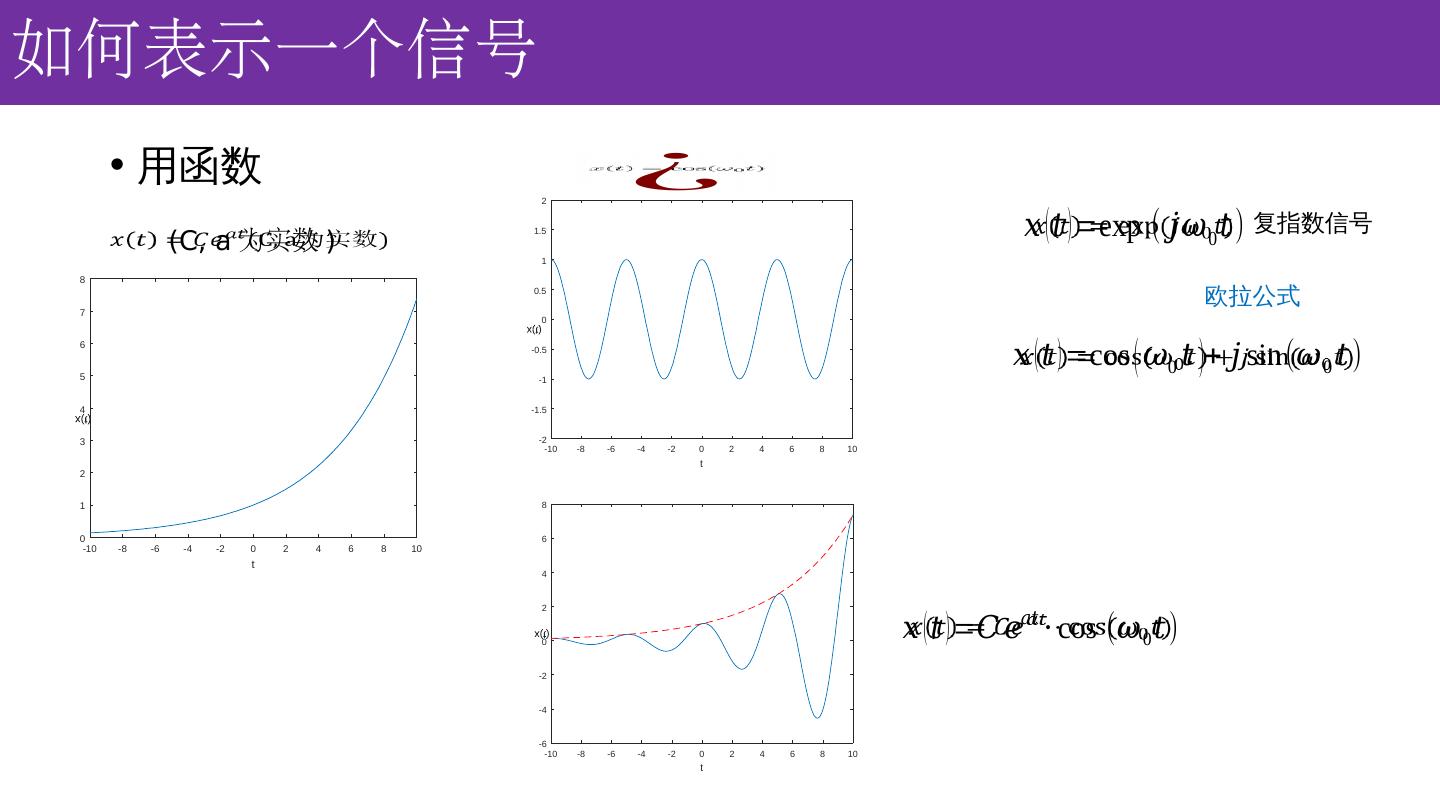
6 .如何表示一个信号 用函数 欧拉公式 (C, a 为实数 ) 复指数信号
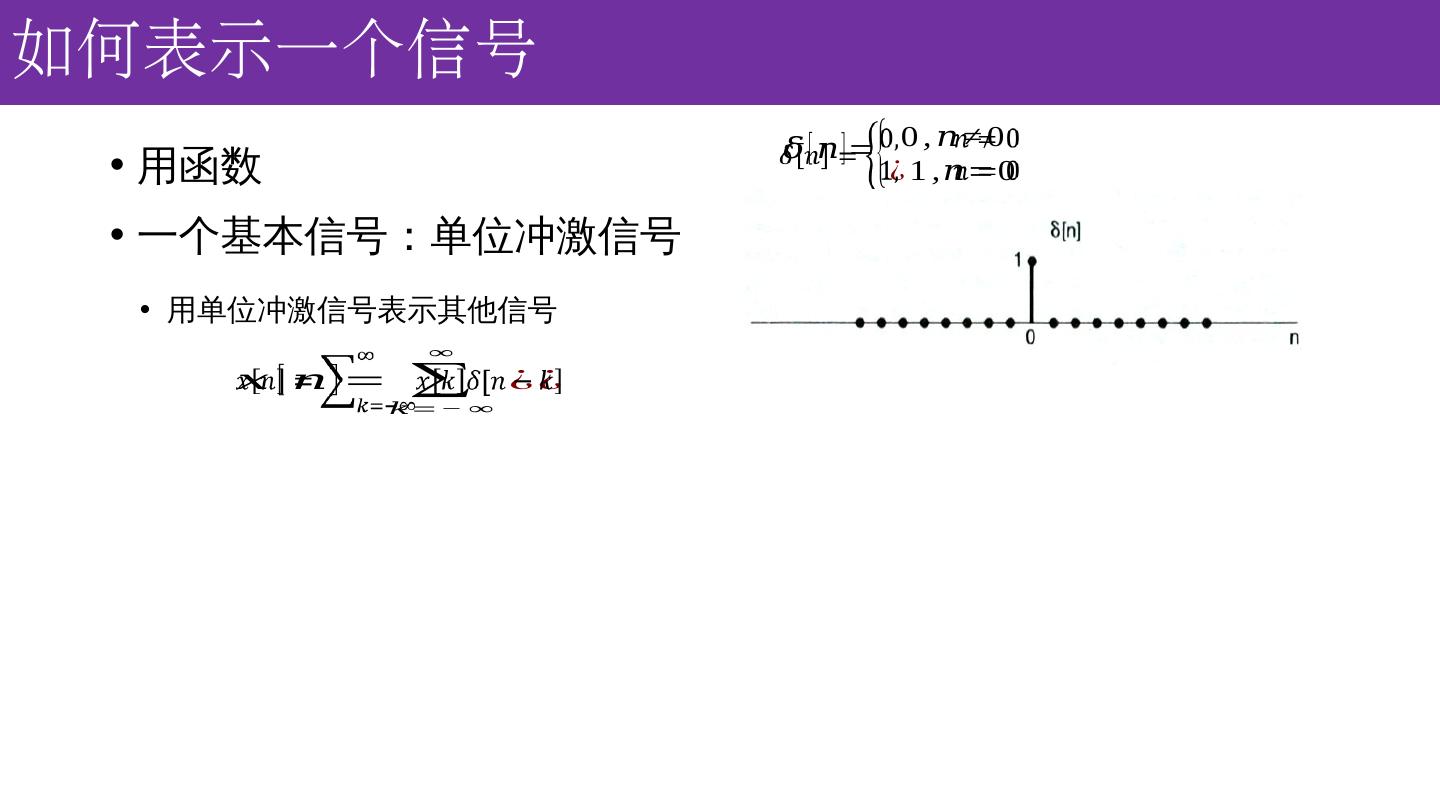
7 .如何表示一个信号 一 个基本信号：单位冲激信号 用函数 用单位冲激信号表示其他信号
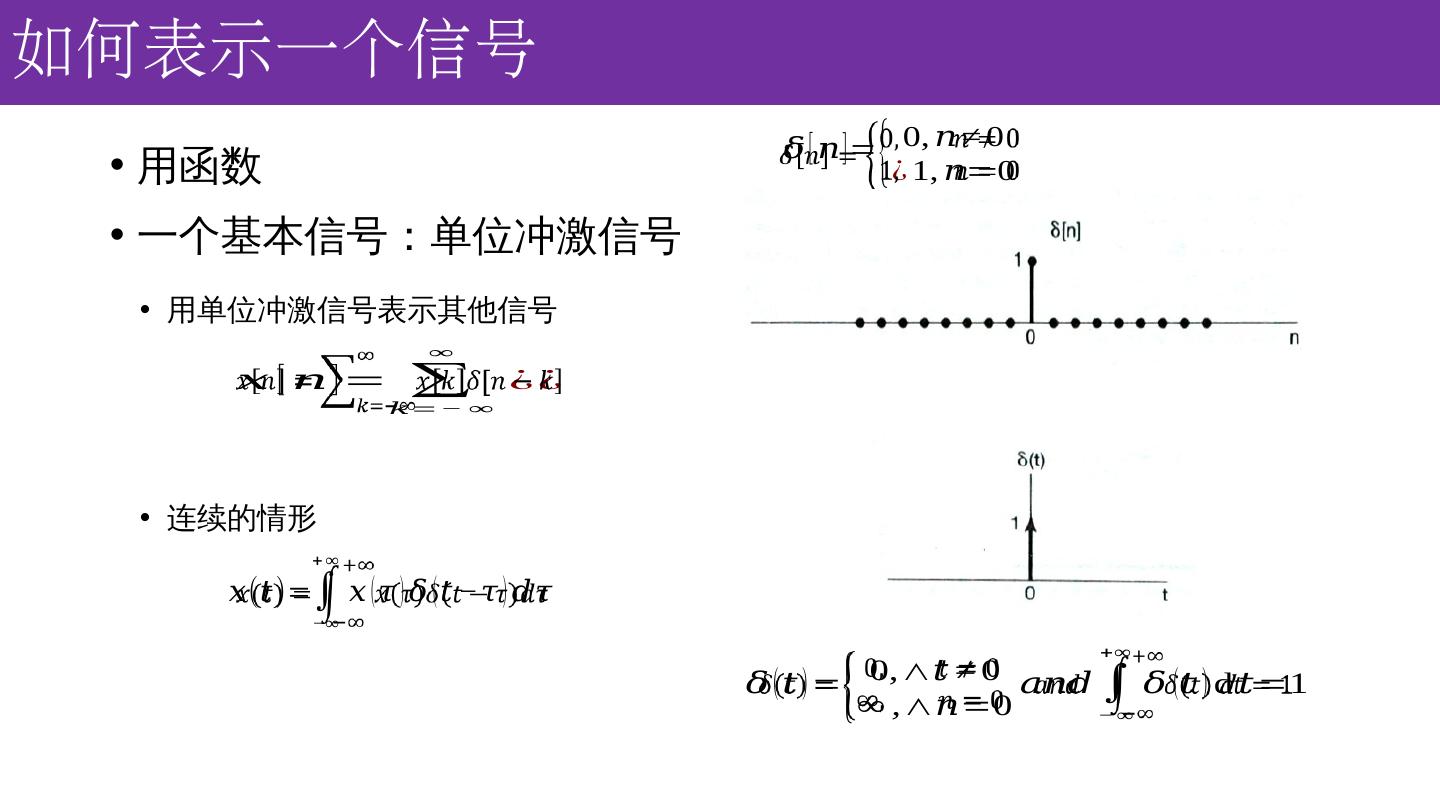
8 .如何表示一个信号 一 个基本信号：单位冲激信号 用函数 用单位冲激信号表示其他信号 连续的情形
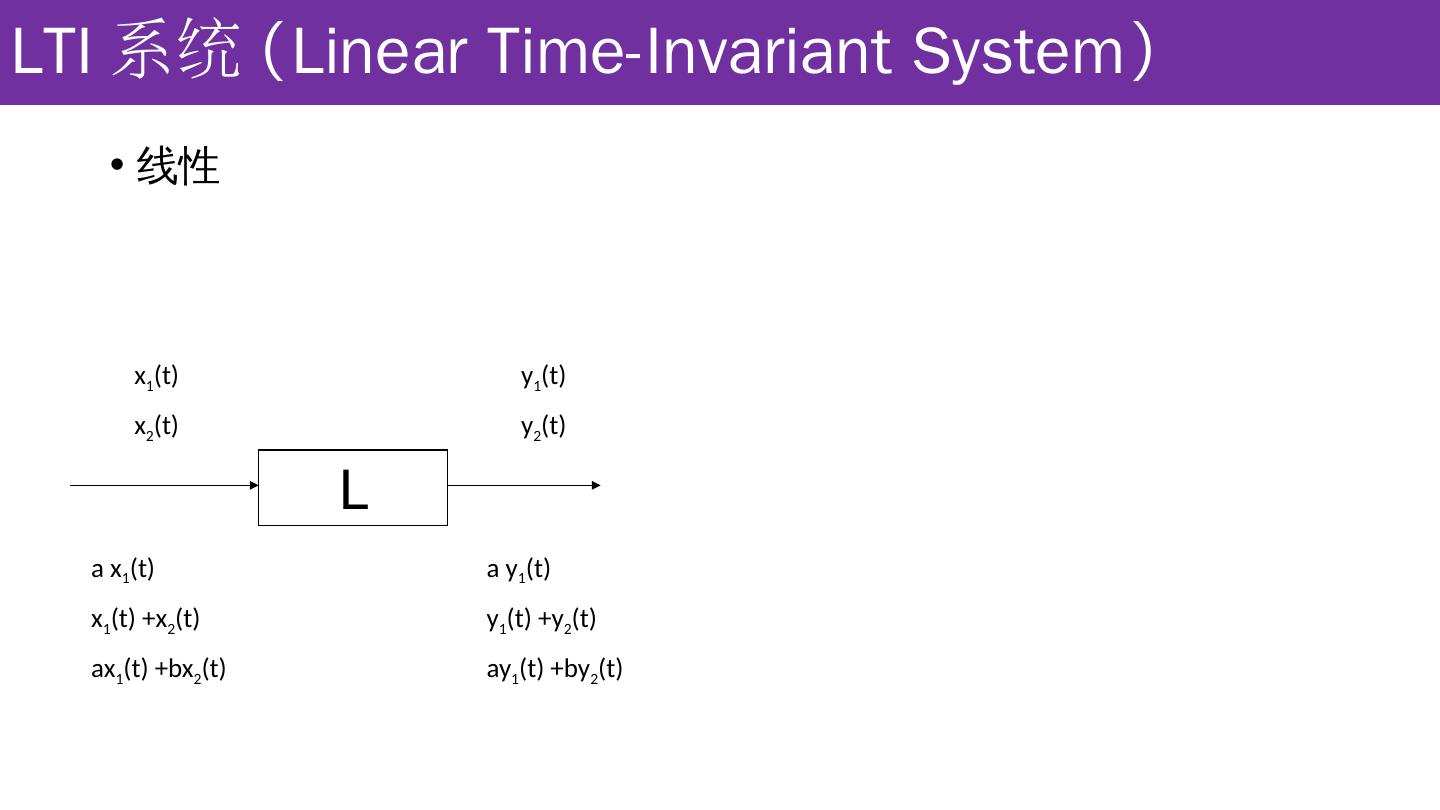
9 .LTI 系统 ( Linear Time-Invariant System ) 线性 L x 1 (t) x 2 (t) y 1 (t) y 2 (t) a x 1 (t) x 1 (t) +x 2 (t) ax 1 (t) +bx 2 (t) a y 1 (t) y 1 (t) +y 2 (t) ay 1 (t) +by 2 (t)
10 .LTI 系统 ( Linear Time-Invariant System ) TI x(t) y(t) x(t-t 0 ) y(t-t 0 ) 线性 时不变性 L x 1 (t) x 2 (t) y 1 (t) y 2 (t) a x 1 (t) x 1 (t) +x 2 (t) ax 1 (t) +bx 2 (t) a y 1 (t) y 1 (t) +y 2 (t) ay 1 (t) +by 2 (t)
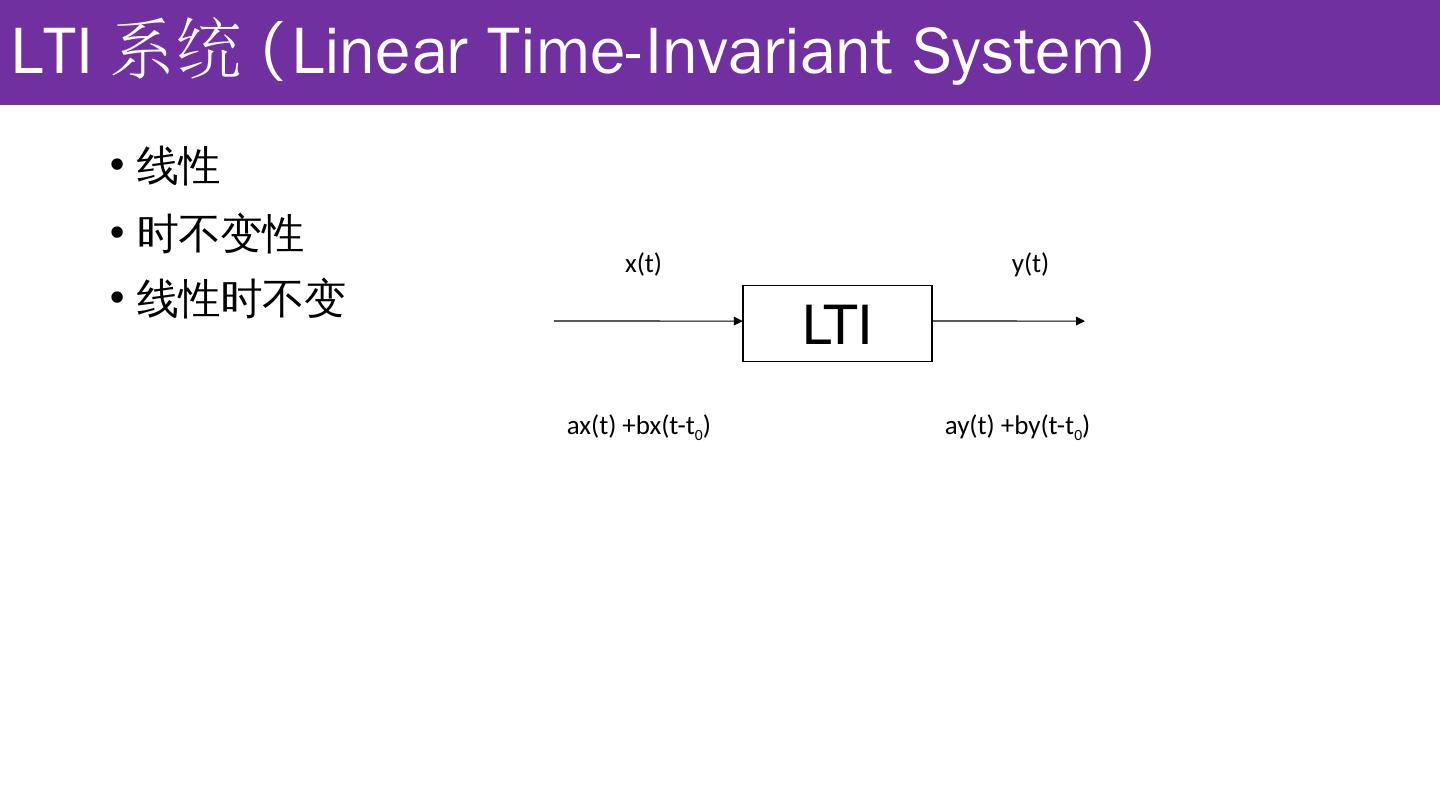
11 .LTI 系统 ( Linear Time-Invariant System ) 线性 时不变性 线性时不变 LTI x(t) y(t) ax(t ) + bx (t-t 0 ) ay(t ) +by(t-t 0 )
12 .当信号通过 LTI 系统 … 当 x[n]= δ [n] 时，输出的 y[n] 叫做系统的单位冲激响应 LTI x[n] y[n] 系统对 x[n] 的响应 通常， 用符号 h[n] 表示系统的单位冲激响应
13 .当信号通过 LTI 系统 … 当 x[n]= δ [n] 时，输出的 y[n] 叫做系统的单位冲激响应 LTI x[n] y[n] 系统对 x[n] 的响应 如果 x[n] 更复杂一点？ 通常， 用符号 h[n] 表示系统的单位冲激响应
14 .当信号通过 LTI 系统 … 当 x[n]= δ [n] 时，输出的 y[n] 叫做系统的单位冲激响应 LTI x[n] y[n] 系统对 x[n] 的响应 如果 x[n] 更复杂一点？ 通常， 用符号 h[n] 表示 系统的单位冲激响应 [n] h[n] [n-k] h[n-k] x[k][n-k] x[k] h[n-k]
15 .当信号通过 LTI 系统 … 当 x[n]= δ [n] 时，输出的 y[n] 叫做系统的单位冲激响应 LTI x[n] y[n] 系统对 x[n] 的响应 如果 x[n] 更复杂一点？ 通常， 用符号 h[n] 表示 系统的单位冲激响应 [n] h[n] [n-k] h[n-k] x[k][n-k] x[k] h[n-k]
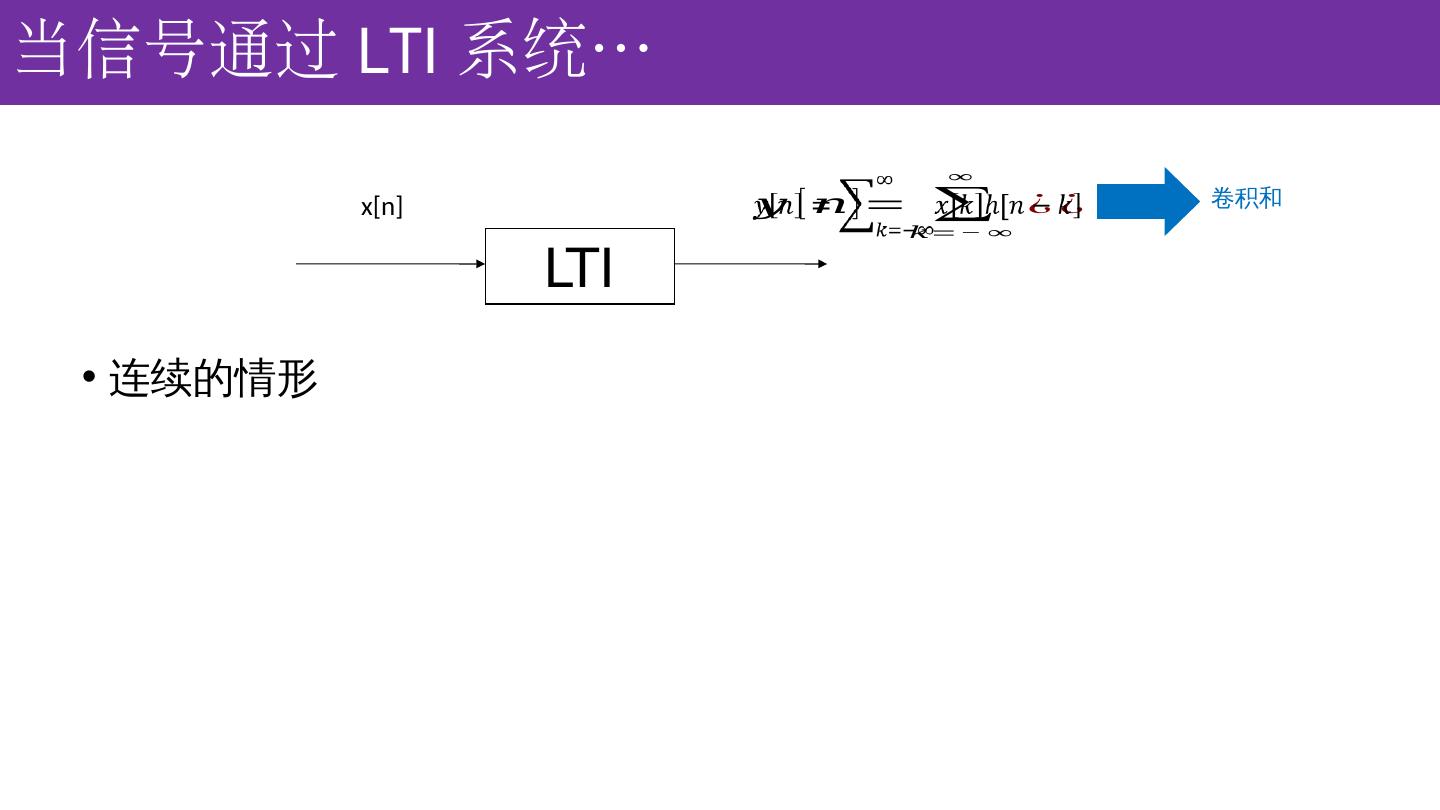
16 .当信号通过 LTI 系统 … 连续的情形 LTI x[n] 卷积和
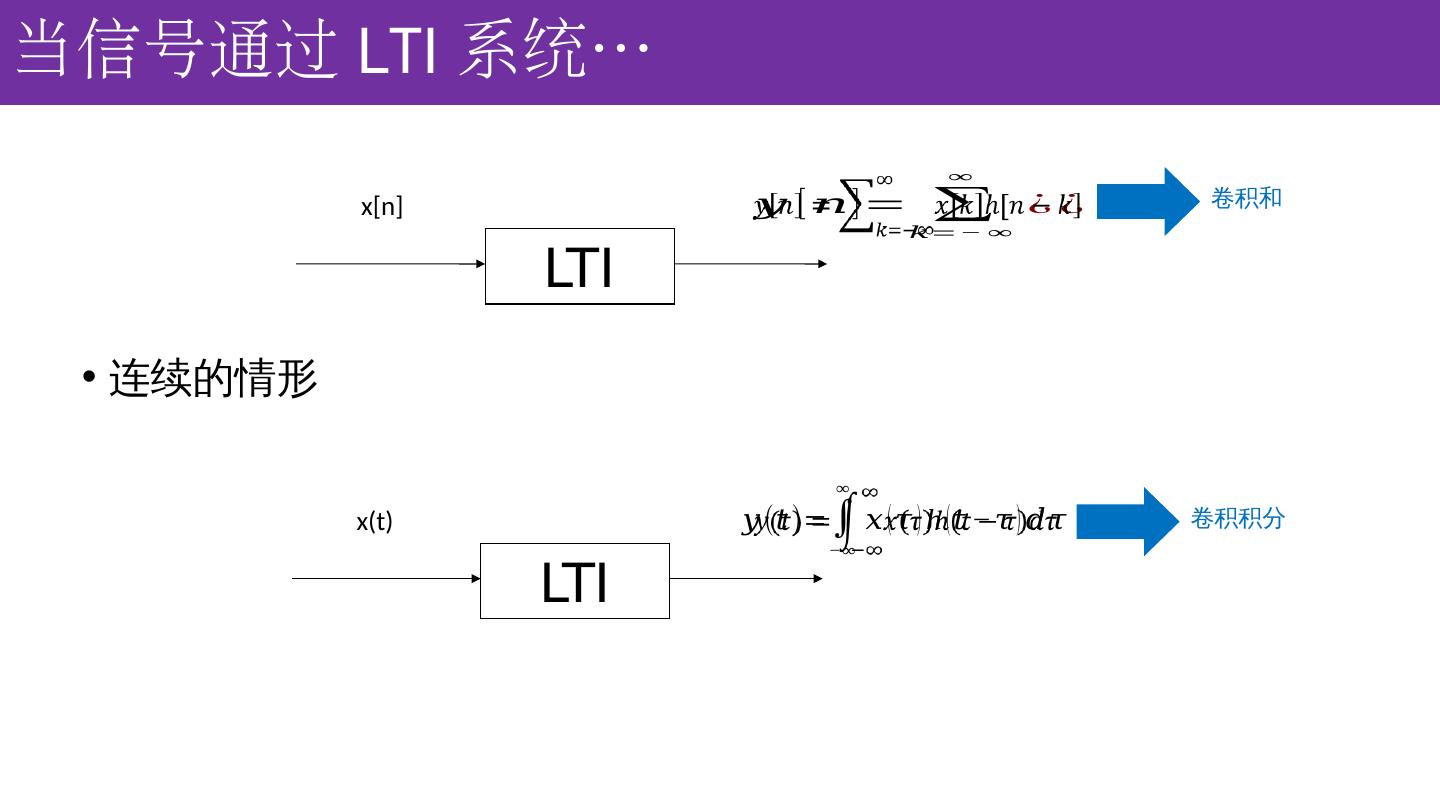
17 .当信号通过 LTI 系统 … 连续的情形 LTI x[n] 卷积和 LTI x(t) 卷积 积分
18 .现在我们来谈谈信号的展开 信号的 展开 信号的傅里叶级数
19 .信号展开 … 似曾相识 ？ 任何一个函数可以分解为一个奇函数和偶函数之和 泰 勒展开 - 将复杂的函数表示成幂级数的线性叠加 - 复杂的函数可以用多项式来表示了啊啊！ 二维平面的任何曲线运动可以分解为两个正交方向上的直线运动 三维空间的任何曲线运动可以分解为三个正交方向上的直线运动
20 .那些年，我们展开过的函数 在它们的基础上可以进一步导出欧拉公式 以及上帝创造的等式 —
21 .信号展开 … 似曾相识 ？ 任何一个函数可以分解为一个奇函数和偶函数之和 泰 勒展开 - 将复杂的函数表示成幂级数的线性叠加 - 复杂的函数可以用多项式来表示了啊啊！ 二维平面的任何曲线运动可以分解为两个正交方向上的直线运动 三维 空间 的任何曲线运动可以分解为三个正交方向上的直线运动 有没有其他的式子（级数）可以用来对信号展开？
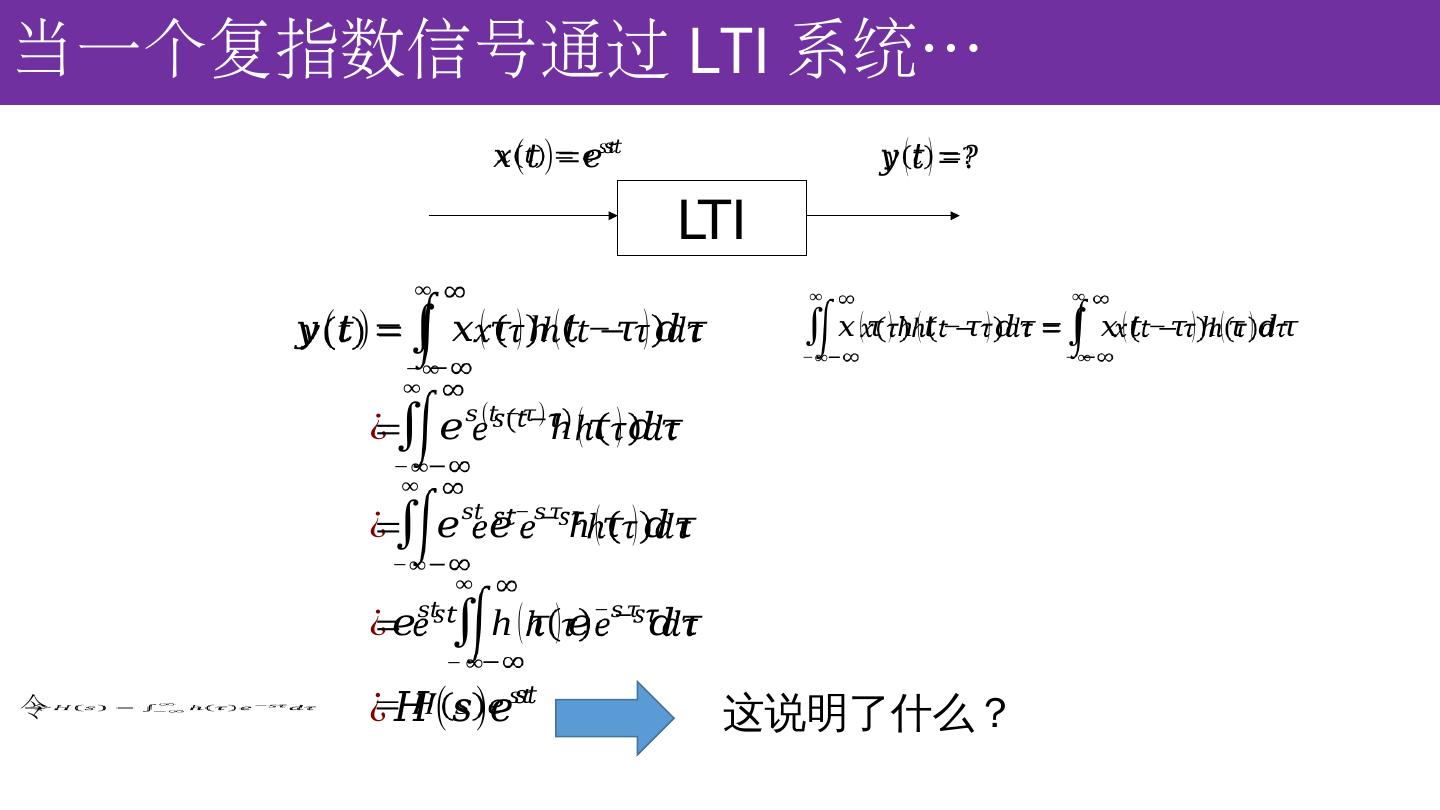
22 .当 一 个复指数信号通过 LTI 系统 … LTI 令 这说明了什么？
23 .说明了 LTI 系统对复指数信号的响应仍然是复指数信号。
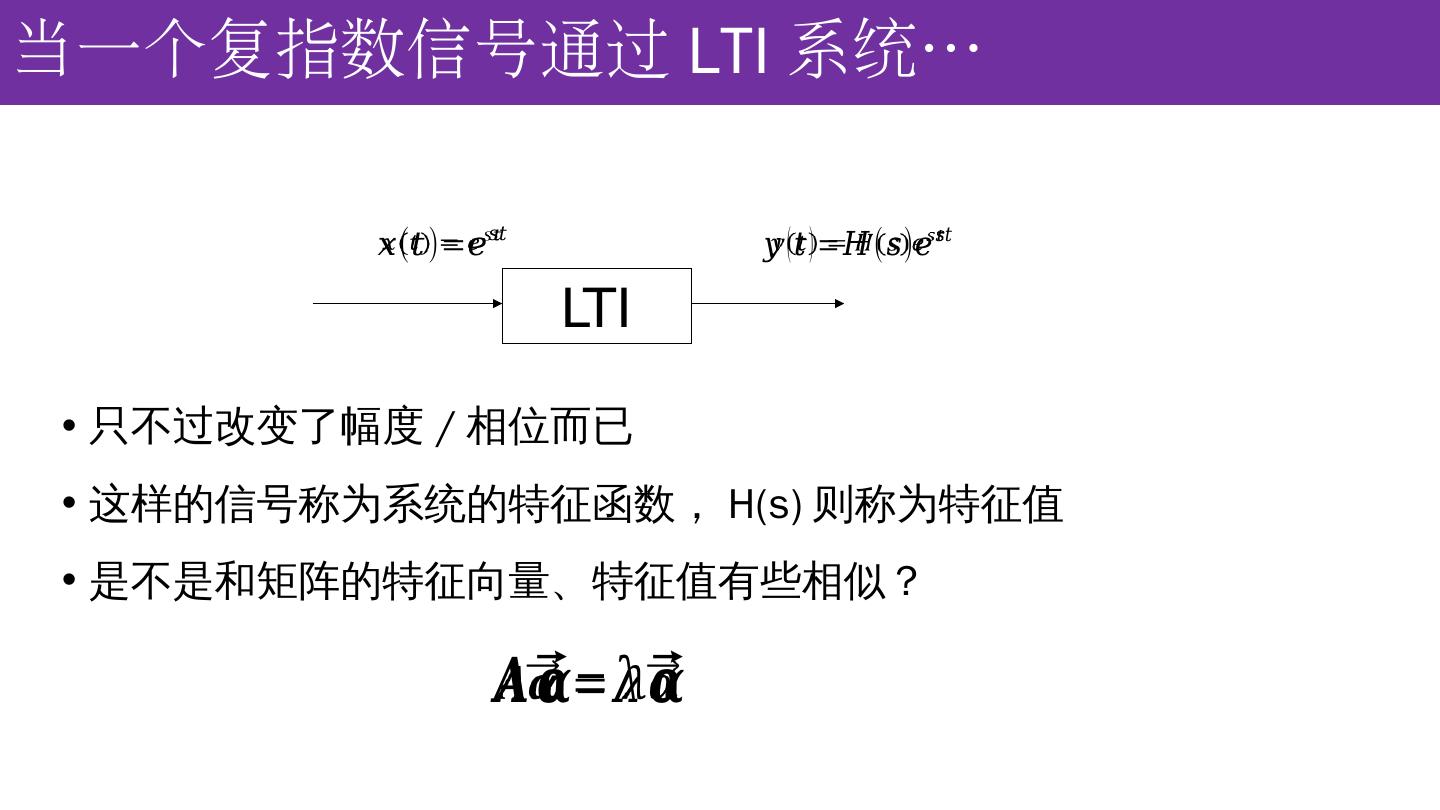
24 .当 一 个复指数信号通过 LTI 系统 … LTI 只不过改变了幅度 / 相位而已 这样的信号称为系统的特征函数， H(s) 则称为特征值 是不是和矩阵的特征向量、特征值有些相似？
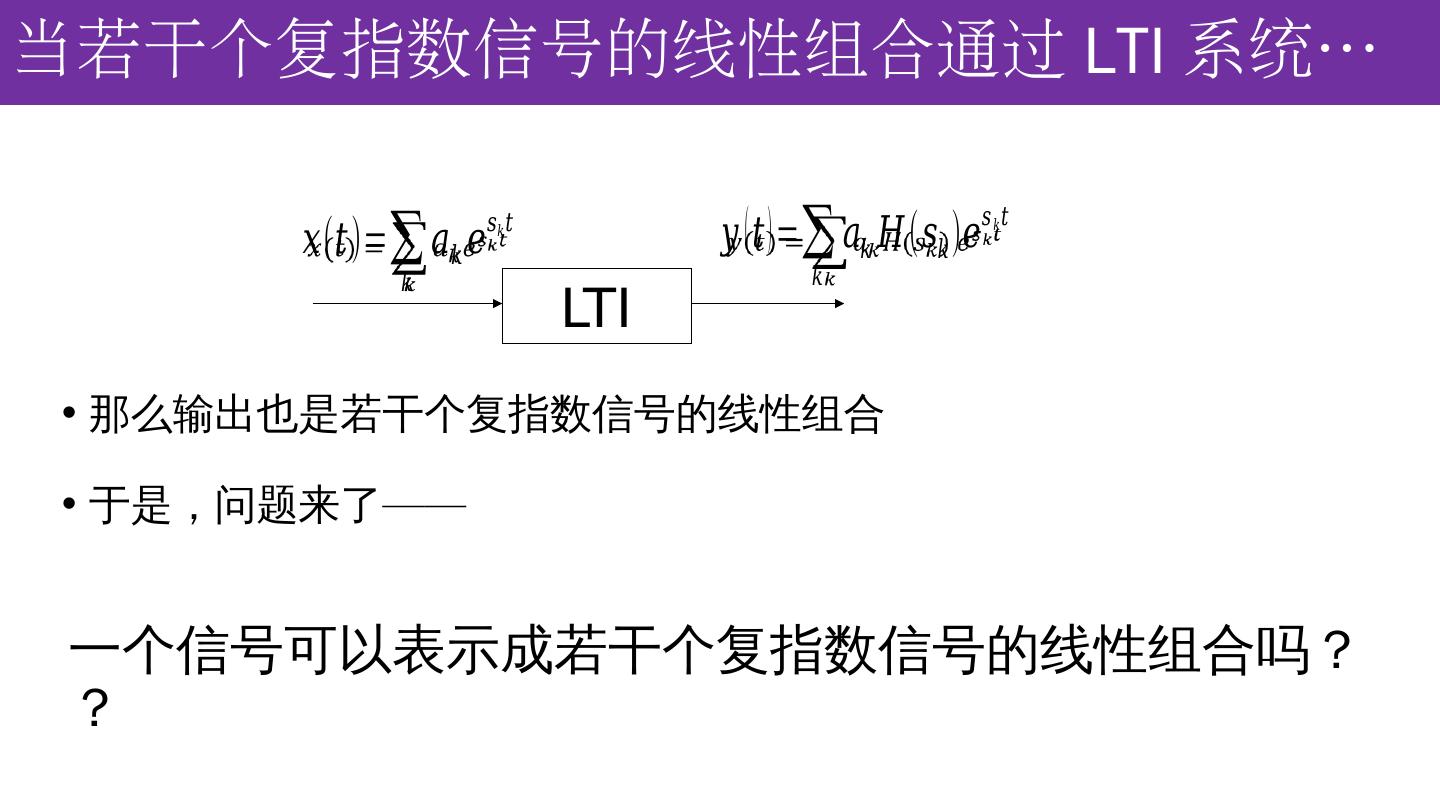
25 .当若干个复指数信号的线性组合通过 LTI 系统 … LTI 那么输出也是若干个复指数信号的线性组合 于是，问题来了 —— 一个信号可以表示成若干个复指数信号的线性组合吗？？
26 .类比 … 一 个向量如何表示为若干个向量的线性组合？ 想 办法搞到该向量所在空间的一组正交基 定义在 区间的两个函数 , ，满足 正交的完备性 什么是正交？ 三角函数集 复指数函数集 都定义在区间 简称：搞基。。 Walsh 函数集 …… 频率 序 率
27 .用正交基表示信号 选用三角函数集来表示信号 选用复指数函数集 三角函数集 复指数函数集 都定义在区间 这是什么？
28 .傅里叶级数 如何求系数？ 两边同乘以 两边同时在一个周期内积分 交换等式右边积分 与 求和符号 当 k=n 时，为 T ； 否则为 0 于是乎 结果 是
29 .用正交基表示信号 我们换一种表达方式 令 那么 于是 将 T 换掉
热门城市
