- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
快速傅里叶变换
展开查看详情
1 .快速傅里叶变换 Fast Fourier Transform
2 .应用 傅里叶变换计算 / 图像音频 多项式乘法 / 卷积 大数相乘 压缩
3 .多项式 一个以 x 为变量的多项式定义在一个代数域 F 上,将函数 表示为形式和: 其中 为多项式系数,若多项式 A 的最高次的非零系数为 ,则该多项式的 次数 为 k ,记 。 定义严格大于一个多项式次数的整数都是该多项式的 次数界
4 .多项式加法与乘法 多项式加法 若 , 次数 界均为 n ,则 多项式 乘法 注意 ,意味着如果 A 的 次数界为 , B 的次数界为 ,则 C 的次数界为 ,也可记为
5 .多项式的表示 系数表示 对于次数界为 n 的多项式 而言,其 系数表达 是一个由系数组成的向量 则多项式乘法 其中 复杂度 = 点 值表示 一 个次数 界 为 n 的多项式 的 点值表达 就是一个由 n 个点值对所组成的集合 其中 且 各不相同 则 复杂 度
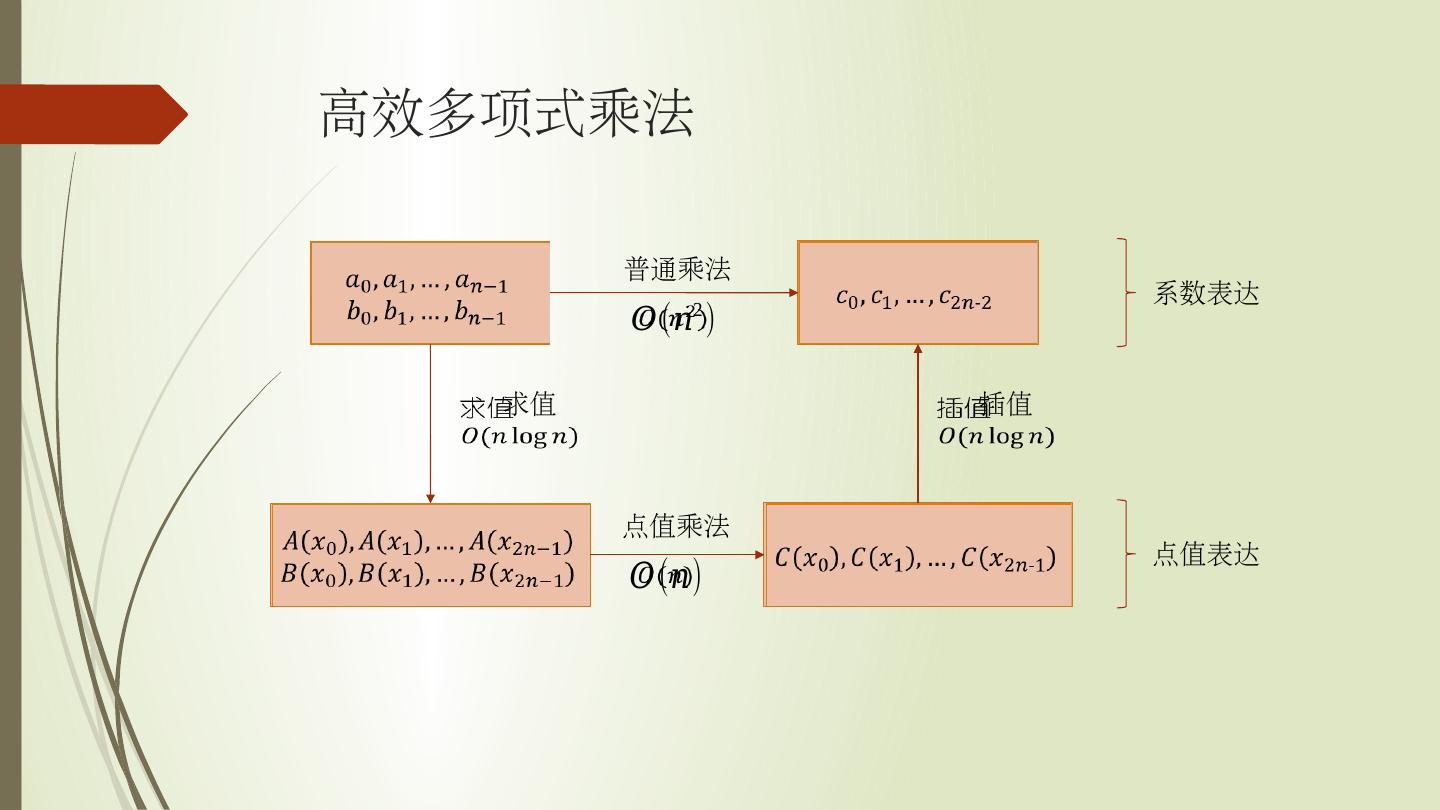
6 .高效多项式乘法 求值 普通乘法 点值乘法 插值 系数表达 点值 表达
7 .插值多项式的唯一性 求值计算的逆过程称为 插值 ,即从一个多项式的点值表达确定其系数表达形式 求值过程 等价于 由定理得,若 均不相同且个数等于 ,则该矩阵可逆 。 又因为可逆矩阵唯一,因此插值多项式唯一 通过精心地挑选求值点,比如单位复数根,则可以在 内对系数向量进行离散傅里叶变换 (DFT) ,得到相应的点值表达。也可以在 内 对点值对进行逆 DFT , 得到相应 的系数表达。
8 .复数及基本运算 形如 的数称为复数,其中 为虚数单位, 加法: 乘法 :
9 .欧拉公式 麦克劳林级数(即在 0 处的泰勒展开,该幂级数在整个复平面绝对收敛) 以 代替 展开式中的 ,得
10 .单位复数根 n 次单位复数根是满足 的复数 这样的复数恰好有 n 个: 因为 值 称为 主 n 次单位根 ,所有其他 n 次单位复数根都是 幂次 n 个 n 次单位复数根 乘法意义下形成一个群,该群与整数模 n 加法群 同构,即
11 .离散傅里叶变换 DFT 现在我们要计算次数界为 n 的 多项式 ,在 处的值,(注意此处的 n 已填充为原来的两倍长)。 假设 A 以系数形式给出, ,定义 向量 就是系数向量 的离散傅里叶变换。记为
12 .几个重要引理 消去引理 对任意整数 ,有 因为 ,得 推论 折半引理 如果 n>0 且为偶数,那么前 n/2 个 n 次单位复数根的平方等于后 n/2 个 n 次单位复数根的 平方 因为 ,所以 求和引理 对任意整数 和不能被 n 整除的非 零 整数 k ,有 根据等比数列求和公式
13 .快速傅里叶变换 FFT 假设 n 恰好是 2 的整数幂,不够的以 0 填充 FFT 利用分治策略,将 中奇偶下标的系数分离并重新定义两个新的次数为 n/2-1 的多项式 与 : 易得 根据折半引理, , ,因此 即将一个 n 个元素的 划分为两个规模为 n/2 的 时间复杂度
14 .递归版 FFT 伪代码
15 .逆 DFT 记 ,其中 的 的元素为 定理 : 的 的元素为 证:考虑 中 的 元素 根据求和引理,若 ,则和为 0 ,否则为 1 ,因此
16 .逆 DFT 因此 ,即 , , 中 的 元素 为 易 得 可以发现插值过程与求值过程的 FFT 形式类似,仅需要将求值中的主 n 次单位根 替换为 ,最后每个元素除以 n
17 .迭代 FFT 实现 0 2 4 6 8 10 12 14
18 .洛谷 luogu.org