- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Trie & Search树
展开查看详情
1 .Trie and Search Trees Dr. Andrew Wallace PhD BEng (hons) EurIng andrew.wallace@cs.umu.se
2 .Overview Trie Binary s earch trees
3 .Trie Special type of tree re trie val Dynamic sets Key is a string Root node is an empty string
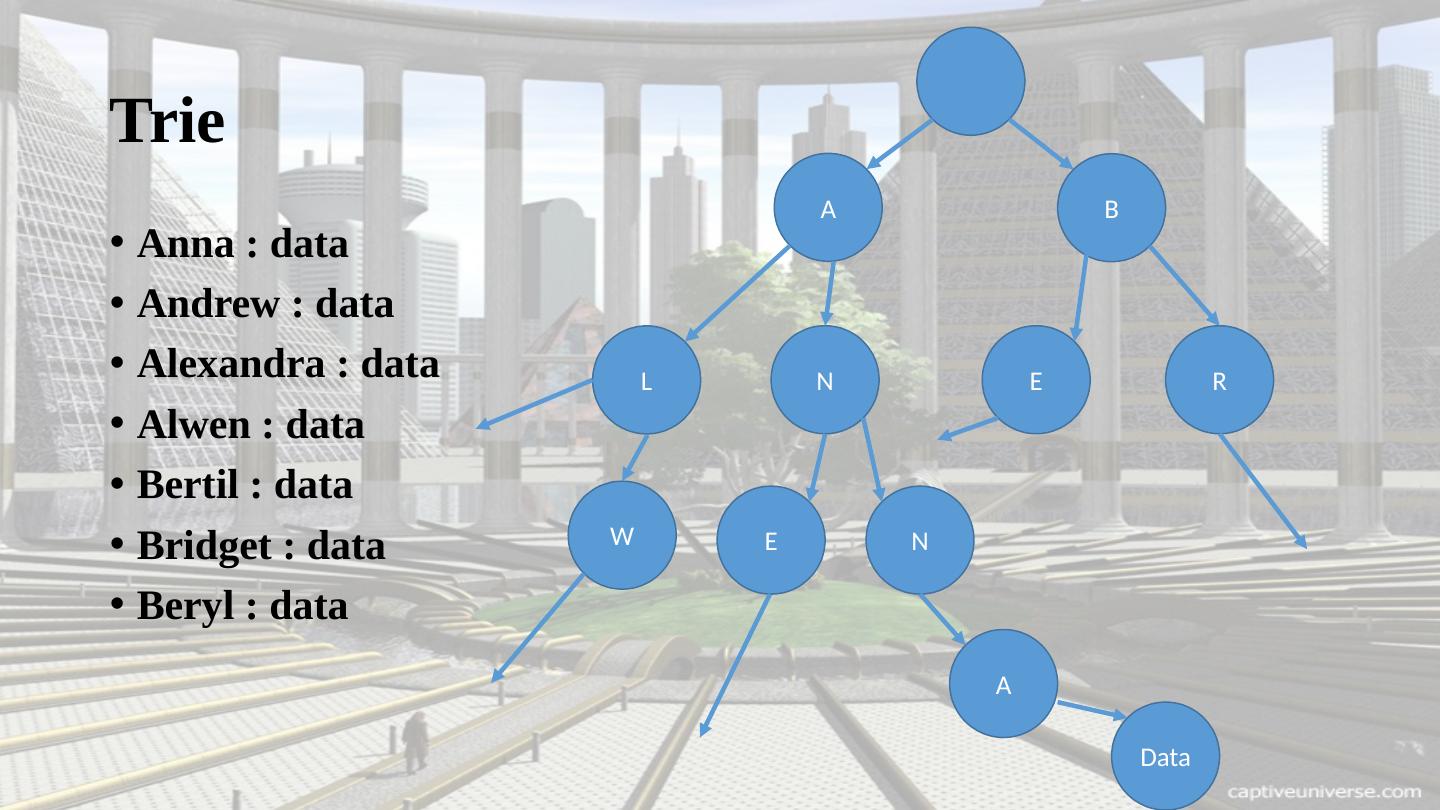
4 .Trie Anna : data Andrew : data Alexandra : data Alwen : data Bertil : data Bridget : data Beryl : data A B L N E R W E N A Data
5 .Trie Implementation As a table 2 x 2 array One columns per letter in the alphabet, n One row per node, m l og 2 m to represent the data
6 .Trie Implementation As a linked list Each node contains A letter Link to child de la Brandais tree
7 .Trie operations Insert child Delete child Child Look up
8 .Trie implementation Auto correct File structures DNA sequencing Data compression LZ78 Huffman encoding
9 .Trie implementation LZ78 Lossless data compression Dictionary based Random access
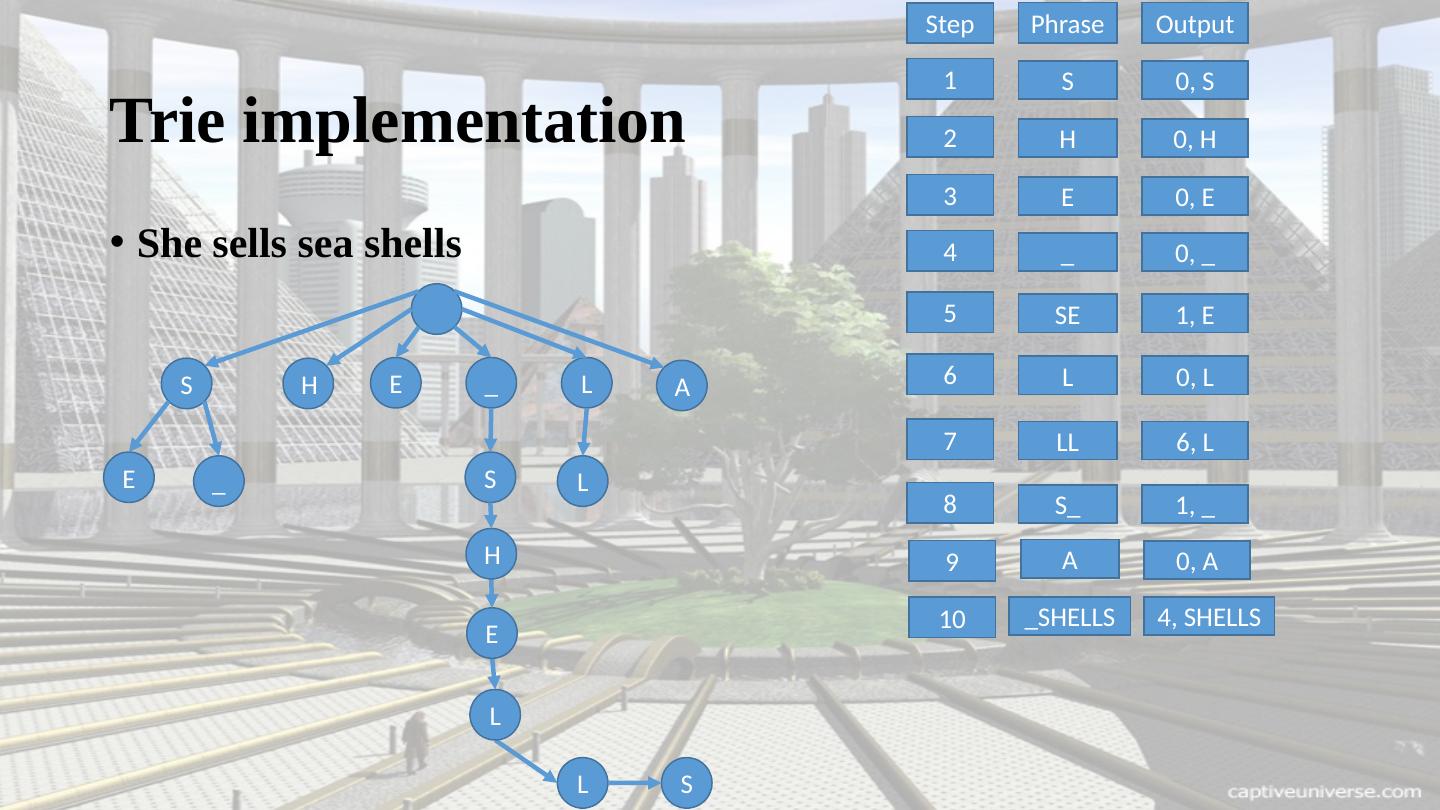
10 .Trie implementation She sells sea shells S H E _ L S _ E A Step Phrase Output 1 S 0, S 2 H 0, H 3 E 0, E 4 _ 0, _ 5 SE 1 , E 6 L 0, L 7 LL 6, L 8 S_ 1, _ 9 A 0, A 10 _SHELLS 4, SHELLS L S E L L H
11 .Trie Encode(n) Dictionary empty Prefix empty DictionaryIndex 1 while(n is not empty ) Char next character in n if(Prefix + Char exists in the Dictionary) Prefix Prefix + Char else if(Prefix is empty) CodeWordForPrefix 0 else CodeWordForPrefix DictionaryIndex for Prefix Output: ( CodeWordForPrefix , Char) insertInDictionary ( ( DictionaryIndex , Prefix + Char) ) DictionaryIndex ++ Prefix empty
12 .Huffman coding Frequency encoding Frequency Value 5 1 8 2 10 3 15 4 20 5 8:2 5:1 13:*
13 .Huffman coding Frequency Value 10 3 15 4 20 5 13 * 13:* 10:3 2 3:*
14 .Huffman coding Frequency Value 15 4 20 5 20:* 15:3 35:* 23 *
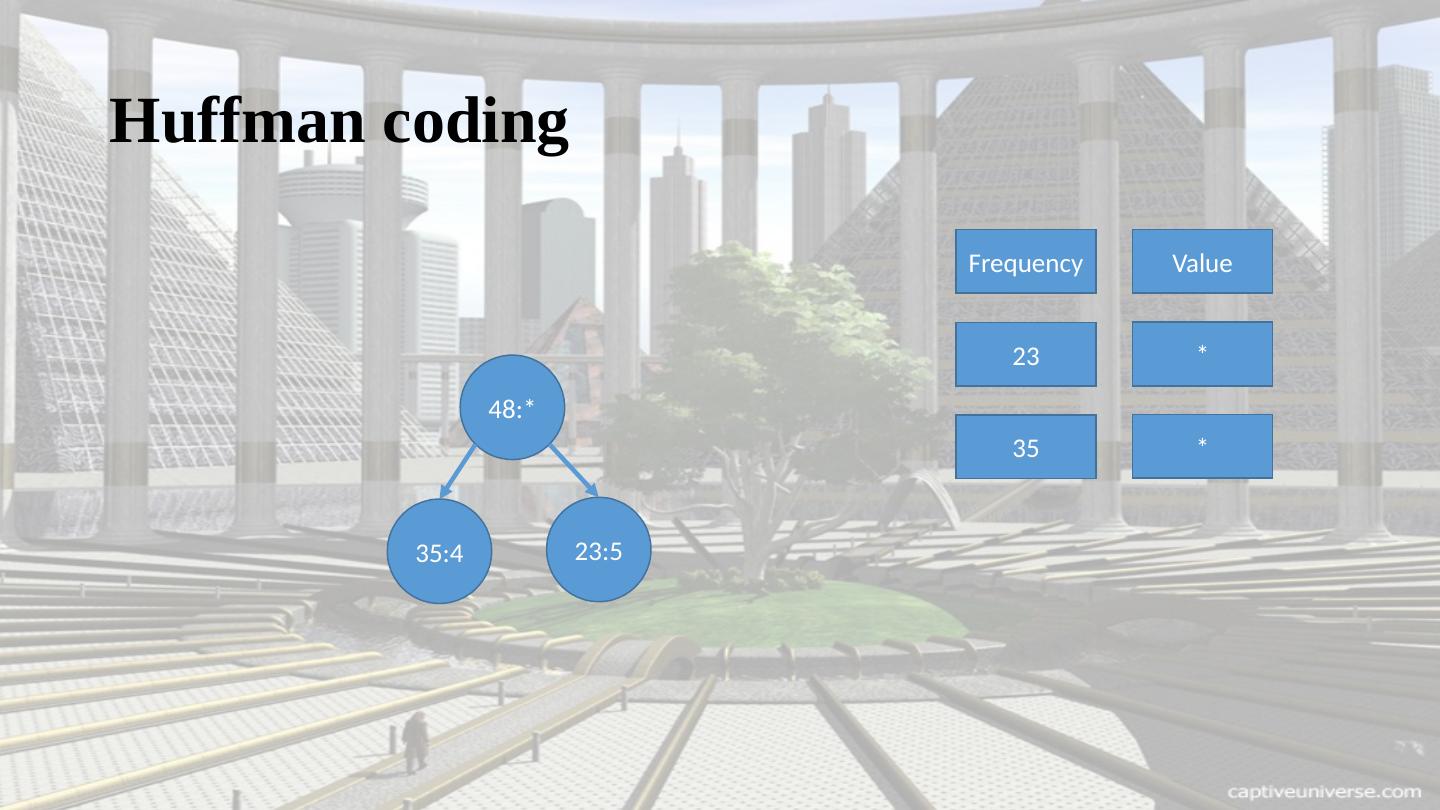
15 .Huffman coding Frequency Value 23 * 23:5 35:4 48:* 35 *
16 .Huffman coding Frequency Value 48 * 3 5:* 23:* 48:*
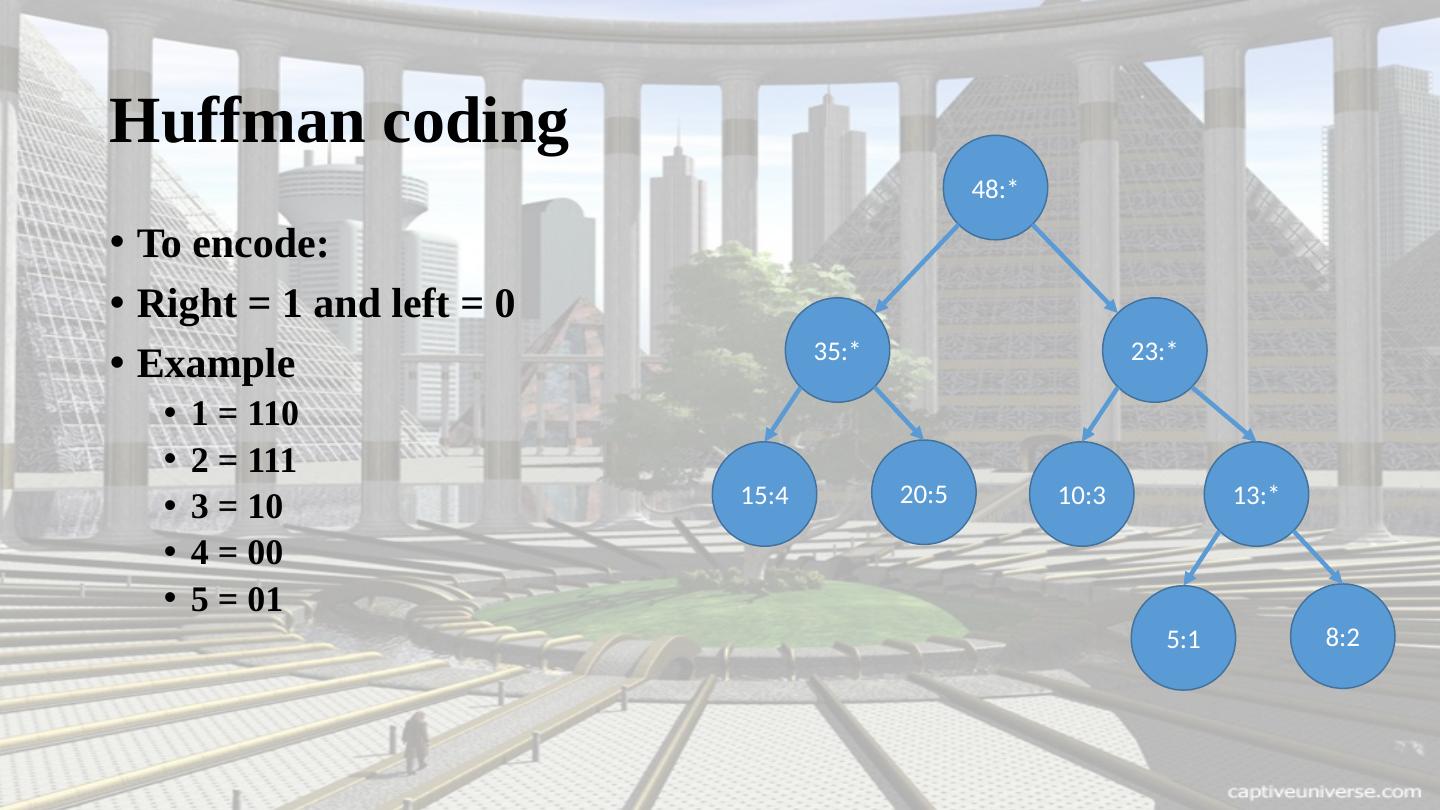
17 .Huffman coding To encode: Right = 1 and left = 0 Example 1 = 110 2 = 111 3 = 10 4 = 00 5 = 01 8:2 5:1 13:* 10:3 2 3:* 20:5 15:4 35:* 48:*
18 .Huffman coding Applications Zip file compression Jpeg PNG
19 .Binary Search trees Each node has max two child nodes Relationship between child nodes Nodes key is larger than all the nodes in the left sub tree Nodes key is smaller than all the nodes in the right sub tree 10 8 18 5 9 12 23
20 .Binary Search trees Binary search tree and a binary tree In a binary search tree all nodes much have a label Delete and Insert needs a label as does create tree for the root Delete can break the tree Fix it downwards Insert must insert in sorted order
21 .Binary Search trees Operations Search Insert Delete
22 .Binary Search trees Search Fast if tree is ordered Does node have value x? Where is 12? Search left if node value is greater than x Search right if node value is less than x How long will it take? Tree is complete O(log n ) 10 8 18 5 9 12 23
23 .Binary Search trees Searching a tree TreeSearch (x, k) if x = NULL or k = key[x] then return x if k key[x] then return TreeSearch (left[x], k) else return TreeSearch (right[x], k)
24 .Binary Search trees Insert Keep the tree complete Check left sub tree. If it is full, insert the value in the higher tree and move old down the tree 10 6 18 5 8 9 9 10 10
25 .Binary Search trees TreeInsert( T,z ) y NULL x NULL while x = NULL do y x if key[z] < key[x] then x left[x] else x right[x] p[z] y if y = NULL then root[T] = z else if key[z] < key[y] then left[y] z else right[y] z
26 .Binary Search trees Delete a node Case 1 No sub trees Case 2 One sub tree Case 3 Two sub trees 10 8 18 5 9 12
27 .Binary Search trees Case 2 Move sub tree to the delete node’s position Delete 18 Move 12 upwards 10 8 18 5 9 12 12
28 .Binary Search trees Case 3 Delete the node Promote the lowest value in the right sub tree Delete 10 Promote 12 10 8 18 5 9 12 12
29 .Binary Search trees TreeDelete (T, z) i f left[z] = NULL or right[z] = NULL then y TreeSuccessor (z) if left[y] = NULL then x left[y] else x right[y] if x = NULL then p[x] p[y] if p[y] = NULL then root[T] x else if y = left[p[y]] then left[p[y]] x else right [p[y]] x if y = z then key[z] key[y] return y