Lecture 9 预取

1 .CSC D70: Compiler Optimization Prefetching Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Phillip Gibbons

2 .The Memory Latency Problem  processor speed >>  memory speed caches are not a panacea 2

3 .Prefetching for Arrays: Overview Tolerating Memory Latency Prefetching Compiler Algorithm and Results Implications of These Results 3

4 .Coping with Memory Latency Reduce Latency: Locality Optimizations reorder iterations to improve cache reuse Tolerate Latency: Prefetching move data close to the processor before it is needed 4

5 .Tolerating Latency Through Prefetching overlap memory accesses with computation and other accesses 5 Without Prefetching With Prefetching Time Load A Load B Fetch A Fetch B Load A Load B Prefetch A Prefetch B Fetch A Fetch B Executing Instructions Stalled Waiting for Data

6 .Types of Prefetching Cache Blocks: (-) limited to unit-stride accesses Nonblocking Loads: (-) limited ability to move back before use Hardware-Controlled Prefetching : (-) limited to constant-strides and by branch prediction (+) no instruction overhead Software-Controlled Prefetching : (-) software sophistication and overhead (+) minimal hardware support and broader coverage 6

7 .Prefetching Goals Domain of Applicability Performance Improvement maximize benefit minimize overhead 7

8 .Prefetching Concepts possible only if addresses can be determined ahead of time coverage factor = fraction of misses that are prefetched unnecessary if data is already in the cache effective if data is in the cache when later referenced Analysis :  what to prefetch maximize coverage factor minimize unnecessary prefetches Scheduling :  when/how to schedule prefetches maximize effectiveness minimize overhead per prefetch 8

9 .Reducing Prefetching Overhead instructions to issue prefetches extra demands on memory system important to minimize unnecessary prefetches 9 Hit Rates for Array Accesses

10 .Compiler Algorithm Analysis : what to prefetch Locality Analysis Scheduling : when/how to issue prefetches Loop Splitting Software Pipelining 10

11 .Steps in Locality Analysis 1. Find data reuse if caches were infinitely large, we would be finished 2. Determine “localized iteration space” set of inner loops where the data accessed by an iteration is expected to fit within the cache 3. Find data locality: reuse  localized iteration space  locality 11

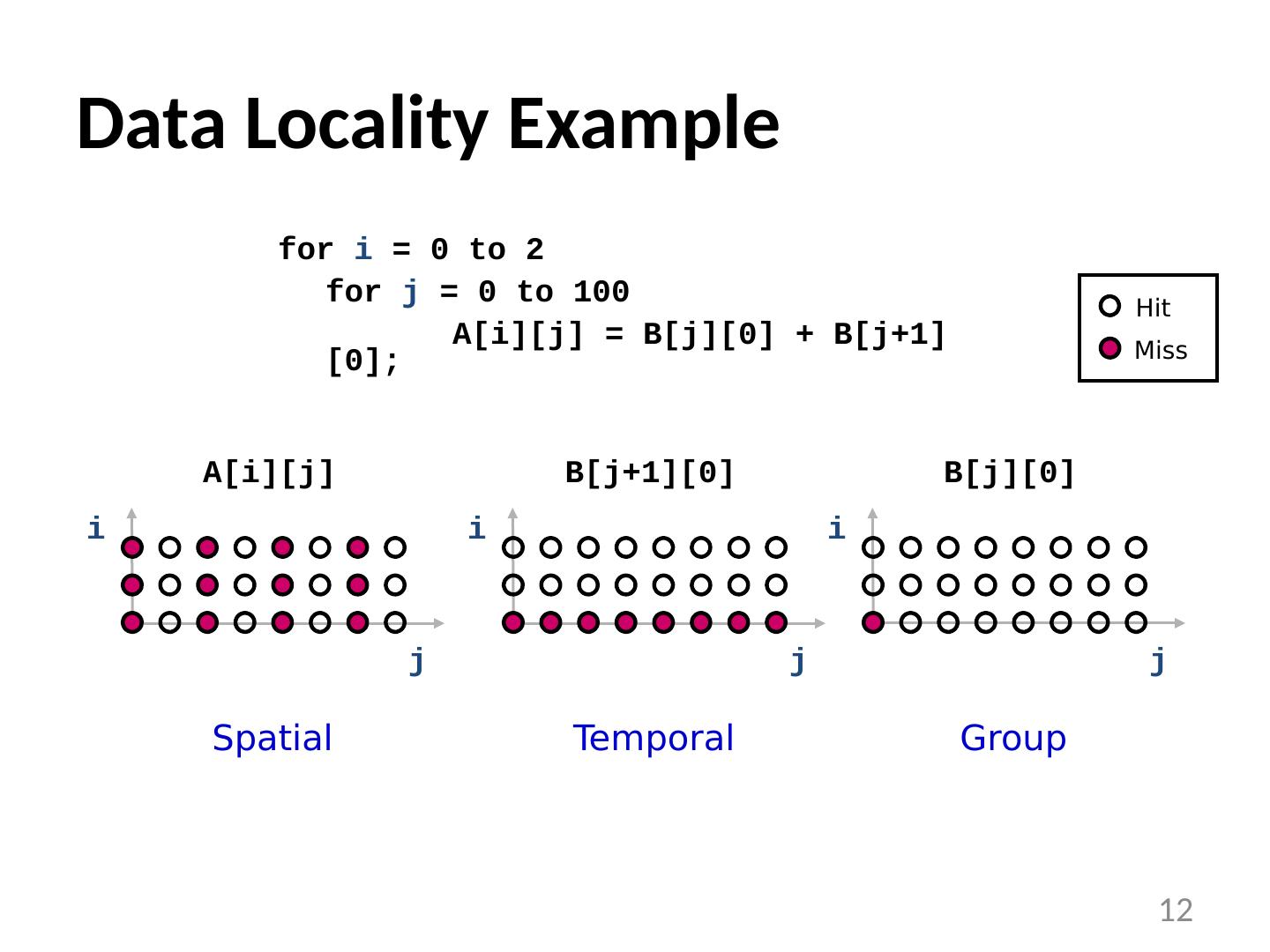
12 .Data Locality Example 12 for i = 0 to 2 for j = 0 to 100 A[ i ][j] = B[j][0] + B[j+1][0]; Hit Miss i j A[i][j] Spatial i j B[j+1][0] Temporal i j B[j][0] Group

13 .Reuse Analysis: Representation Map n loop indices into d array indices via array indexing function: for i = 0 to 2 for j = 0 to 100 A[ i ][j] = B[j][0] + B[j+1][0]; 13

14 .Temporal reuse occurs between iterations and whenever: Rather than worrying about individual values of and, we say that reuse occurs along direction vector when: Solution : compute the nullspace of H Finding Temporal Reuse 14

15 .Temporal Reuse Example Reuse between iterations (i 1 ,j 1 ) and (i 2 ,j 2 ) whenever: True whenever j 1 = j 2 , and regardless of the difference between i 1 and i 2 . i.e. whenever the difference lies along the nullspace of , which is span{(1,0)} (i.e. the outer loop). for i = 0 to 2 for j = 0 to 100 A[ i ][j] = B[j][0] + B[j+1][0]; 15

16 .Prefetch Predicate Example: 16 Locality Type Miss Instance Predicate None Every Iteration True Temporal First Iteration i = 0 Spatial Every l iterations (l = cache line size) ( i mod l) = 0 for i = 0 to 2 for j = 0 to 100 A[ i ][j] = B[j][0] + B[j+1][0]; Reference Locality Predicate A[ i ][j] ( j mod 2) = 0 B[j+1][0] i = 0 [ i j ] none spatial [ ] = [ i j ] temporal none [ ] =

17 .Compiler Algorithm Analysis : what to prefetch Locality Analysis Scheduling : when/how to issue prefetches Loop Splitting Software Pipelining 17

18 .Loop Splitting Decompose loops to isolate cache miss instances cheaper than inserting IF statements Apply transformations recursively for nested loops Suppress transformations when loops become too large avoid code explosion 18 Locality Type Predicate Loop Transformation None True None Temporal i = 0 Peel loop i Spatial ( i mod l) = 0 Unroll loop i by l

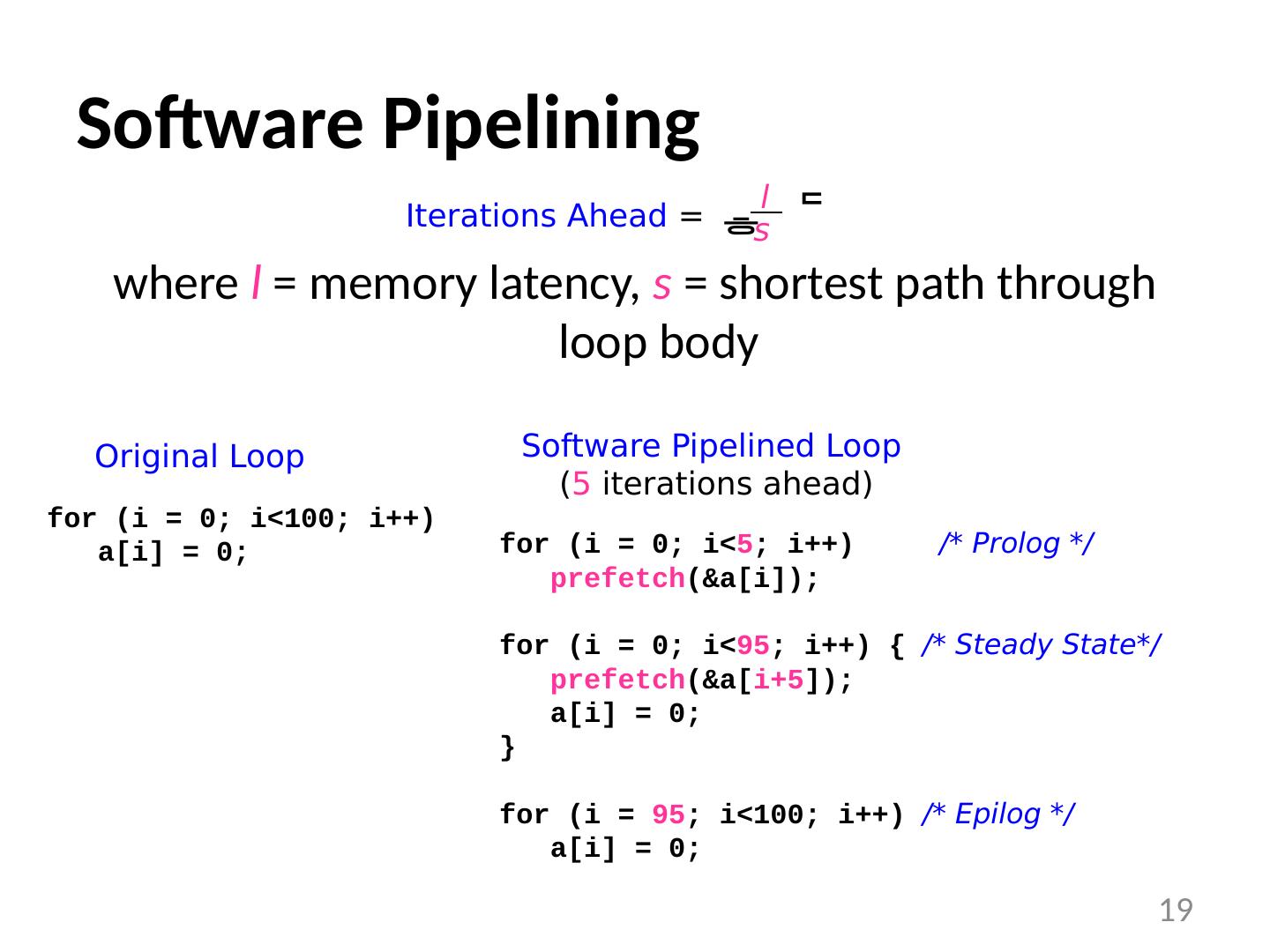
19 .Software Pipelining where l = memory latency, s = shortest path through loop body 19 Iterations Ahead =   l s for ( i = 0; i <100; i ++) a[ i ] = 0; Original Loop for ( i = 0; i < 5 ; i ++) /* Prolog */ prefetch (&a[ i ]); for ( i = 0; i < 95 ; i ++) { /* Steady State*/ prefetch (&a[ i+5 ]); a[ i ] = 0; } for ( i = 95 ; i <100; i ++) /* Epilog */ a[ i ] = 0; Software Pipelined Loop ( 5 iterations ahead)

20 .Example Revisited 20 for ( i = 0; i < 3; i ++) f or (j = 0; j < 100; j++) A[ i ][j] = B[j][0] + B[j+1][0]; Original Code prefetch (&A[0][0]); for (j = 0; j < 6; j += 2) { prefetch (&B[j+1][0]); prefetch (&B[j+2][0]); prefetch (&A[0][j+1]); } for (j = 0; j < 94; j += 2) { prefetch (&B[j+7][0]); prefetch (&B[j+8][0]); prefetch (&A[0][j+7]); A[0][j] = B[j][0]+B[j+1][0]; A[0][j+1] = B[j+1][0]+B[j+2][0]; } for (j = 94; j < 100; j += 2) { A[0][j] = B[j][0]+B[j+1][0]; A[0][j+1] = B[j+1][0]+B[j+2][0]; } for ( i = 1; i < 3; i ++) { prefetch (&A[ i ][0]); for (j = 0; j < 6; j += 2) prefetch (&A[ i ][j+1]); for (j = 0; j < 94; j += 2) { prefetch (&A[ i ][j+7]); A[ i ][j] = B[j][0] + B[j+1][0]; A[ i ][j+1] = B[j+1][0] + B[j+2][0]; } for (j = 94; j < 100; j += 2) { A[ i ][j] = B[j][0] + B[j+1][0]; A[ i ][j+1] = B[j+1][0] + B[j+2][0]; } } Code with Prefetching i j A[ i ][j] i j B[j+1][0] Cache Hit Cache Miss i = 0 i > 0

21 .Prefetching Indirections Analysis : what to prefetch both dense and indirect references difficult to predict whether indirections hit or miss Scheduling : when/how to issue prefetches modification of software pipelining algorithm 21 for ( i = 0; i <100; i ++) sum += A[index[ i ]];

22 .Software Pipelining for Indirections 22 for ( i = 0; i <100; i ++) sum += A[index[ i ]]; Original Loop for ( i = 0; i < 5 ; i ++) /* Prolog 1 */ prefetch (&index[ i ]); for ( i = 0; i < 5 ; i ++) { /* Prolog 2 */ prefetch (&index[ i+5 ]); prefetch (&A[index[ i ]]); } for ( i = 0; i < 90 ; i ++) { /* Steady State*/ prefetch (&index[ i+10 ]); prefetch (&A[index[ i+5 ]]); sum += A[index[ i ]]; } for ( i = 90; i <95; i ++) { /* Epilog 1 */ prefetch (&A[index[ i+5 ]]); sum += A[index[ i ]]; } for ( i = 95 ; i <100; i ++) /* Epilog 2 */ sum += A[index[ i ]]; Software Pipelined Loop ( 5 iterations ahead)

23 .Summary of Results Dense Matrix Code : eliminated 50% to 90% of memory stall time overheads remain low due to prefetching selectively significant improvements in overall performance (6 over 45%) Indirections, Sparse Matrix Code : expanded coverage to handle some important cases 23

24 .Prefetching for Arrays: Concluding Remarks Demonstrated that software prefetching is effective selective prefetching to eliminate overhead dense matrices and indirections / sparse matrices uniprocessors and multiprocessors Hardware should focus on providing sufficient memory bandwidth 24

25 .Prefetching for Recursive Data Structures 25

26 .Recursive Data Structures Examples: linked lists, trees, graphs, ... A common method of building large data structures especially in non-numeric programs Cache miss behavior is a concern because: large data set with respect to the cache size temporal locality may be poor little spatial locality among consecutively-accessed nodes Goal : Automatic Compiler-Based Prefetching for Recursive Data Structures 26

27 .Overview Challenges in Prefetching Recursive Data Structures Three Prefetching Algorithms Experimental Results Conclusions 27

28 .Scheduling Prefetches for Recursive Data Structures 28 Our Goal : fully hide latency thus achieving fastest possible computation rate of 1/W e.g., if L = 3W , we must prefetch 3 nodes ahead to achieve this

29 .Performance without Prefetching 29 computation rate = 1 / (L+W)