Lecture 8 内存优化

1 .CSC D70: Compiler Optimization Memory Optimizations Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry, Greg Steffan , and Phillip Gibbons

2 .Announcements Assignment 3 due on April 5th (Thursday) midnight Final Exam: Wednesday, April 11th, 19:00~20:30 , at IC120 2

3 .Pointer Analysis (Summary) Pointers are hard to understand at compile time! accurate analyses are large and complex Many different options : Representation, heap modeling, aggregate modeling, flow sensitivity, context sensitivity Many algorithms : Address-taken, Steensgarde , Andersen BDD-based, probabilistic Many trade-offs: space, time, accuracy, safety Choose the right type of analysis given how the information will be used 3

4 .Caches: A Quick Review How do they work? Why do we care about them? What are typical configurations today? What are some important cache parameters that will affect performance? 4

5 .Memory (Programmer’s View) 5

6 .Memory in a Modern System 6 CORE 1 L2 CACHE 0 SHARED L3 CACHE DRAM INTERFACE CORE 0 CORE 2 CORE 3 L2 CACHE 1 L2 CACHE 2 L2 CACHE 3 DRAM BANKS DRAM MEMORY CONTROLLER

7 .Ideal Memory Zero access time (latency) Infinite capacity Zero cost Infinite bandwidth (to support multiple accesses in parallel) 7

8 .The Problem Ideal memory’s requirements oppose each other Bigger is slower Bigger  Takes longer to determine the location Faster is more expensive Memory technology: SRAM vs. DRAM vs. Flash vs. Disk vs. Tape Higher bandwidth is more expensive Need more banks, more ports, higher frequency, or faster technology 8

9 .Memory Technology: DRAM Dynamic random access memory Capacitor charge state indicates stored value Whether the capacitor is charged or discharged indicates storage of 1 or 0 1 capacitor 1 access transistor Capacitor leaks through the RC path DRAM cell loses charge over time DRAM cell needs to be refreshed 9 row enable _bitline

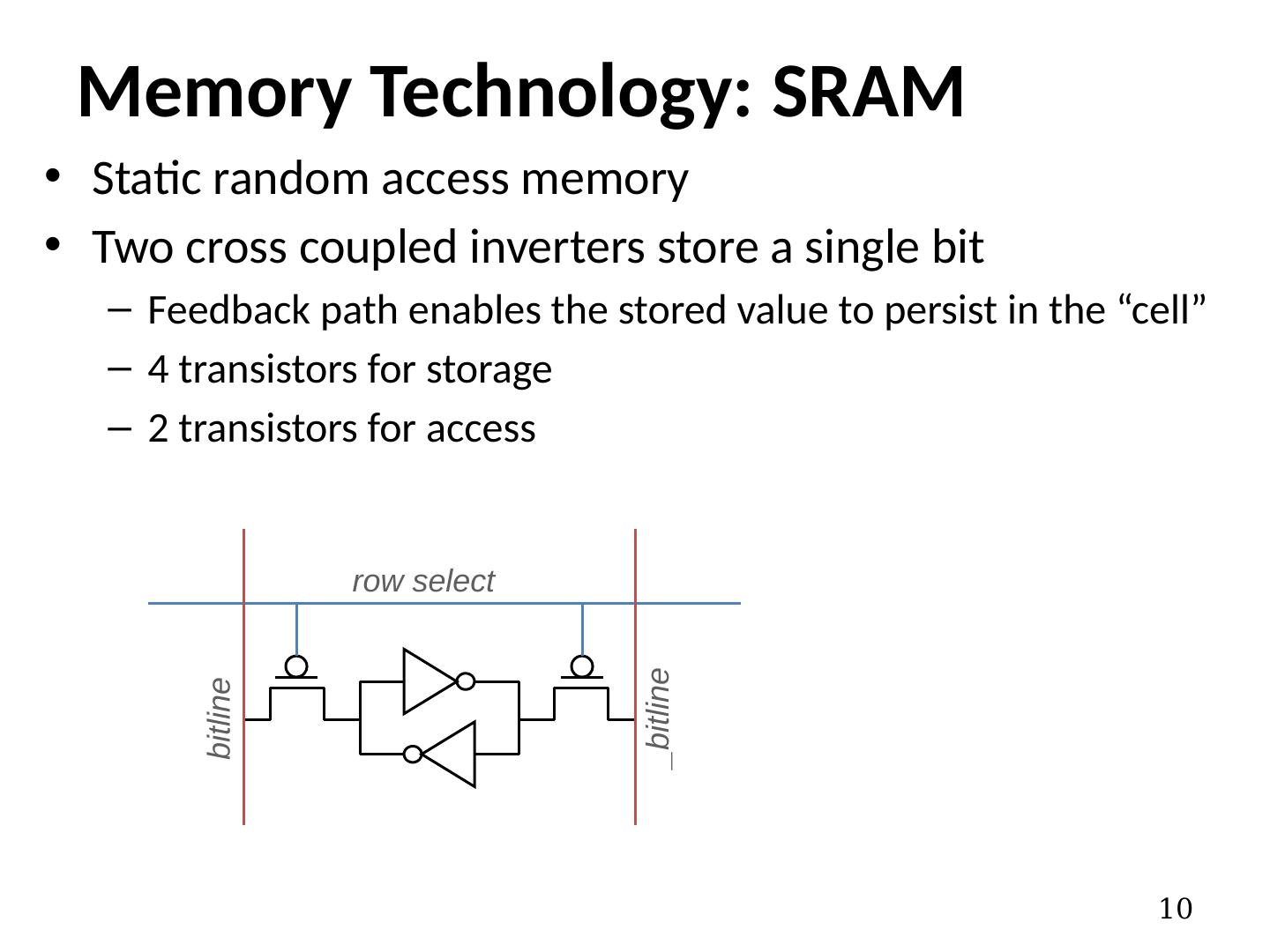
10 .Static random access memory Two cross coupled inverters store a single bit Feedback path enables the stored value to persist in the “cell” 4 transistors for storage 2 transistors for access Memory Technology: SRAM 10 row select bitline _bitline

11 .Why Memory Hierarchy? We want both fast and large But we cannot achieve both with a single level of memory Idea: Have multiple levels of storage (progressively bigger and slower as the levels are farther from the processor) and ensure most of the data the processor needs is kept in the fast( er ) level(s) 11

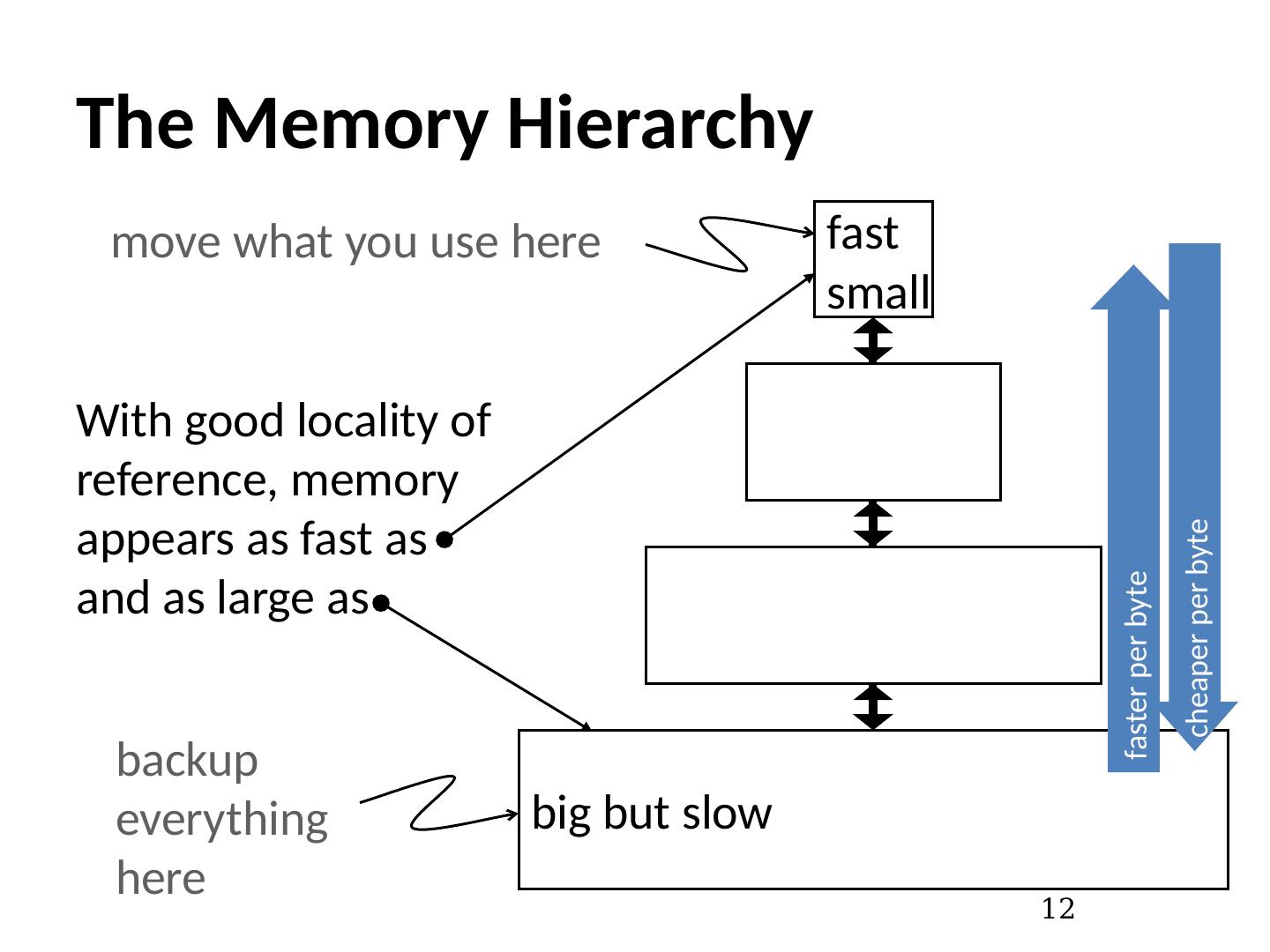
12 .The Memory Hierarchy 12 fast small big but slow move what you use here backup everything here With good locality of reference, memory appears as fast as and as large as faster per byte cheaper per byte

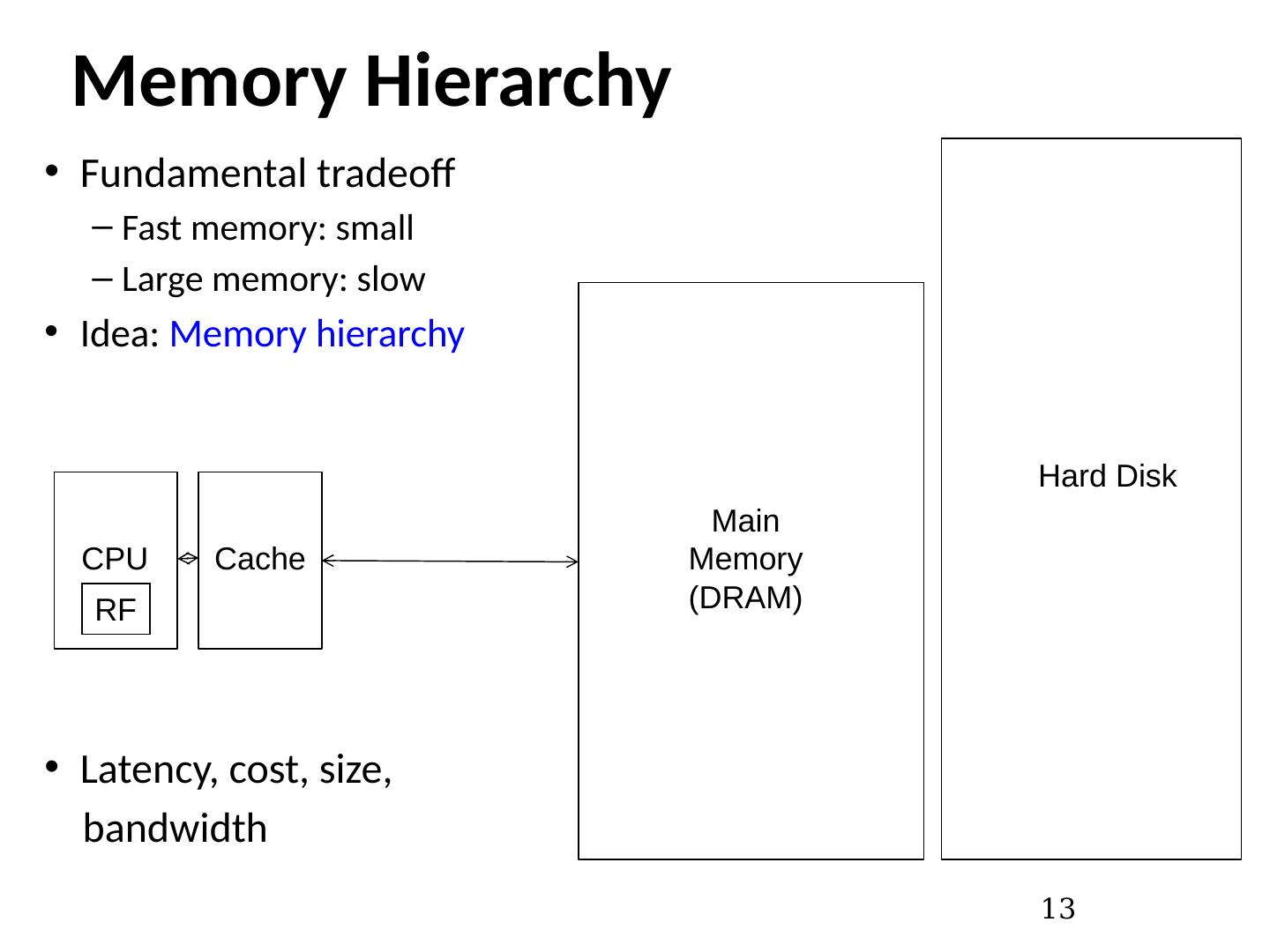
13 .Memory Hierarchy Fundamental tradeoff Fast memory: small Large memory: slow Idea: Memory hierarchy Latency, cost, size, bandwidth 13 CPU Main Memory (DRAM) RF Cache Hard Disk

14 .Caching Basics: Exploit Temporal Locality Idea: Store recently accessed data in automatically managed fast memory (called cache) Anticipation: the data will be accessed again soon Temporal locality principle Recently accessed data will be again accessed in the near future This is what Maurice Wilkes had in mind: Wilkes, “ Slave Memories and Dynamic Storage Allocation , ” IEEE Trans. On Electronic Computers, 1965. “ The use is discussed of a fast core memory of, say 32000 words as a slave to a slower core memory of, say, one million words in such a way that in practical cases the effective access time is nearer that of the fast memory than that of the slow memory. ” 14

15 .Caching Basics: Exploit Spatial Locality Idea: Store addresses adjacent to the recently accessed one in automatically managed fast memory Logically divide memory into equal size blocks Fetch to cache the accessed block in its entirety Anticipation: nearby data will be accessed soon Spatial locality principle Nearby data in memory will be accessed in the near future E.g., sequential instruction access, array traversal This is what IBM 360/85 implemented 16 Kbyte cache with 64 byte blocks Liptay , “ Structural aspects of the System/360 Model 85 II: the cache , ” IBM Systems Journal, 1968. 15

16 .Optimizing Cache Performance Things to enhance: temporal locality spatial locality Things to minimize: conflicts (i.e. bad replacement decisions) What can the compiler do to help? 16

17 .Two Things We Can Manipulate Time: When is an object accessed? Space: Where does an object exist in the address space? How do we exploit these two levers? 17

18 .Time: Reordering Computation What makes it difficult to know when an object is accessed? How can we predict a better time to access it? What information is needed? How do we know that this would be safe ? 18

19 .Space: Changing Data Layout What do we know about an object’s location ? scalars, structures, pointer-based data structures, arrays, code, etc. How can we tell what a better layout would be? how many can we create? To what extent can we safely alter the layout? 19

20 .Types of Objects to Consider Scalars Structures & Pointers Arrays 20

21 .Scalars Locals Globals Procedure arguments Is cache performance a concern here? If so, what can be done? int x ; double y ; foo ( int a ){ int i ; … x = a * i ; … } 21

22 .Structures and Pointers What can we do here? within a node across nodes What limits the compiler’s ability to optimize here? struct { int count; double velocity; double inertia; struct node *neighbors[N]; } node; 22

23 .Arrays usually accessed within loops nests makes it easy to understand “time” what we know about array element addresses : start of array? relative position within array double A[N][N], B[N][N]; … for i = 0 to N-1 for j = 0 to N-1 A[ i ][j] = B[j][ i ]; 23

24 .Handy Representation: “Iteration Space” each position represents an iteration for i = 0 to N-1 for j = 0 to N-1 A[i][j] = B[j][i]; i j 24

25 .Visitation Order in Iteration Space Note: iteration space  data space for i = 0 to N-1 for j = 0 to N-1 A[ i ][j] = B[j][ i ]; i j 25

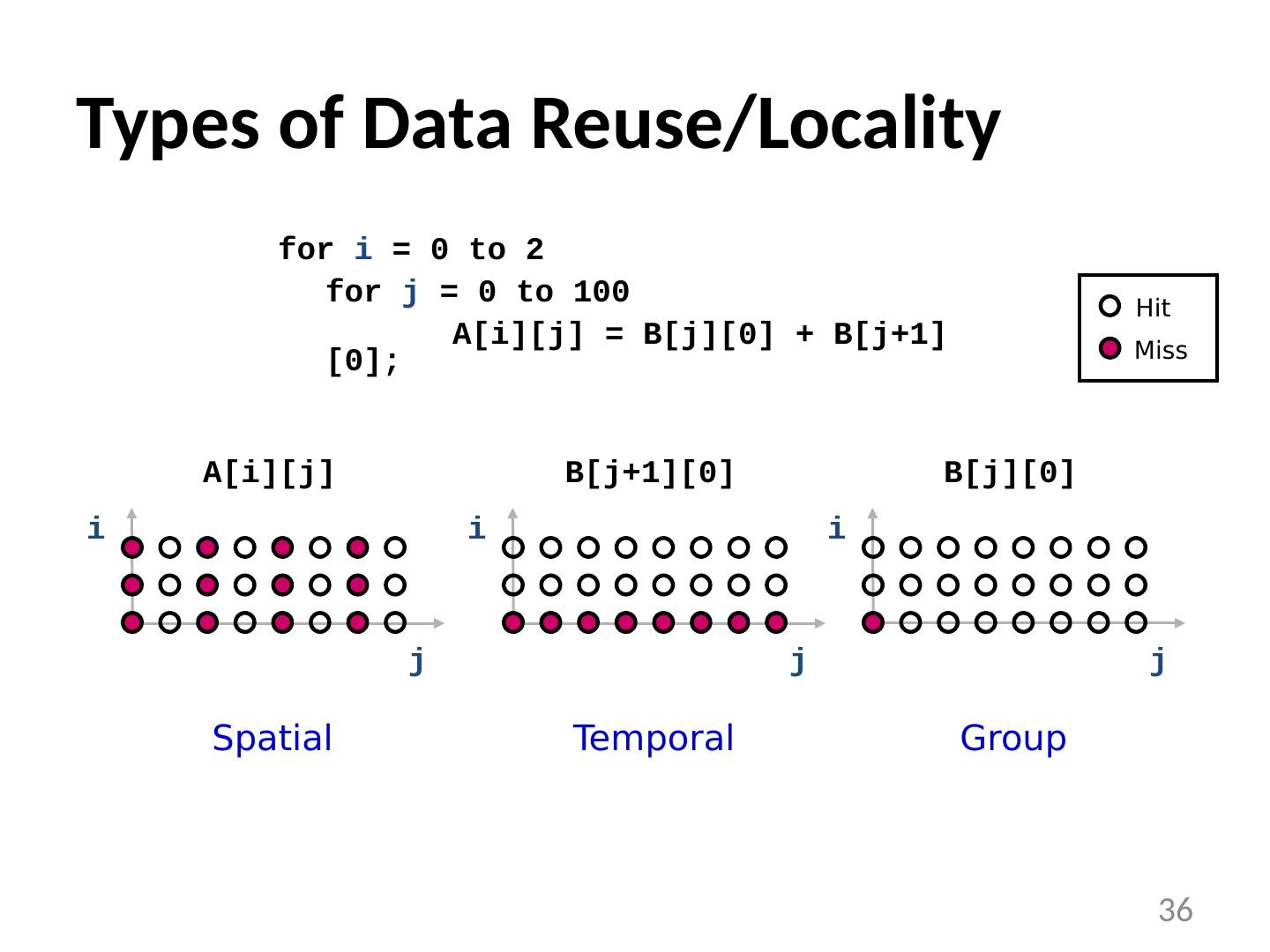
26 .When Do Cache Misses Occur? for i = 0 to N-1 for j = 0 to N-1 A[ i ][j] = B[j][ i ]; i j i j A B 26

27 .When Do Cache Misses Occur? for i = 0 to N-1 for j = 0 to N-1 A[i+j][0] = i*j; i j 27

28 .Optimizing the Cache Behavior of Array Accesses We need to answer the following questions: when do cache misses occur? use “ locality analysis ” can we change the order of the iterations (or possibly data layout) to produce better behavior? evaluate the cost of various alternatives does the new ordering/layout still produce correct results? use “ dependence analysis ” 28

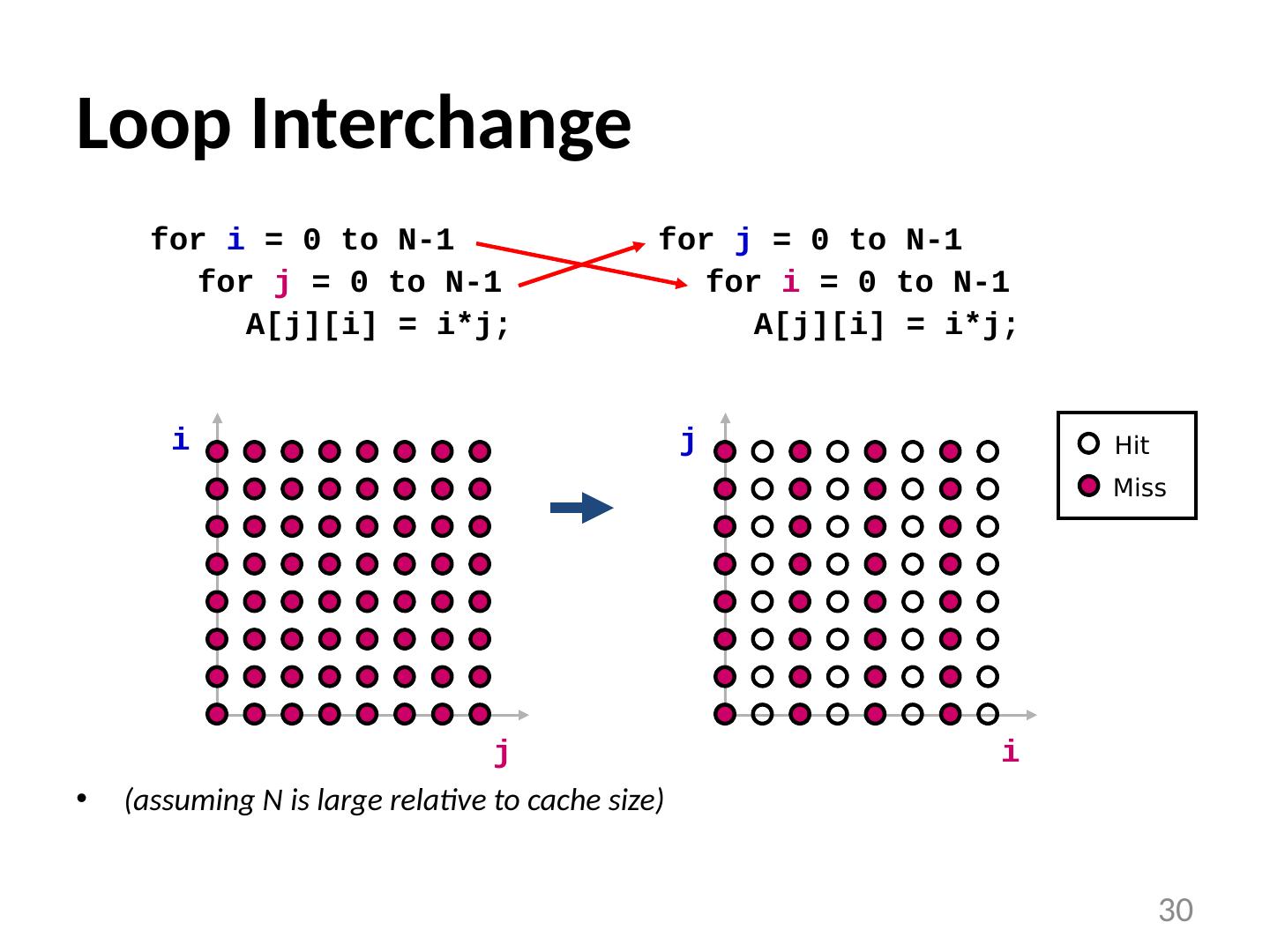
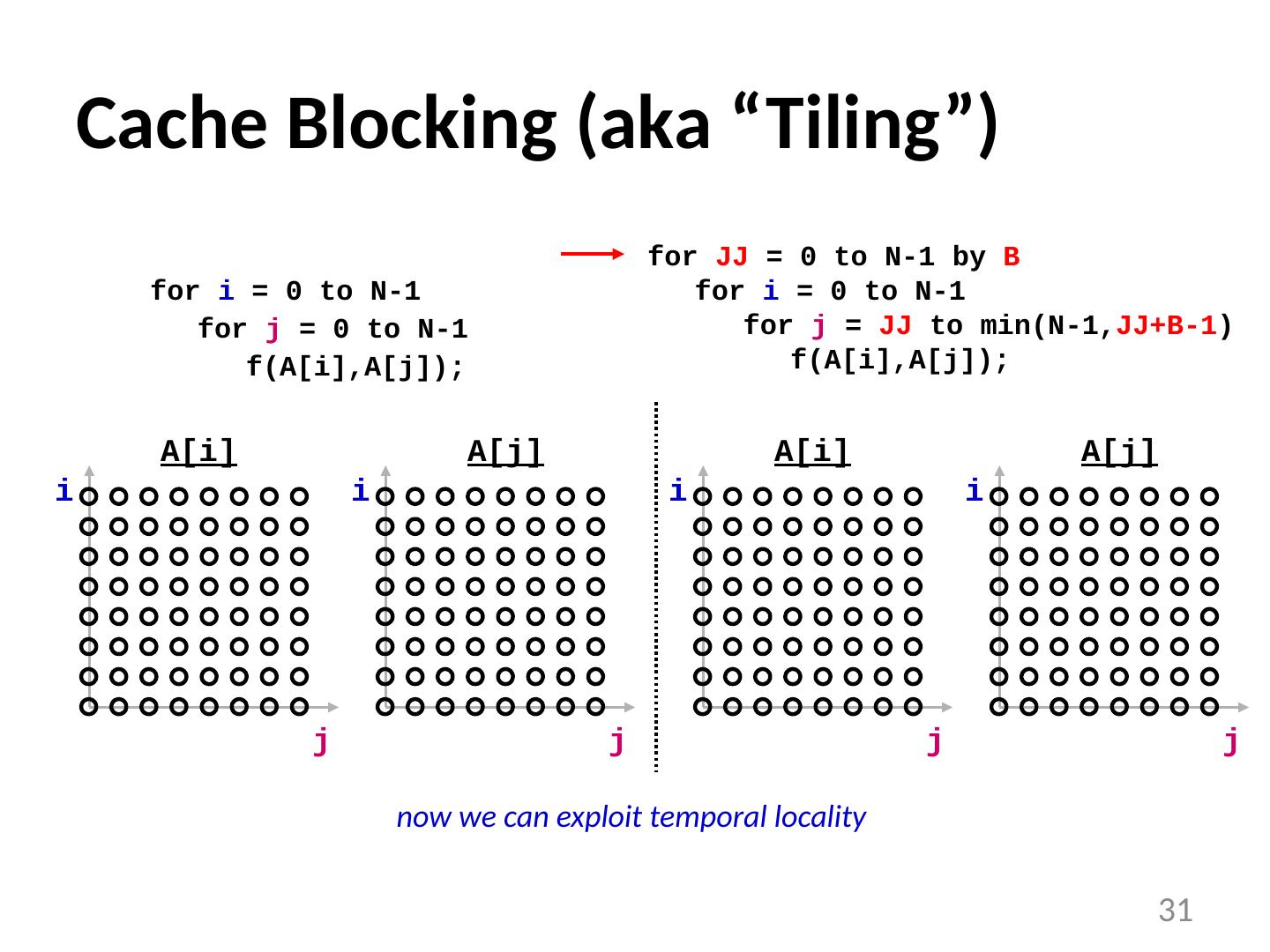
29 .Examples of Loop Transformations Loop Interchange Cache Blocking Skewing Loop Reversal … 29