Lecture 7 指针分析

1 .CSC D70: Compiler Optimization Pointer Analysis Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry, Greg Steffan , and Phillip Gibbons

2 .Basics Design Options Pointer Analysis Algorithms Pointer Analysis Using BDDs Probabilistic Pointer Analysis 2 Outline

3 .Pros and Cons of Pointers Many procedural languages have pointers e.g., C or C++: int *p = &x; Pointers are powerful and convenient can build arbitrary data structures Pointers can also hinder compiler optimization hard to know where pointers are pointing must be conservative in their presence Has inspired much research analyses to decide where pointers are pointing many options and trade-offs open problem: a scalable accurate analysis 3

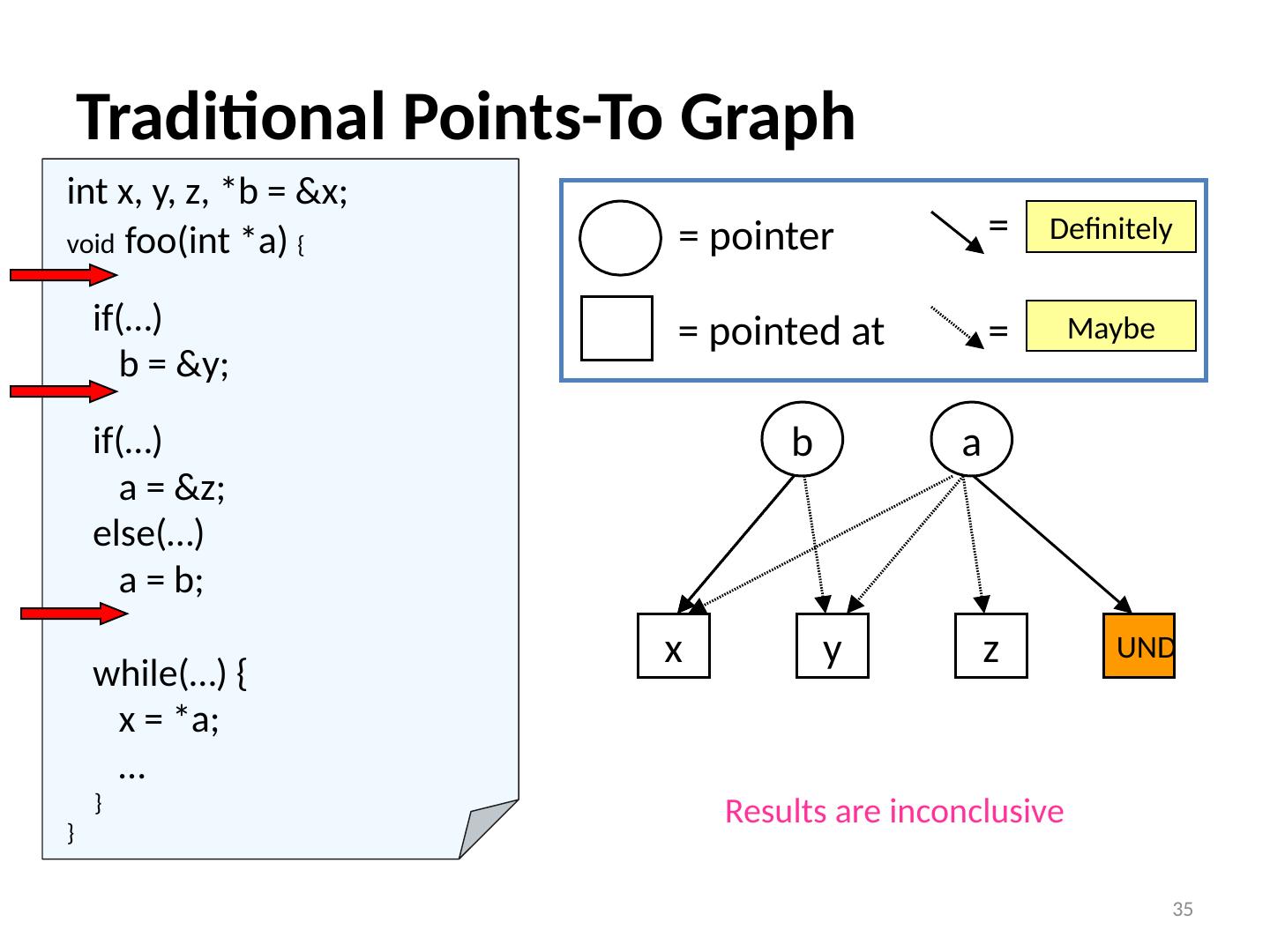
4 .Pointer Analysis Basics: Aliases Two variables are aliases if: they reference the same memory location More useful: prove variables reference different location 4 int x,y ; int *p = &x; int *q = &y; int *r = p; int **s = &q; Alias Sets ? {x, *p, *r} {y, *q, **s} {q, *s} p and q point to different locs

5 .The Pointer Alias Analysis Problem Decide for every pair of pointers at every program point : do they point to the same memory location? A difficult problem shown to be undecidable by Landi , 1992 Correctness : report all pairs of pointers which do/may alias Ambiguous : two pointers which may or may not alias Accuracy/Precision : how few pairs of pointers are reported while remaining correct i.e., reduce ambiguity to improve accuracy 5

6 .Many Uses of Pointer Analysis Basic compiler optimizations register allocation, CSE, dead code elimination, live variables, instruction scheduling, loop invariant code motion, redundant load/store elimination Parallelization instruction-level parallelism thread-level parallelism Behavioral synthesis automatically converting C-code into gates Error detection and program understanding memory leaks, wild pointers, security holes 6

7 .Challenges for Pointer Analysis Complexity : huge in space and time compare every pointer with every other pointer at every program point potentially considering all program paths to that point Scalability vs. accuracy trade-off different analyses motivated for different purposes many useful algorithms (adds to confusion) Coding corner cases pointer arithmetic (*p++), casting, function pointers, long-jumps Whole program? most algorithms require the entire program library code? optimizing at link-time only? 7

8 .Pointer Analysis: Design Options Representation Heap modeling Aggregate modeling Flow sensitivity Context sensitivity 8

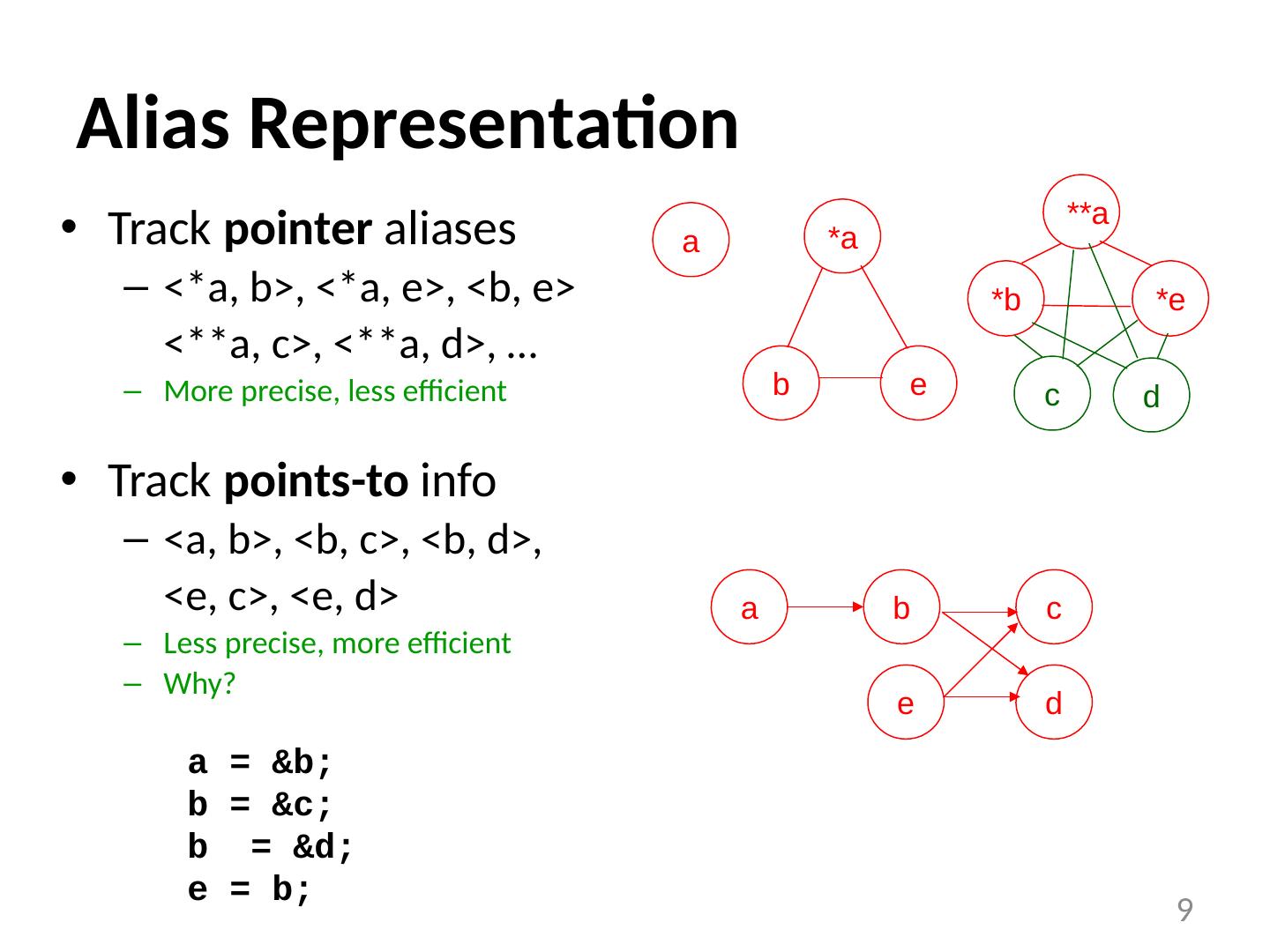
9 .Alias Representation 9 Track pointer aliases <*a, b>, <*a, e>, <b, e> <**a, c>, <**a, d>, … More precise, less efficient Track points-to info <a, b>, <b, c>, <b, d>, <e, c>, <e, d> Less precise, more efficient Why? a = &b; b = &c; b = &d; e = b; a b c d e a b *a e d c *b **a *e

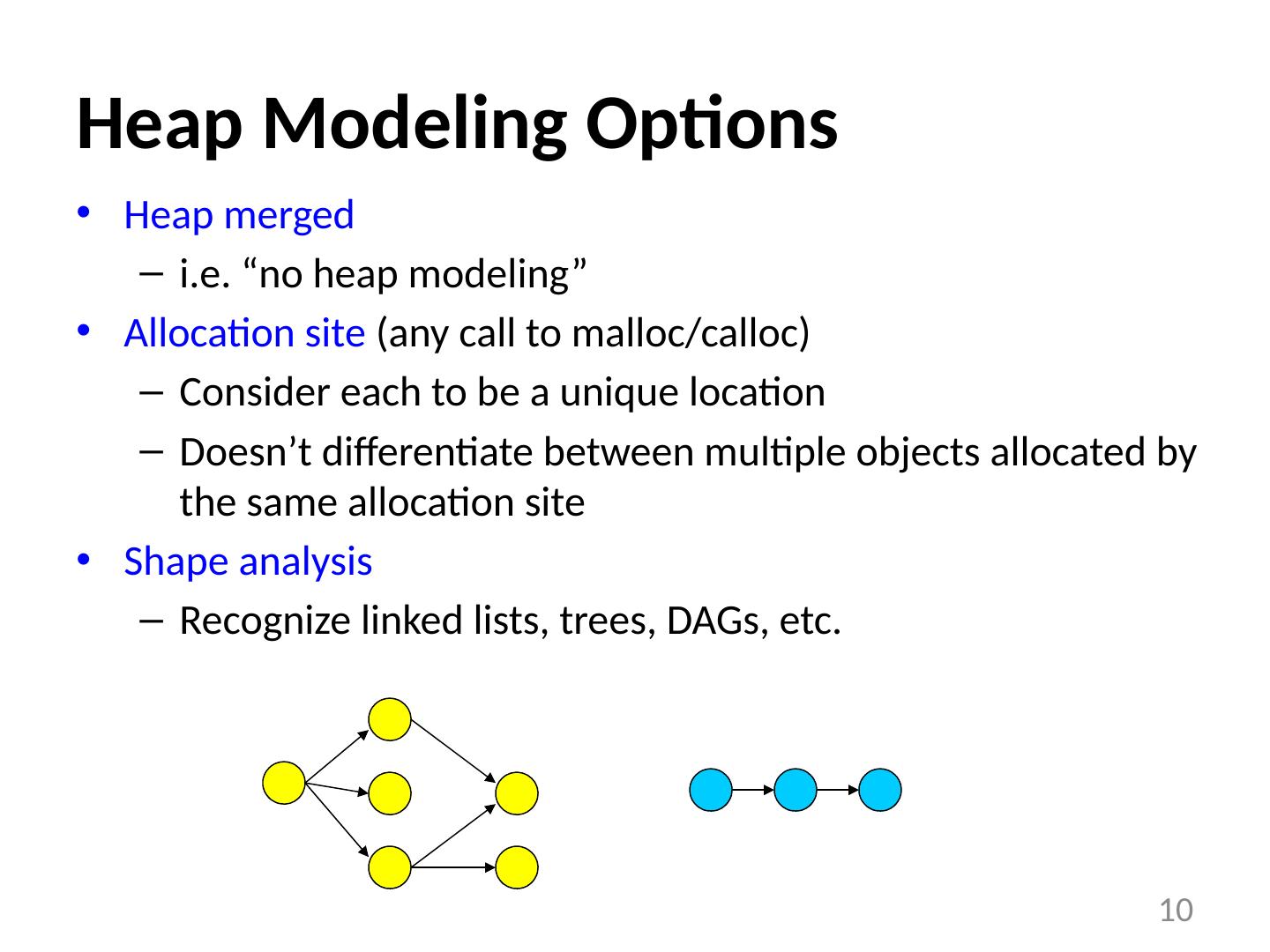
10 .Heap Modeling Options Heap merged i.e. “no heap modeling” Allocation site (any call to malloc / calloc ) Consider each to be a unique location Doesn’t differentiate between multiple objects allocated by the same allocation site Shape analysis Recognize linked lists, trees, DAGs, etc. 10

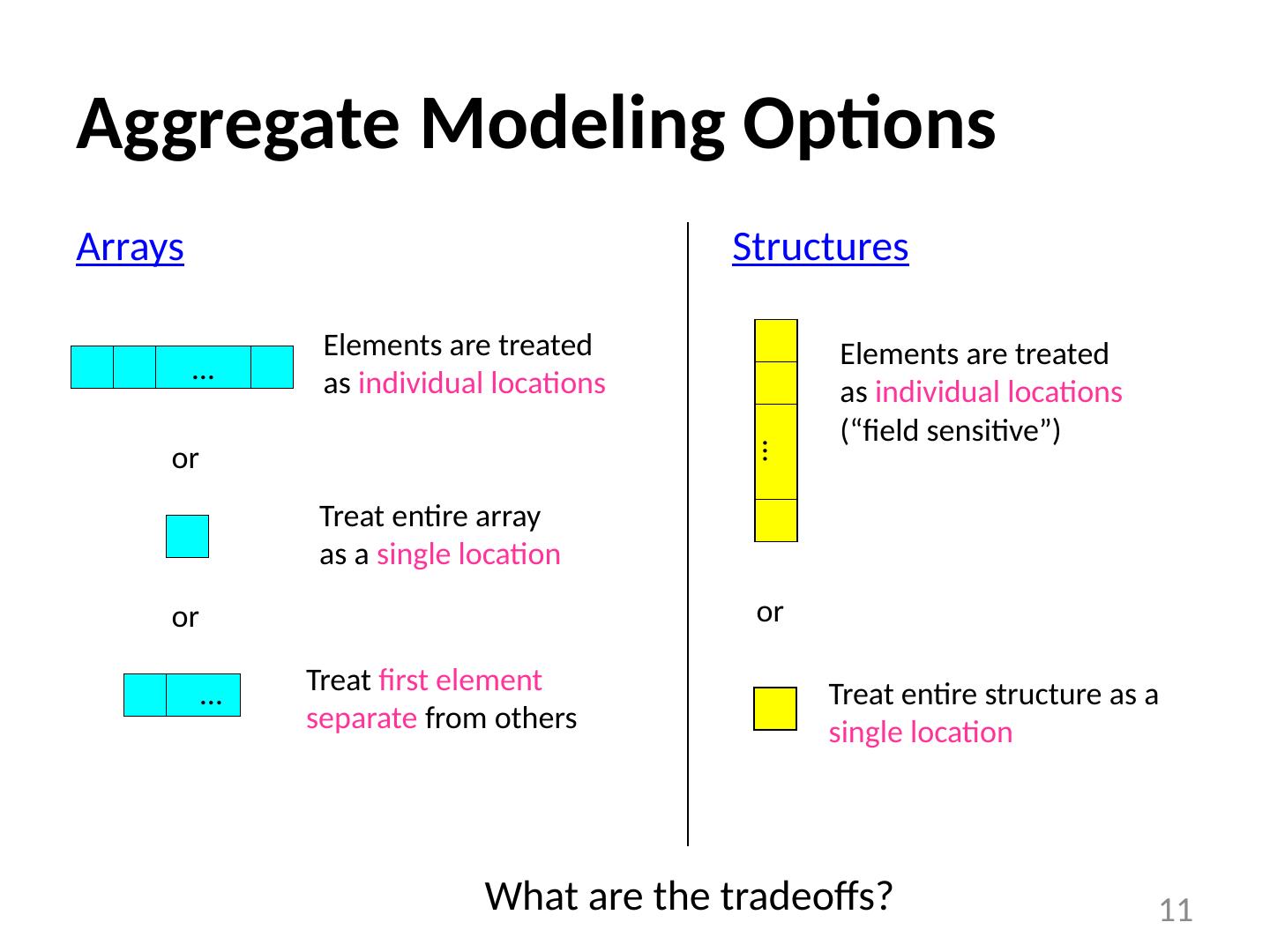
11 .Aggregate Modeling Options Arrays 11 … Elements are treated as individual locations or Treat entire array as a single location or Treat entire structure as a single location … Elements are treated as individual locations (“field sensitive”) Structures or Treat first element separate from others … What are the tradeoffs?

12 .Flow Sensitivity Options Flow insensitive The order of statements doesn’t matter Result of analysis is the same regardless of statement order Uses a single global state to store results as they are computed Not very accurate Flow sensitive The order of the statements matter Need a control flow graph Must store results for each program point Improves accuracy Path sensitive Each path in a control flow graph is considered 12

13 .Flow Sensitivity Example (assuming allocation-site heap modeling) 13 S1: a = malloc (…); S2: b = malloc (…); S3: a = b; S4: a = malloc (…); S5: if(c) a = b; S6: if(!c) a = malloc (…); S7 : … = * a ; Flow Insensitive a S7  Flow S ensitive a S7  Path S ensitive a S7  {heapS1, heapS2, heapS4, heapS6} (order doesn’t matter, union of all possibilities) {heapS2, heapS4, heapS6} (in-order, doesn’t know s5 & s6 are exclusive) {heapS2, heapS6} (in-order, knows s5 & s6 are exclusive)

14 .int a, b, * p ; int main () { S1: f (); S2: p = &a; S3: g (); } Context Sensitivity Options Context insensitive/sensitive whether to consider different calling contexts e.g., what are the possibilities for p at S6 ? 14 int f () { S4: p = &b; S5: g (); } int g () { S6 : … = * p ; } Context Insensitive: Context S ensitive: p S6 => { a,b } Called from S5:p S6 => {b} Called from S3:p S6 => {a}

15 .int a, b, * p ; int main () { S1: f (); S2: p = &a; S3: g (); } Context Sensitivity Options Context insensitive/sensitive whether to consider different calling contexts e.g., what are the possibilities for p at S6 ? 14 int f () { S4: p = &b; S5: g (); } int g () { S6 : … = * p ; } Context Insensitive: Context S ensitive: p S6 => { a,b } Called from S5:p S6 => {b} Called from S3:p S6 => {a}

16 .Address Taken Basic, fast, ultra-conservative algorithm flow-insensitive , context-insensitive often used in production compilers Algorithm : Generate the set of all variables whose addresses are assigned to another variable. Assume that any pointer can potentially point to any variable in that set. Complexity : O(n) - linear in size of program Accuracy : very imprecise 16

17 .Address Taken Example p S5 = 17 T * p , * q , * r ; int main () { S1: p = alloc (T); f (); g (& p ); S4: p = alloc (T); S5 : … = * p ; } void f () { S6: q = alloc (T); g (& q ); S8: r = alloc (T); } g (T ** fp ) { T local; if(…) s9: p = &local; } {heap_S1, p, heap_S4, heap_S6, q, heap_S8, local}

18 .Andersen’s Algorithm Flow-insensitive , context-insensitive , iterative Representation : one points-to graph for entire program each node represents exactly one location For each statement, build the points-to graph: Iterate until graph no longer changes Worst case complexity : O(n 3 ) , where n = program size 18 y = & x y points-to x y = x if x points-to w then y points-to w * y = x if y points-to z and x points-to w then z points-to w y = * x if x points-to z and z points-to w then y points-to w

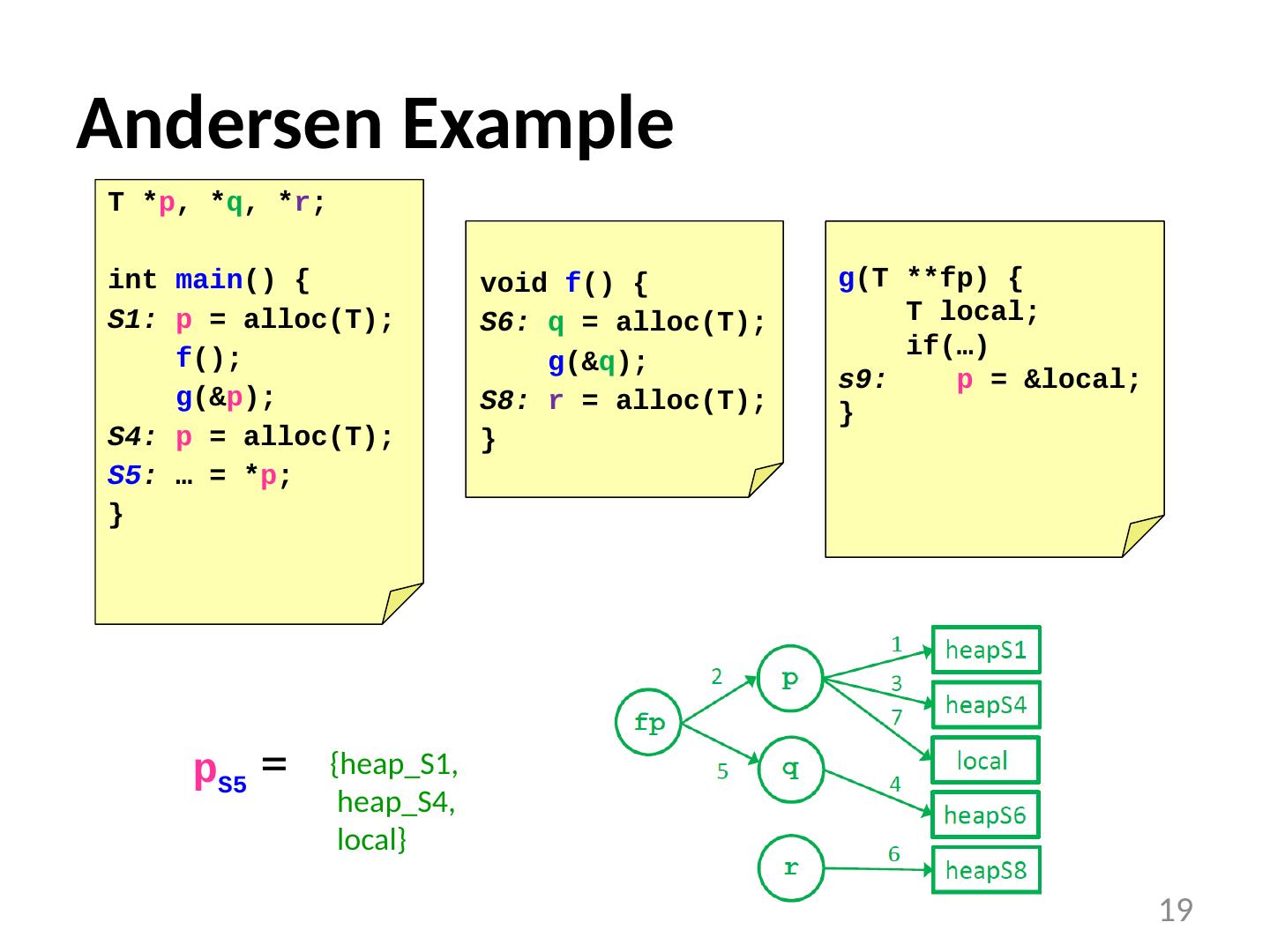
19 .Andersen Example p S5 = 19 T * p , * q , * r ; int main () { S1: p = alloc (T); f (); g (& p ); S4: p = alloc (T); S5 : … = * p ; } void f () { S6: q = alloc (T); g (& q ); S8: r = alloc (T); } g (T ** fp ) { T local; if(…) s9: p = &local; } {heap_S1, heap_S4, local}

20 .Steensgaard’s Algorithm Flow-insensitive , context-insensitive Representation : a compact points-to graph for entire program each node can represent multiple locations but can only point to one other node i.e. every node has a fan-out of 1 or 0 union-find data structure implements fan-out “ unioning ” while finding eliminates need to iterate Worst case complexity : O(n) Precision : less precise than Andersen’s 20

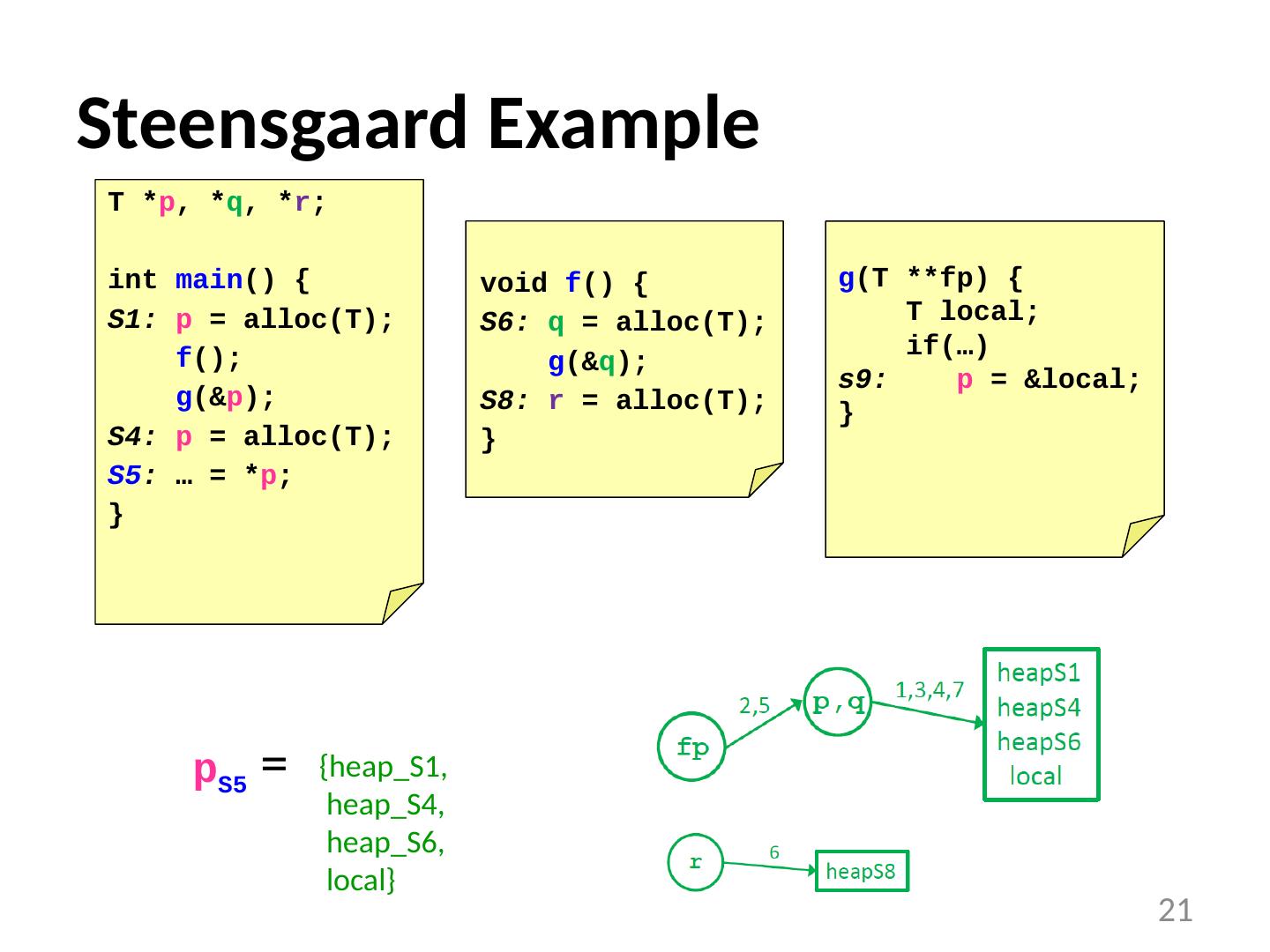
21 .Steensgaard Example p S5 = 21 T * p , * q , * r ; int main () { S1: p = alloc (T); f (); g (& p ); S4: p = alloc (T); S5 : … = * p ; } void f () { S6: q = alloc (T); g (& q ); S8: r = alloc (T); } g (T ** fp ) { T local; if(…) s9: p = &local; } {heap_S1, heap_S4, heap_S6, local}

22 .Example with Flow Sensitivity p S5 = 22 T * p , * q , * r ; int main () { S1: p = alloc (T); f (); g (& p ); S4: p = alloc (T); S5 : … = * p ; } void f () { S6: q = alloc (T); g (& q ); S8: r = alloc (T); } g (T ** fp ) { T local; if(…) s9 : p = &local; } p S9 = {heap_S4} {local, heap_s1}

23 .Pointer Analysis Using BDDs References : “Cloning-based context-sensitive pointer alias analysis using binary decision diagrams” , Whaley and Lam, PLDI 2004 “Symbolic pointer analysis revisited” , Zhu and Calman , PDLI 2004 “Points-to analysis using BDDs” , Berndl et al, PDLI 2003 23

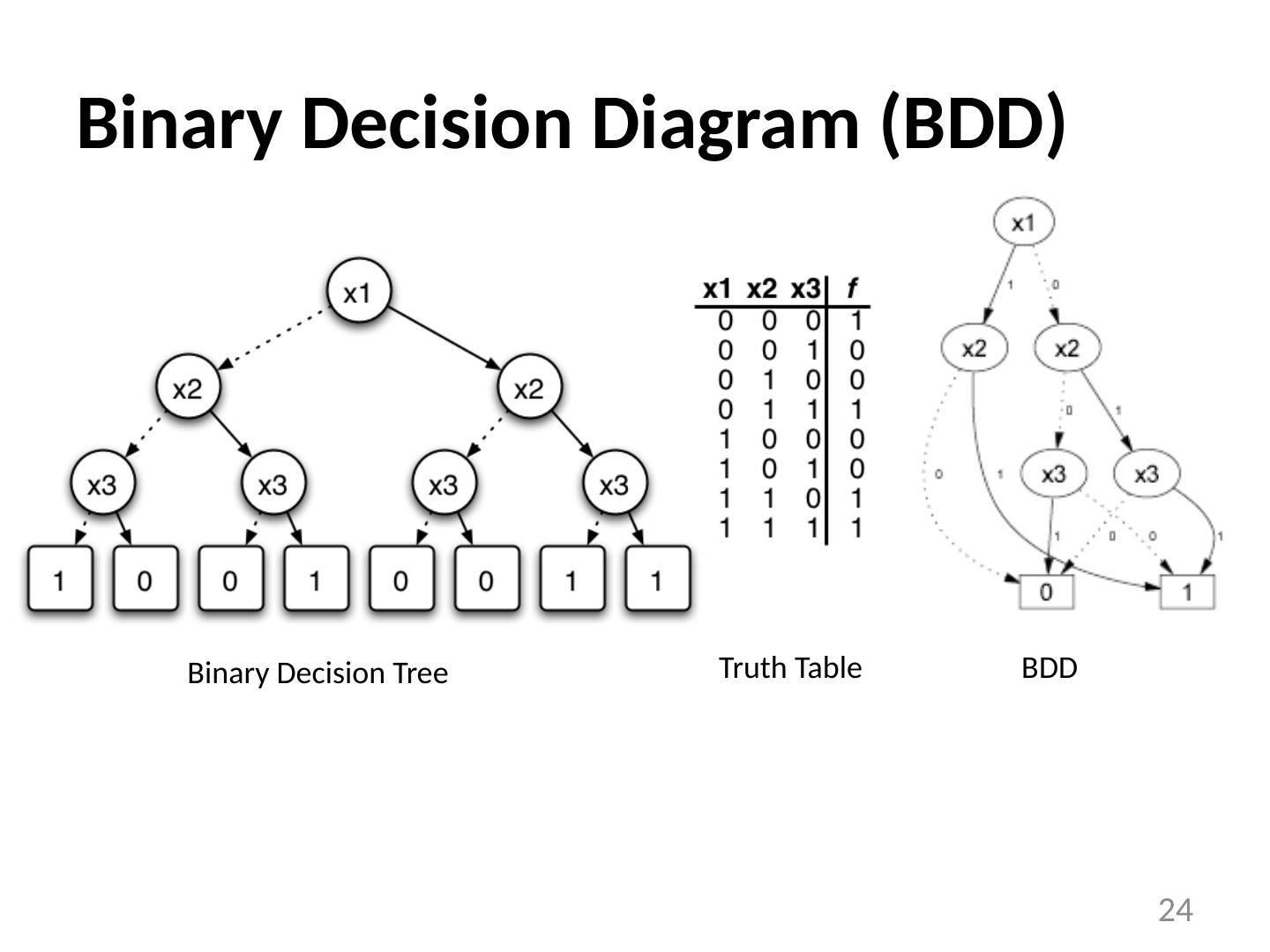
24 .Binary Decision Diagram (BDD) 24 Binary Decision Tree Truth Table BDD

25 .BDD-Based Pointer Analysis Use a BDD to represent transfer functions encode procedure as a function of its calling context compact and efficient representation Perform context-sensitive , inter-procedural analysis similar to dataflow analysis but across the procedure call graph Gives accurate results and scales up to large programs 25

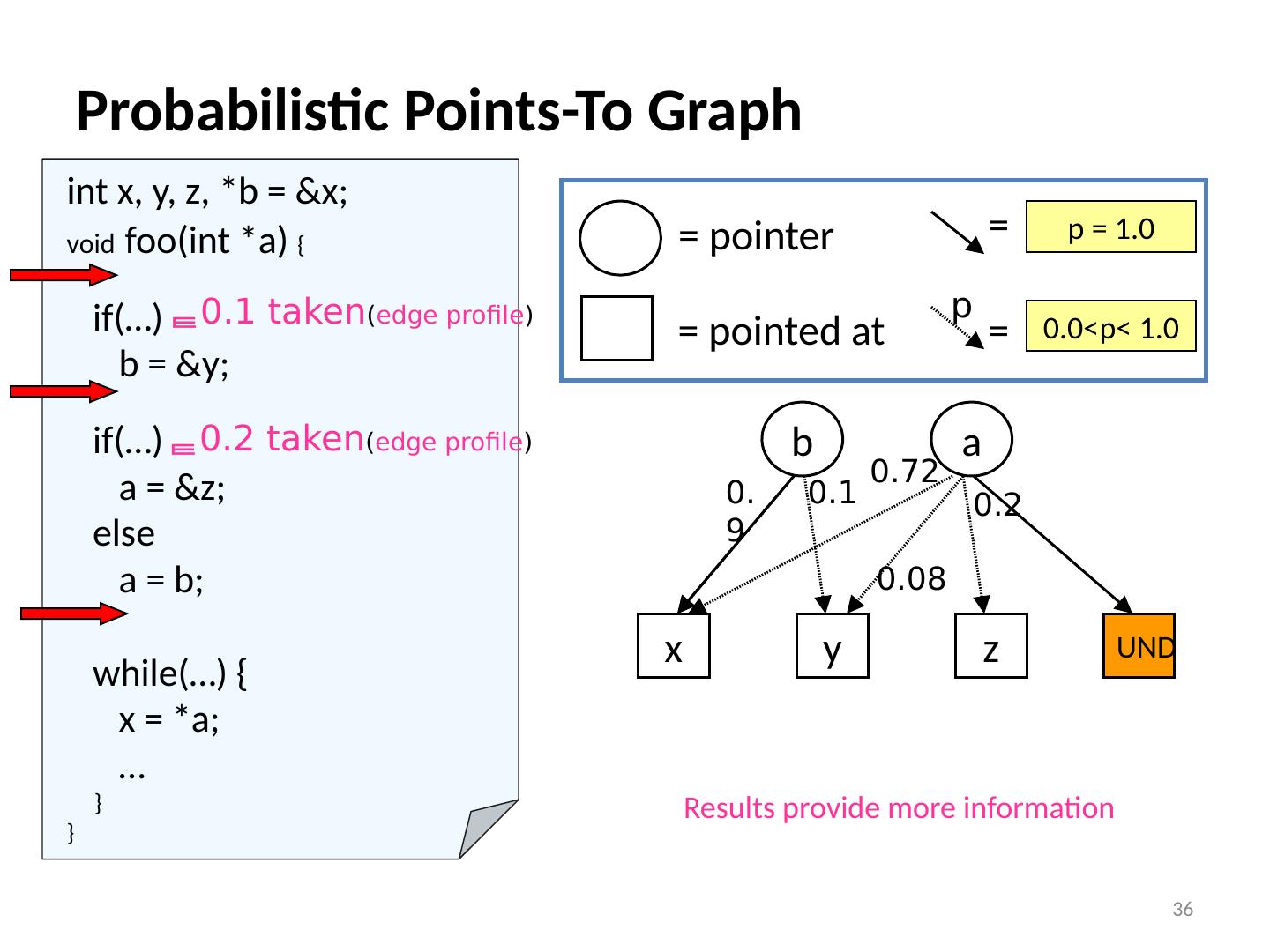
26 .Probabilistic Pointer Analysis References : “A Probabilistic Pointer Analysis for Speculative Optimizations” , DaSilva and Steffan , ASPLOS 2006 “Compiler support for speculative multithreading architecture with probabilistic points-to analysis” , Shen et al., PPoPP 2003 “Speculative Alias Analysis for Executable Code” , Fernandez and Espasa , PACT 2002 “A General Compiler Framework for Speculative Optimizations Using Data Speculative Code Motion” , Dai et al., CGO 2005 “Speculative register promotion using Advanced Load Address Table (ALAT)” , Lin et al., CGO 2003 26

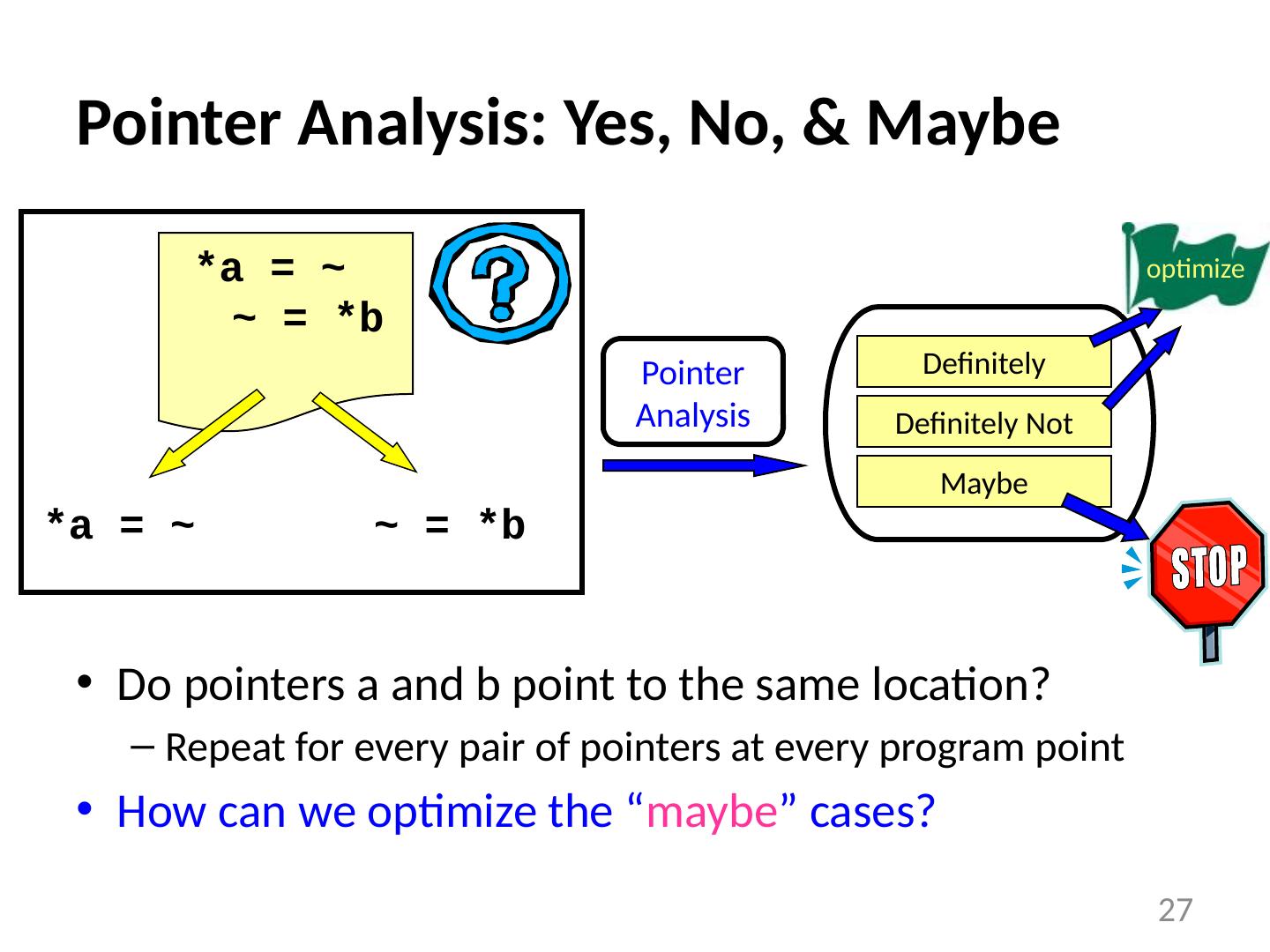
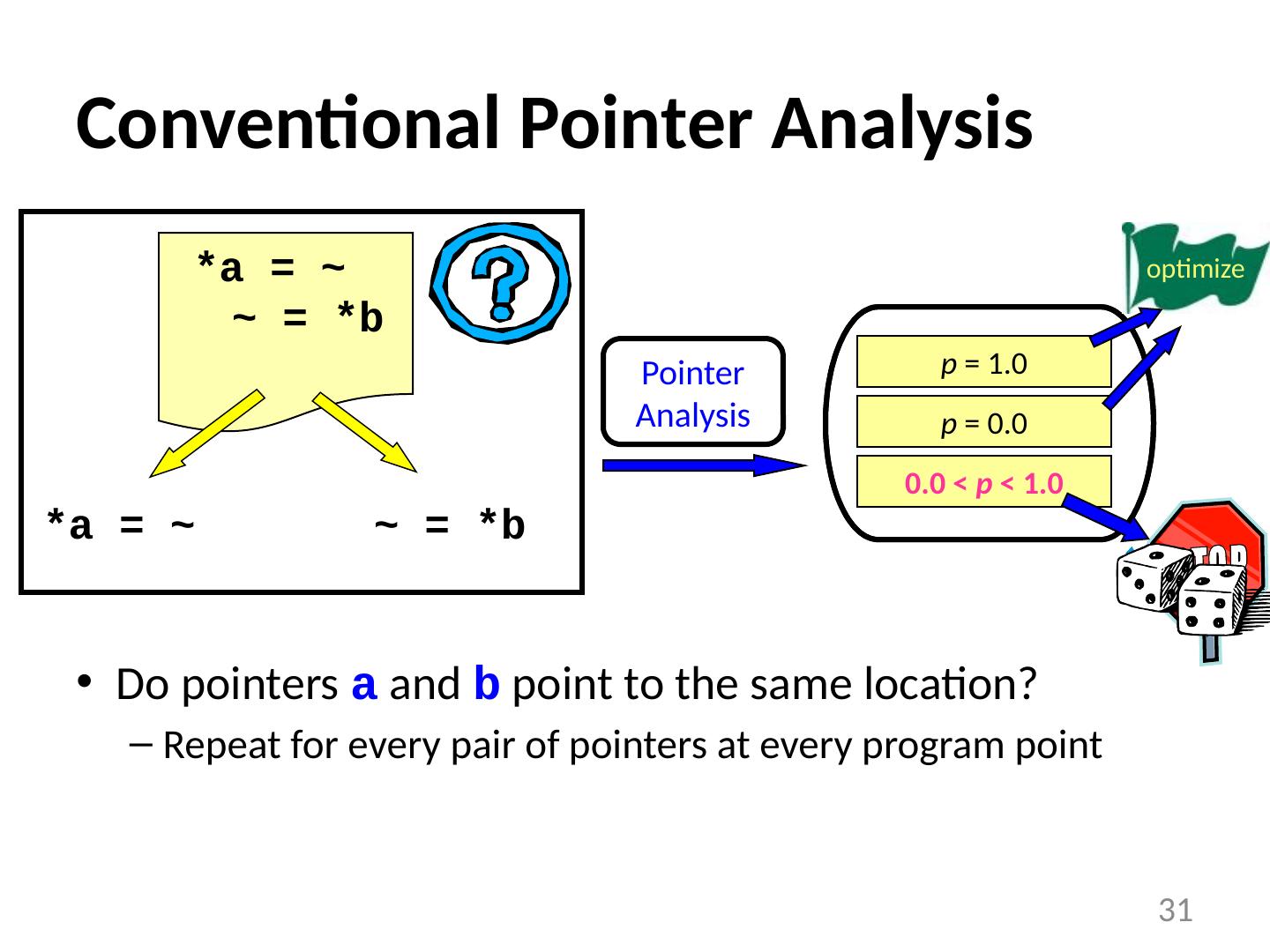
27 .Pointer Analysis: Yes, No, & Maybe Do pointers a and b point to the same location? Repeat for every pair of pointers at every program point How can we optimize the “ maybe ” cases? 27 *a = ~ ~ = *b Definitely Not Definitely Maybe Pointer Analysis optimize *a = ~ ~ = *b

28 .Let’s Speculate Implement a potentially unsafe optimization Verify and Recover if necessary 28 int *a, x; … while(…) { x = *a; … } a is probably loop invariant int *a, x, tmp ; … tmp = *a; while(…) { x = tmp ; … } <verify, recover?>

29 .Data Speculative Optimizations EPIC Instruction sets Support for speculative load/store instructions (e.g., Itanium) Speculative compiler optimizations Dead store elimination, redundancy elimination, copy propagation, strength reduction, register promotion Thread-level speculation (TLS) Hardware and compiler support for speculative parallel threads Transactional programming Hardware and software support for speculative parallel transactions Heavy reliance on detailed profile feedback 29