- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Lecture 6 寄存器分配
展开查看详情
1 .CSC D70: Compiler Optimization Register Allocation Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Phillip Gibbons
2 .Announcements Midterm results Mean: 72% Max: 90%, Min: 54% 2
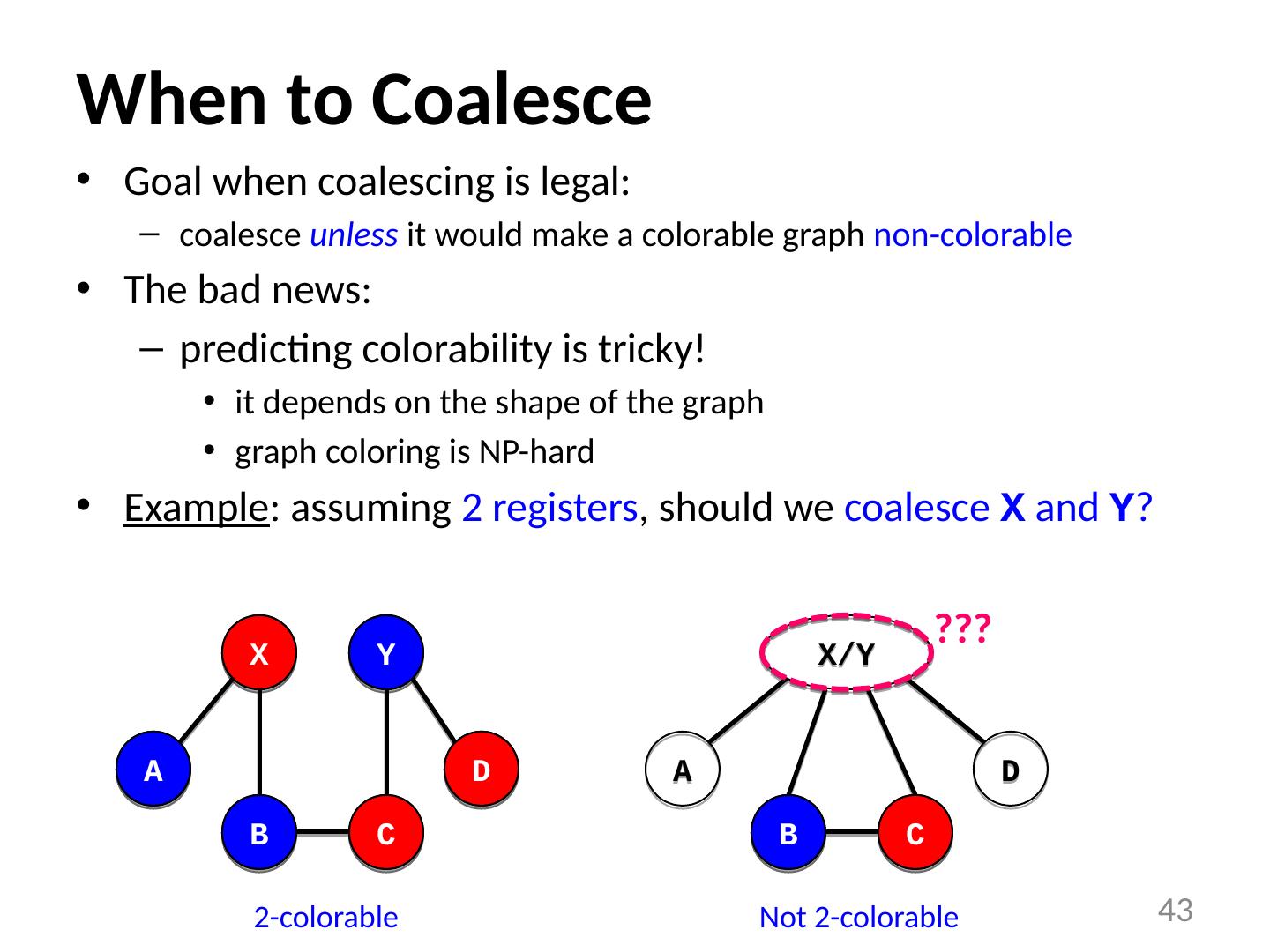
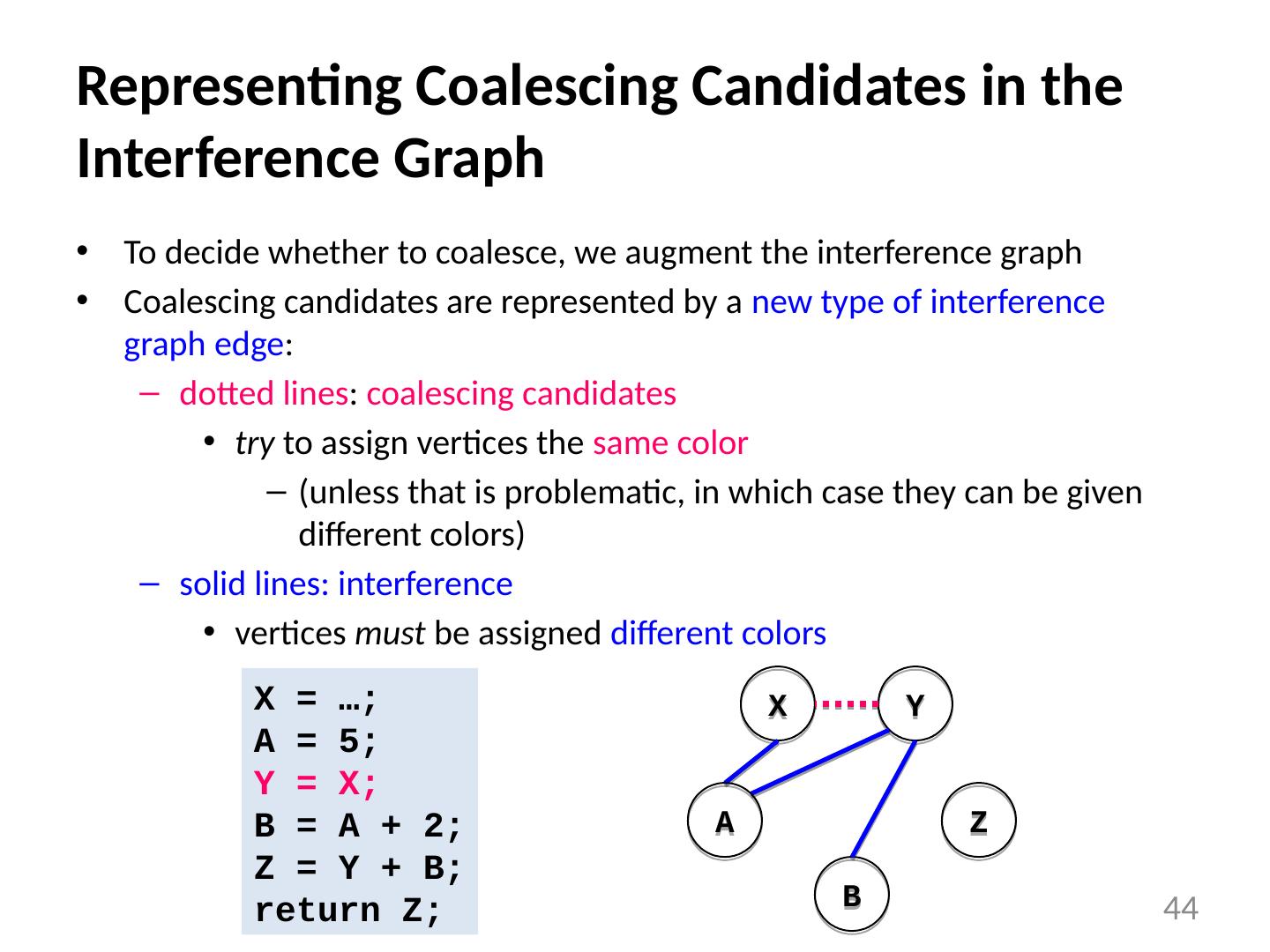
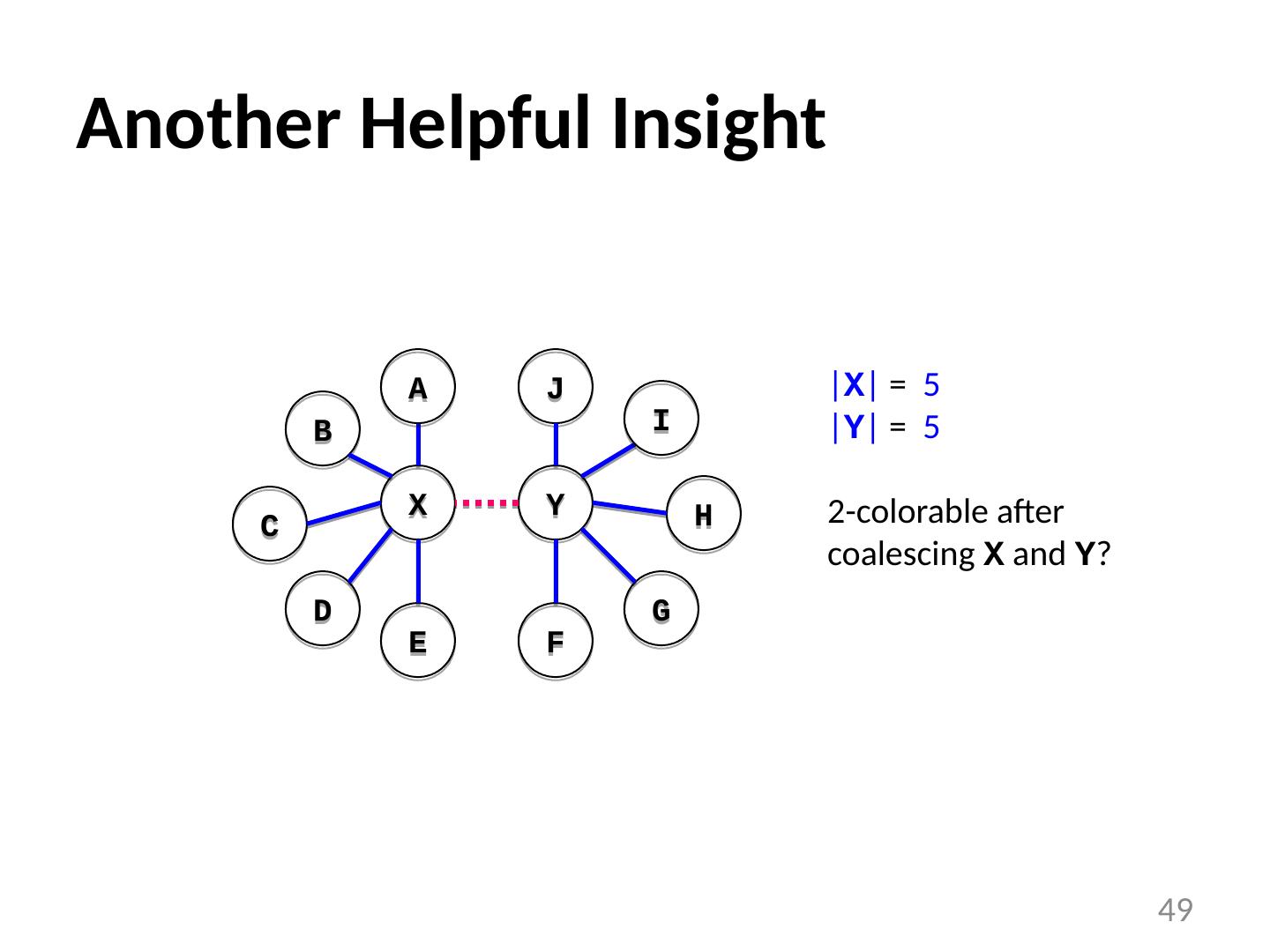
3 .Register Allocation and Coalescing 3 Introduction Abstraction and the Problem Algorithm Spilling Coalescing Reading: ALSU 8.8.4
4 .Motivation Problem Allocation of variables (pseudo-registers) to hardware registers in a procedure A very important optimization! Directly reduces running time (memory access register access) Useful for other optimizations e.g. CSE assumes old values are kept in registers. 4
5 .Goals Find an allocation for all pseudo-registers, if possible. If there are not enough registers in the machine, choose registers to spill to memory 5
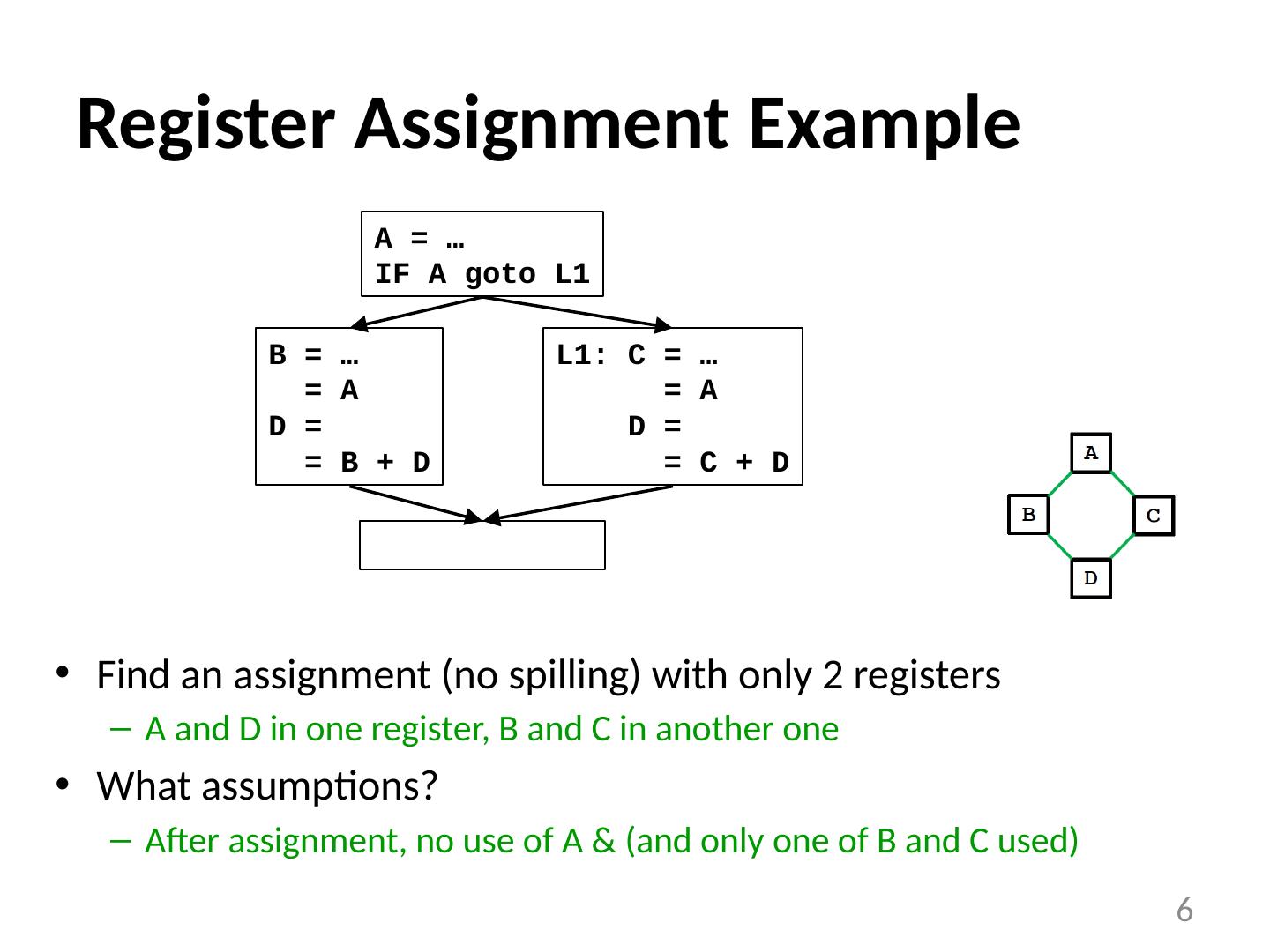
6 .Register Assignment Example 6 B = … = A D = = B + D L1: C = … = A D = = C + D A = … IF A goto L1 Find an assignment (no spilling) with only 2 registers A and D in one register, B and C in another one What assumptions? After assignment, no use of A & (and only one of B and C used)
7 .An Abstraction for Allocation & Assignment Intuitively Two pseudo-registers interfere if at some point in the program they cannot both occupy the same register. Interference graph : an undirected graph, where nodes = pseudo-registers there is an edge between two nodes if their corresponding pseudo-registers interfere What is not represented Extent of the interference between uses of different variables Where in the program is the interference 7
8 .Register Allocation and Coloring A graph is n-colorable if: every node in the graph can be colored with one of the n colors such that two adjacent nodes do not have the same color. Assigning n register (without spilling) = Coloring with n colors assign a node to a register (color) such that no two adjacent nodes are assigned same registers (colors) Is spilling necessary? = Is the graph n-colorable? To determine if a graph is n-colorable is NP-complete, for n>2 Too expensive Heuristics 8
9 .Algorithm Step 1. Build an interference graph refining notion of a node finding the edges Step 2. Coloring use heuristics to try to find an n-coloring Success : colorable and we have an assignment Failure : graph not colorable, or graph is colorable, but it is too expensive to color 9
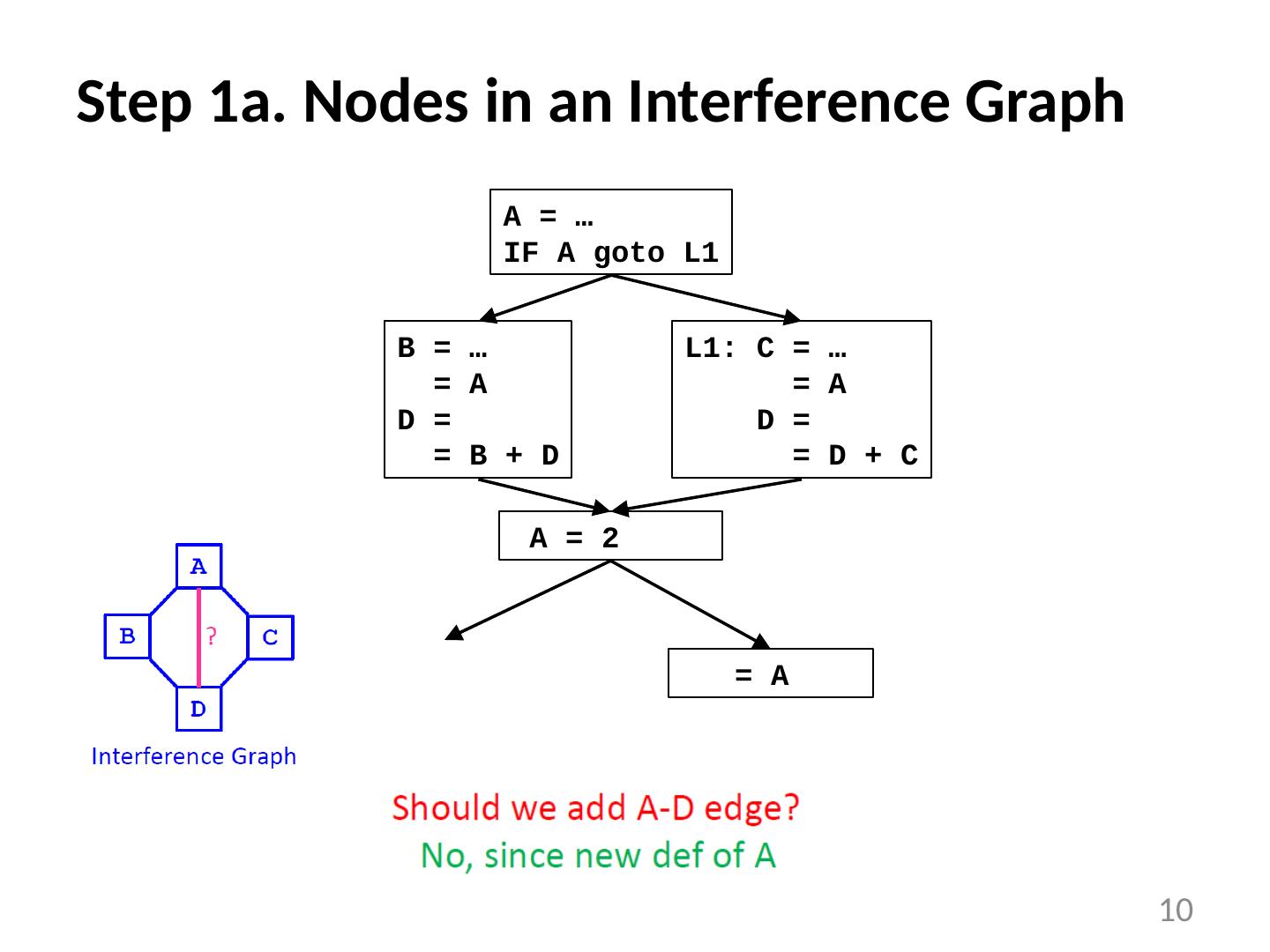
10 .Step 1a. Nodes in an Interference Graph 10 B = … = A D = = B + D L1: C = … = A D = = D + C A = … IF A goto L1 A = 2 = A
11 .Live Ranges and Merged Live Ranges Motivation: to create an interference graph that is easier to color Eliminate interference in a variable’s “dead” zones. Increase flexibility in allocation: can allocate same variable to different registers A live range consists of a definition and all the points in a program in which that definition is live. How to compute a live range? Two overlapping live ranges for the same variable must be merged 11 a = … a = … … = a
12 .Merge 12 Example (Revisited) A = ... (A 1 ) IF A goto L1 L1: C = ... (C 1 ) = A D = ... (D 1 ) B = ... (B 1 ) = A D = B (D 2 ) A = 2 (A 2 ) = A ret D {} {} {A} {A 1 } {A} {A 1 } {A} {A 1 } {A,B} {A 1 ,B 1 } {B} {A 1 ,B 1 } {D} {A 1 ,B 1 ,D 2 } Live Variables Reaching Definitions {A} {A 1 } {A,C} {A 1 ,C 1 } {C} {A 1 ,C 1 } {D} {A 1 ,C 1 ,D 1 } {D} {A 1 ,B 1 ,C 1 ,D 1 ,D 2 } {A,D} {A 2 ,B 1 ,C 1 ,D 1 ,D 2 } {A,D} {A 2 ,B 1 ,C 1 ,D 1 ,D 2 } {D} {A 2 ,B 1 ,C 1 ,D 1 ,D 2 }
13 .Merging Live Ranges Merging definitions into equivalence classes Start by putting each definition in a different equivalence class Then, for each point in a program: if ( i ) variable is live , and (ii) there are multiple reaching definitions for the variable , then: merge the equivalence classes of all such definitions into one equivalence class (Sound familiar?) From now on, refer to merged live ranges simply as live ranges merged live ranges are also known as “ webs ” 13
14 .SSA Revisited: What Happens to Functions Now we see why it is unnecessary to “implement” a function functions and SSA variable renaming simply turn into merged live ranges When you encounter: X 4 = (X 1 , X 2 , X 3 ) merge X 1 , X 2 , X 3 , and X 4 into the same live range delete the function Now you have effectively converted back out of SSA form 14
15 .Step 1b. Edges of Interference Graph Intuitively : Two live ranges (necessarily of different variables) may interfere if they overlap at some point in the program . Algorithm: At each point in the program: enter an edge for every pair of live ranges at that point . An optimized definition & algorithm for edges: Algorithm: check for interference only at the start of each live range Faster Better quality 15
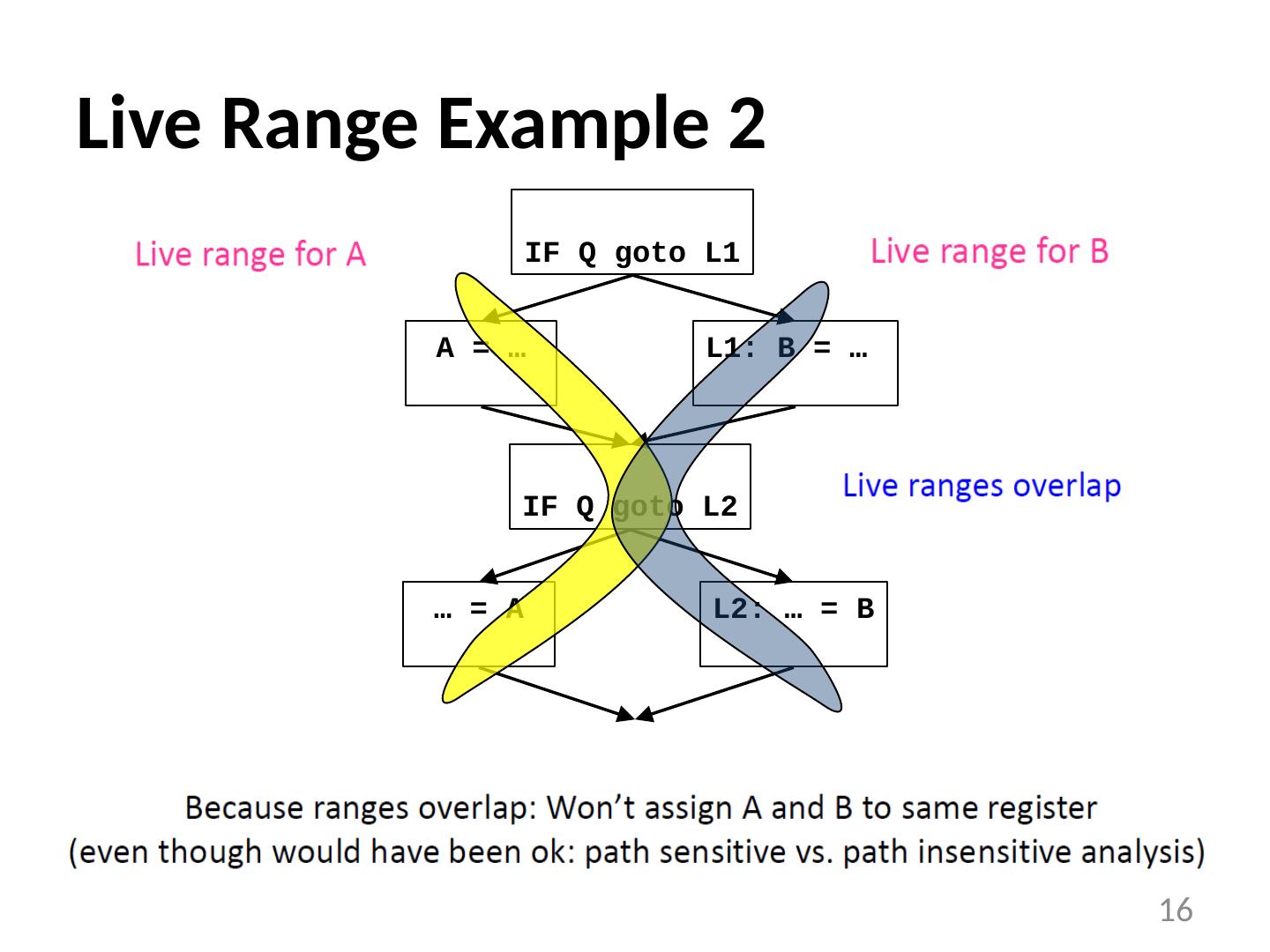
16 .Live Range Example 2 16 A = … L1: B = … IF Q goto L1 IF Q goto L2 L2: … = B … = A
17 .Step 2. Coloring Reminder: coloring for n > 2 is NP-complete Observations : a node with degree < n can always color it successfully, given its neighbors’ colors a node with degree = n can only color if at least two neighbors share same color a node with degree > n maybe, not always 17
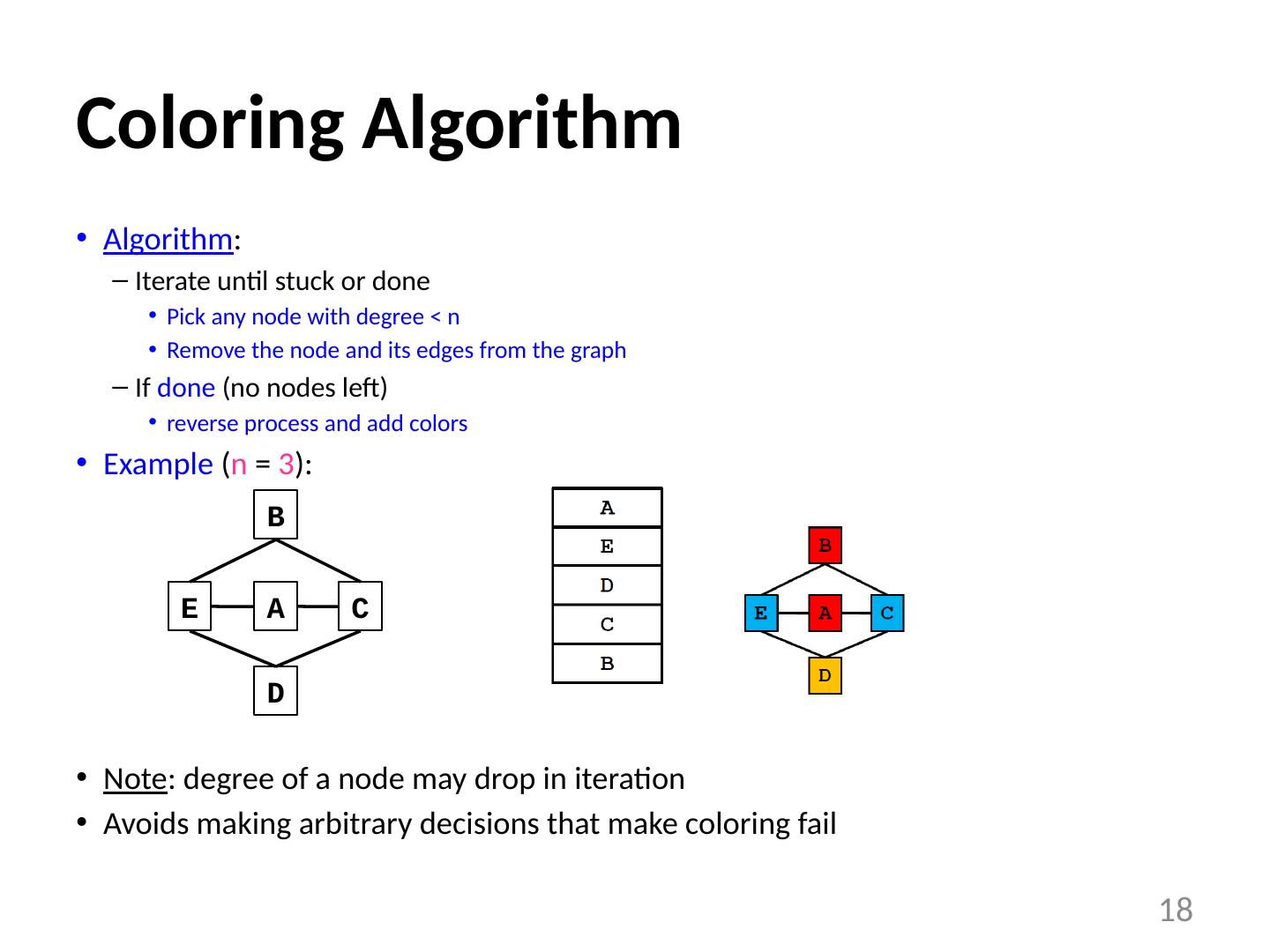
18 .Coloring Algorithm Algorithm : Iterate until stuck or done Pick any node with degree < n Remove the node and its edges from the graph If done (no nodes left) reverse process and add colors Example ( n = 3 ): Note : degree of a node may drop in iteration Avoids making arbitrary decisions that make coloring fail 18 B C E A D
19 .More details 19
20 .What Does Coloring Accomplish? Done : colorable, also obtained an assignment Stuck : colorable or not? 20 B C E A D
21 .Extending Coloring: Design Principles A pseudo-register is Colored successfully : allocated a hardware register Not colored : left in memory Objective function Cost of an uncolored node: proportional to number of uses/definitions (dynamically) estimate by its loop nesting Objective: minimize sum of cost of uncolored nodes Heuristics Benefit of spilling a pseudo-register: increases colorability of pseudo-registers it interferes with can approximate by its degree in interference graph Greedy heuristic spill the pseudo-register with lowest cost-to-benefit ratio , whenever spilling is necessary 21
22 .Spilling to Memory CISC architectures can operate on data in memory directly memory operations are slower than register operations RISC architectures machine instructions can only apply to registers Use must first load data from memory to a register before use Definition must first compute RHS in a register store to memory afterwards Even if spilled to memory, needs a register at time of use/definition 22
23 .23 Chaitin: Coloring and Spilling Identify spilling Build interference graph Iterate until there are no nodes left If there exists a node v with less than n neighbor place v on stack to register allocate else v = node with highest degree-to-cost ratio mark v as spilled remove v and its edges from graph Spilling may require use of registers; change interference graph While there is spilling rebuild interference graph and perform step above Assign registers While stack is not empty Remove v from stack Reinsert v and its edges into the graph Assign v a color that differs from all its neighbors
24 .Spilling What should we spill? Something that will eliminate a lot of interference edges Something that is used infrequently Maybe something that is live across a lot of calls? One Heuristic: spill cheapest live range (aka “web”) Cost = [(# defs & uses)*10 loop-nest-depth ]/degree 24
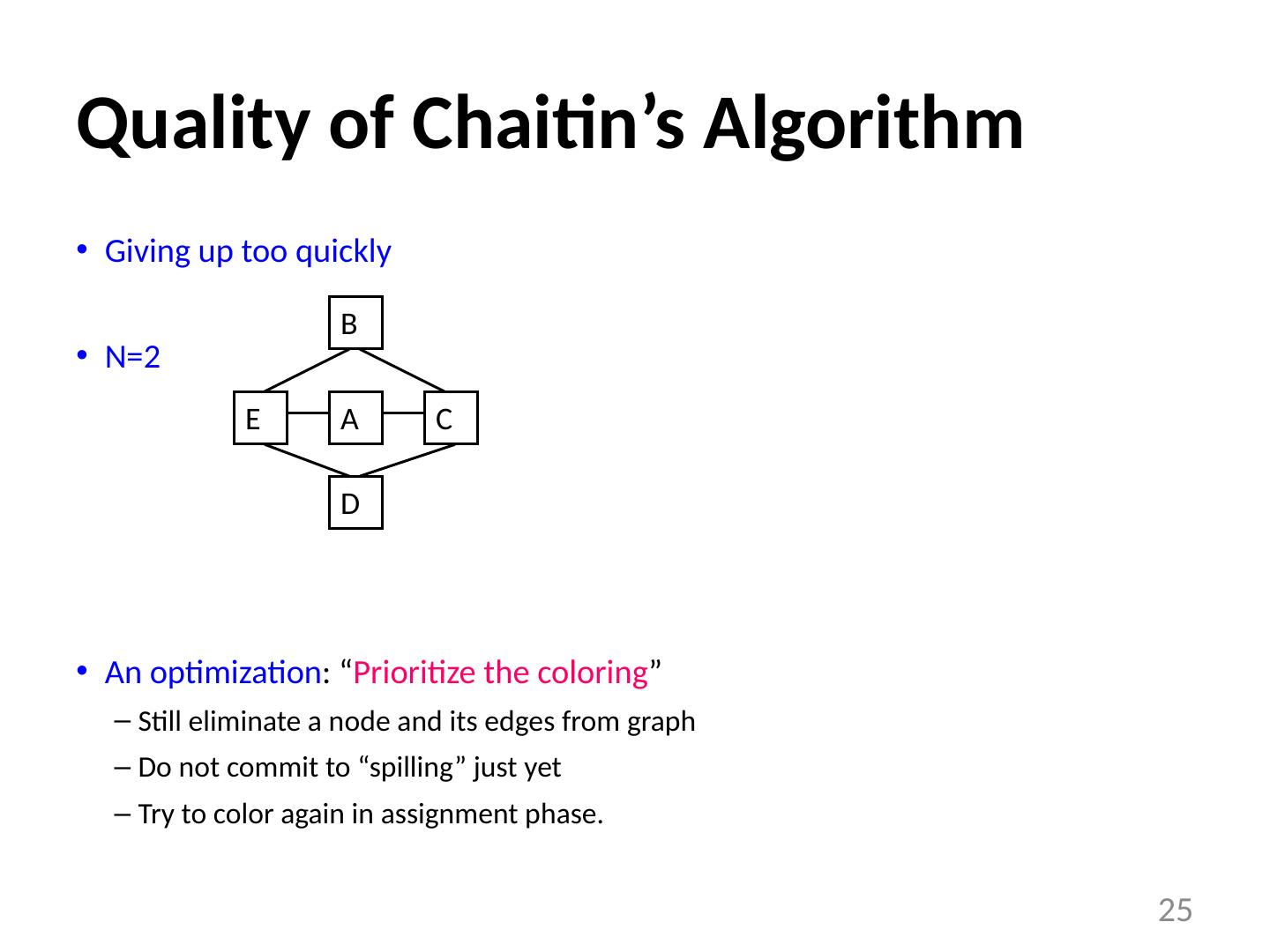
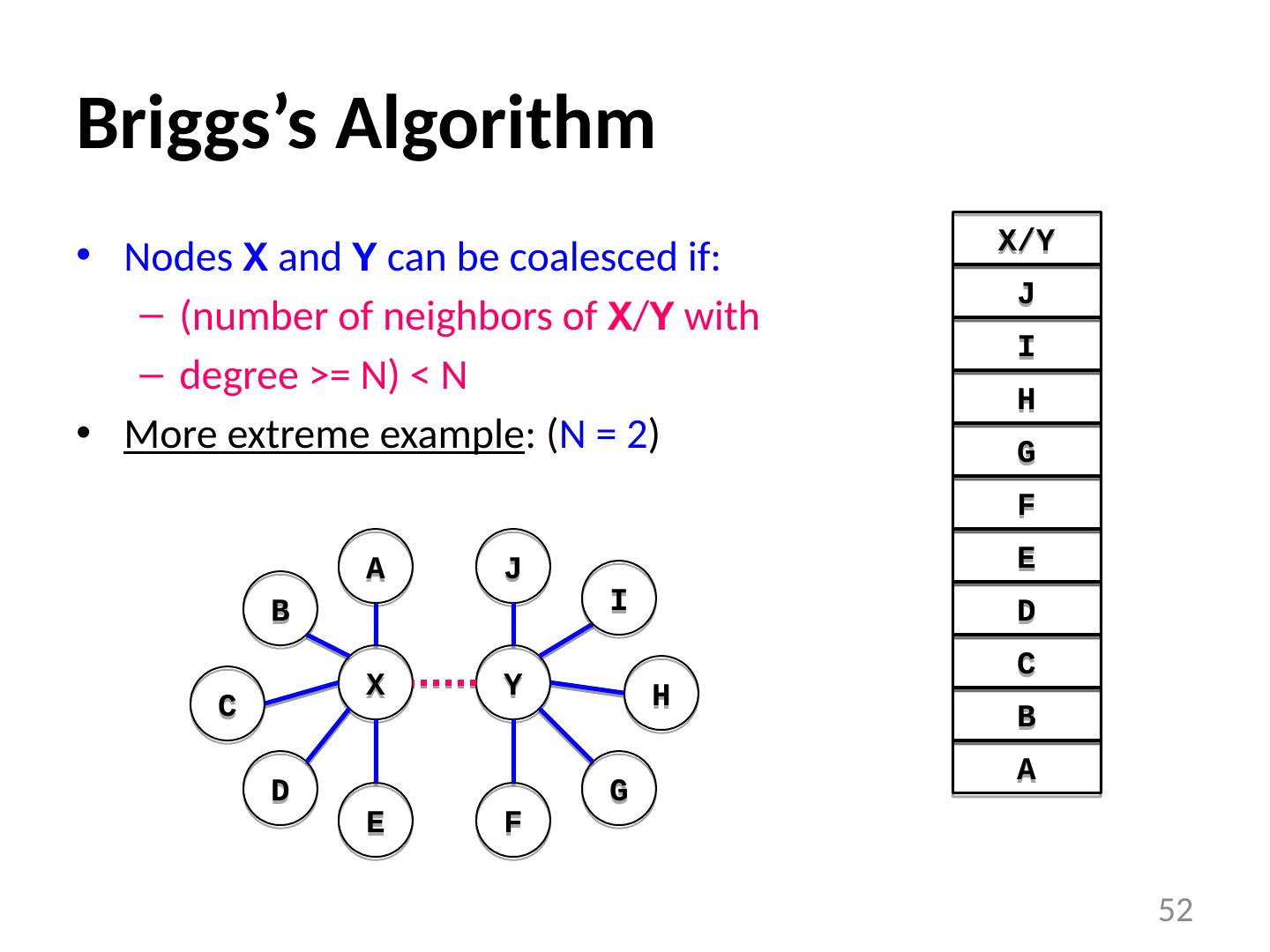
25 .Quality of Chaitin’s Algorithm Giving up too quickly N=2 An optimization : “ Prioritize the coloring ” Still eliminate a node and its edges from graph Do not commit to “spilling” just yet Try to color again in assignment phase. 25 B A C D E
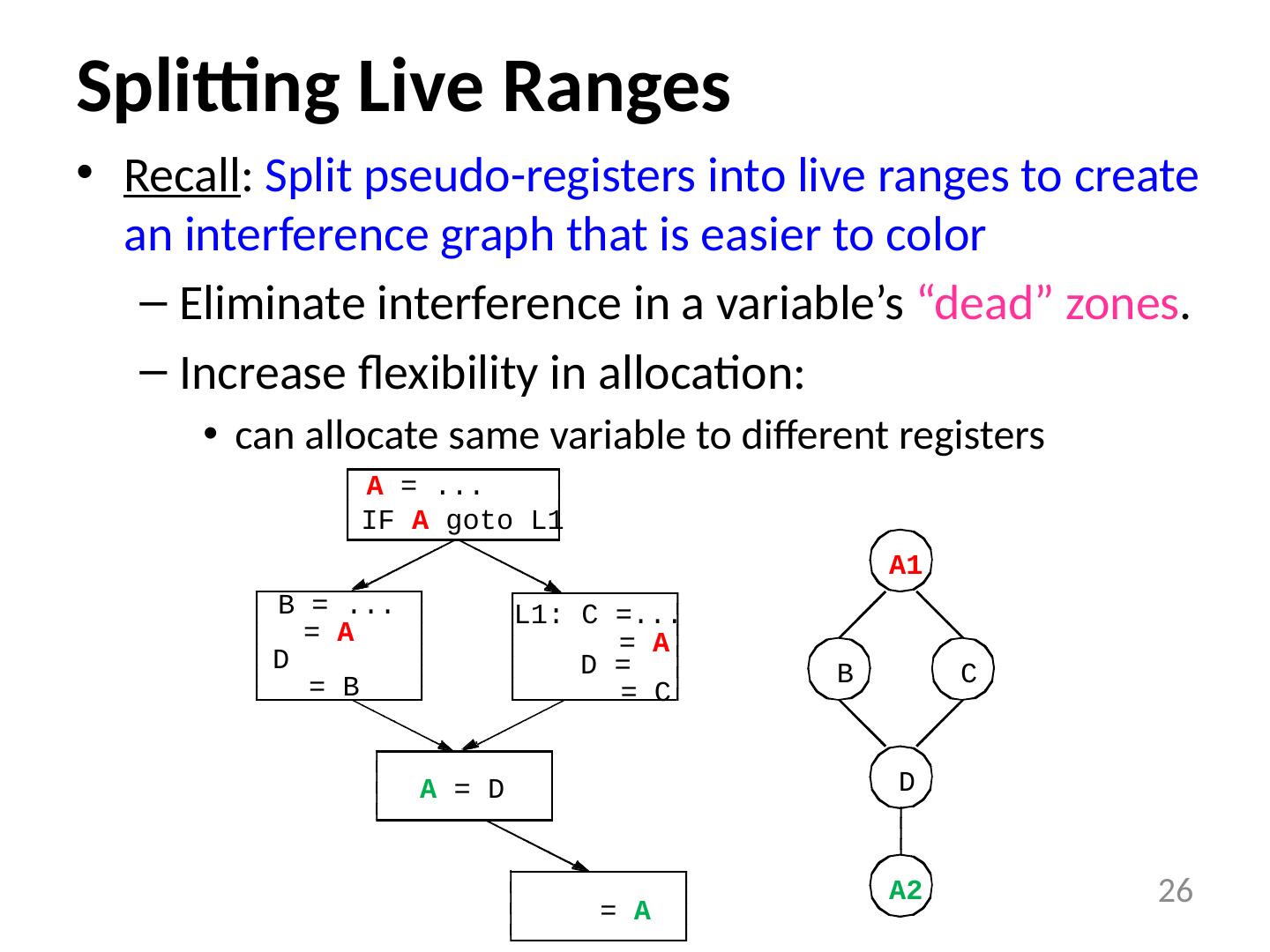
26 .Splitting Live Ranges Recall : Split pseudo-registers into live ranges to create an interference graph that is easier to color Eliminate interference in a variable’s “dead” zones . Increase flexibility in allocation: can allocate same variable to different registers 26 IF A goto L1 A = ... B = ... L1: C =... = A D = A D = A = D = A A1 C B D A2 = B = C
27 .Insight Split a live range into smaller regions (by paying a small cost) to create an interference graph that is easier to color Eliminate interference in a variable’s “nearly dead” zones . Cost : Memory loads and stores Load and store at boundaries of regions with no activity # active live ranges at a program point can be > # registers Can allocate same variable to different registers Cost : Register operations a register copy between regions of different assignments # active live ranges cannot be > # registers 27
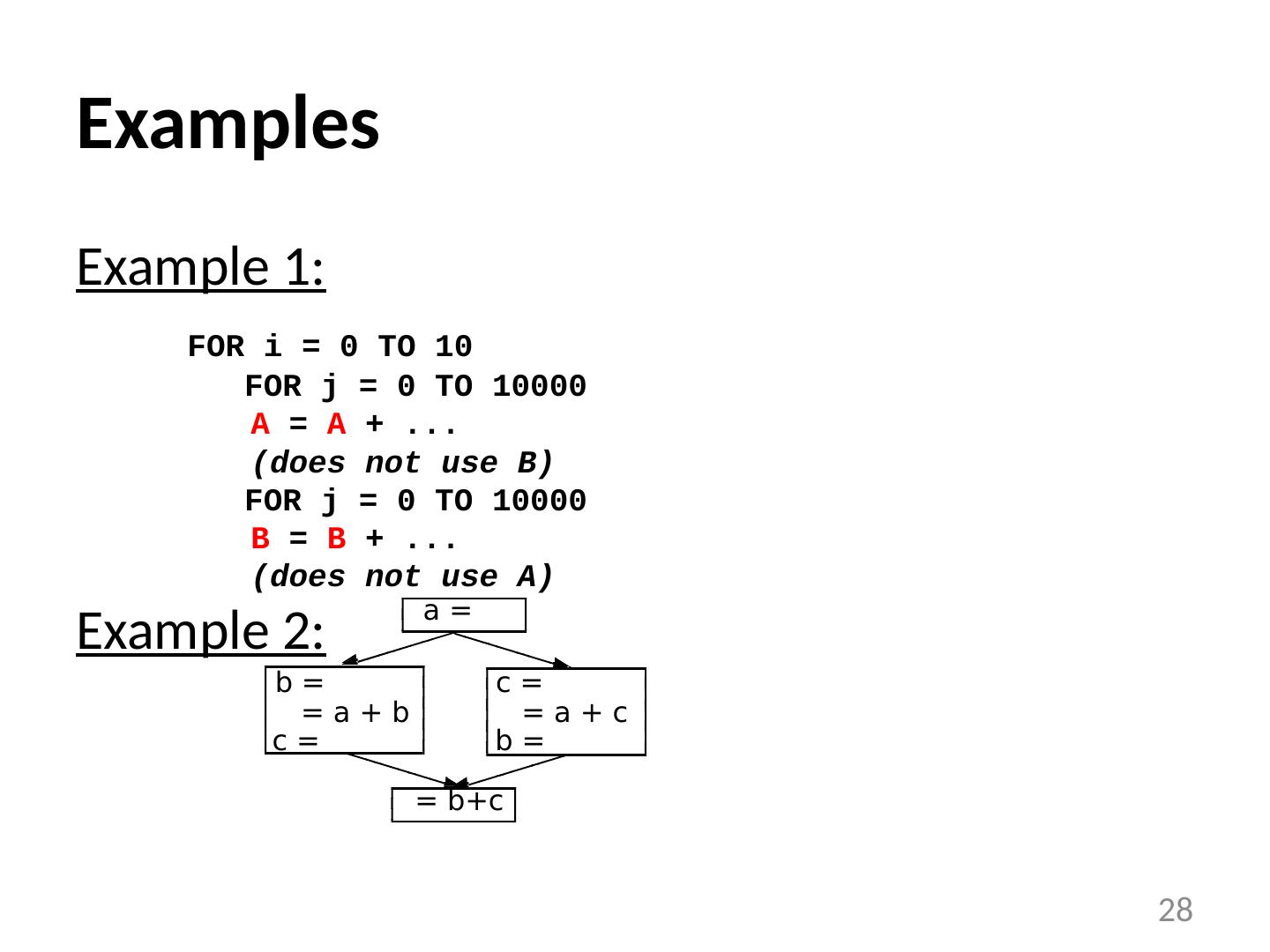
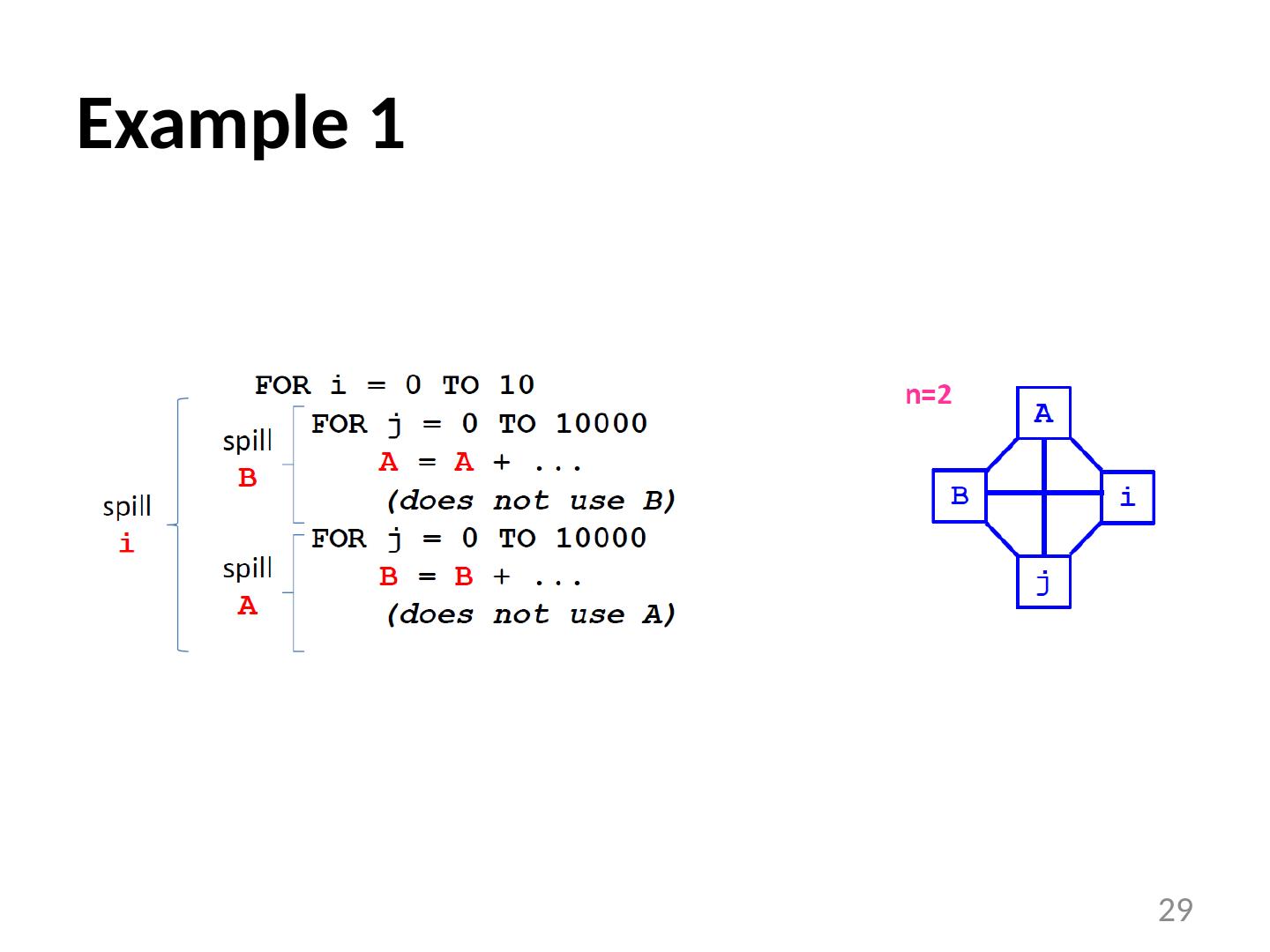
28 .28 Examples Example 1: FOR i = 0 TO 10 FOR j = 0 TO 10000 A = A + ... (does not use B) FOR j = 0 TO 10000 B = B + ... (does not use A) Example 2: a = b = = a + b c = = b+c b = c = = a + c
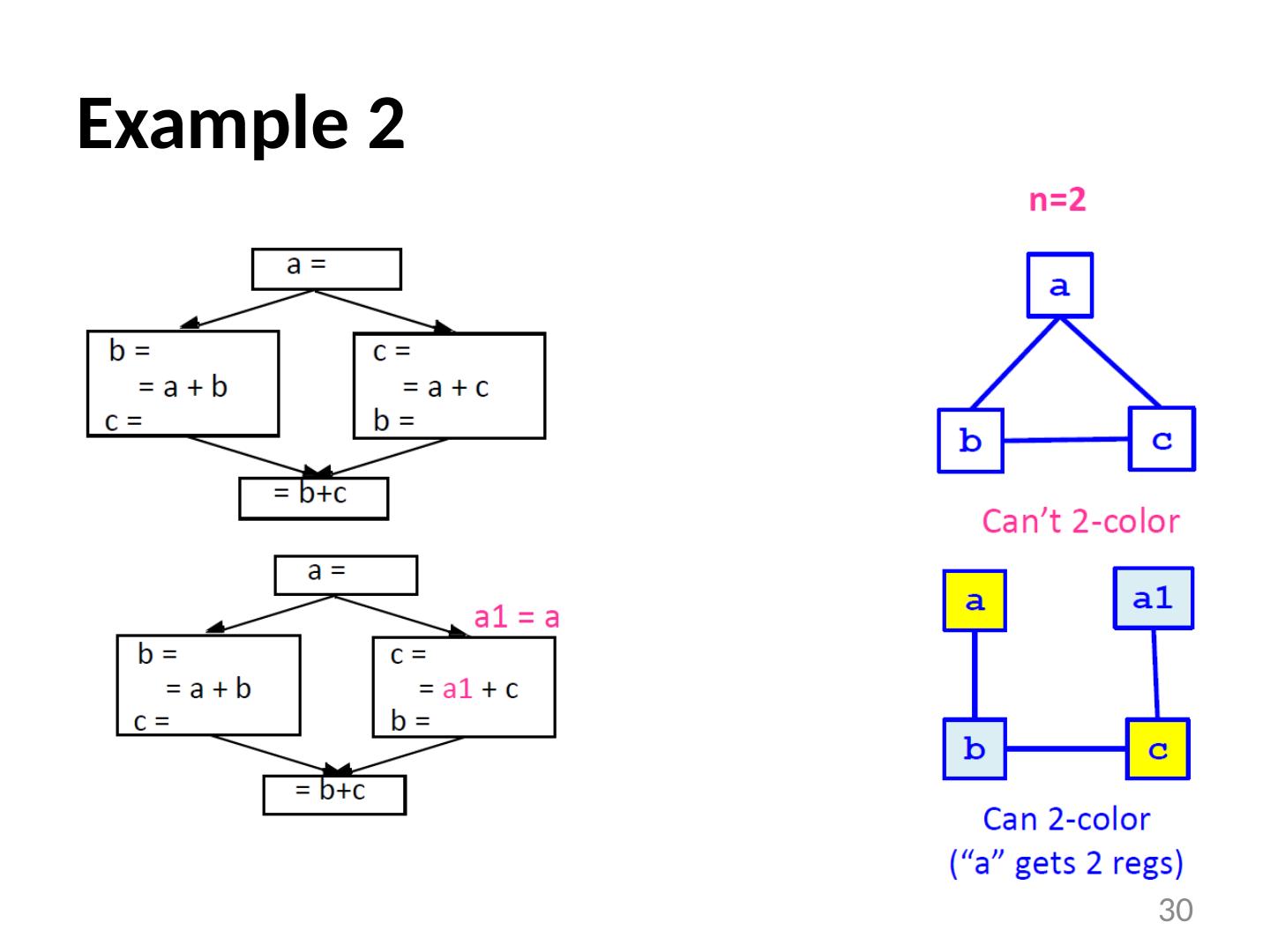
29 .Example 1 29