Lecture 5 LICM and Strength Reduction

1 .CSC D70: Compiler Optimization LICM: Loop Invariant Code Motion Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Phillip Gibbons

2 .Announcements No lecture next week Traveling to SysML conference (Stanford, CA) Assignment 2 is out (due March 8) Midterm is March 1 st (during the class) 2

3 .Refreshing: Finding Loops 3

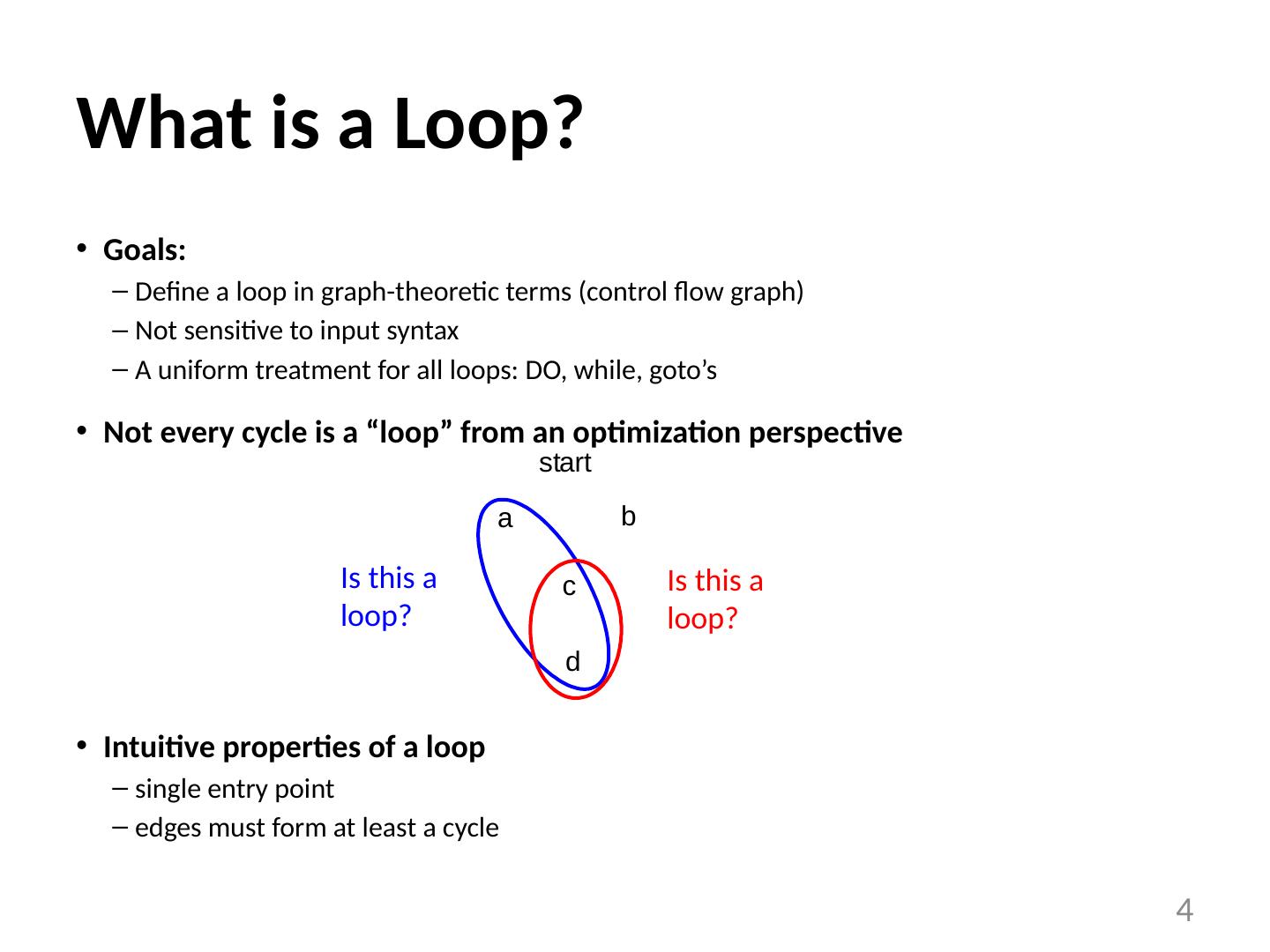
4 .What is a Loop? Goals: Define a loop in graph-theoretic terms (control flow graph) Not sensitive to input syntax A uniform treatment for all loops: DO, while, goto’s Not every cycle is a “loop” from an optimization perspective Intuitive properties of a loop single entry point edges must form at least a cycle 4 Is this a loop? Is this a loop?

5 .Formal Definitions Dominators Node d dominates node n in a graph ( d dom n ) if every path from the start node to n goes through d Dominators can be organized as a tree a -> b in the dominator tree iff a immediately dominates b 5

6 .Natural Loops Definitions Single entry-point: header a header dominates all nodes in the loop A back edge is an arc whose head dominates its tail (tail -> head) a back edge must be a part of at least one loop The natural loop of a back edge is the smallest set of nodes that includes the head and tail of the back edge , and has no predecessors outside the set , except for the predecessors of the header. 6

7 .Algorithm to Find Natural Loops Find the dominator relations in a flow graph Identify the back edges Find the natural loop associated with the back edge 7

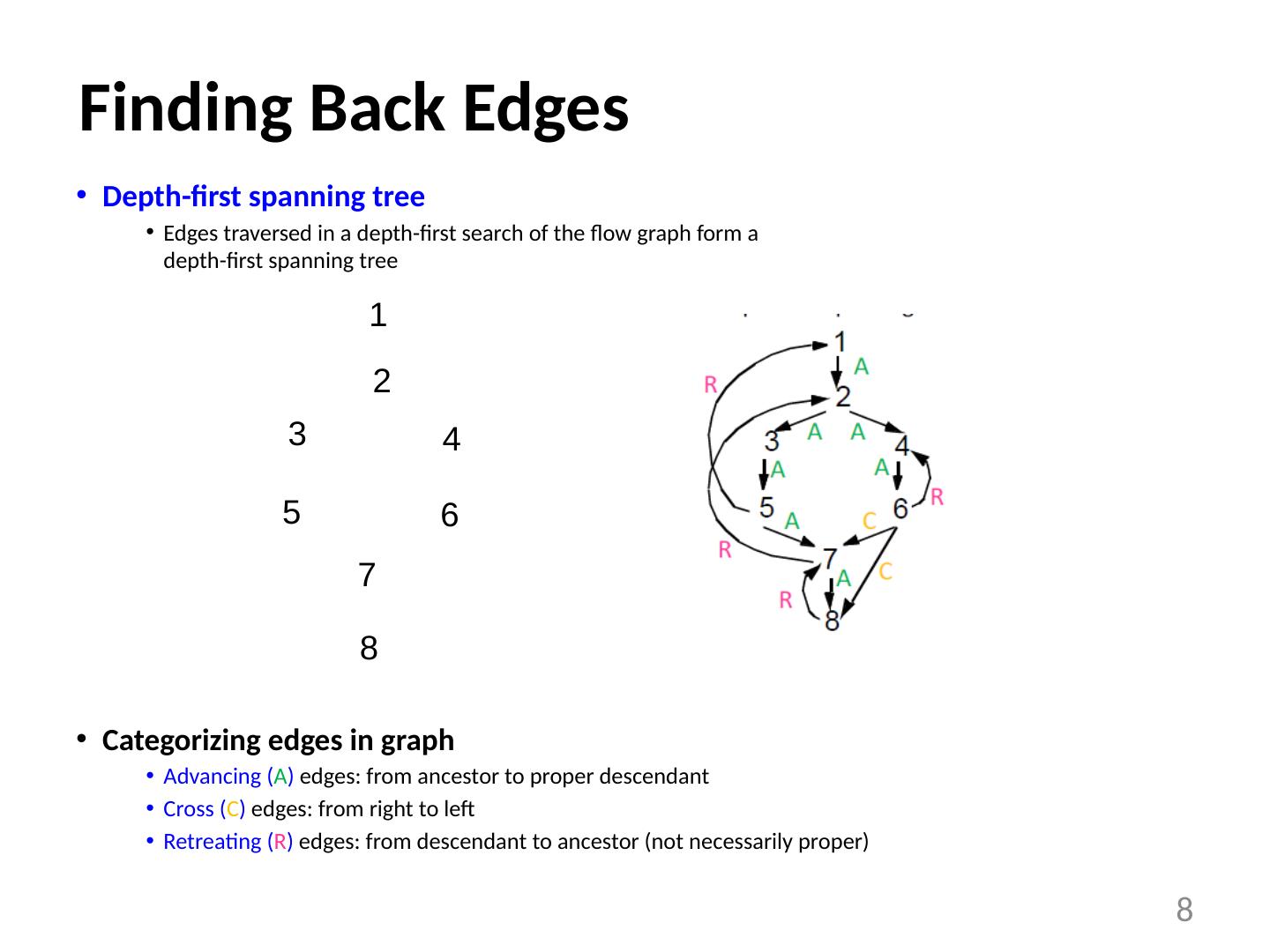
8 .Finding Back Edges Depth-first spanning tree Edges traversed in a depth-first search of the flow graph form a depth-first spanning tree Categorizing edges in graph Advancing ( A ) edges: from ancestor to proper descendant Cross ( C ) edges: from right to left Retreating ( R ) edges: from descendant to ancestor (not necessarily proper) 8

9 .Back Edges Definition Back edge : t->h, h dominates t Relationships between graph edges and back edges Algorithm Perform a depth first search For each retreating edge t->h, check if h is in t’s dominator list Most programs (all structured code, and most GOTO programs) have reducible flow graphs retreating edges = back edges 9

10 .Constructing Natural Loops The natural loop of a back edge is the smallest set of nodes that includes the head and tail of the back edge, and has no predecessors outside the set, except for the predecessors of the header. Algorithm delete h from the flow graph find those nodes that can reach t (those nodes plus h form the natural loop of t -> h ) 10

11 .Inner Loops If two loops do not have the same header: they are either disjoint, or one is entirely contained (nested within) the other inner loop: one that contains no other loop. If two loops share the same header: Hard to tell which is the inner loop Combine as one 11

12 .Preheader Optimizations often require code to be executed once before the loop Create a preheader basic block for every loop 12

13 .Finding Loops: Summary Define loops in graph theoretic terms Definitions and algorithms for: Dominators Back edges Natural loops 13

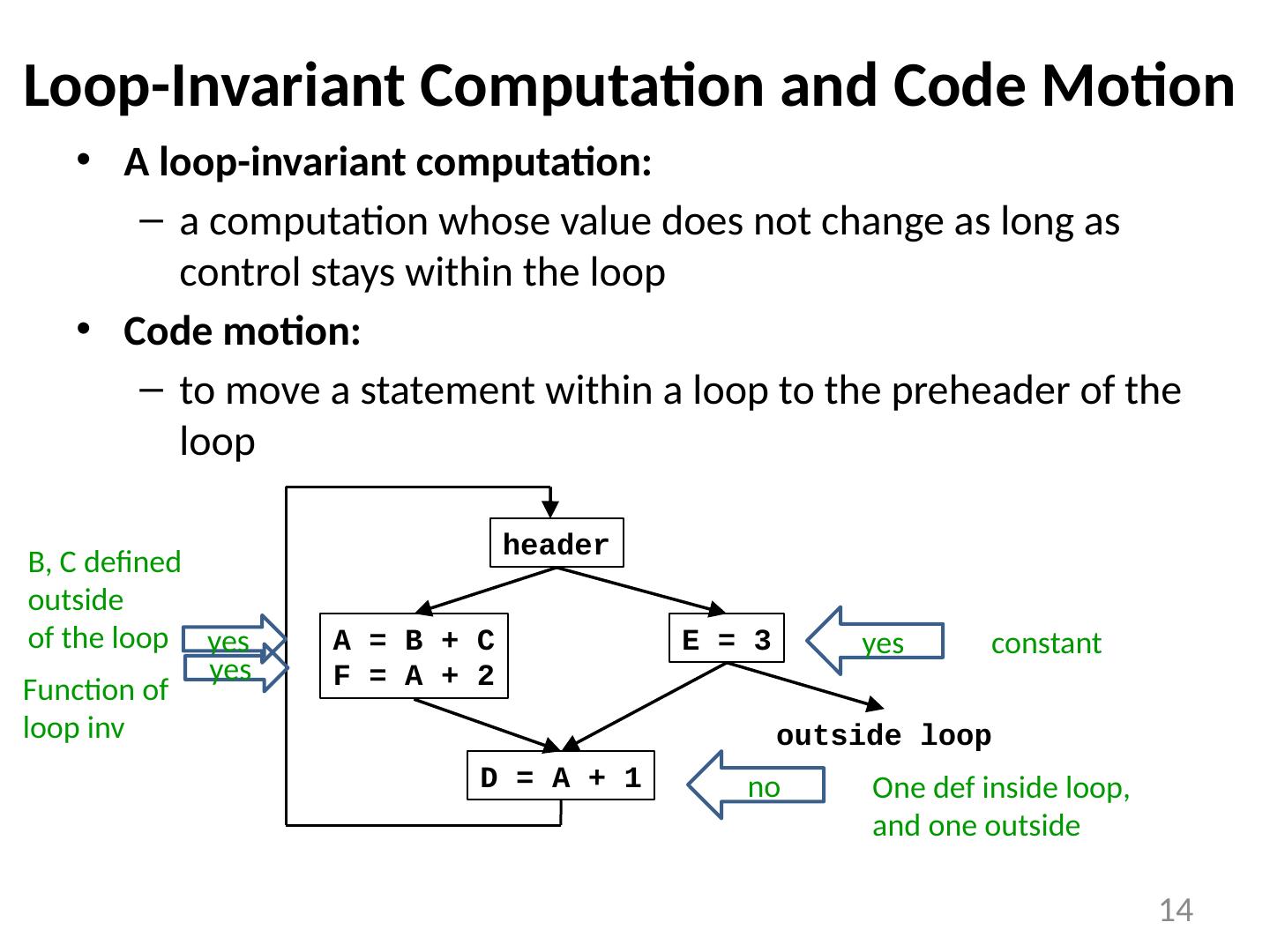
14 .Loop-Invariant Computation and Code Motion A loop-invariant computation: a computation whose value does not change as long as control stays within the loop Code motion: to move a statement within a loop to the preheader of the loop 14 A = B + C F = A + 2 E = 3 D = A + 1 header outside loop yes B, C defined outside of the loop yes Function of loop inv yes constant no One def inside loop, and one outside

15 .Algorithm Observations Loop invariant operands are defined outside loop or invariant themselves Code motion not all loop invariant instructions can be moved to preheader Algorithm Find invariant expressions Conditions for code motion Code transformation 15

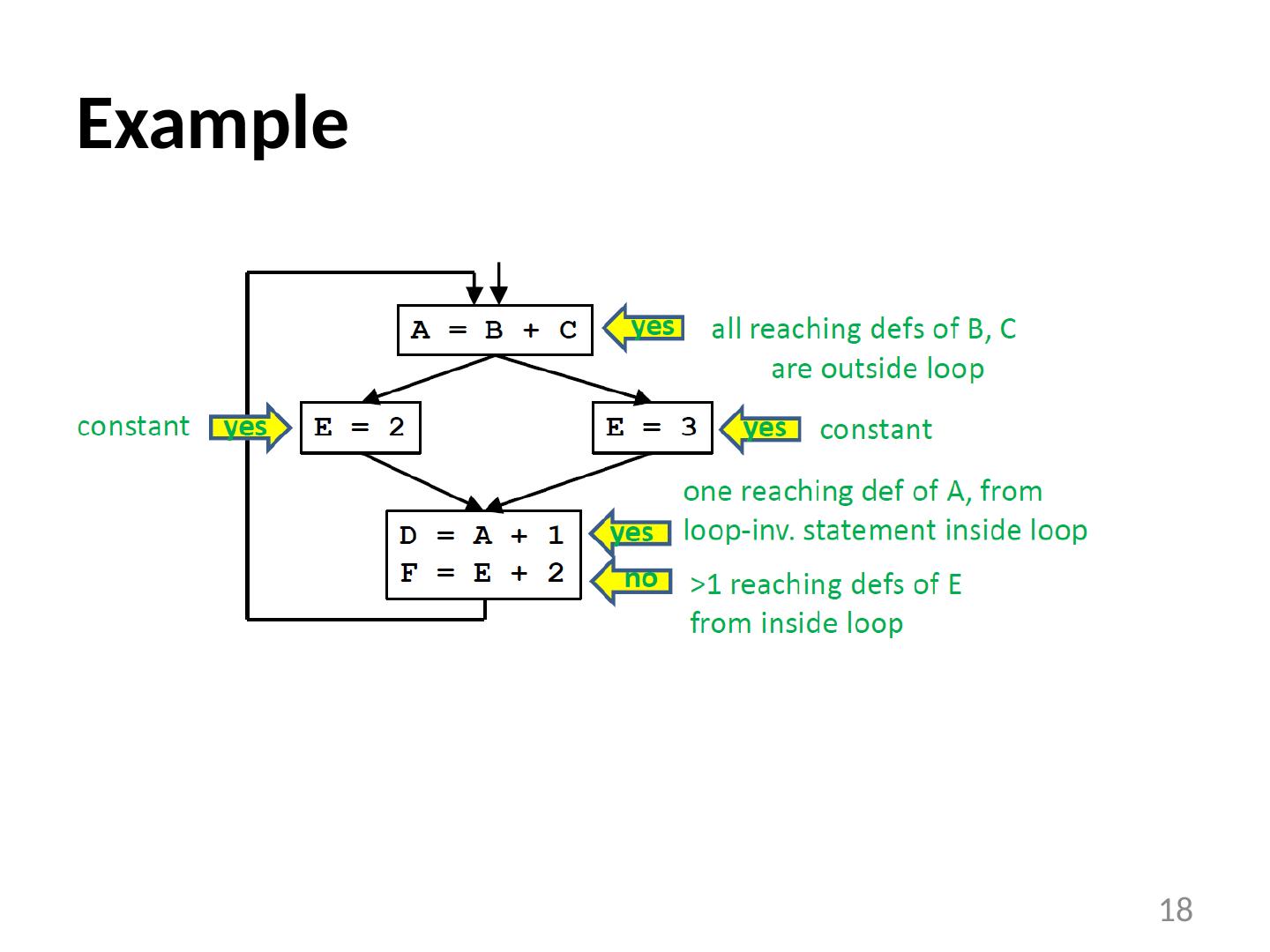
16 .Detecting Loop Invariant Computation Compute reaching definitions Mark INVARIANT if all the definitions of B and C that reach a statement A=B+C are outside the loop constant B, C? Repeat: Mark INVARIANT if all reaching definitions of B are outside the loop, or there is exactly one reaching definition for B, and it is from a loop-invariant statement inside the loop similarly for C until no changes to set of loop-invariant statements occur. 16

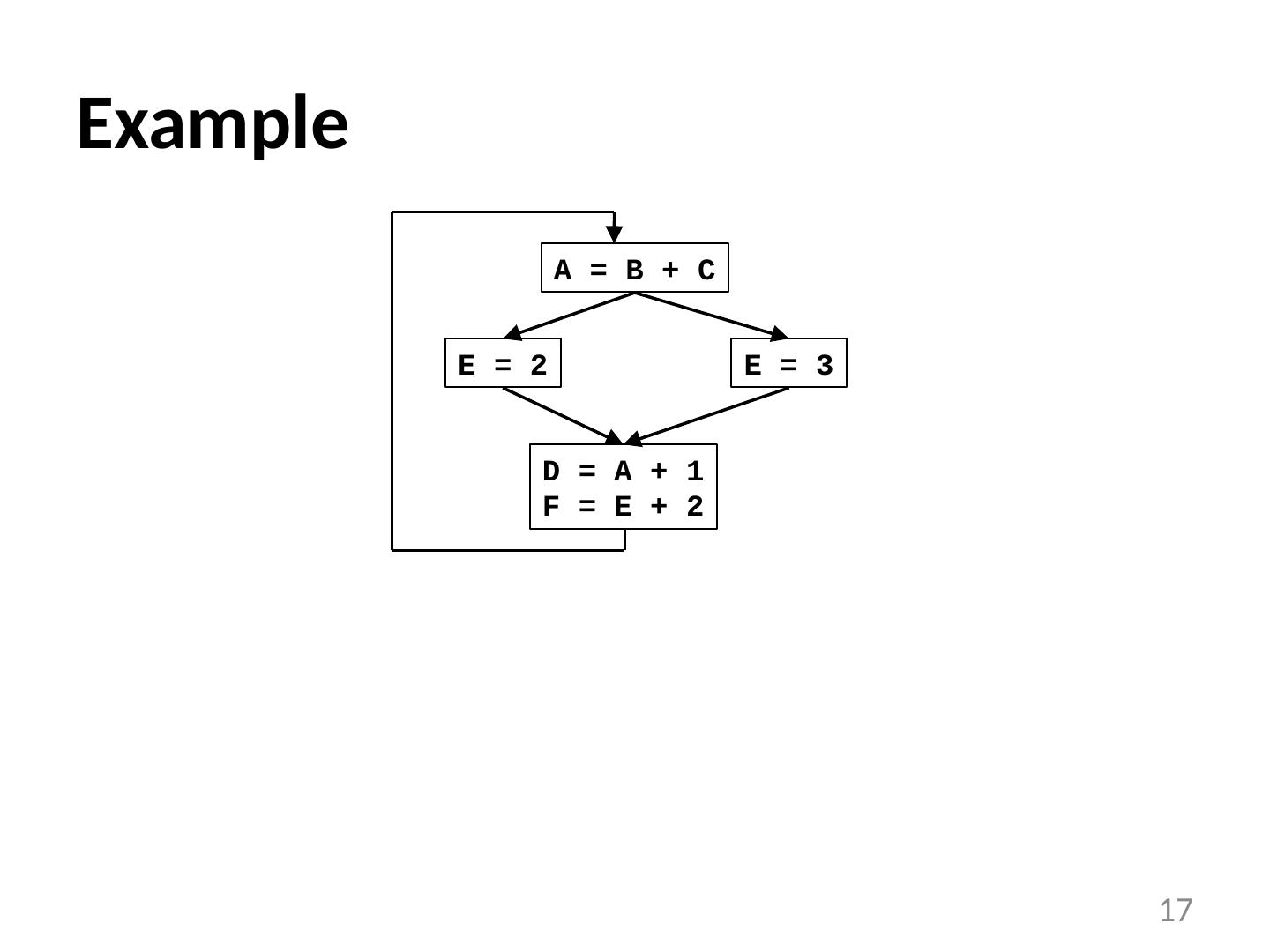
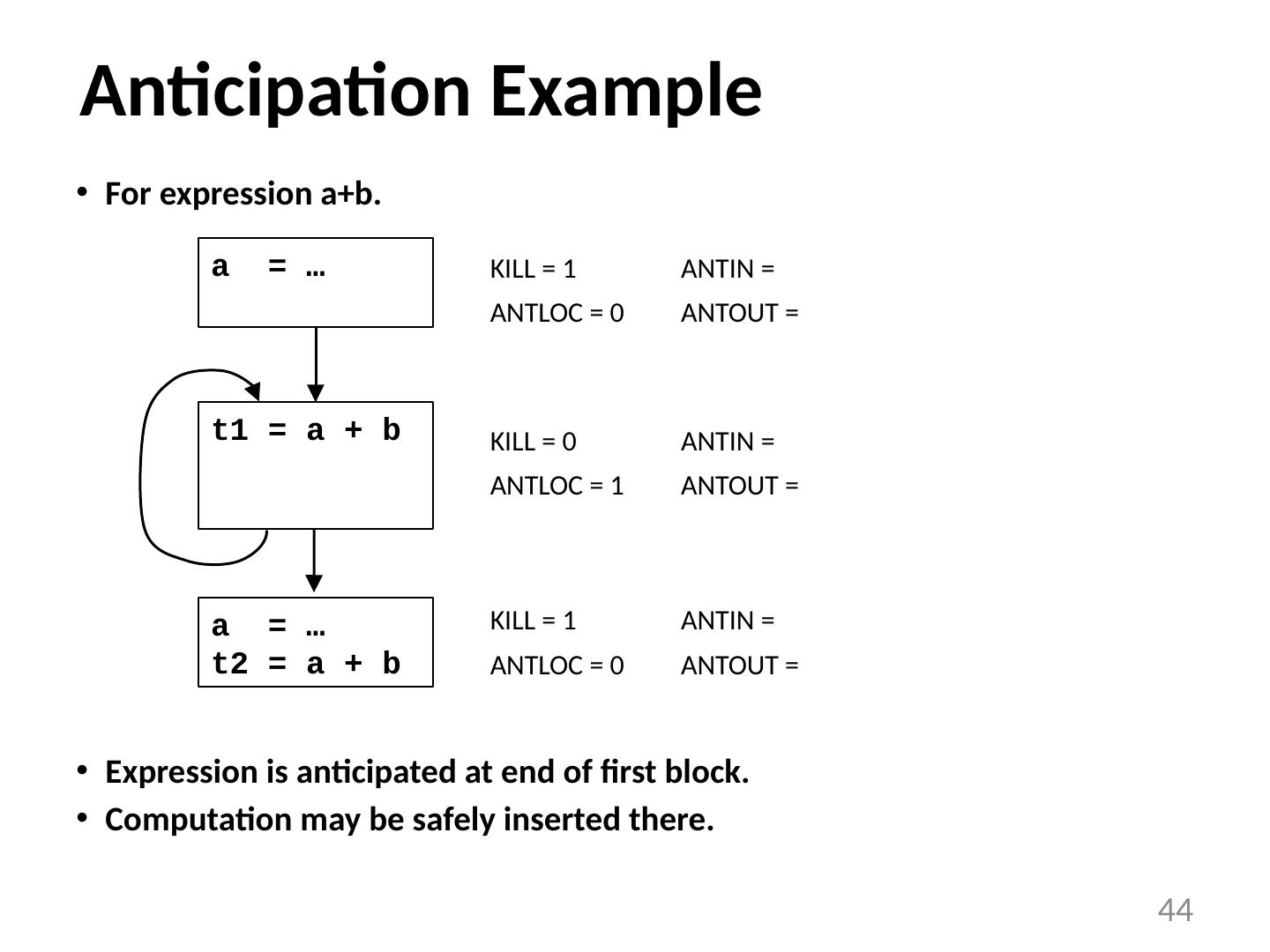
17 .Example 17 E = 2 E = 3 D = A + 1 F = E + 2 A = B + C

18 .Example 18

19 .Conditions for Code Motion Correctness : Movement does not change semantics of program Performance : Code is not slowed down Basic idea : defines once and for all control flow: once? Code dominates all exists other definitions: for all? No other definition other uses: for all? Dominates use or no other reaching defs to use 19

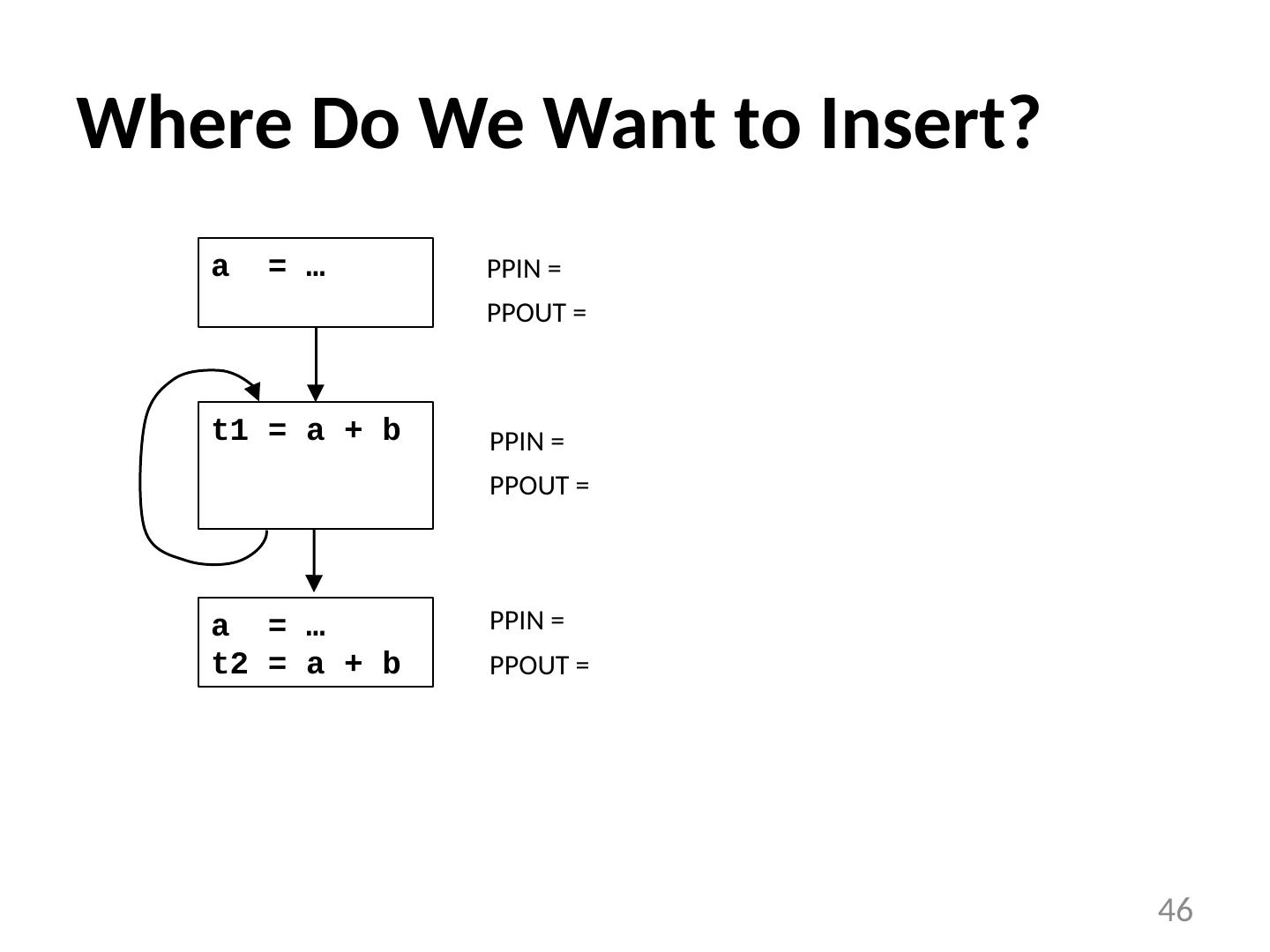
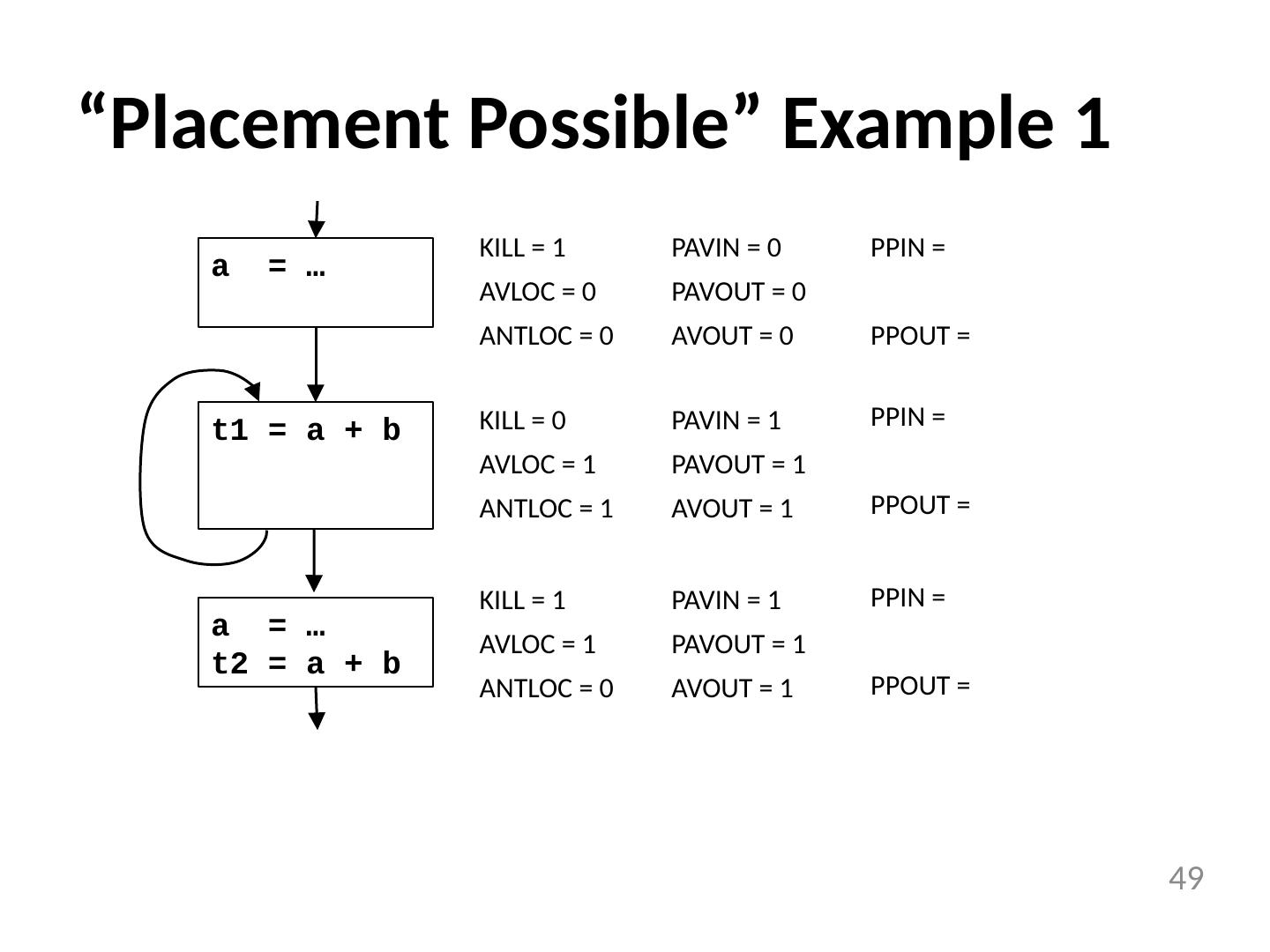
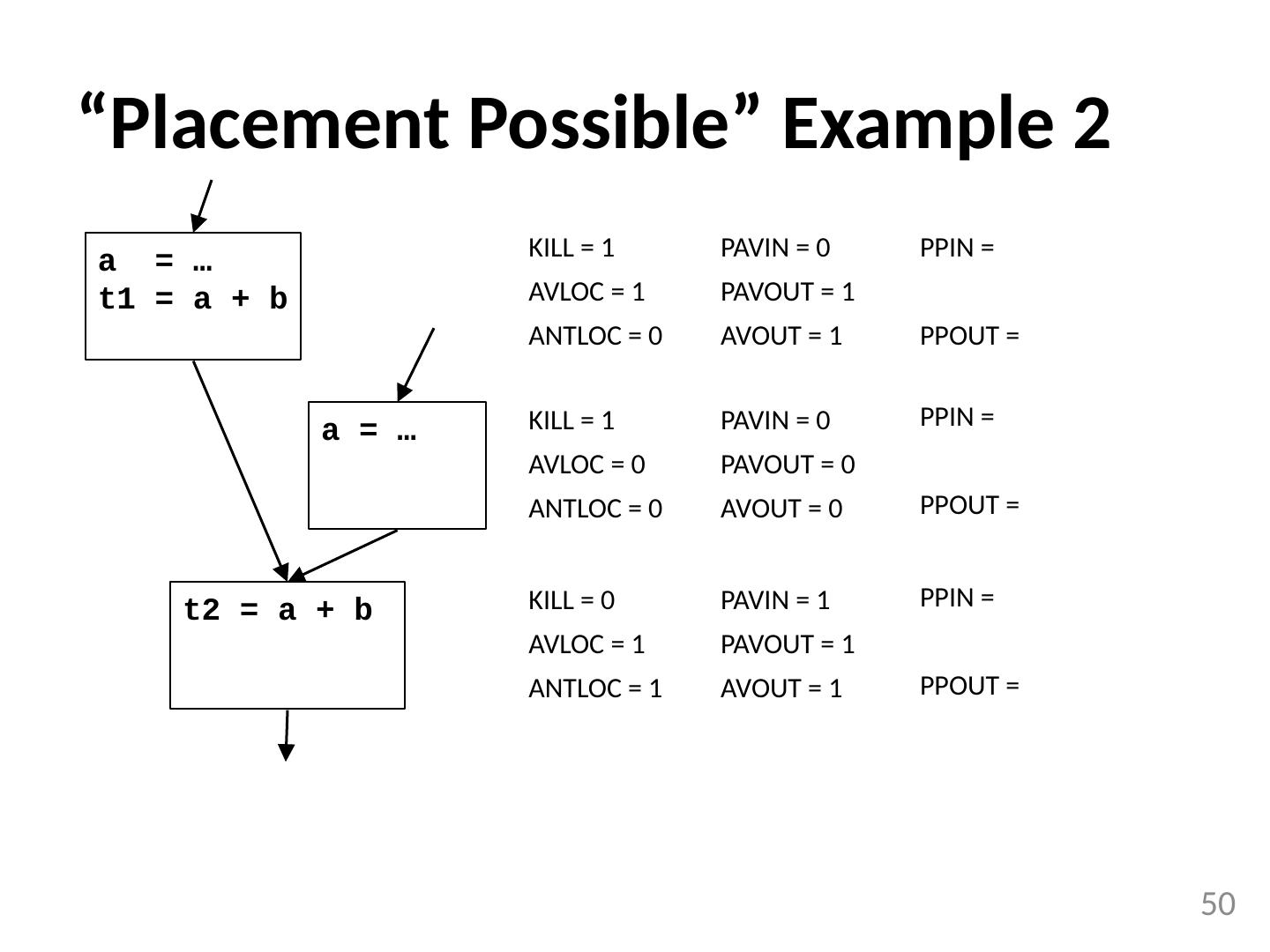
20 .Code Motion Algorithm Given: a set of nodes in a loop Compute reaching definitions Compute loop invariant computation Compute dominators Find the exits of the loop (i.e. nodes with successor outside loop) Candidate statement for code motion: loop invariant in blocks that dominate all the exits of the loop assign to variable not assigned to elsewhere in the loop in blocks that dominate all blocks in the loop that use the variable assigned Perform a depth-first search of the blocks Move candidate to preheader if all the invariant operations it depends upon have been moved 20

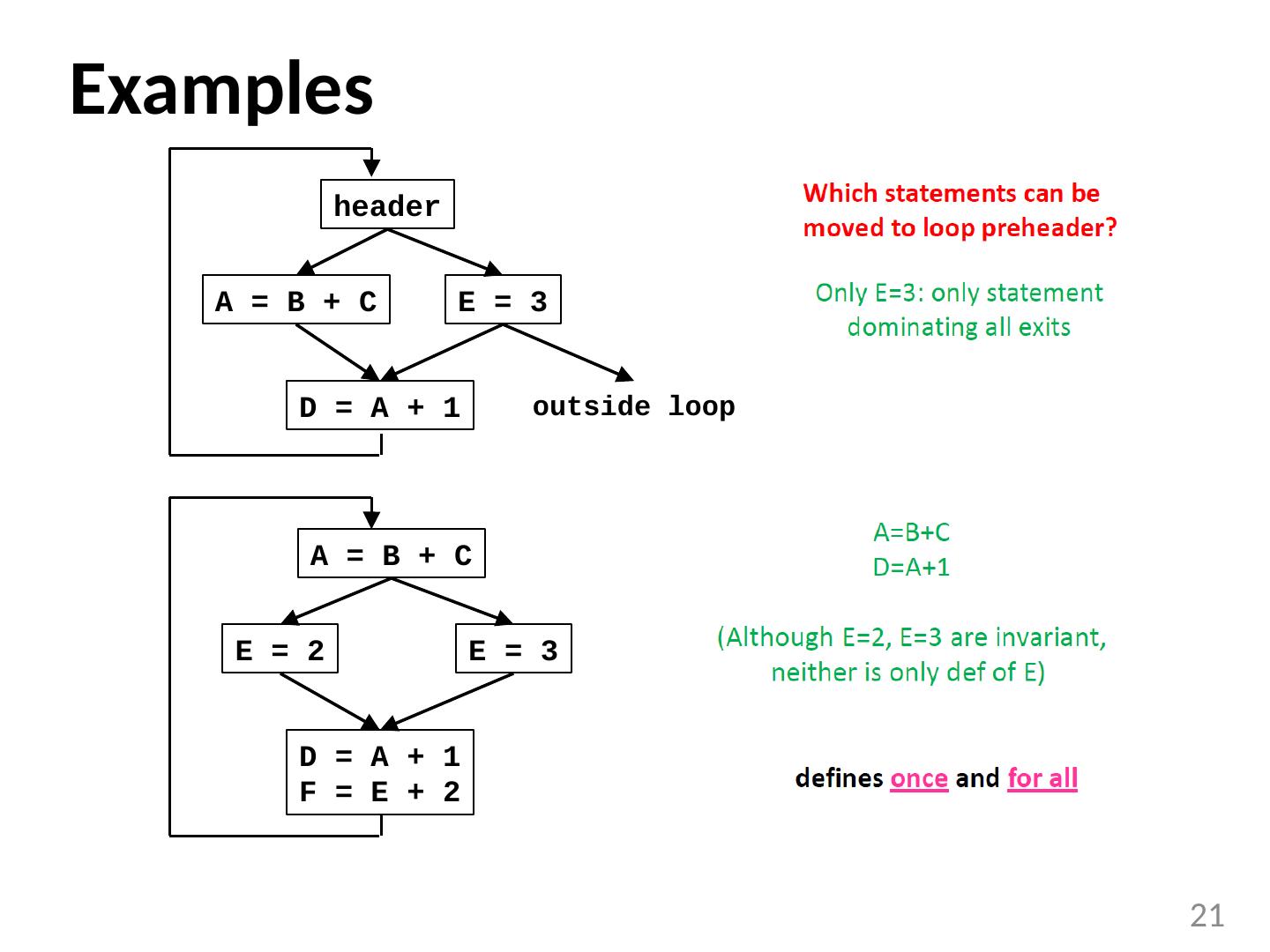
21 .Examples 21 E = 2 E = 3 D = A + 1 F = E + 2 A = B + C A = B + C E = 3 D = A + 1 header outside loop

22 .More Aggressive Optimizations Gamble on: most loops get executed Can we relax constraint of dominating all exits? Landing pads While p do s  if p { preheader repeat s until not p; } 22 A = B + C E = A + D D = … exit

23 .LICM Summary Precise definition and algorithm for loop invariant computation Precise algorithm for code motion Use of reaching definitions and dominators in optimizations 23

24 .Induction Variables and Strength Reduction Overview of optimization Algorithm to find induction variables 24

25 .Example FOR i = 0 to 100 A[ i ] = 0; i = 0 L2: IF i >=100 GOTO L1 t1 = 4 * i t2 = &A + t1 *t2 = 0 i = i+1 GOTO L2 L1: 25

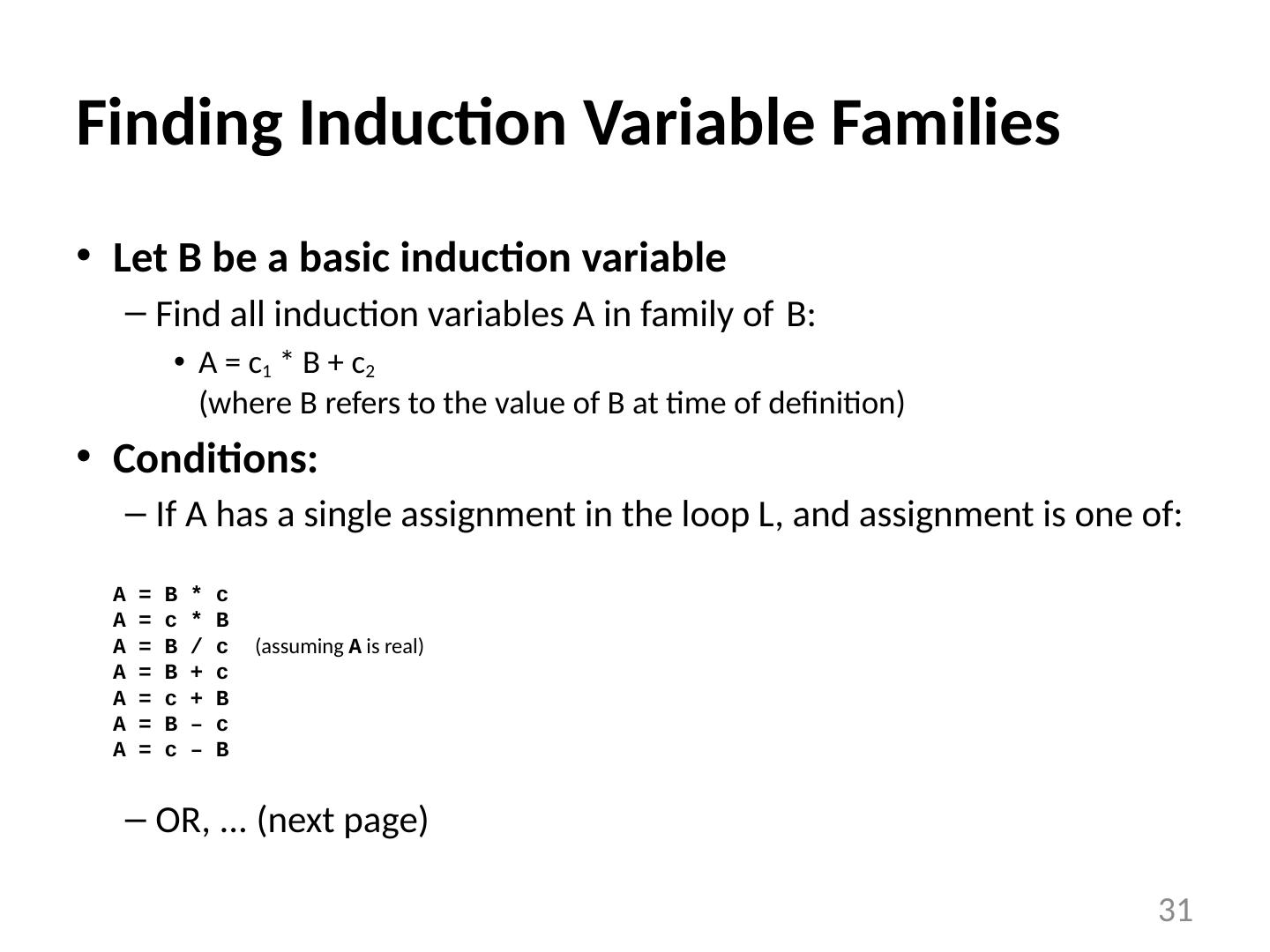
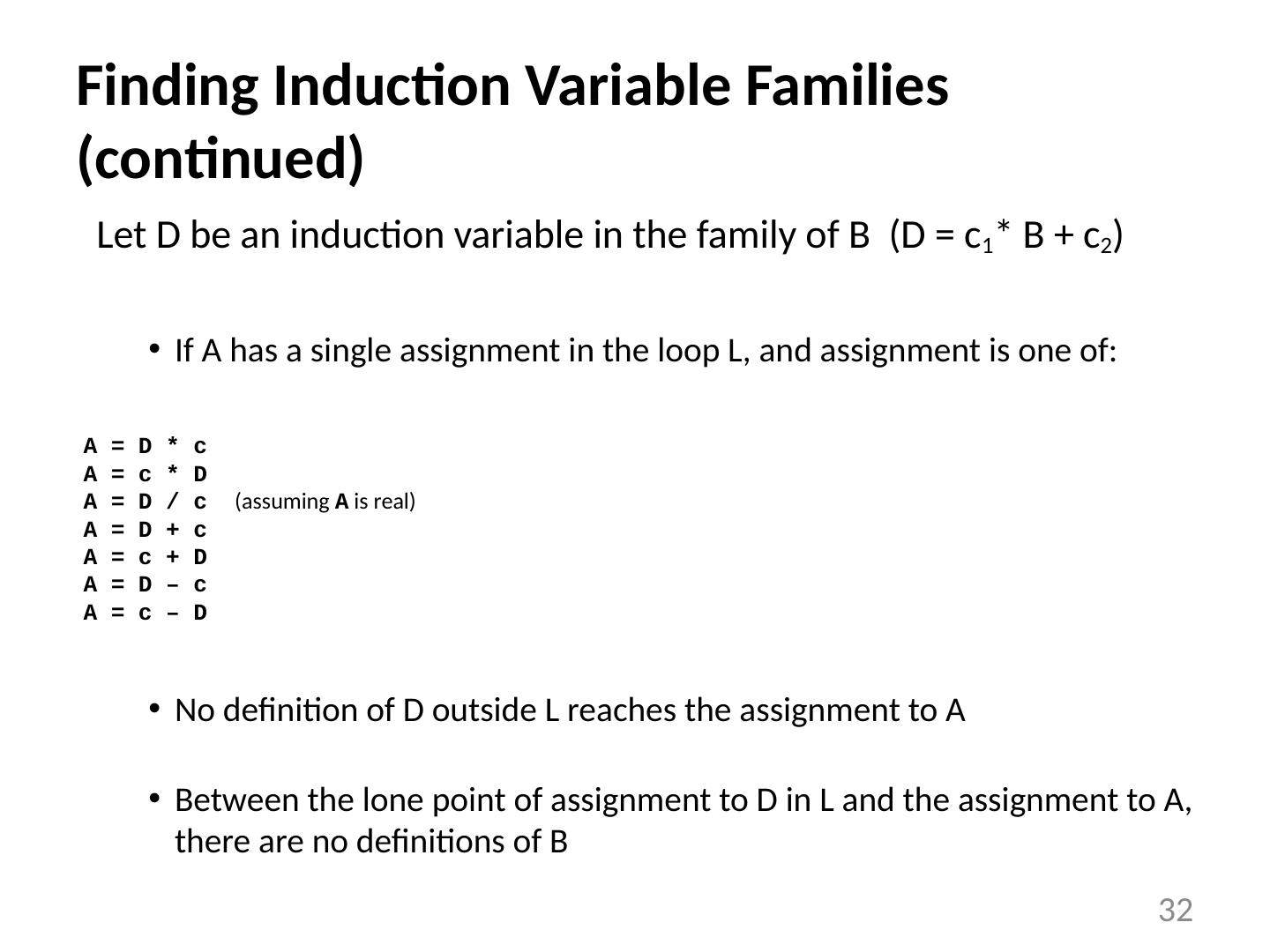
26 .Definitions A basic induction variable is a variable X whose only definitions within the loop are assignments of the form: X = X +c or X = X -c , where c is either a constant or a loop-invariant variable. An induction variable is a basic induction variable , or a variable defined once within the loop, whose value is a linear function of some basic induction variable at the time of the definition: A = c 1 * B + c 2 The FAMILY of a basic induction variable B is the set of induction variables A such that each time A is assigned in the loop, the value of A is a linear function of B. 26

27 .Optimizations Strength reduction: A is an induction variable in family of basic induction variable B ( A = c 1 * B + c 2 ) Create new variable : A’ Initialization in preheader : A’= c 1 * B + c 2 ; Track value of B: add after B= B+x : A’= A’+x *c 1 ; Replace assignment to A: A=A’ 27

28 .2. Optimizing non-basic induction variables copy propagation dead code elimination 3. Optimizing basic induction variables Eliminate basic induction variables used only for calculating other induction variables and loop tests Algorithm : Select an induction variable A in the family of B , preferably with simple constants (A = c 1 * B + c 2 ). Replace a comparison such as if B > X goto L1 with if ( A’ > c 1 * X + c 2 ) goto L1 (assuming c 1 is positive) if B is live at any exit from the loop, recompute it from A’ After the exit, B = (A’ - c 2 ) / c 1 Optimizations (continued) 28

29 .II. Basic Induction Variables A BASIC induction variable in a loop L a variable X whose only definitions within L are assignments of the form: X = X+c or X = X-c , where c is either a constant or a loop-invariant variable. Algorithm : can be detected by scanning L Example : k = 0; for (i = 0; i < n; i++) { k = k + 3; … = m; if (x < y) k = k + 4; if (a < b) m = 2 * k; k = k – 2; … = m; Each iteration may execute a different number of increments/decrements!! 29