Lecture 4 [SSA]

1 .CSC D70: Compiler Optimization Static Single Assignment (SSA) Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Phillip Gibbons

2 .From Last Lecture What is a Loop? Dominator Tree Natural Loops Back Edges 2

3 .Finding Loops: Summary Define loops in graph theoretic terms Definitions and algorithms for: Dominators Back edges Natural loops 3

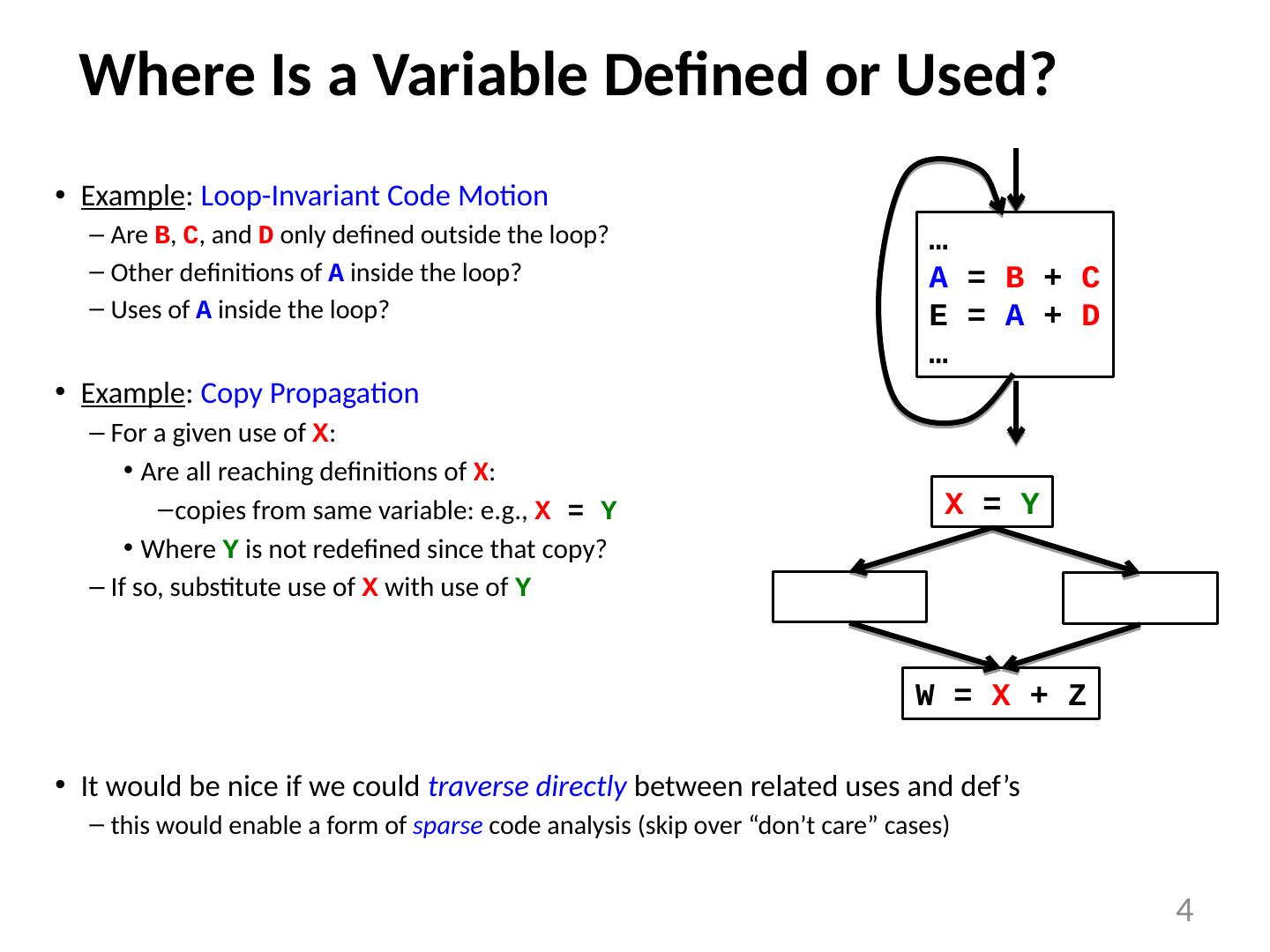
4 .Where Is a Variable Defined or Used? Example : Loop-Invariant Code Motion Are B , C , and D only defined outside the loop? Other definitions of A inside the loop? Uses of A inside the loop? Example : Copy Propagation For a given use of X : Are all reaching definitions of X : copies from same variable: e.g., X = Y Where Y is not redefined since that copy? If so, substitute use of X with use of Y It would be nice if we could traverse directly between related uses and def’s this would enable a form of sparse code analysis (skip over “don’t care” cases) 4 … A = B + C E = A + D … X = Y W = X + Z X = Y X = Y

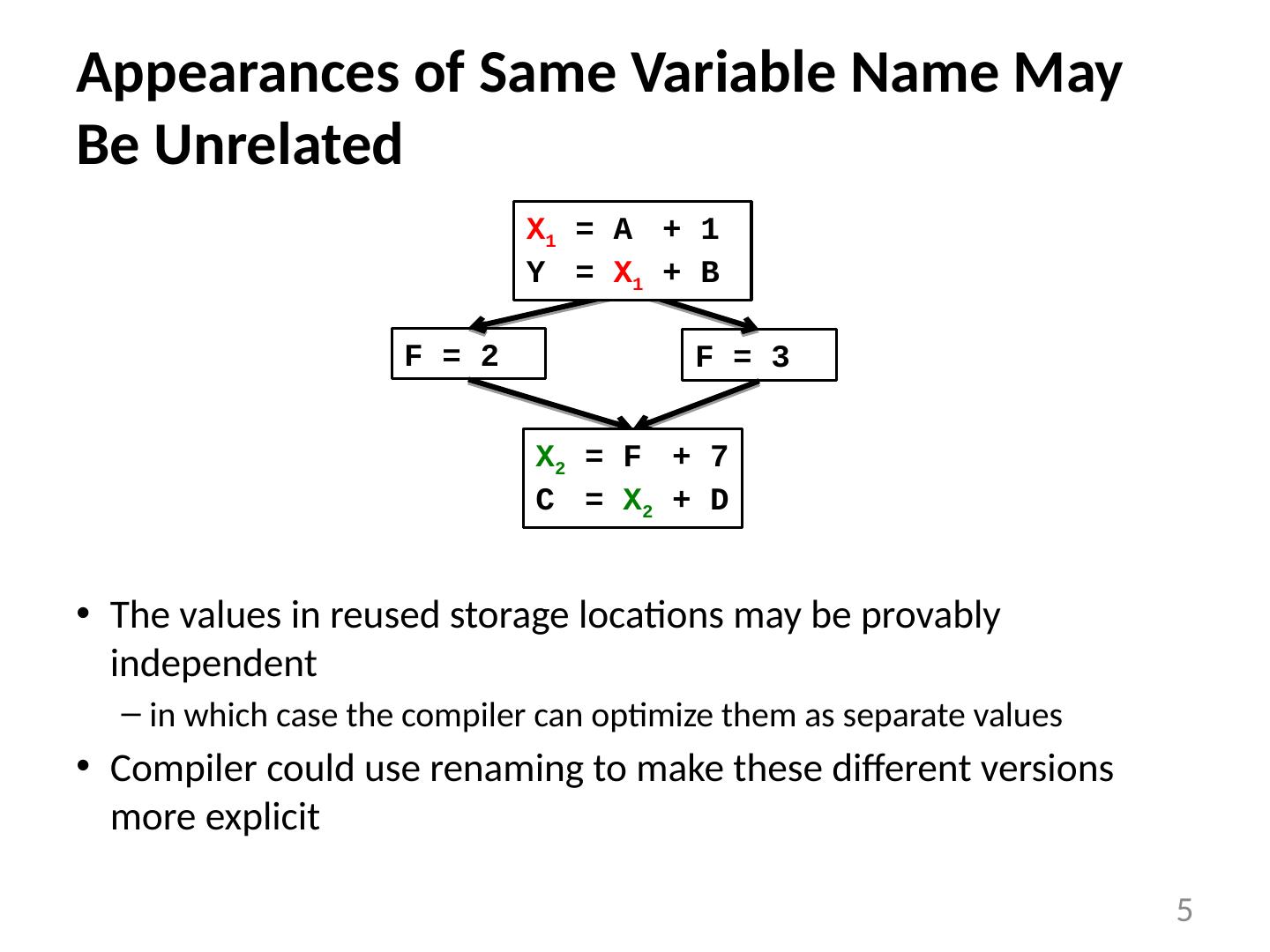
5 .Appearances of Same Variable Name May Be Unrelated The values in reused storage locations may be provably independent in which case the compiler can optimize them as separate values Compiler could use renaming to make these different versions more explicit 5 X 1 = A 2 + 1 Y 2 = X 1 + B X 2 = F 2 + 7 C 2 = X 2 + D F = 3 F = 2 X 1 = A 2 + 1 Y 2 = X 1 + B X 2 = F 2 + 7 C 2 = X 2 + D

6 .Definition-Use and Use-Definition Chains Use-Definition (UD) Chains: for a given definition of a variable X, what are all of its uses? Definition-Use (DU) Chains: for a given use of a variable X, what are all of the reaching definitions of X? 6 X 1 = A 2 + 1 Y 2 = X 1 + B X 2 = F 2 + 7 C 2 = X 2 + D F = 3 F = 2 X 1 = A 2 + 1 Y 2 = X 1 + B X 2 = F 2 + 7 C 2 = X 2 + D

7 .7 DU and UD Chains Can Be Expensive foo ( int i , int j) { … switch ( i ) { case 0: x=3;break; case 1: x=1; break; case 2: x =6; break; case 3: x=7; break; default: x = 11; } switch (j) { case 0: y= x +7; break; case 1: y=x+4; break; case 2: y=x-2; break; case 3: y=x+1; break; default: y=x+9; } … In general, N defs M uses  O(NM) space and time One solution : limit each variable to ONE definition site

8 .8 DU and UD Chains Can Be Expensive (2) foo ( int i , int j) { … switch ( i ) { case 0: x=3; break; case 1: x=1; break; case 2: x=6; case 3: x=7; default: x = 11; } x1 is one of the above x’s switch (j) { case 0: y=x 1 +7; case 1: y=x 1 +4; case 2: y=x 1 -2; case 3: y=x 1 +1; default: y=x 1 +9; } … One solution : limit each variable to ONE definition site

9 .9 Static Single Assignment (SSA) Static single assignment is an IR where every variable is assigned a value at most once in the program text Easy for a basic block (reminiscent of Value Numbering): Visit each instruction in program order: LHS: assign to a fresh version of the variable RHS : use the most recent version of each variable a  x + y b  a + x a  b + 2 c  y + 1 a  c + a a 1  x + y b 1  a 1 + x a 2  b 1 + 2 c 1  y + 1 a 3  c 1 + a 2

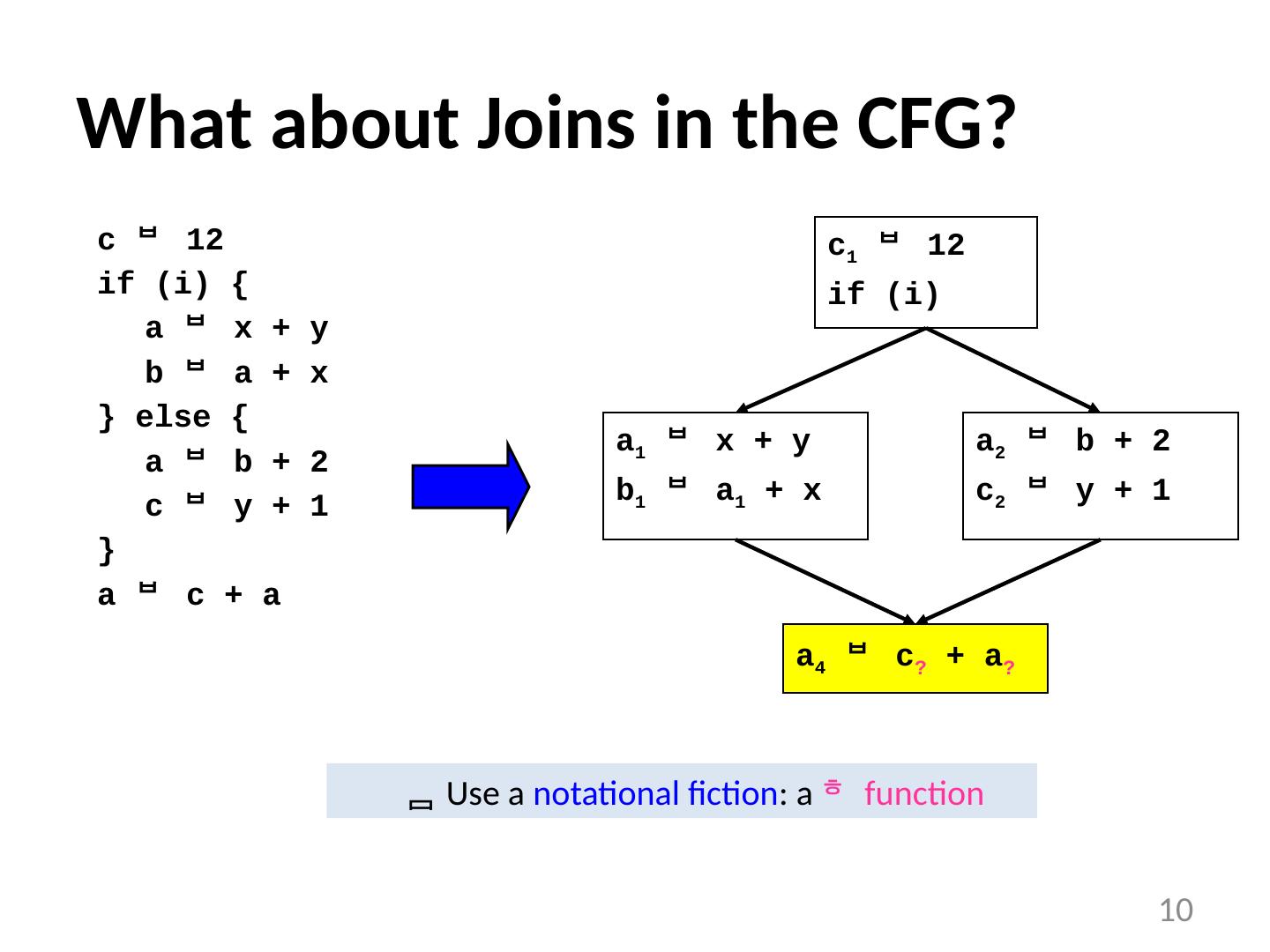
10 .10 a 1  x + y b 1  a 1 + x What about Joins in the CFG? a 2  b + 2 c 2  y + 1 c  12 if (i) { a  x + y b  a + x } else { a  b + 2 c  y + 1 } a  c + a c 1  12 if ( i ) a 4  c ? + a ?  Use a notational fiction : a  function

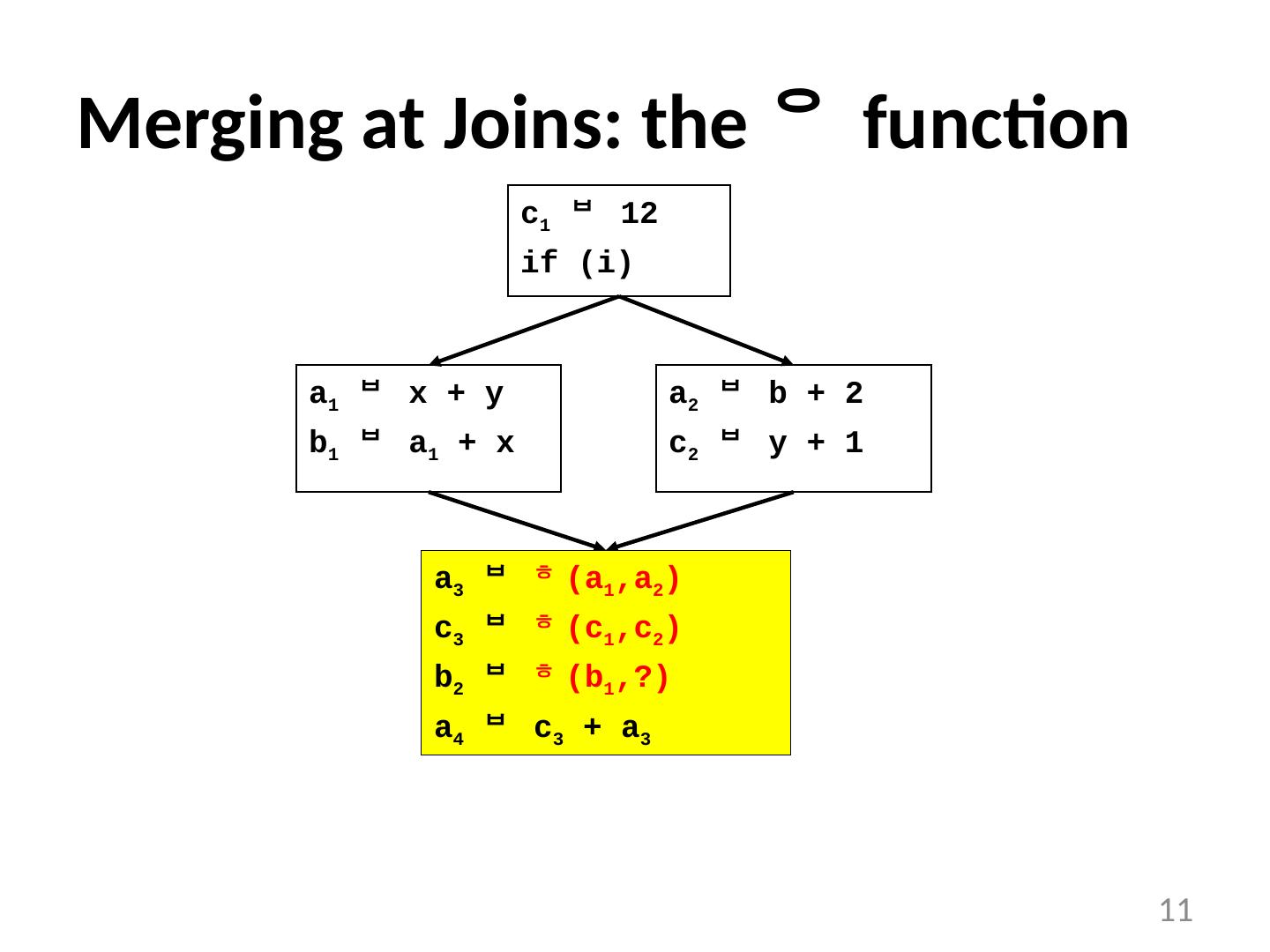
11 .Merging at Joins: the  function 11 a 1  x + y b 1  a 1 + x a 2  b + 2 c 2  y + 1 c 1  12 if ( i ) a 3   (a 1 ,a 2 ) c 3   (c 1 ,c 2 ) b 2   (b 1 ,?) a 4  c 3 + a 3

12 .12 The  function  merges multiple definitions along multiple control paths into a single definition . At a basic block with p predecessors, there are p arguments to the  function. x new   ( x 1 , x 1 , x 1 , … , x p ) How do we choose which x i to use? We don’t really care! If we care, use moves on each incoming edge

13 .13 “Implementing”  a 2  b + 2 c 2  y + 1 a 3  a 2 c 3  c 2 c 1  12 if ( i ) a 1  x + y b 1  a 1 + x a 3  a 1 c 3  c 1 a 3   (a 1 ,a 2 ) c 3   (c 1 ,c 2 ) a 4  c 3 + a 3

14 .14 Trivial SSA Each assignment generates a fresh variable. At each join point insert  functions for all live variables . y  x y  2 z  y + x x  1 y 1  x 1 y 2  2 x 2  (x 1 ,x 1 ) y 3  (y 1 ,y 2 ) z 1  y 3 + x 2 x 1  1 Too many  functions inserted.

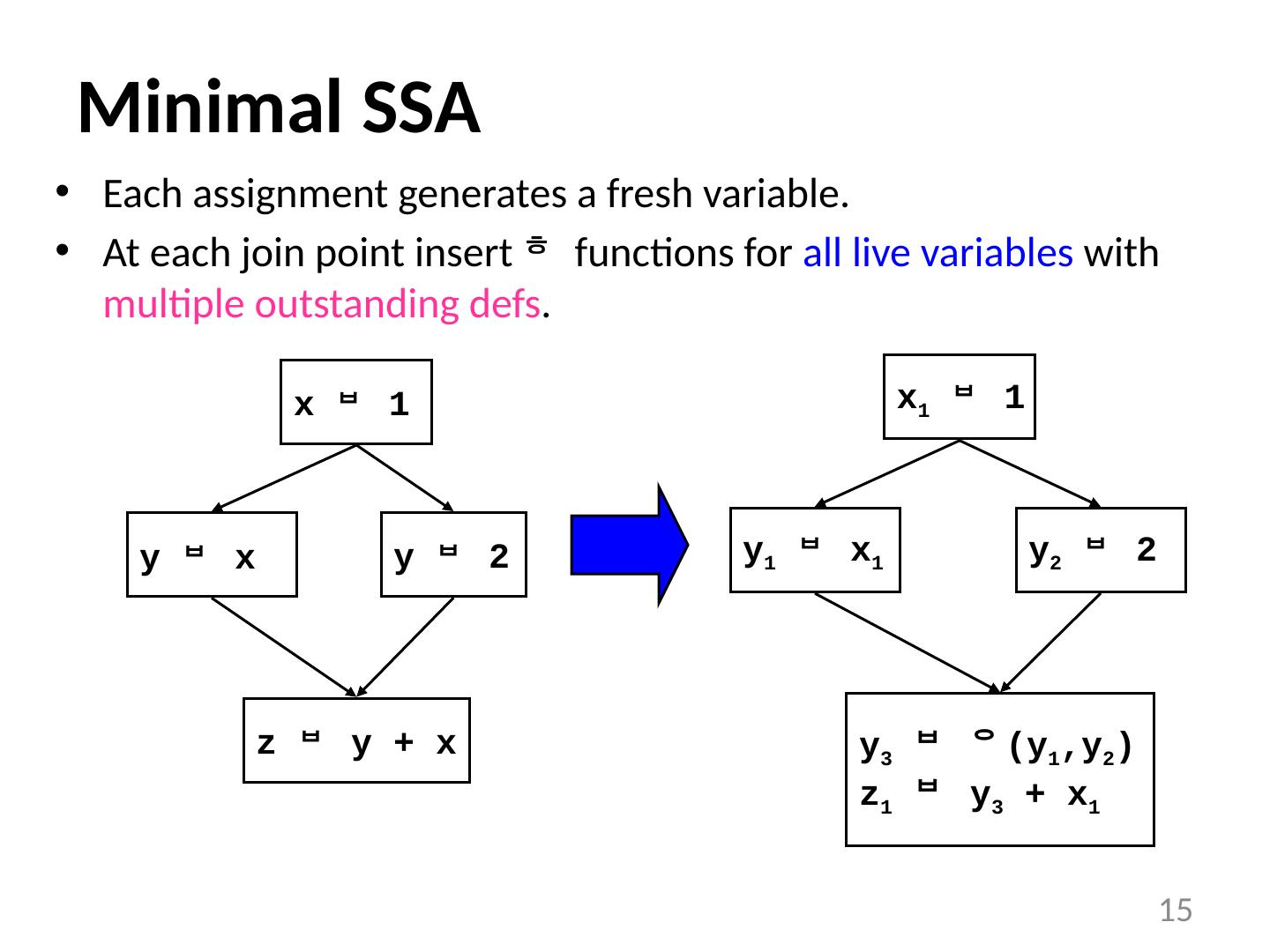
15 .15 Minimal SSA Each assignment generates a fresh variable. At each join point insert  functions for all live variables with multiple outstanding defs . y  x y  2 z  y + x x  1 y 1  x 1 y 2  2 y 3  (y 1 ,y 2 ) z 1  y 3 + x 1 x 1  1

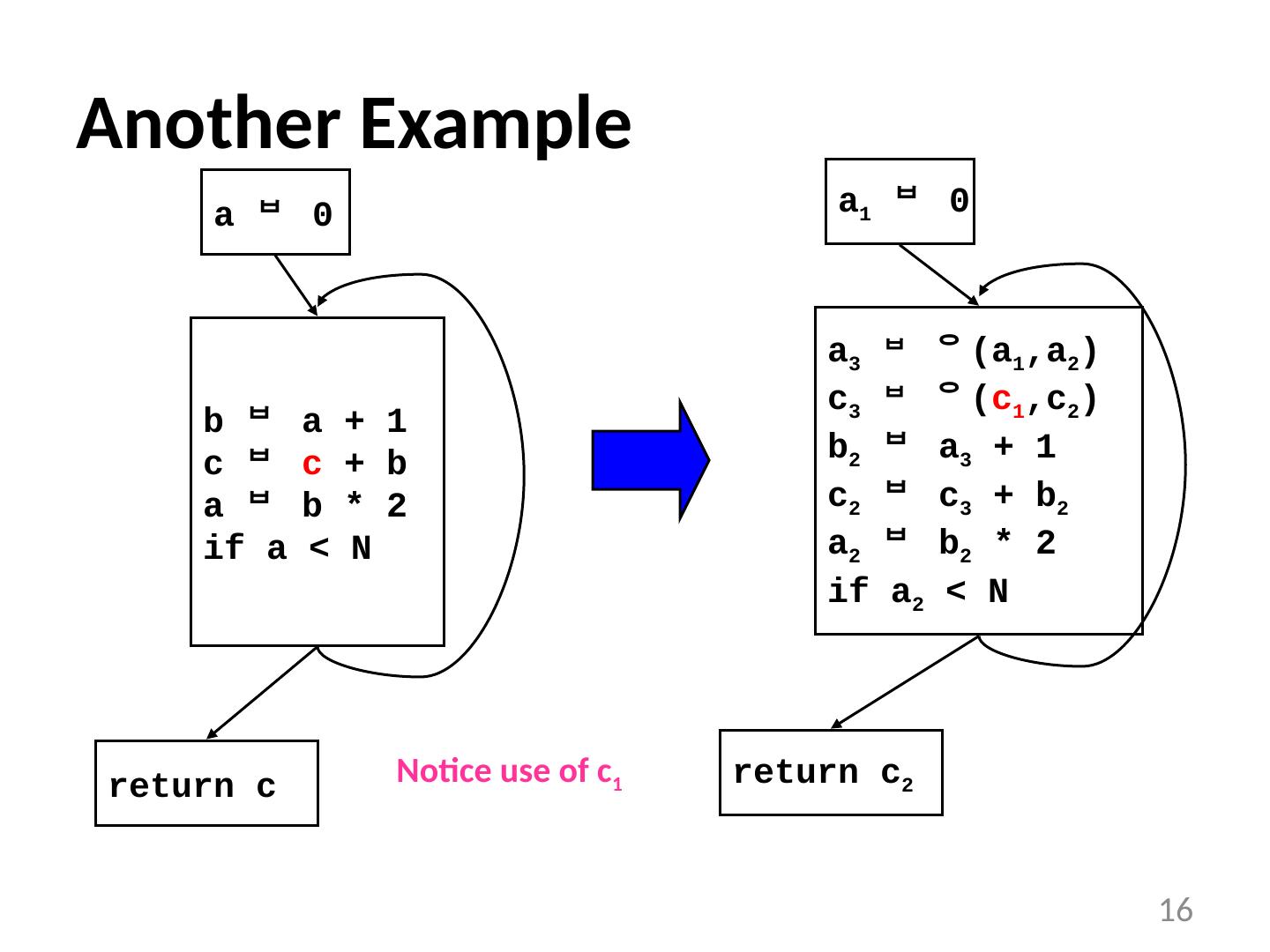
16 .16 Another Example a  0 b  a + 1 c  c + b a  b * 2 if a < N return c a 1  0 a 3  (a 1 ,a 2 ) c 3  ( c 1 ,c 2 ) b 2  a 3 + 1 c 2  c 3 + b 2 a 2  b 2 * 2 if a 2 < N return c 2 Notice use of c 1

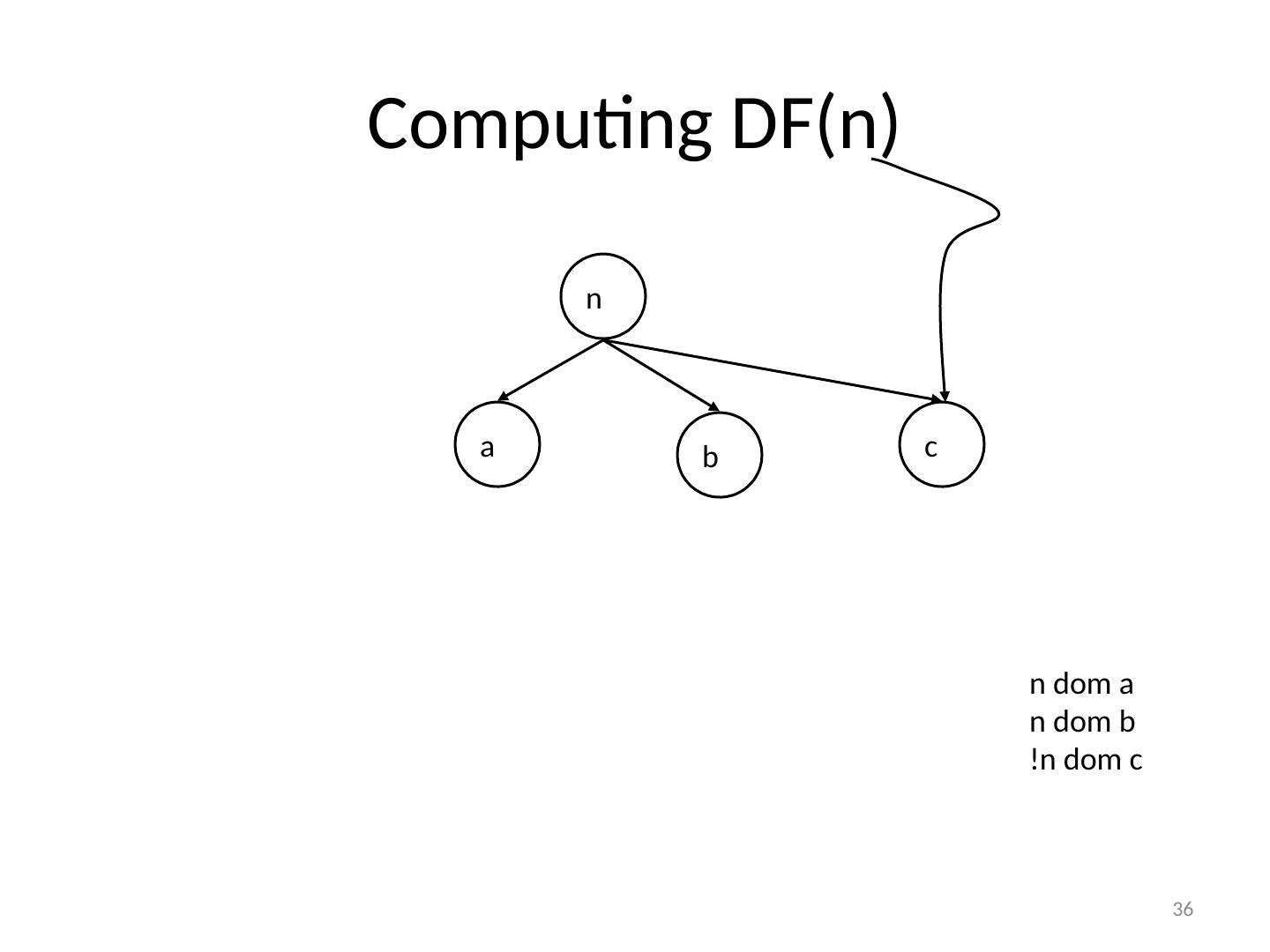
17 .17 When Do We Insert ? 11 1 5 6 7 8 13 2 3 4 9 10 12 CFG If there is a def of a in block 5 , which nodes need a ()?

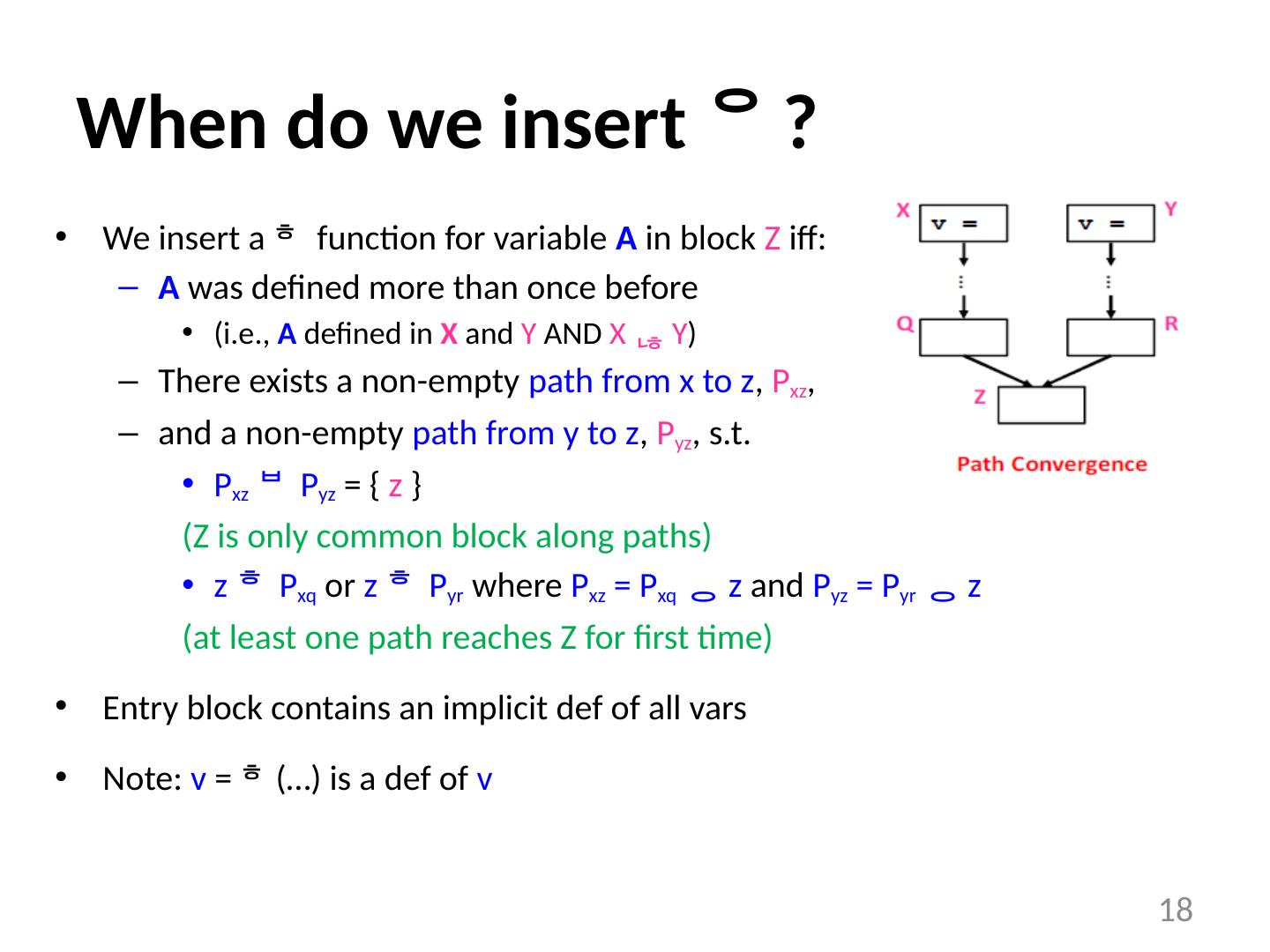
18 .18 When do we insert ? We insert a  function for variable A in block Z iff : A was defined more than once before (i.e., A defined in X and Y AND X  Y ) There exists a non-empty path from x to z , P xz , and a non-empty path from y to z , P yz , s.t. P xz  P yz = { z } (Z is only common block along paths) z  P xq or z  P yr where P xz = P xq  z and P yz = P yr  z (at least one path reaches Z for first time) Entry block contains an implicit def of all vars Note: v = (…) is a def of v

19 .19 Dominance Property of SSA In SSA, definitions dominate uses . If x i is used in x  (…, x i , …) , then BB(x i ) dominates i th predecessor of BB(PHI) If x is used in y  … x … , then BB(x) dominates BB(y) We can use this for an efficient algorithm to convert to SSA

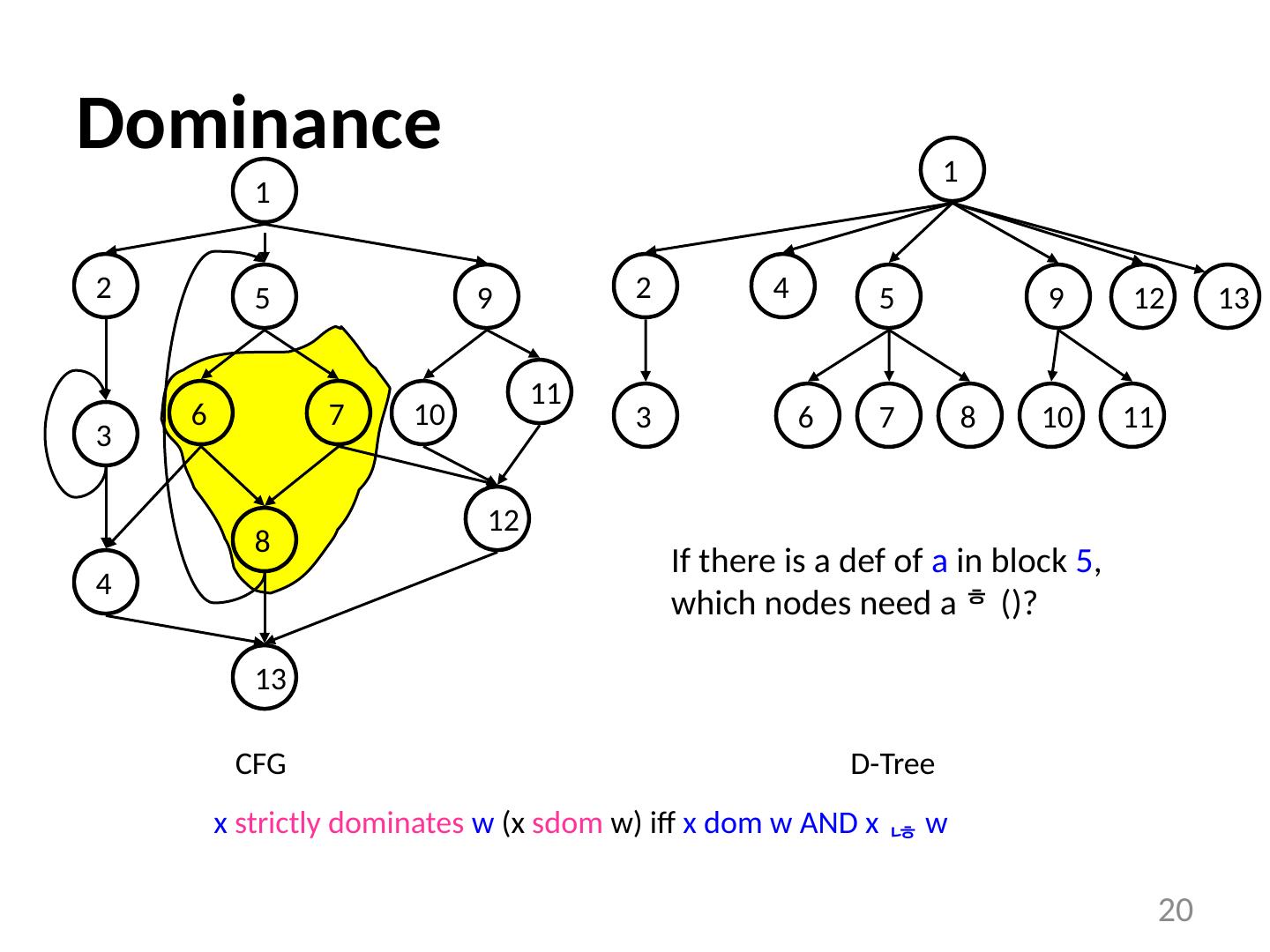
20 .20 Dominance 11 1 5 6 7 8 13 2 3 4 9 10 12 1 11 5 6 7 8 2 3 4 9 10 12 13 CFG D-Tree x strictly dominates w (x sdom w) iff x dom w AND x  w If there is a def of a in block 5 , which nodes need a ()?

21 .21 Dominance Frontier 11 1 5 6 7 8 13 2 3 4 9 10 12 CFG D-Tree The Dominance Frontier of a node x = { w | x dom pred (w) AND !(x sdom w)} 1 11 5 6 7 8 2 3 4 9 10 12 13 x strictly dominates w (x sdom w) iff x dom w AND x  w

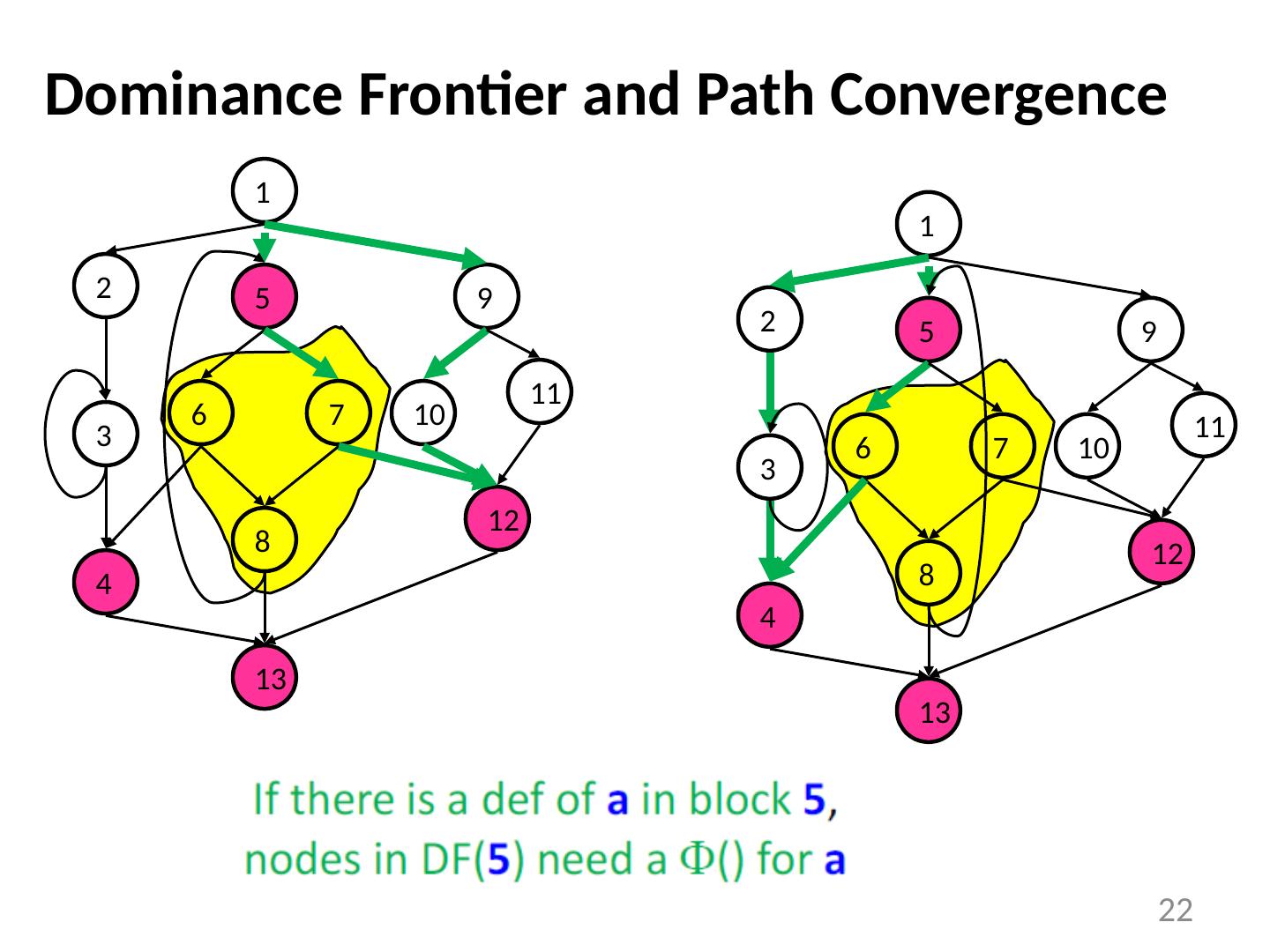
22 .22 Dominance Frontier and Path Convergence 11 1 5 6 7 8 13 2 3 4 9 10 12 11 1 5 6 7 8 13 2 3 4 9 10 12

23 .Using Dominance Frontier to Compute SSA place all () Rename all variables 23

24 .24 Using Dominance Frontier to Place () Gather all the defsites of every variable Then, for every variable foreach defsite foreach node in DominanceFrontier ( defsite ) if we haven’t put () in node, then put one in if this node didn’t define the variable before, then add this node to the defsites This essentially computes the Iterated Dominance Frontier on the fly, inserting the minimal number of () neccesary

25 .25 Using Dominance Frontier to Place () foreach node n { foreach variable v defined in n { orig [n]  = {v} defsites [v]  = {n} } } foreach variable v { W = defsites [v] while W not empty { n = remove node from W foreach y in DF[n] if y  PHI[v] { insert “v  ( v,v ,…)” at top of y PHI[v] = PHI[v]  {y} if v  orig [y]: W = W  {y} } } }

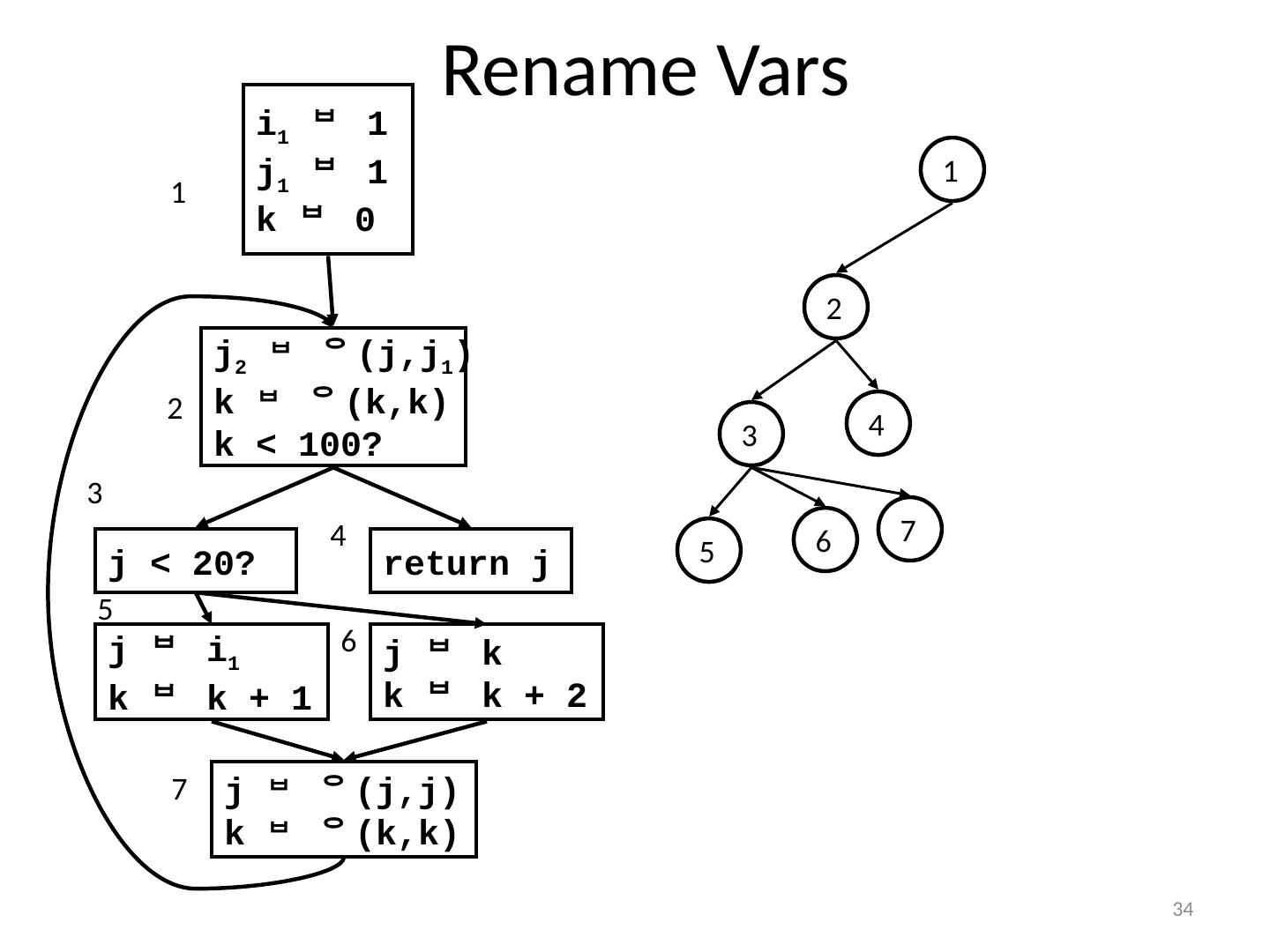
26 .26 Renaming Variables Algorithm : Walk the D-tree, renaming variables as you go Replace uses with more recent renamed def For straight-line code this is easy What if there are branches and joins? use the closest def such that the def is above the use in the D-tree Easy implementation: for each var : rename (v) rename (v): replace uses with top of stack at def: push onto stack call rename(v) on all children in D-tree for each def in this block pop from stack

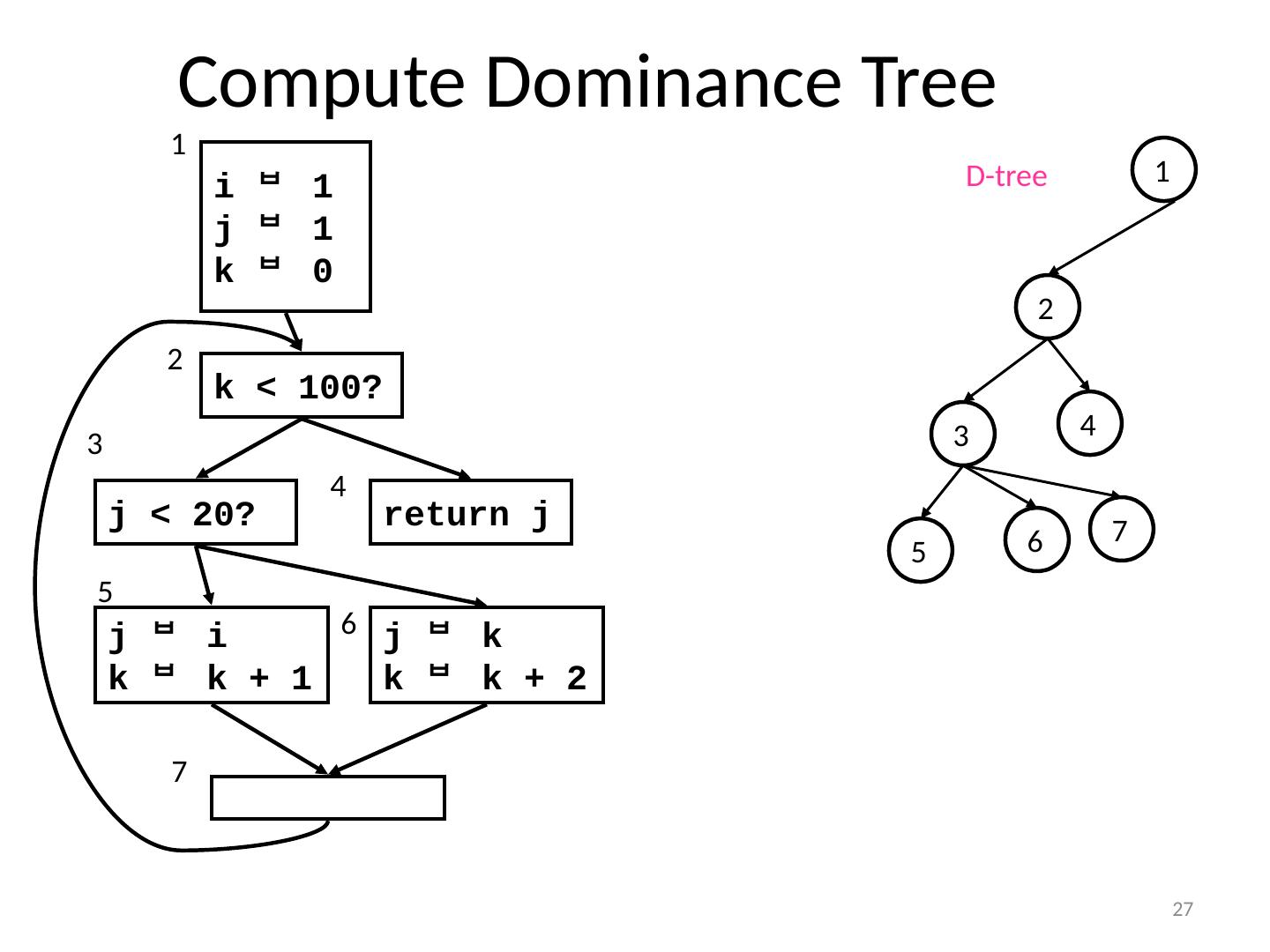
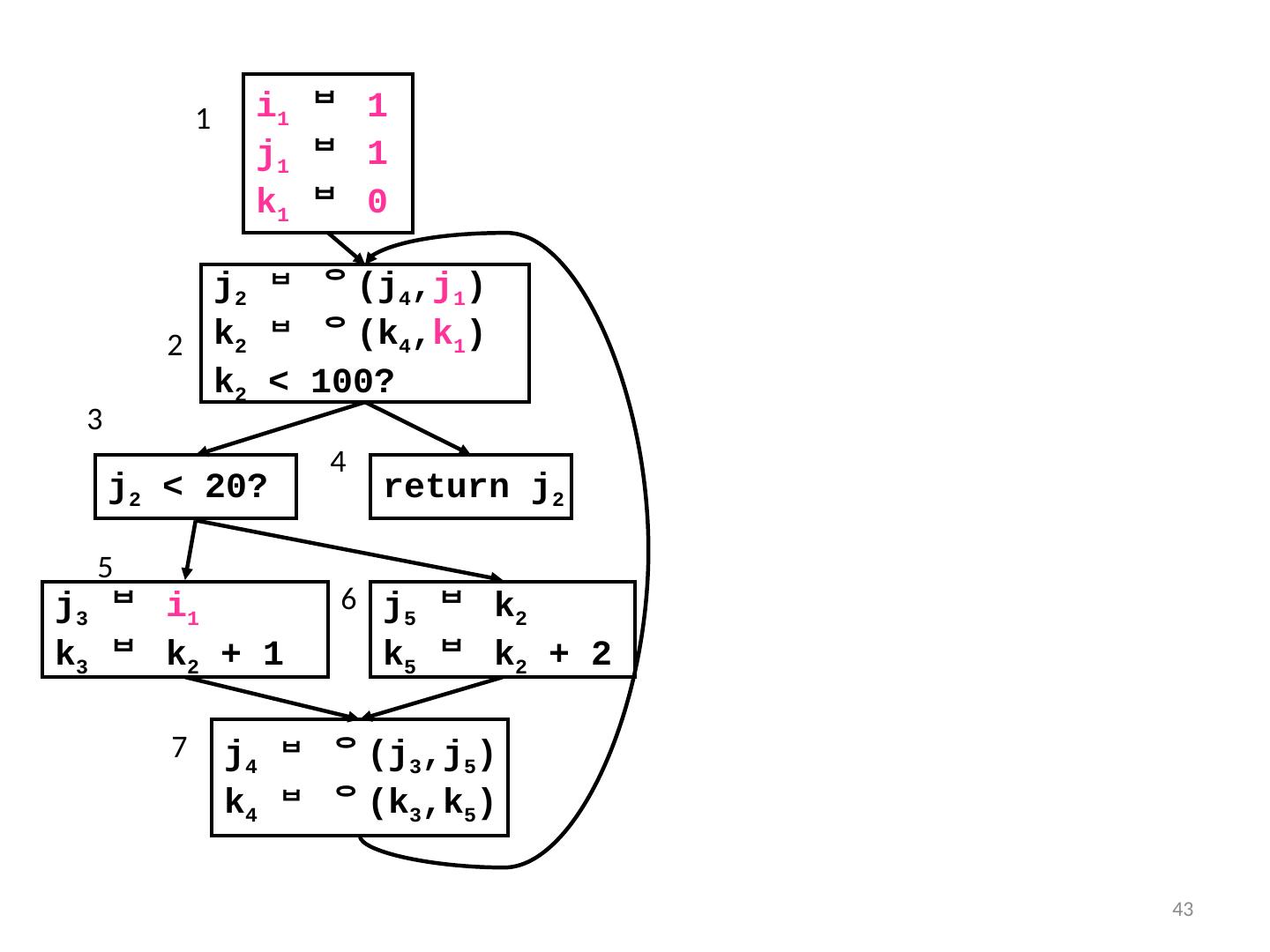
27 .27 Compute Dominance Tree i  1 j  1 k  0 k < 100? j < 20? return j j  i k  k + 1 j  k k  k + 2 1 2 4 6 5 7 1 5 6 7 3 4 2 3 D-tree

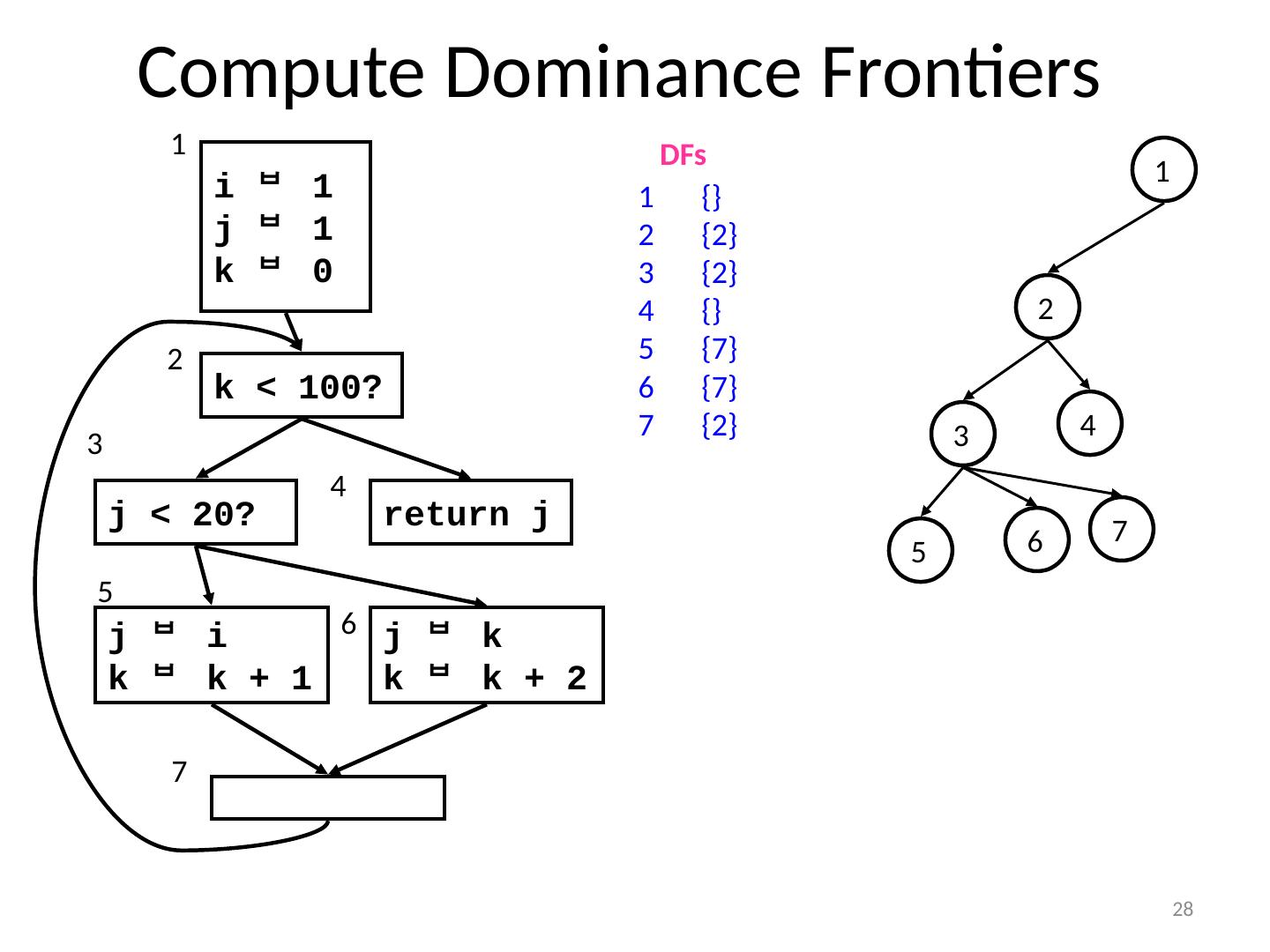
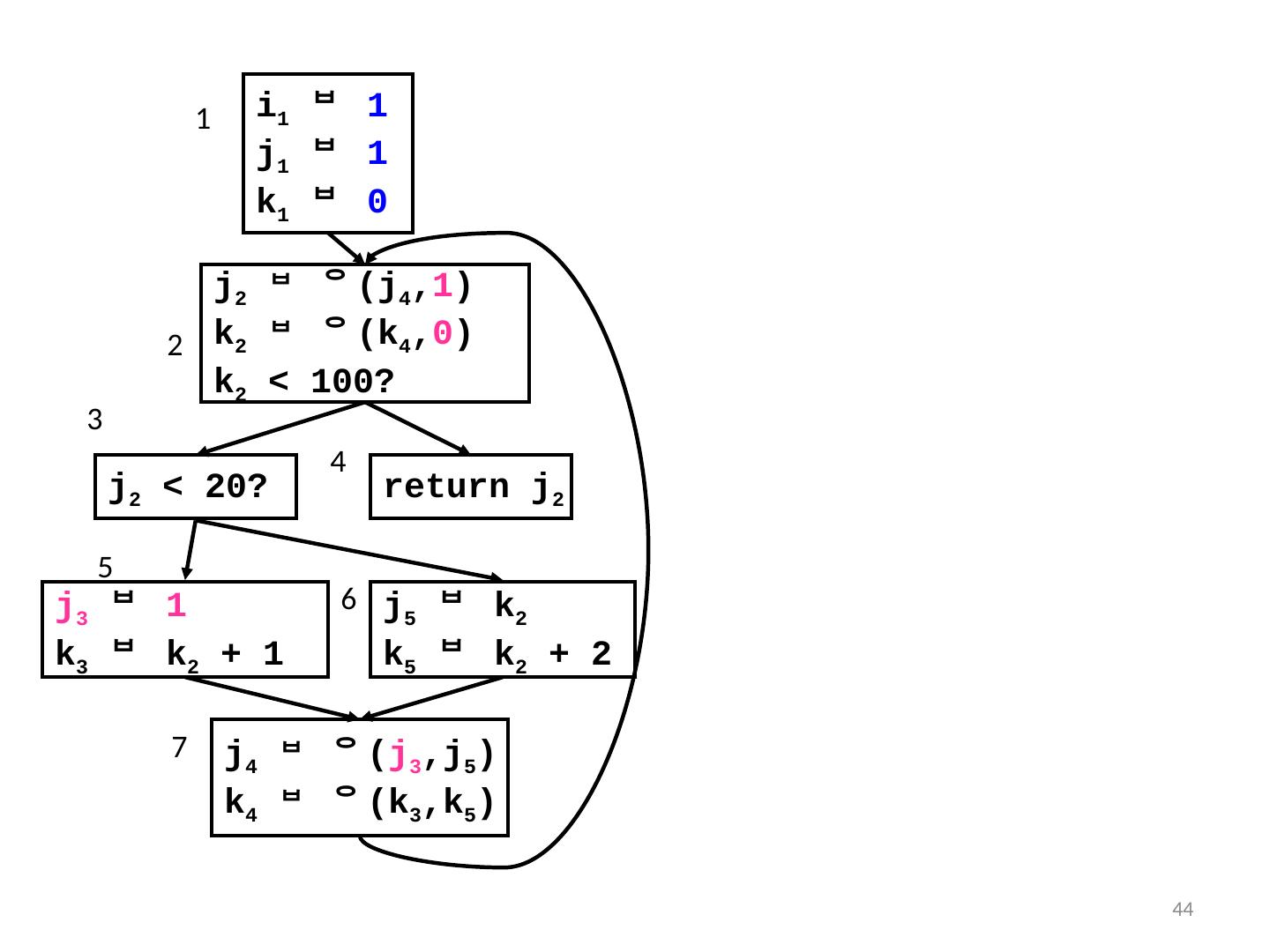
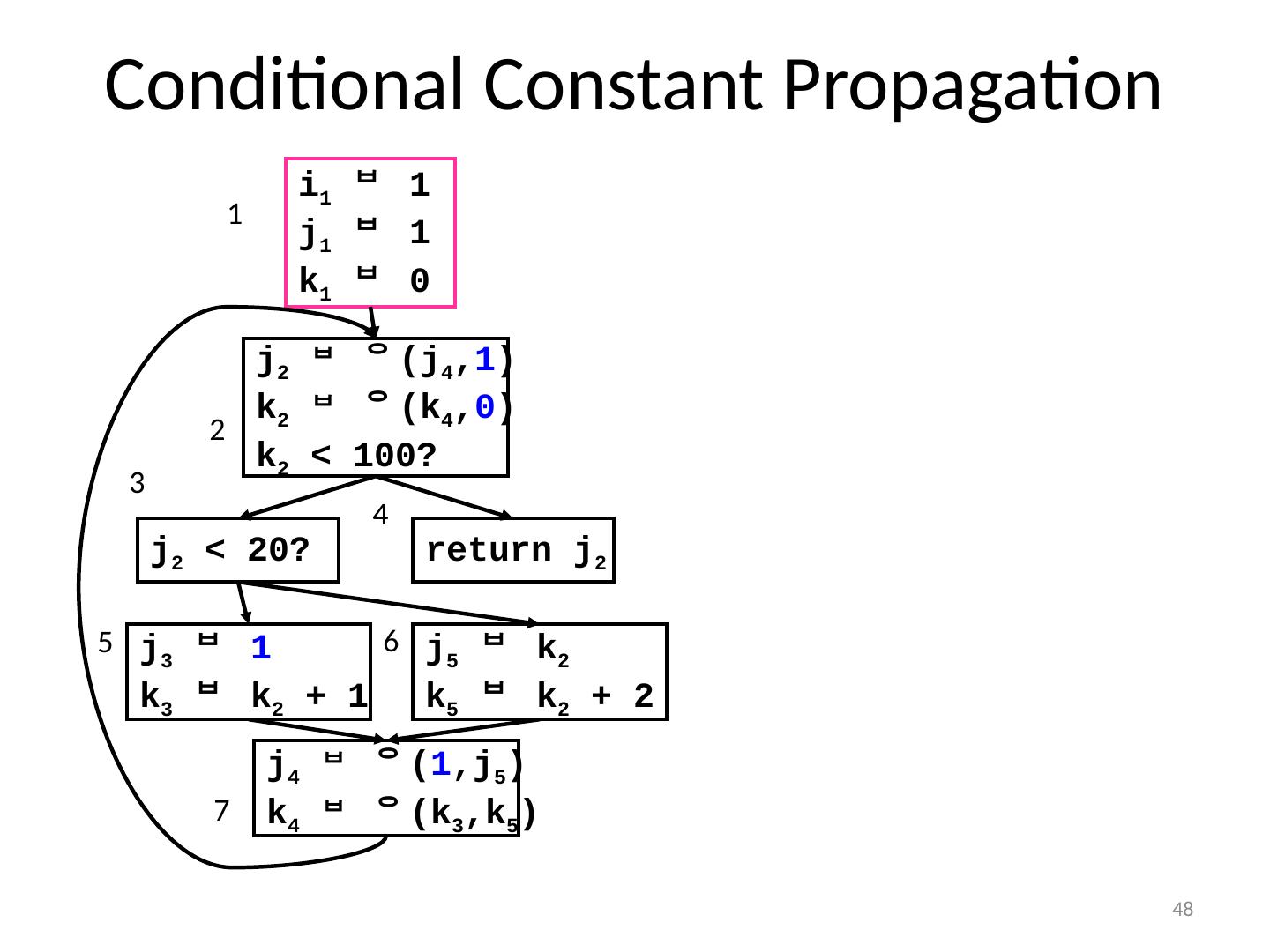
28 .28 Compute Dominance Frontiers i  1 j  1 k  0 k < 100? j < 20? return j j  i k  k + 1 j  k k  k + 2 1 2 4 6 5 7 1 5 6 7 2 3 4 DFs {} {2} {2} {} {7} {7} {2} 3

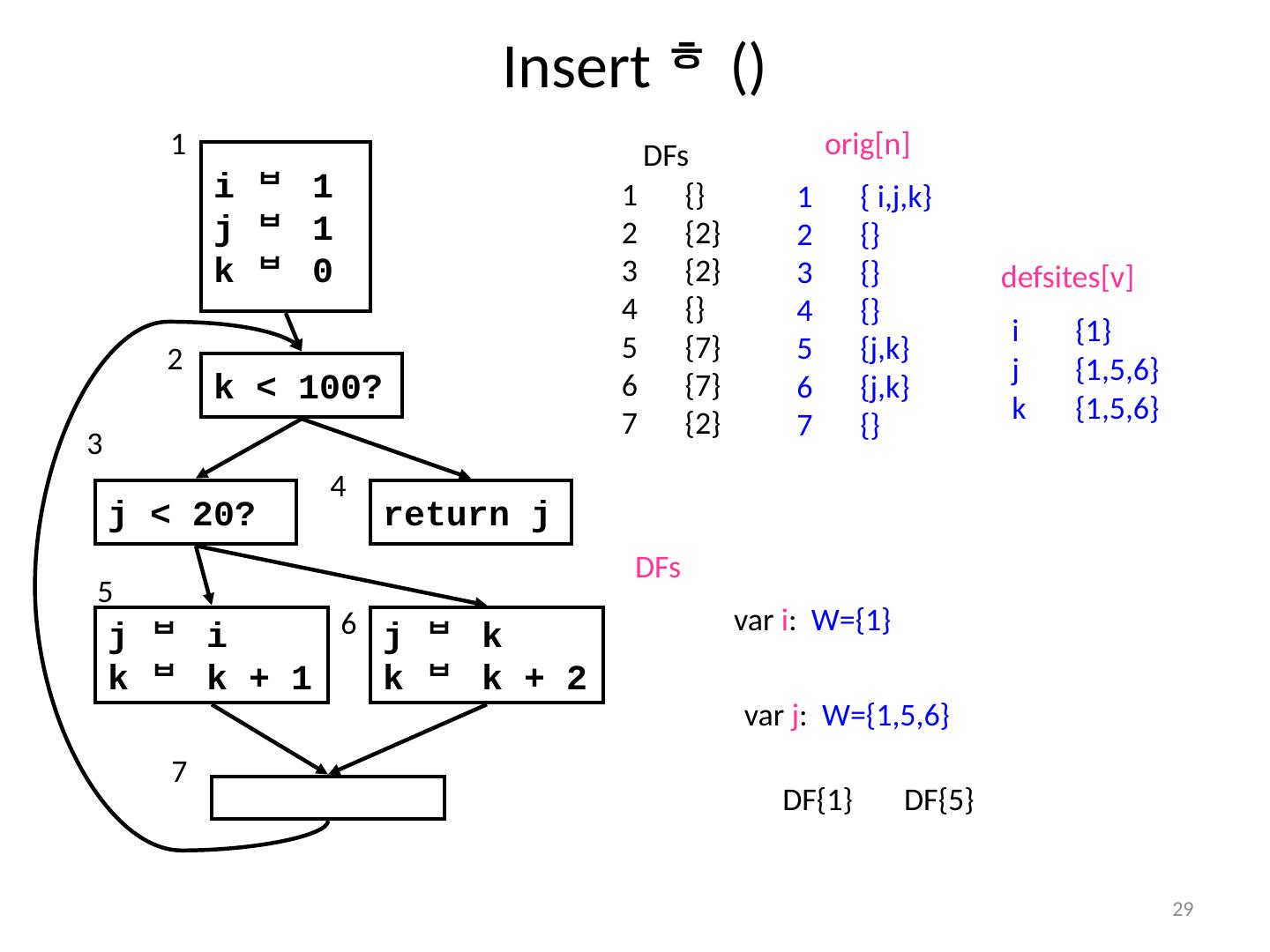
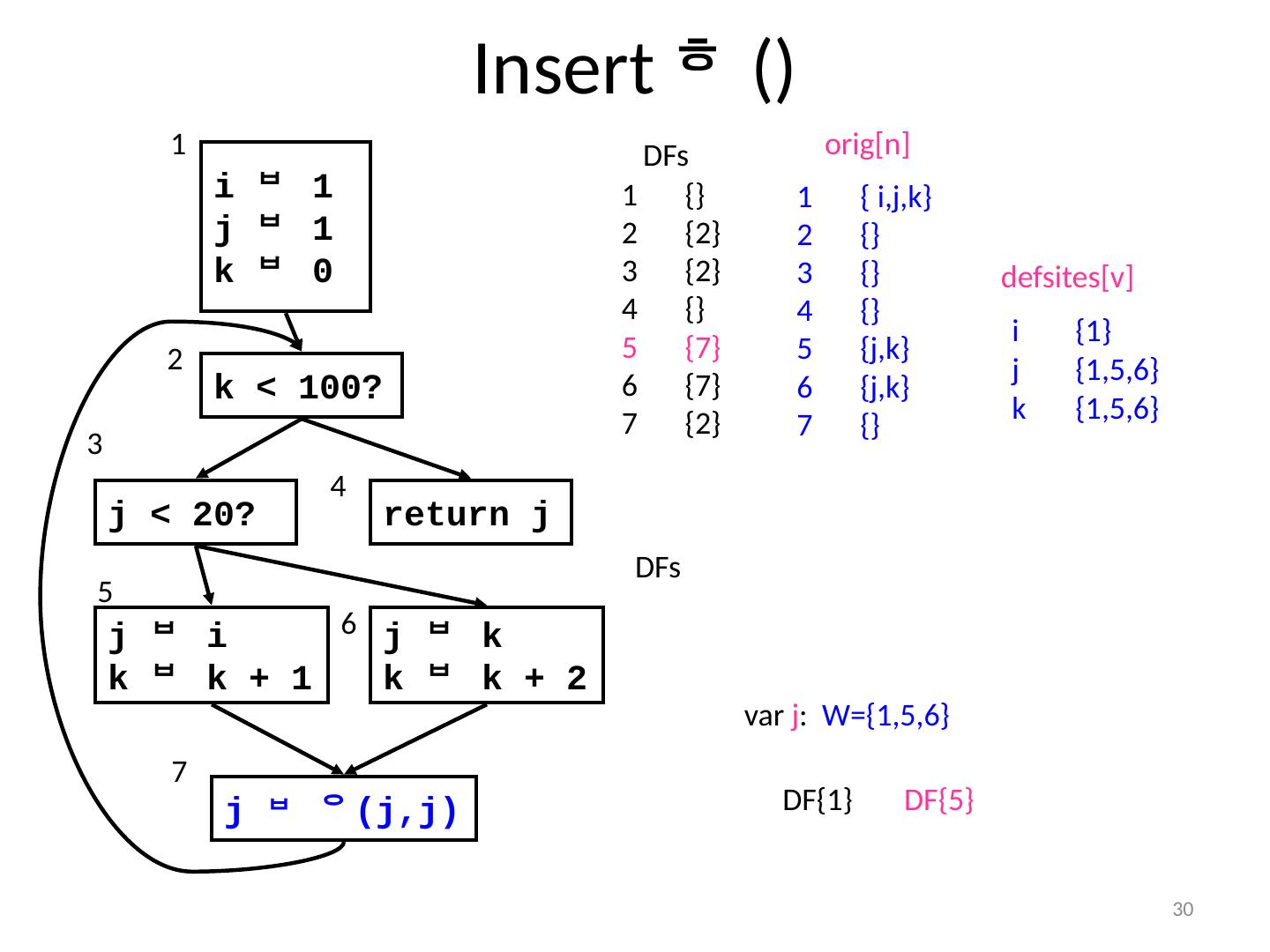
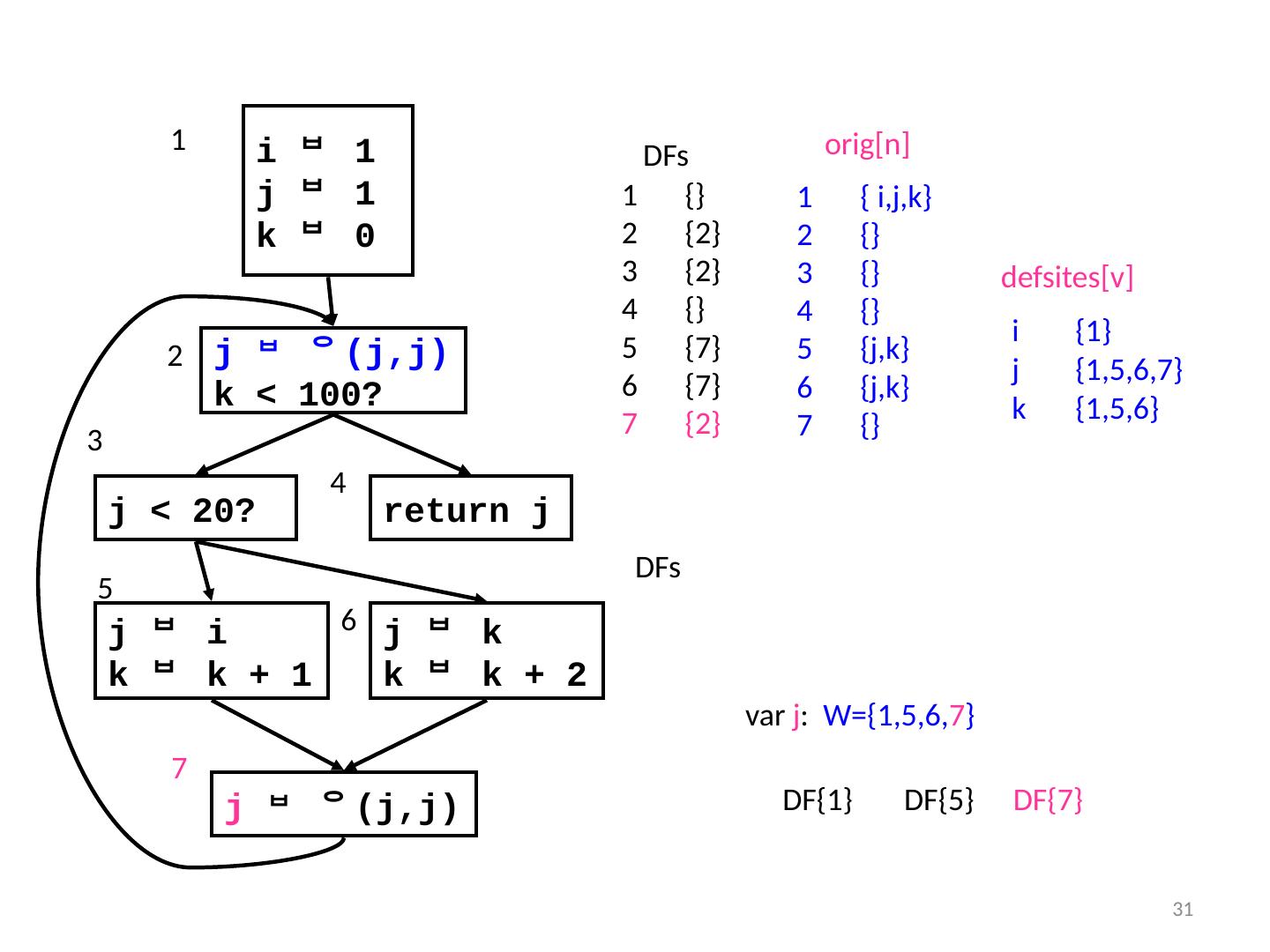
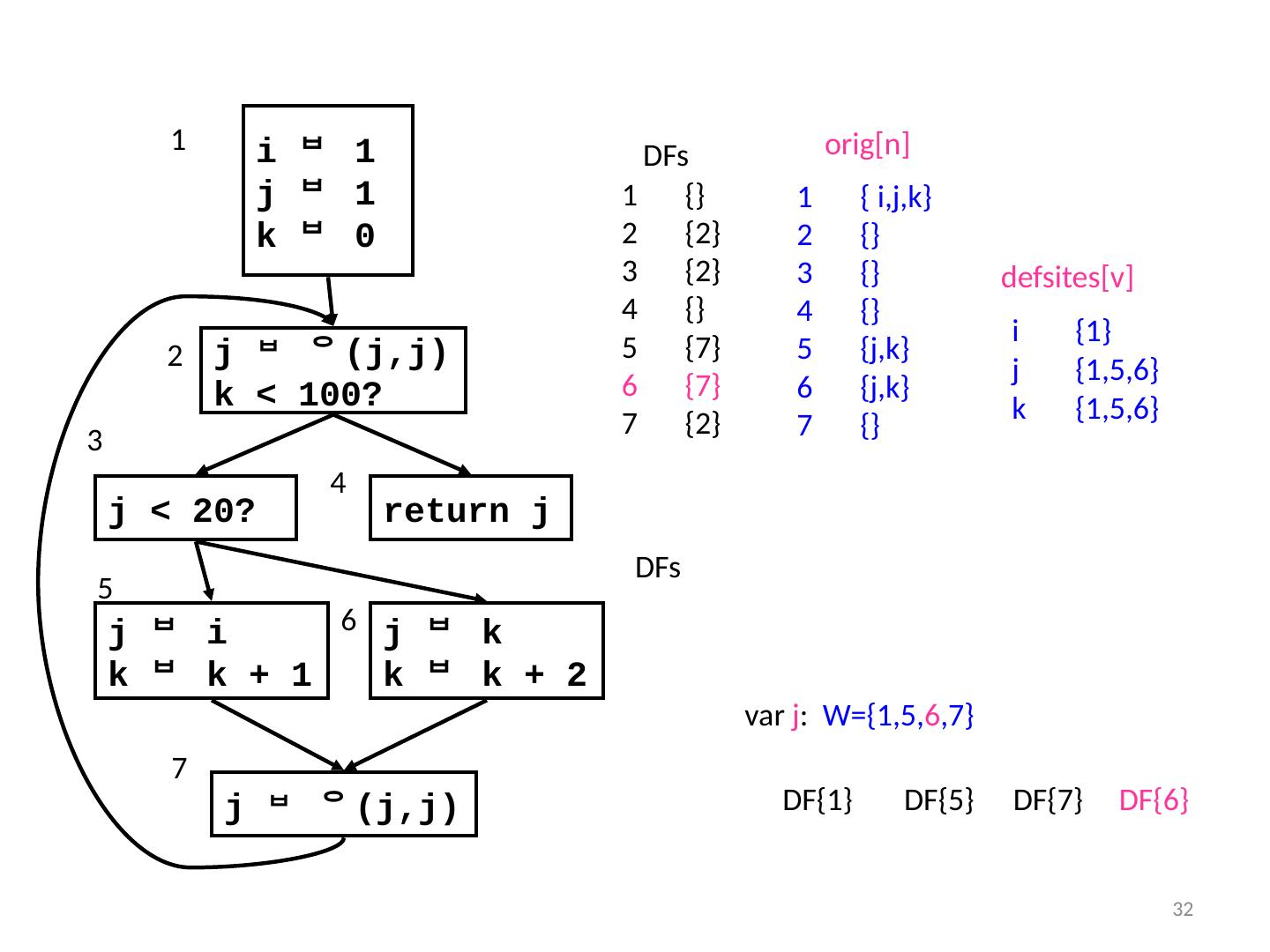
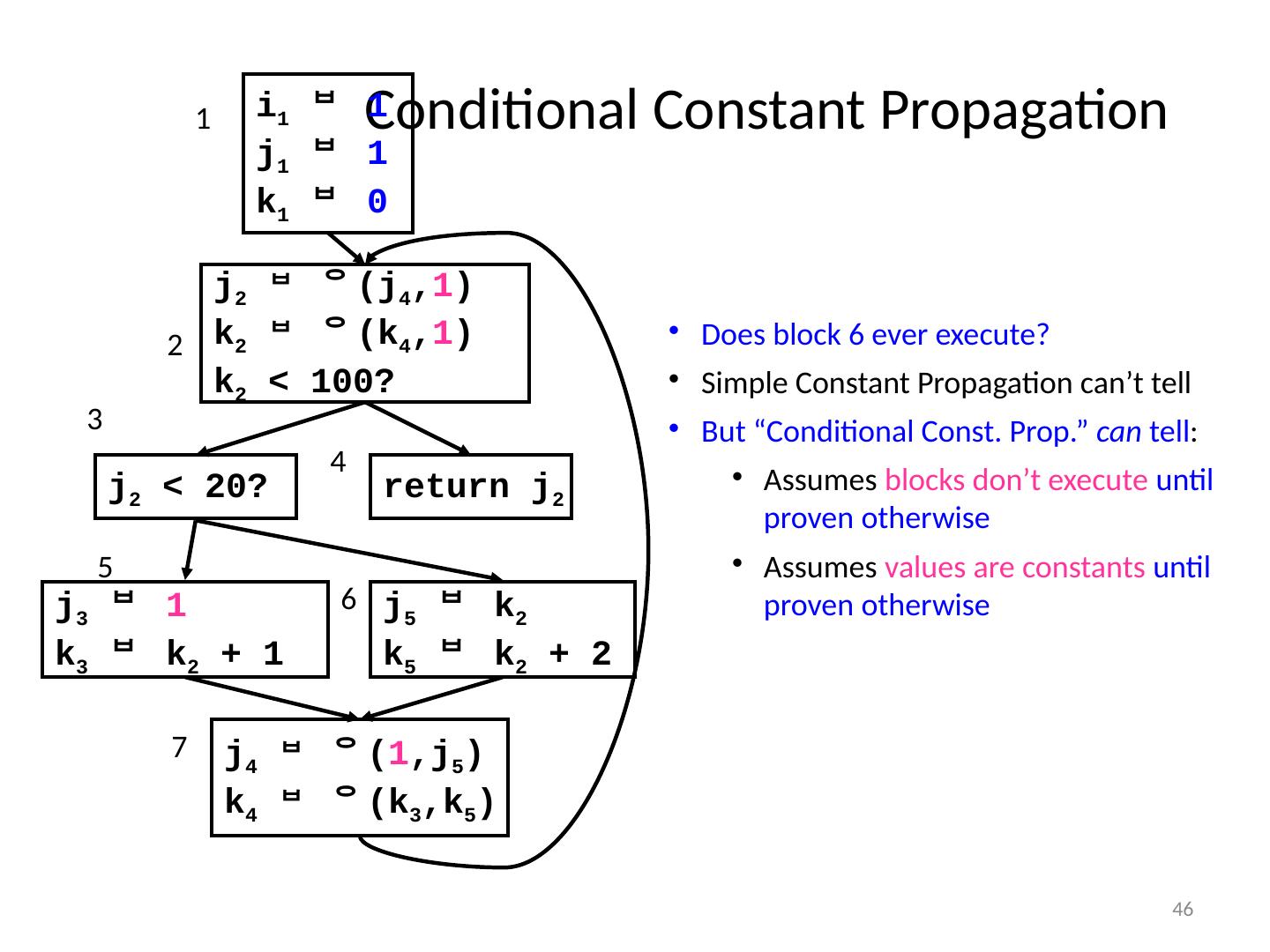
29 .29 Insert () i  1 j  1 k  0 k < 100? j < 20? return j j  i k  k + 1 j  k k  k + 2 1 2 4 6 5 7 DFs 3 { i,j,k } {} {} {} { j,k } { j,k } {} orig [n] defsites [v] i {1} j {1,5,6} k {1,5,6} var i : W={1} var j : W={1,5,6} DF{1} DFs {} {2} {2} {} {7} {7} {2} DF{5} DF{1}