Lecture 1 编译原理介绍

1 .CSC D70: Compiler Optimization Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Phillip Gibbons

2 .CSC D70: Compiler Optimization Introduction, Logistics Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Phillip Gibbons

3 .Summary Syllabus Course Introduction, Logistics, Grading Information Sheet Getting to know each other Assignments Learning LLVM Compiler Basics 3

4 .Syllabus: Who Are We? 4

5 .Gennady (Gena) Pekhimenko Assistant Professor, Instructor pekhimenko@cs.toronto.edu http://www.cs.toronto.edu/~pekhimenko/ Office: BA 5232 / IC 454 PhD from Carnegie Mellon Worked at Microsoft Research, NVIDIA, IBM Research interests: computer architecture, systems, machine learning, compilers, hardware acceleration, bioinformatics Computer Systems and Networking Group (CSNG) EcoSystem Group

6 .Bojian Zheng MSc. Student, TA bojian@cs.toronto.edu Office: BA 5214 D02 BSc. from UofT ECE Research interests: computer architecture, GPUs, machine learning Computer Systems and Networking Group (CSNG) EcoSystem Group

7 .Course Information: Where to Get? Course Website: http://www.cs.toronto.edu/~pekhimenko/courses/cscd70-w18/ Announcements, Syllabus, Course Info, Lecture Notes, Tutorial Notes, Assignments Piazza: https://piazza.com/utoronto.ca/winter2018/cscd70/home Questions/Discussions, Syllabus, Announcements Blackboard Emails/announcements Your email 7

8 .Useful Textbook 8

9 .CSC D70: Compiler Optimization Compiler Introduction Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Phillip Gibbons

10 .Introduction to Compilers What would you get out of this course? Structure of a Compiler Optimization Example 10

11 .What Do Compilers Do? Translate one language into another e.g., convert C++ into x86 object code difficult for “natural” languages, but feasible for computer languages Improve (i.e. “optimize”) the code e.g., make the code run 3 times faster or more energy efficient, more robust, etc. driving force behind modern processor design 11

12 .How Can the Compiler Improve Performance? Execution time = Operation count * Machine cycles per operation Minimize the number of operations arithmetic operations, memory accesses Replace expensive operations with simpler ones e.g., replace 4-cycle multiplication with 1-cycle shift Minimize cache misses both data and instruction accesses Perform work in parallel instruction scheduling within a thread parallel execution across multiple threads 12

13 .What Would You Get Out of This Course? Basic knowledge of existing compiler optimizations Hands-on experience in constructing optimizations within a fully functional research compiler Basic principles and theory for the development of new optimizations 13

14 .Structure of a Compiler Optimizations are performed on an “ intermediate form ” similar to a generic RISC instruction set Allows easy portability to multiple source languages, target machines 14 x86 ARM SPARC MIPS

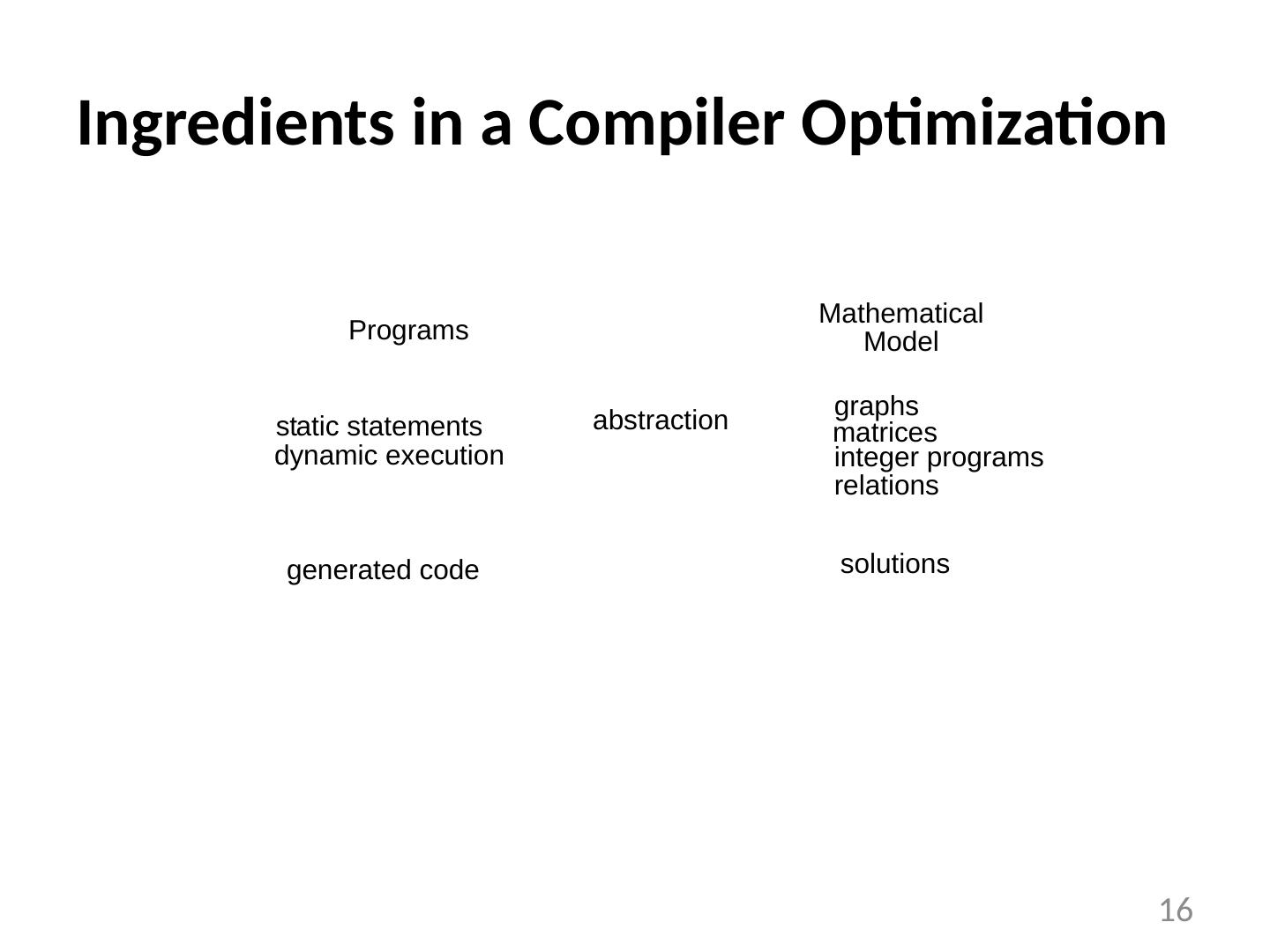
15 .Ingredients in a Compiler Optimization Formulate optimization problem Identify opportunities of optimization applicable across many programs affect key parts of the program (loops/recursions) amenable to “efficient enough” algorithm Representation Must abstract essential details relevant to optimization 15

16 .Ingredients in a Compiler Optimization 16

17 .Ingredients in a Compiler Optimization Formulate optimization problem Identify opportunities of optimization applicable across many programs affect key parts of the program (loops/recursions) amenable to “efficient enough” algorithm Representation Must abstract essential details relevant to optimization Analysis Detect when it is desirable and safe to apply transformation Code Transformation Experimental Evaluation (and repeat process) 17

18 .Representation: Instructions Three-address code A := B op C LHS: name of variable e.g. x, A[t] (address of A + contents of t ) RHS: value Typical instructions A := B op C A := unaryop B A := B GOTO s IF A relop B GOTO s CALL f RETURN 18

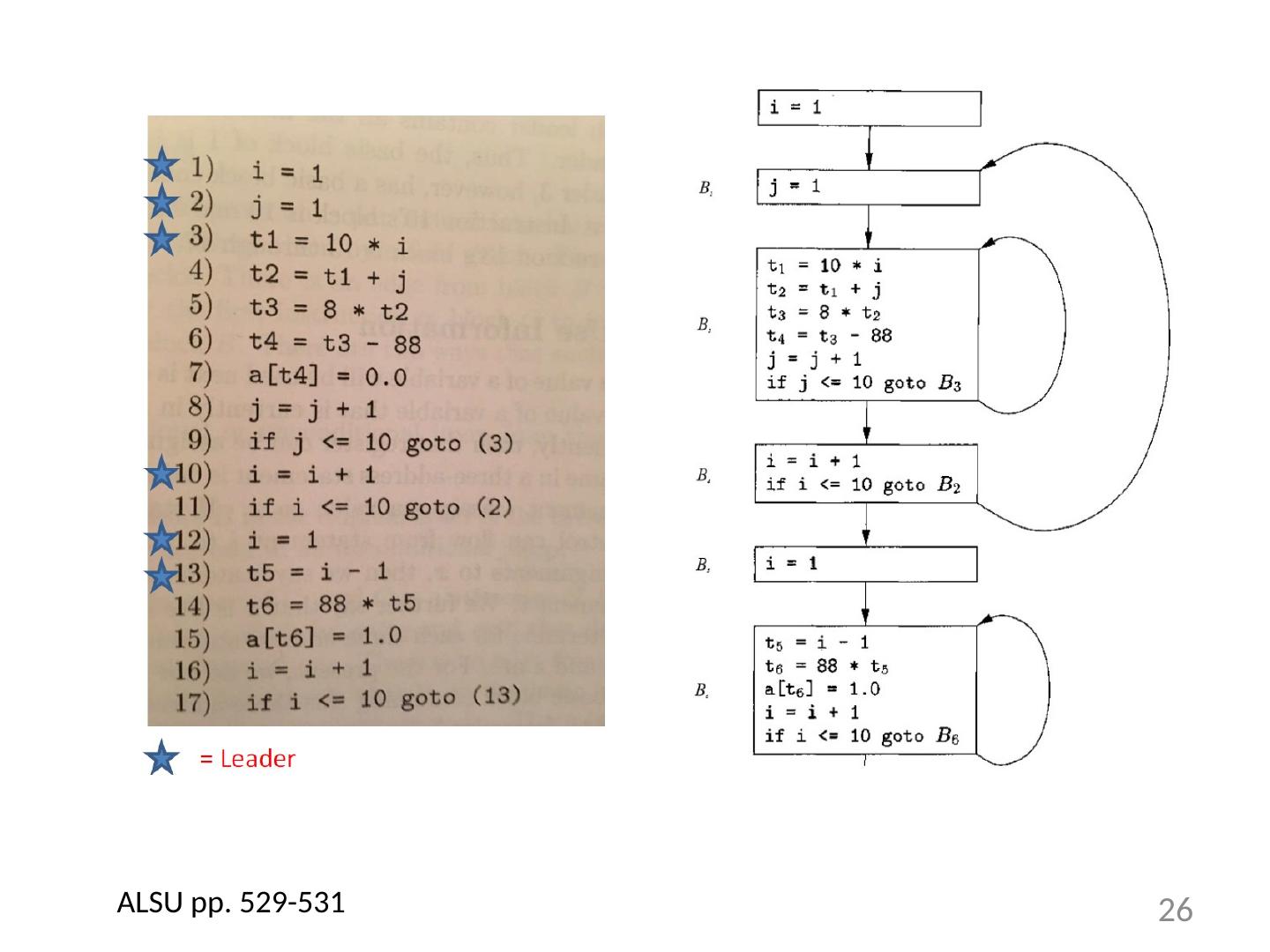
19 .Optimization Example Bubblesort program that sorts an array A that is allocated in static storage: an element of A requires four bytes of a byte-addressed machine elements of A are numbered 1 through n ( n is a variable) A[j] is in location &A+4*(j-1) FOR i := n-1 DOWNTO 1 DO FOR j := 1 TO i DO IF A[j]> A[j+1] THEN BEGIN temp := A[j]; A[j] := A[j+1]; A[j+1] := temp END 19

20 .Translated Code i := n-1 S5: if i <1 goto s1 j := 1 s4: if j> i goto s2 t1 := j-1 t2 := 4*t1 t3 := A[t2] ;A[j] t4 := j+1 t5 := t4-1 t6 := 4*t5 t7 := A[t6] ;A[j+1] if t3<=t7 goto s3 t8 :=j-1 t9 := 4*t8 temp := A[t9] ;A[j] t10 := j+1 t11:= t10-1 t12 := 4*t11 t13 := A[t12] ;A[j+1] t14 := j-1 t15 := 4*t14 A[t15] := t13 ;A[j]:=A[j+1] t16 := j+1 t17 := t16-1 t18 := 4*t17 A[t18]:=temp ;A[j+1]:=temp s3: j := j+1 goto S4 S2: i := i-1 goto s5 s1: 20 FOR i := n-1 DOWNTO 1 DO FOR j := 1 TO i DO IF A[j]> A[j+1] THEN BEGIN temp := A[j]; A[j] := A[j+1]; A[j+1] := temp END

21 .Representation: a Basic Block Basic block = a sequence of 3-address statements only the first statement can be reached from outside the block (no branches into middle of block) all the statements are executed consecutively if the first one is (no branches out or halts except perhaps at end of block) We require basic blocks to be maximal they cannot be made larger without violating the conditions Optimizations within a basic block are local optimizations 21

22 .Flow Graphs Nodes : basic blocks Edges : B i -> B j , iff B j can follow B i immediately in some execution Either first instruction of B j is target of a goto at end of B i Or, B j physically follows B i, which does not end in an unconditional goto . The block led by first statement of the program is the start , or entry node. 22

23 .Find the Basic Blocks i := n-1 S5: if i <1 goto s1 j := 1 s4: if j> i goto s2 t1 := j-1 t2 := 4*t1 t3 := A[t2] ;A[j] t4 := j+1 t5 := t4-1 t6 := 4*t5 t7 := A[t6] ;A[j+1] if t3<=t7 goto s3 t8 :=j-1 t9 := 4*t8 temp := A[t9] ;A[j] t10 := j+1 t11:= t10-1 t12 := 4*t11 t13 := A[t12] ;A[j+1] t14 := j-1 t15 := 4*t14 A[t15] := t13 ;A[j]:=A[j+1] t16 := j+1 t17 := t16-1 t18 := 4*t17 A[t18]:=temp ;A[j+1]:=temp s3: j := j+1 goto S4 S2: i := i-1 goto s5 s1: 23

24 .Basic Blocks from Example 24

25 .Partitioning into Basic Blocks Identify the leader of each basic block First instruction Any target of a jump Any instruction immediately following a jump Basic block starts at leader & ends at instruction immediately before a leader (or the last instruction) 25

26 .26 ALSU pp. 529-531

27 .Sources of Optimizations Algorithm optimization Algebraic optimization A := B+0 => A := B Local optimizations within a basic block -- across instructions Global optimizations within a flow graph -- across basic blocks Interprocedural analysis within a program -- across procedures (flow graphs) 27

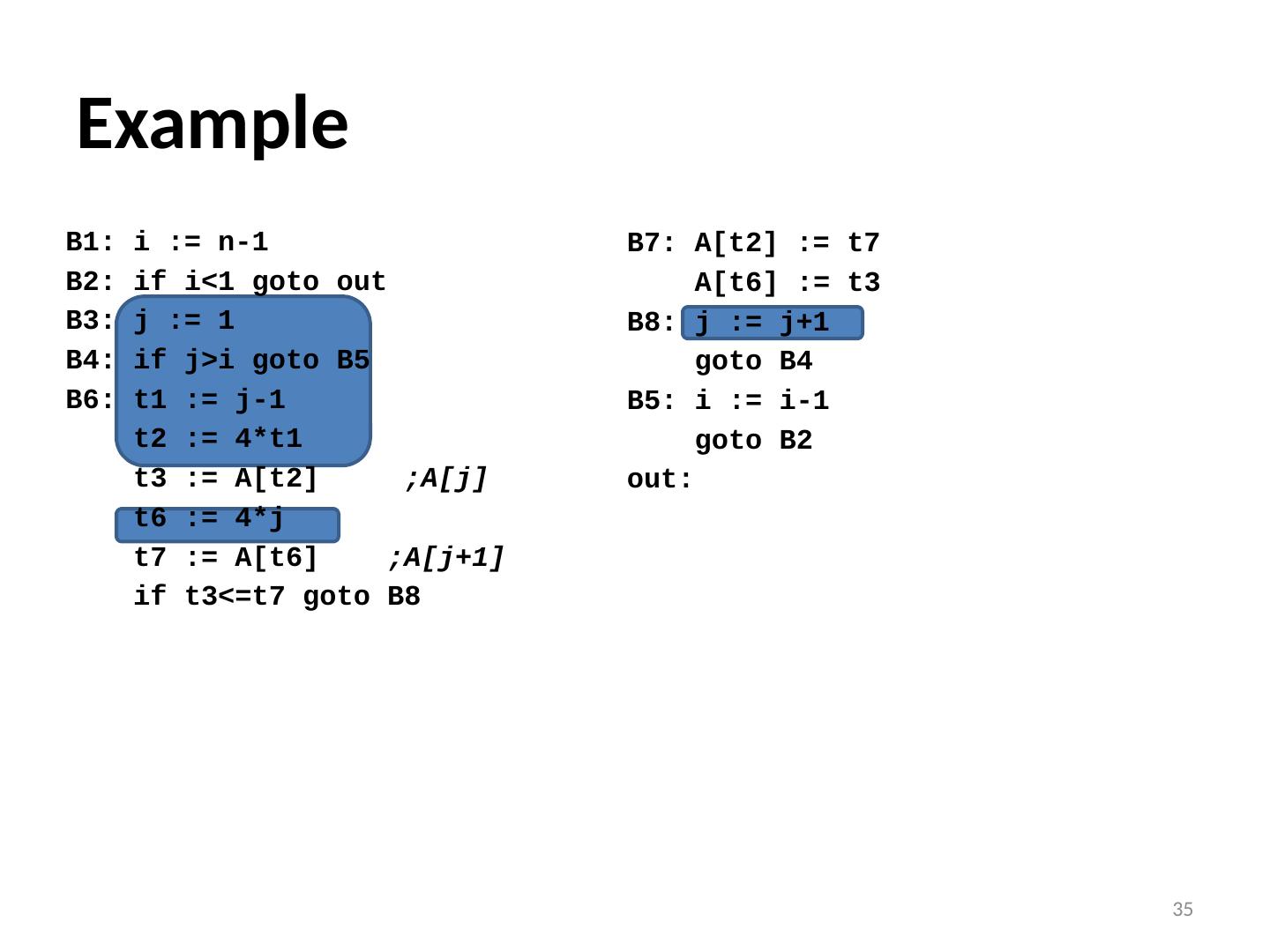
28 .Local Optimizations Analysis & transformation performed within a basic block No control flow information is considered Examples of local optimizations: local common subexpression elimination analysis: same expression evaluated more than once in b. transformation: replace with single calculation local constant folding or elimination analysis: expression can be evaluated at compile time transformation: replace by constant, compile-time value dead code elimination 28

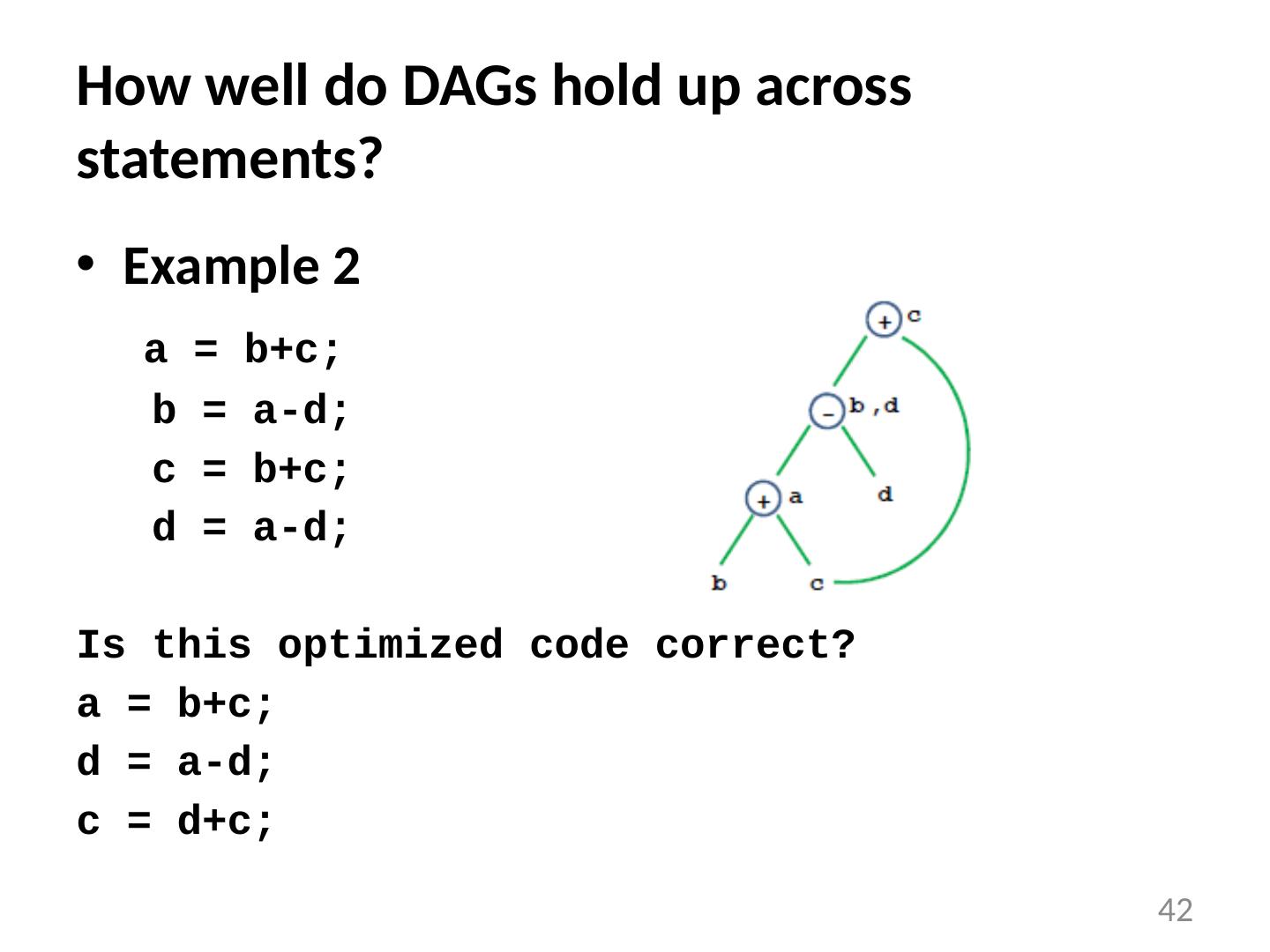
29 . i := n-1 S5: if i <1 goto s1 j := 1 s4: if j> i goto s2 t1 := j-1 t2 := 4*t1 t3 := A[t2] ;A[j] t4 := j+1 t5 := t4-1 t6 := 4*t5 t7 := A[t6] ;A[j+1] if t3<=t7 goto s3 Example 29 t8 :=j-1 t9 := 4*t8 temp := A[t9] ;A[j] t10 := j+1 t11:= t10-1 t12 := 4*t11 t13 := A[t12] ;A[j+1] t14 := j-1 t15 := 4*t14 A[t15] := t13 ;A[j]:=A[j+1] t16 := j+1 t17 := t16-1 t18 := 4*t17 A[t18]:=temp ;A[j+1]:=temp s3: j := j+1 goto S4 S2: i := i-1 goto s5 s1: