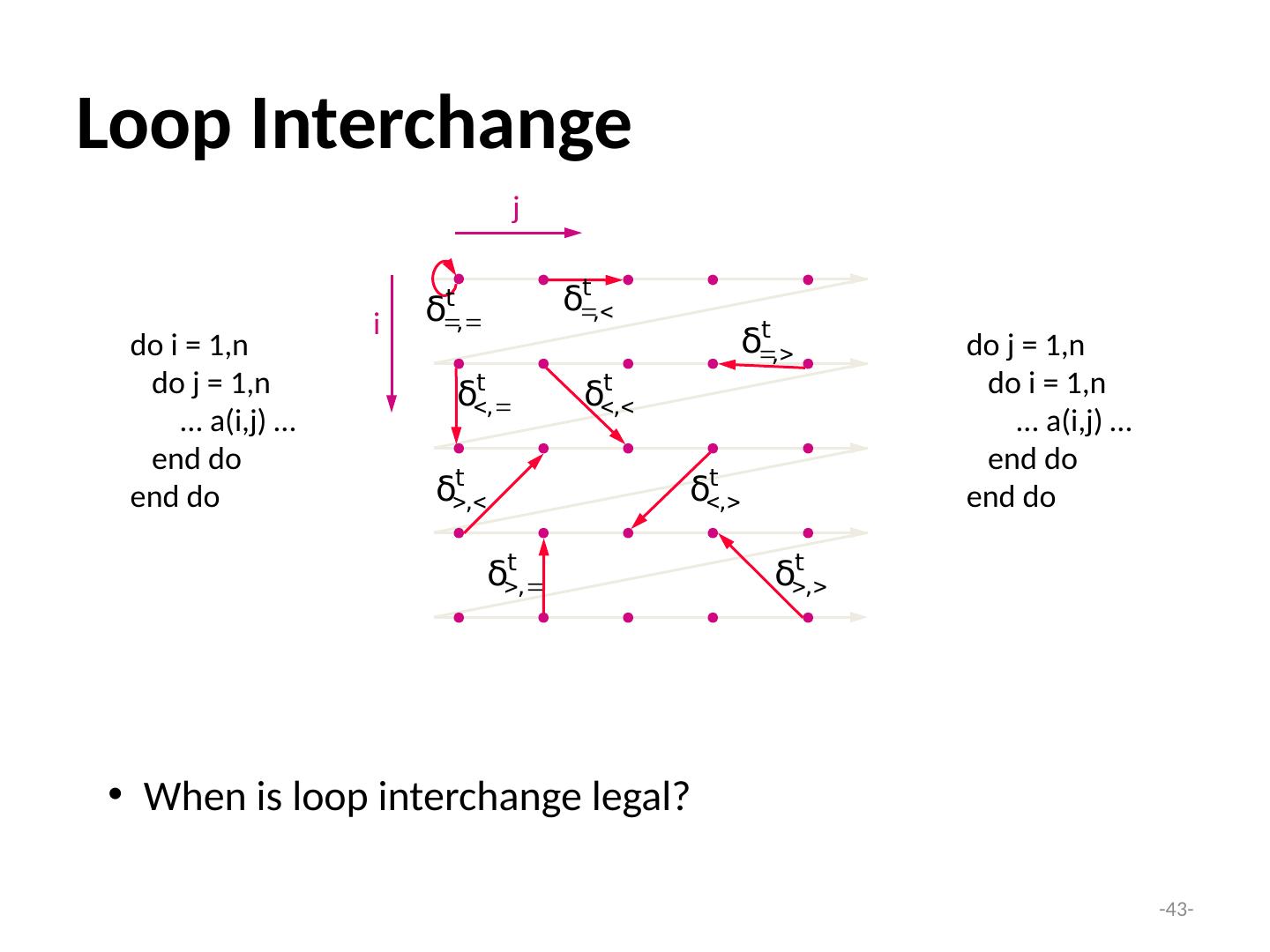
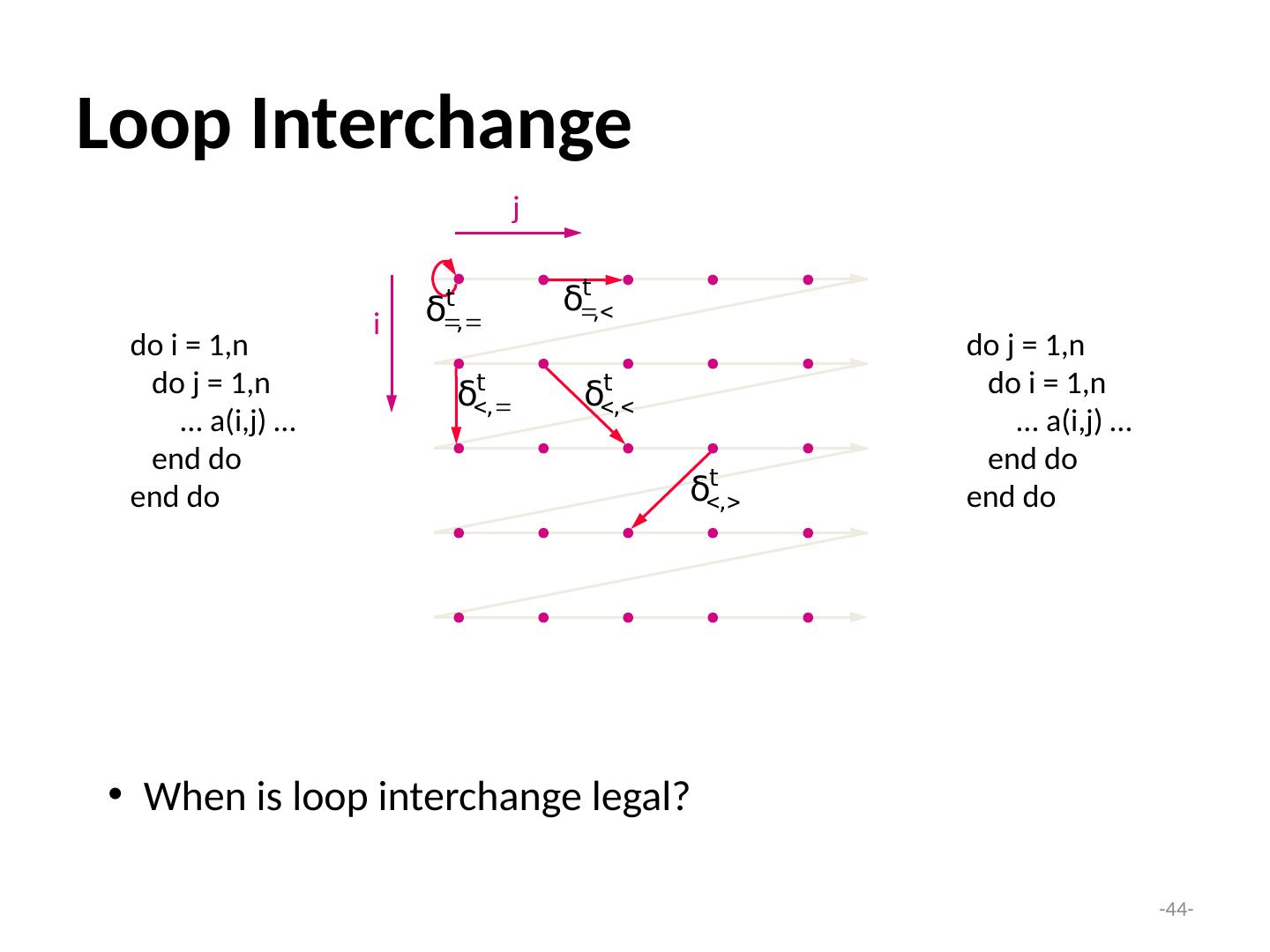
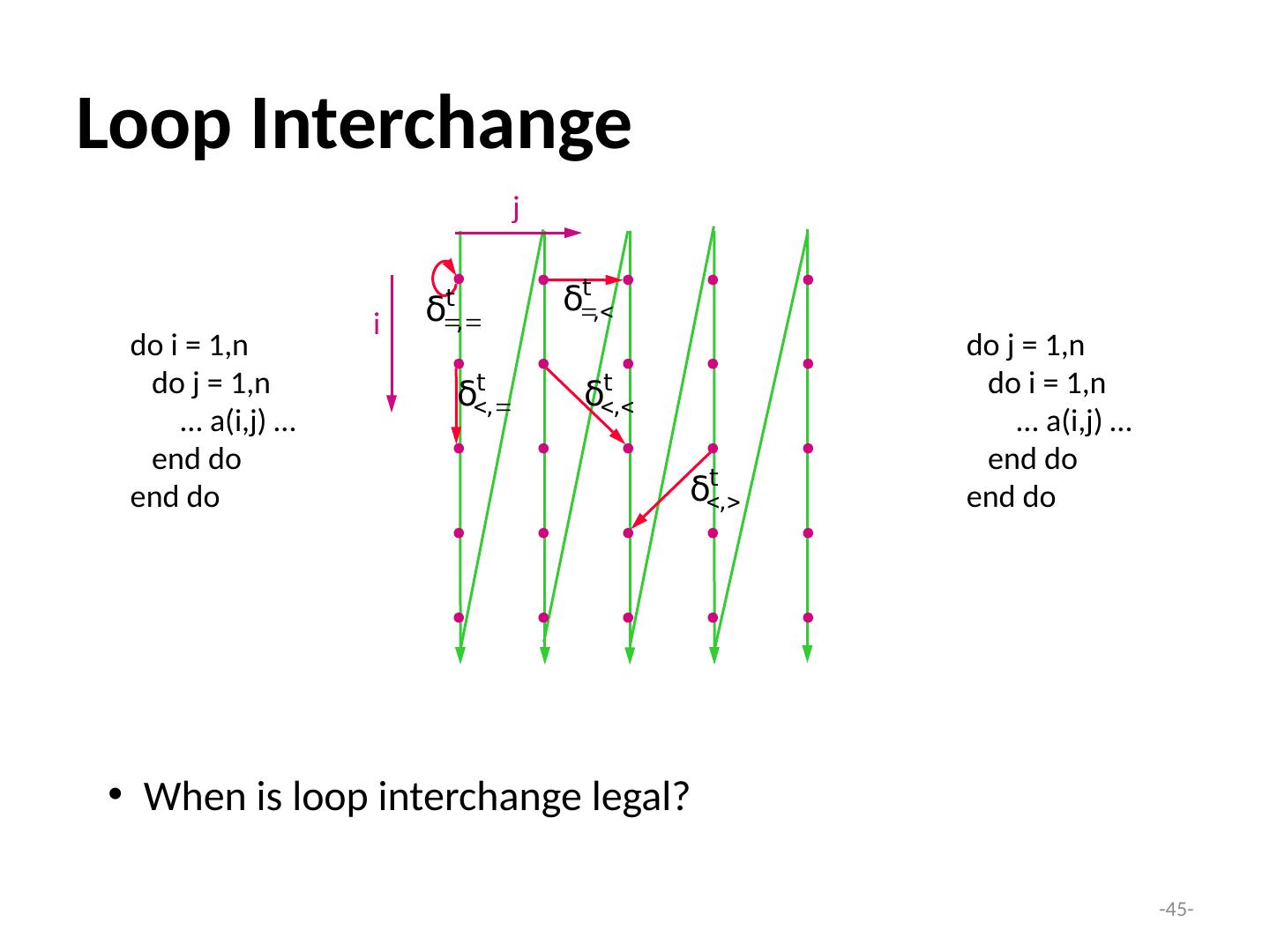
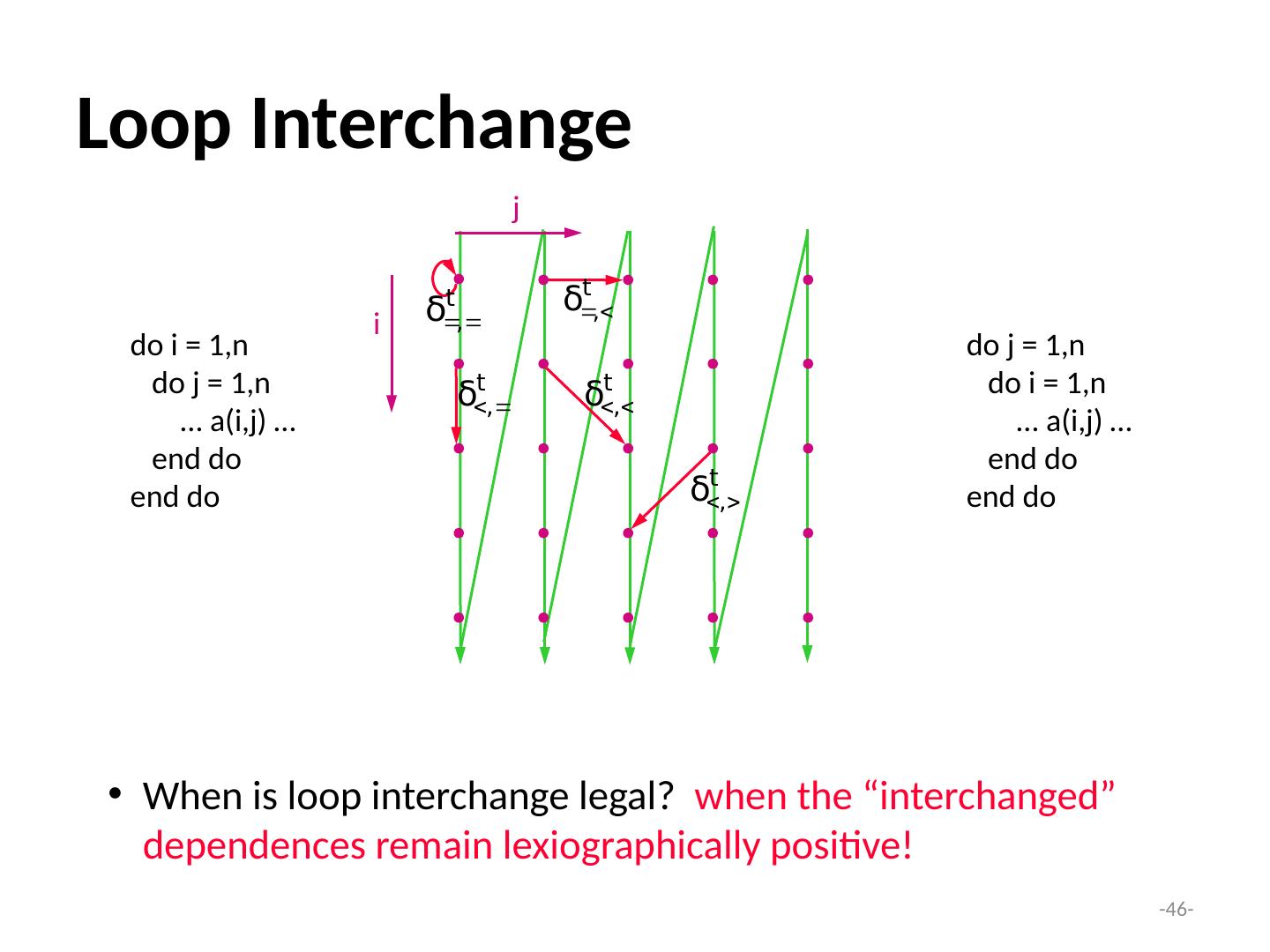
Lecture 10 并行化

1 .CSC D70: Compiler Optimization Parallelization Prof. Gennady Pekhimenko University of Toronto Winter 2018 The content of this lecture is adapted from the lectures of Todd Mowry and Tarek Abdelrahman

2 .Announcements Final exam: Wednesday, April 11 , 7:00-8:30pm ; Room: IC120 Covers the whole semester Course evaluation (right now) 2

3 .- 3 - Flow (true) dependence : a statement S i precedes a statement S j in execution and S i computes a data value that S j uses. Implies that S i must execute before S j . We define four types of data dependence. Data Dependence

4 .- 4 - Anti dependence : a statement S i precedes a statement S j in execution and S i uses a data value that S j computes. It implies that S i must be executed before S j . We define four types of data dependence. Data Dependence

5 .- 5 - Output dependence : a statement S i precedes a statement S j in execution and S i computes a data value that S j also computes. It implies that S i must be executed before S j . We define four types of data dependence. Data Dependence

6 .- 6 - Input dependence : a statement S i precedes a statement S j in execution and S i uses a data value that S j also uses. Does this imply that S i must execute before S j ? We define four types of data dependence. Data Dependence

7 .- 7 - Data Dependence (continued) The dependence is said to flow from S i to S j because S i precedes S j in execution. S i is said to be the source of the dependence. S j is said to be the sink of the dependence. The only “true” dependence is flow dependence; it represents the flow of data in the program. The other types of dependence are caused by programming style; they may be eliminated by re-naming.

8 .- 8 - Data Dependence (continued) Data dependence in a program may be represented using a dependence graph G=(V,E), where the nodes V represent statements in the program and the directed edges E represent dependence relations. S 1 S 2 S 3 S 4 d t d a d o d o d t d I

9 .- 9 - Value or Location? There are two ways a dependence is defined: value-oriented or location-oriented .

10 .- 10 - Example 1 do i = 2, 4 S 1 : a(i) = b(i) + c(i) S 2 : d(i) = a(i) end do S 1 [2] S 2 [2] S 1 [3] S 2 [3] S 1 [4] S 2 [4] i=2 i=3 i=4 a(2) a(2) a(3) a(3) a(4) a(4) d t d t d t There is an instance of S 1 that precedes an instance of S 2 in execution and S 1 produces data that S 2 consumes. S 1 is the source of the dependence; S 2 is the sink of the dependence. The dependence flows between instances of statements in the same iteration ( loop-independent dependence). The number of iterations between source and sink ( dependence distance ) is 0. The dependence direction is = . or

11 .- 11 - Example 2 do i = 2, 4 S 1 : a(i) = b(i) + c(i) S 2 : d(i) = a(i-1) end do S 1 [2] S 2 [2] S 1 [3] S 2 [3] S 1 [4] S 2 [4] i=2 i=3 i=4 a(2) a(1) a(3) a(2) a(4) a(3) d t d t There is an instance of S 1 that precedes an instance of S 2 in execution and S 1 produces data that S 2 consumes. S 1 is the source of the dependence; S 2 is the sink of the dependence. The dependence flows between instances of statements in different iterations ( loop-carried dependence). The dependence distance is 1. The direction is positive ( < ). or

12 .- 12 - Example 3 do i = 2, 4 S 1 : a(i) = b(i) + c(i) S 2 : d(i) = a(i+1) end do S 1 [2] S 2 [2] S 1 [3] S 2 [3] S 1 [4] S 2 [4] i=2 i=3 i=4 a(2) a(3) a(3) a(4) a(4) a(5) d a d a or There is an instance of S 2 that precedes an instance of S 1 in execution and S 2 consumes data that S 1 produces. S 2 is the source of the dependence; S 1 is the sink of the dependence. The dependence is loop-carried. The dependence distance is 1. Are you sure you know why it is even though S 1 appears before S 2 in the code? 1 a 2 S S < d

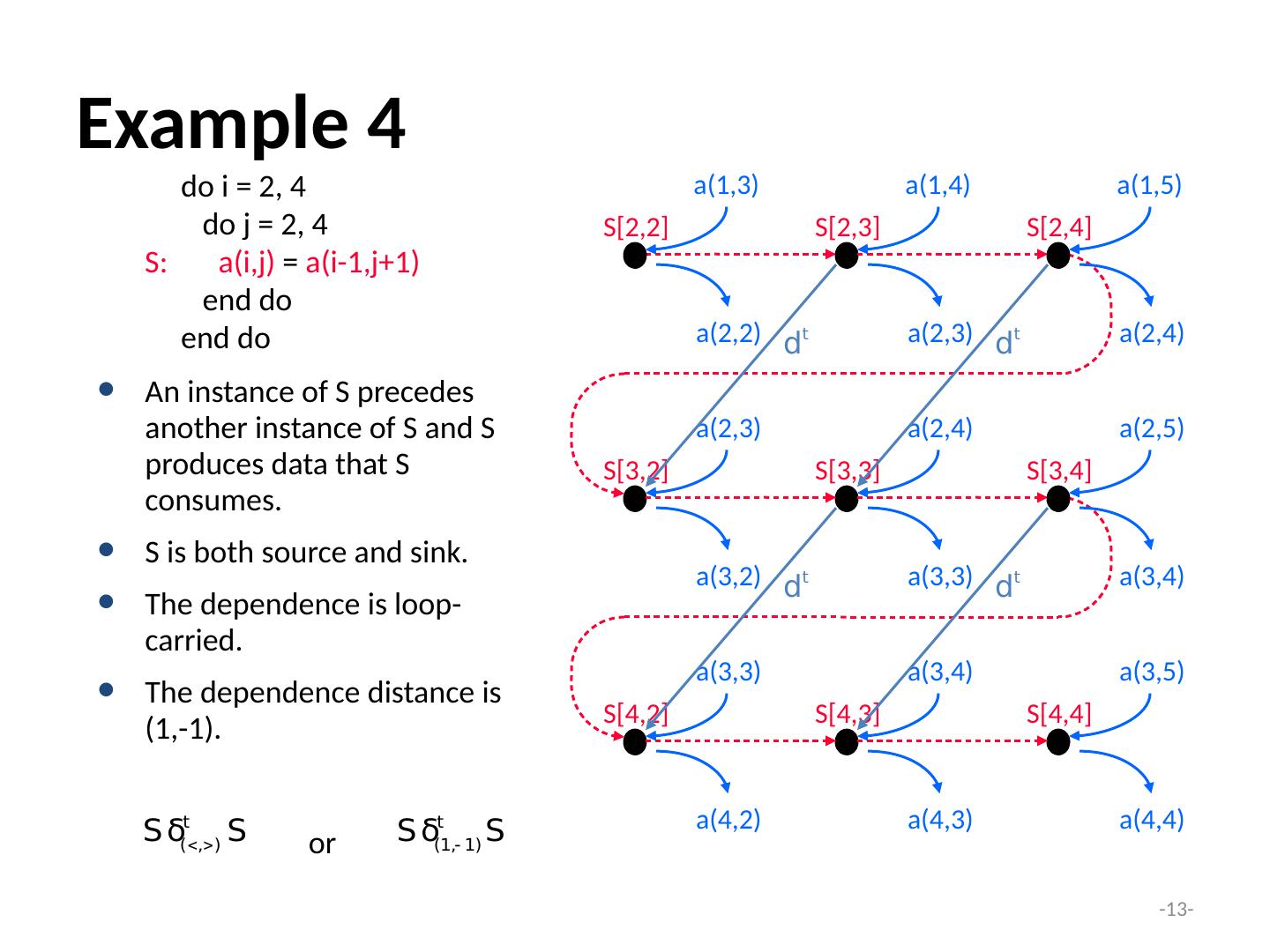
13 .- 13 - Example 4 do i = 2, 4 do j = 2, 4 S: a(i,j) = a(i-1,j+1) end do end do S[2,2] S[2,3] S[2,4] S[3,2] S[4,2] S[3,3] S[4,3] S[3,4] S[4,4] a(1,3) a(1,4) a(1,5) a(2,3) a(2,4) a(2,5) a(3,3) a(3,4) a(3,5) a(2,2) a(2,3) a(2,4) a(3,2) a(3,3) a(3,4) a(4,2) a(4,3) a(4,4) d t d t d t d t An instance of S precedes another instance of S and S produces data that S consumes. S is both source and sink. The dependence is loop-carried. The dependence distance is (1,-1). or

14 .- 14 - Problem Formulation Consider the following perfect nest of depth d: subscript position array reference subscript function or subscript expression

15 .- 15 - Problem Formulation Dependence will exist if there exists two iteration vectors and such that and: That is: and and and and and and

16 .- 16 - Problem Formulation - Example Does there exist two iteration vectors i 1 and i 2 , such that 2 £ i 1 £ i 2 £ 4 and such that: i 1 = i 2 -1? Answer: yes; i 1 =2 & i 2 =3 and i 1 =3 & i 2 =4. Hence, there is dependence! The dependence distance vector is i 2 -i 1 = 1. The dependence direction vector is sign(1) = < . do i = 2, 4 S 1 : a( i ) = b( i ) + c( i ) S 2 : d( i ) = a(i-1) end do

17 .- 17 - Problem Formulation - Example Does there exist two iteration vectors i 1 and i 2 , such that 2 £ i 1 £ i 2 £ 4 and such that: i 1 = i 2 +1? Answer: yes; i 1 =3 & i 2 =2 and i 1 =4 & i 2 =3. (But, but!). Hence, there is dependence! The dependence distance vector is i 2 -i 1 = -1. The dependence direction vector is sign(-1) = > . Is this possible? do i = 2, 4 S 1 : a( i ) = b( i ) + c( i ) S 2 : d( i ) = a(i+1) end do

18 .- 18 - Problem Formulation - Example Does there exist two iteration vectors i 1 and i 2 , such that 1 £ i 1 £ i 2 £ 10 and such that: 2*i 1 = 2*i 2 +1? Answer: no; 2*i 1 is even & 2*i 2 +1 is odd. Hence, there is no dependence! do i = 1, 10 S 1 : a(2* i ) = b( i ) + c( i ) S 2 : d( i ) = a(2*i+1) end do

19 .- 19 - Problem Formulation Dependence testing is equivalent to an integer linear programming (ILP) problem of 2d variables & m+d constraint! An algorithm that determines if there exits two iteration vectors and that satisfies these constraints is called a dependence tester . The dependence distance vector is given by . The dependence direction vector is give by sign( ). Dependence testing is NP-complete! A dependence test that reports dependence only when there is dependence is said to be exact . Otherwise it is in-exact . A dependence test must be conservative ; if the existence of dependence cannot be ascertained, dependence must be assumed. - -

20 .- 20 - Dependence Testers Lamport’s Test. GCD Test. Banerjee’s Inequalities. Generalized GCD Test. Power Test. I-Test. Omega Test. Delta Test. Stanford Test. etc…

21 .- 21 - Lamport’s Test Lamport’s Test is used when there is a single index variable in the subscript expressions, and when the coefficients of the index variable in both expressions are the same. The dependence problem: does there exist i 1 and i 2 , such that L i £ i 1 £ i 2 £ U i and such that b*i 1 + c 1 = b*i 2 + c 2 ? or There is integer solution if and only if is integer. The dependence distance is d = if L i £ |d| £ U i . d > 0 Þ true dependence. d = 0 Þ loop independent dependence. d < 0 Þ anti dependence.

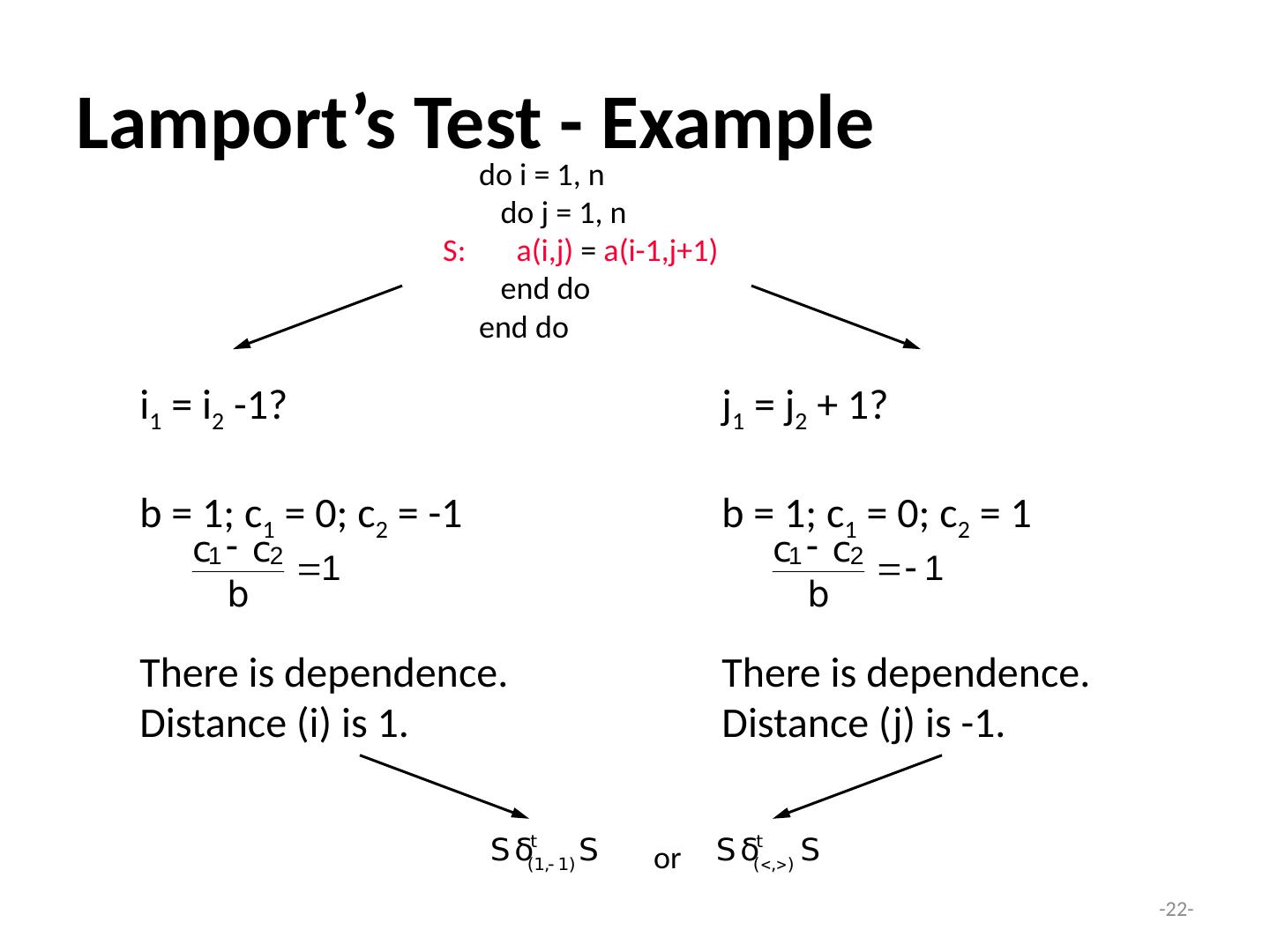
22 .- 22 - Lamport’s Test - Example i 1 = i 2 -1? b = 1; c 1 = 0; c 2 = -1 There is dependence. Distance ( i ) is 1. do i = 1, n do j = 1, n S: a(i,j) = a(i-1,j+1) end do end do j 1 = j 2 + 1? b = 1; c 1 = 0; c 2 = 1 There is dependence. Distance (j) is -1. or

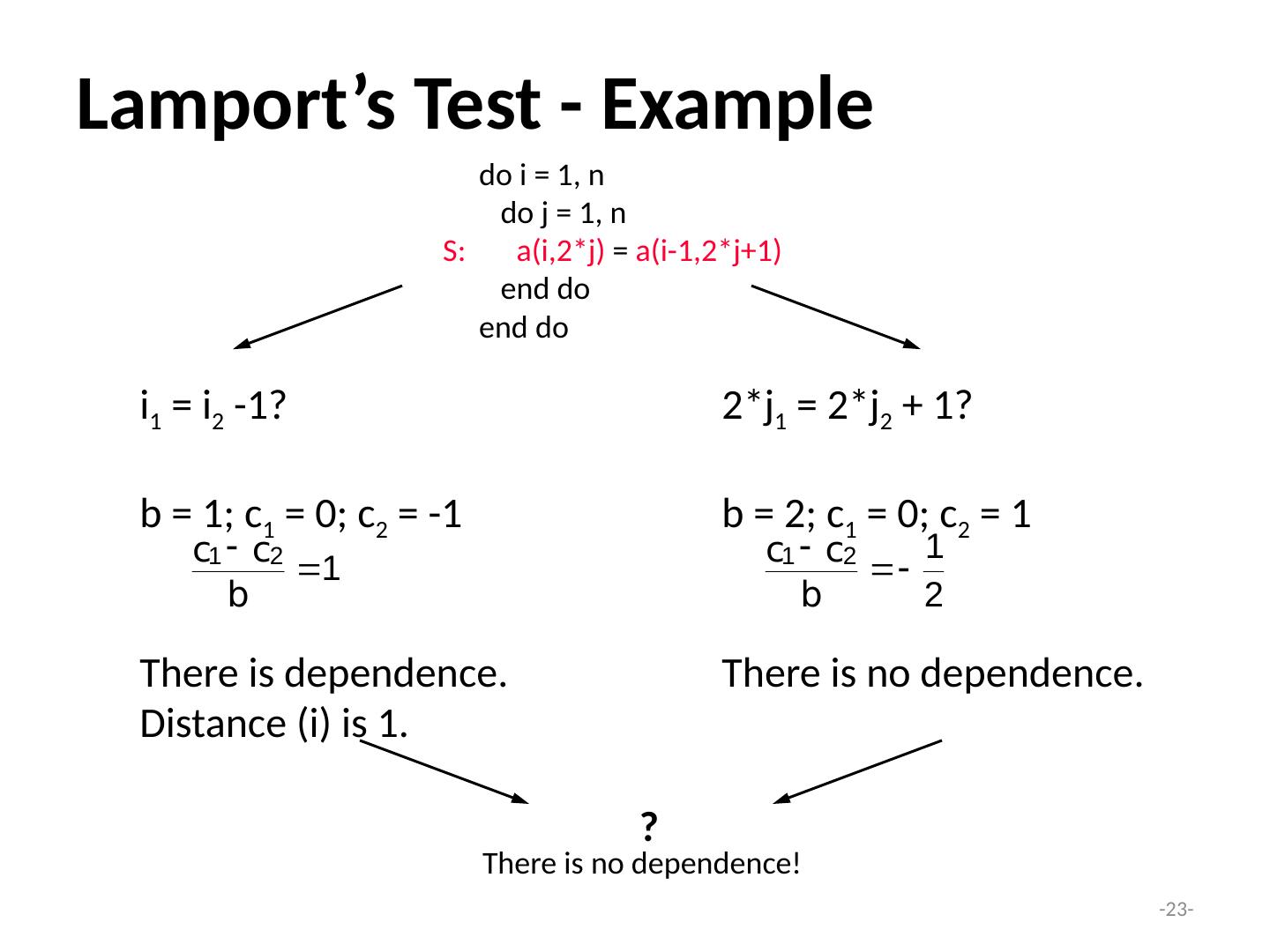
23 .- 23 - Lamport’s Test - Example i 1 = i 2 -1? b = 1; c 1 = 0; c 2 = -1 There is dependence. Distance ( i ) is 1. do i = 1, n do j = 1, n S: a(i,2*j) = a(i-1,2*j+1) end do end do 2*j 1 = 2*j 2 + 1? b = 2; c 1 = 0; c 2 = 1 There is no dependence. ? There is no dependence!

24 .- 24 - GCD Test Given the following equation: an integer solution exists if and only if: Problems: ignores loop bounds. gives no information on distance or direction of dependence. often gcd (……) is 1 which always divides c, resulting in false dependences.

25 .- 25 - GCD Test - Example Does there exist two iteration vectors i 1 and i 2 , such that 1 £ i 1 £ i 2 £ 10 and such that: 2*i 1 = 2*i 2 -1? or 2*i 2 - 2*i 1 = 1? There will be an integer solution if and only if gcd (2,-2) divides 1 . This is not the case, and hence, there is no dependence! do i = 1, 10 S 1 : a(2*i) = b(i) + c(i) S 2 : d(i) = a(2*i-1) end do

26 .- 26 - GCD Test Example Does there exist two iteration vectors i 1 and i 2 , such that 1 £ i 1 £ i 2 £ 10 and such that: i 1 = i 2 -100? or i 2 - i 1 = 100? There will be an integer solution if and only if gcd (1,-1) divides 100 . This is the case, and hence, there is dependence! Or is there? do i = 1, 10 S 1 : a( i ) = b( i ) + c( i ) S 2 : d( i ) = a(i-100) end do

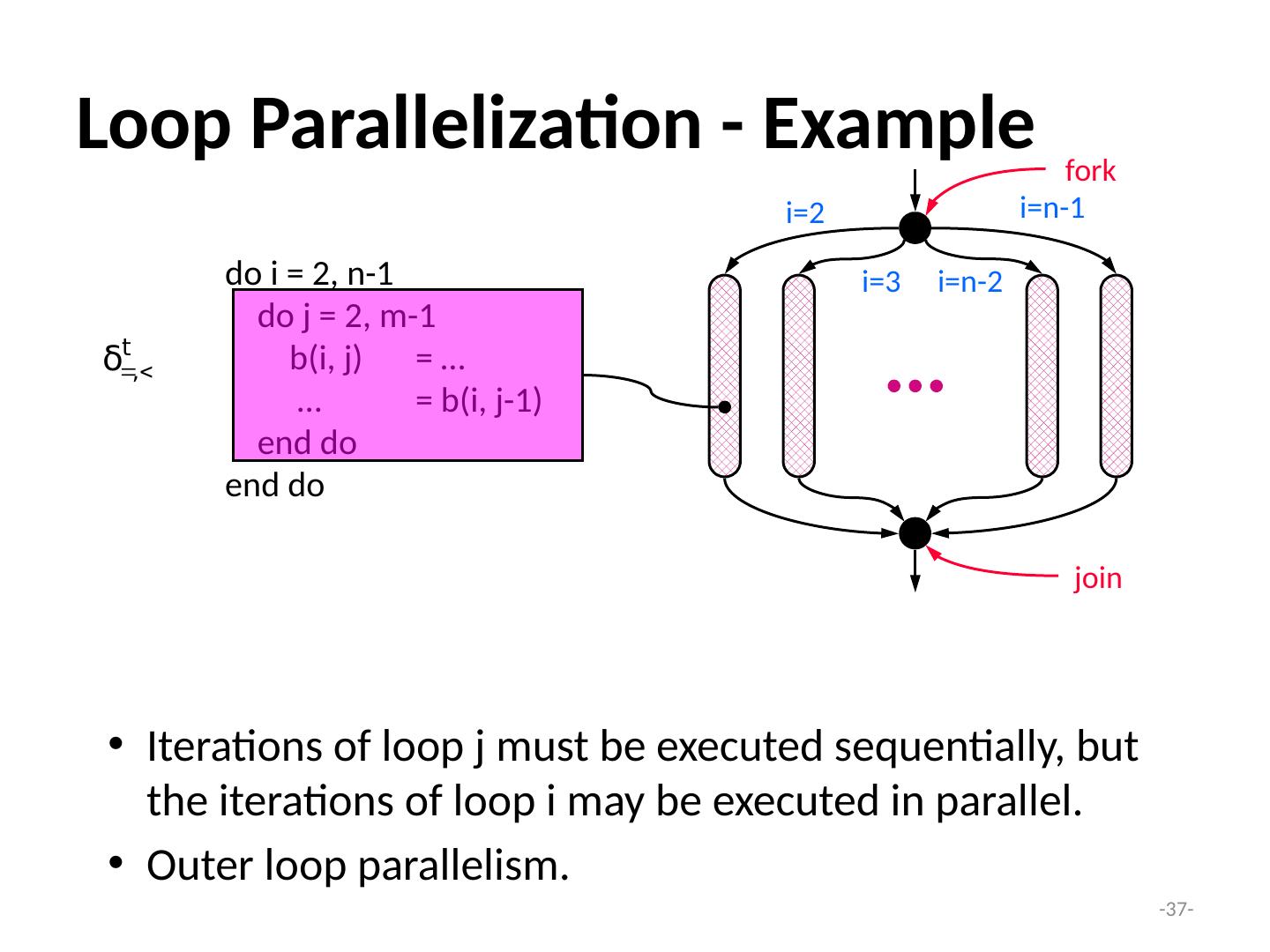
27 .- 27 - Dependence Testing Complications Unknown loop bounds. What is the relationship between N and 10? Triangular loops. Must impose j < i as an additional constraint. do i = 1, N S 1 : a( i ) = a(i+10) end do do i = 1, N do j = 1, i-1 S: a( i,j ) = a( j,i ) end do end do

28 .- 28 - More Complications User variables Same problem as unknown loop bounds, but occur due to some loop transformations (e.g., normalization). do i = 1, 10 S 1 : a( i ) = a( i+k ) end do do i = L, H S 1 : a( i ) = a(i-1) end do do i = 1, H-L S 1 : a( i+L ) = a(i+L-1) end do ß

29 .- 29 - More Complications: Scalars do i = 1, N S 1 : x = a(i) S 2 : b(i) = x end do do i = 1, N S 1 : x(i) = a(i) S 2 : b(i) = x(i) end do j = N-1 do i = 1, N S 1 : a(i) = a(j) S 2 : j = j - 1 end do do i = 1, N S 1 : a(i) = a(N-i) end do sum = 0 do i = 1, N S 1 : sum = sum + a(i) end do do i = 1, N S 1 : sum(i) = a(i) end do sum += sum(i) i = 1, N Þ Þ Þ