Inside Spirit X3

1 .Inside Spirit X3 Redesigning Boost.Spirit for C++11 Joel de Guzman Ciere Consulting

2 .Agenda Quick Overview Parser Combinator Let’s Build a Toy Spirit X3 Walk-through Spirit X3

3 .What’s Spirit A object oriented, recursive-descent parser and output generation library for C++ Implemented using template meta-programming techniques Syntax of Parsing Expression Grammars (PEGs) directly in C++, used for input and output format specification Target grammars written entirely in C++ No separate tools to compile grammar Seamless integration with other C++ code Immediately executable

4 .Spirit X3 Experimental C++11 Hackable , simpler design Minimal code base and dependencies MPL Fusion Phoenix? Proto? Better error handling Faster compile times c alc4.cpp example SpiritX3 : TOTAL : 4.27 secs Spirit2 : TOTAL : 10.00 secs

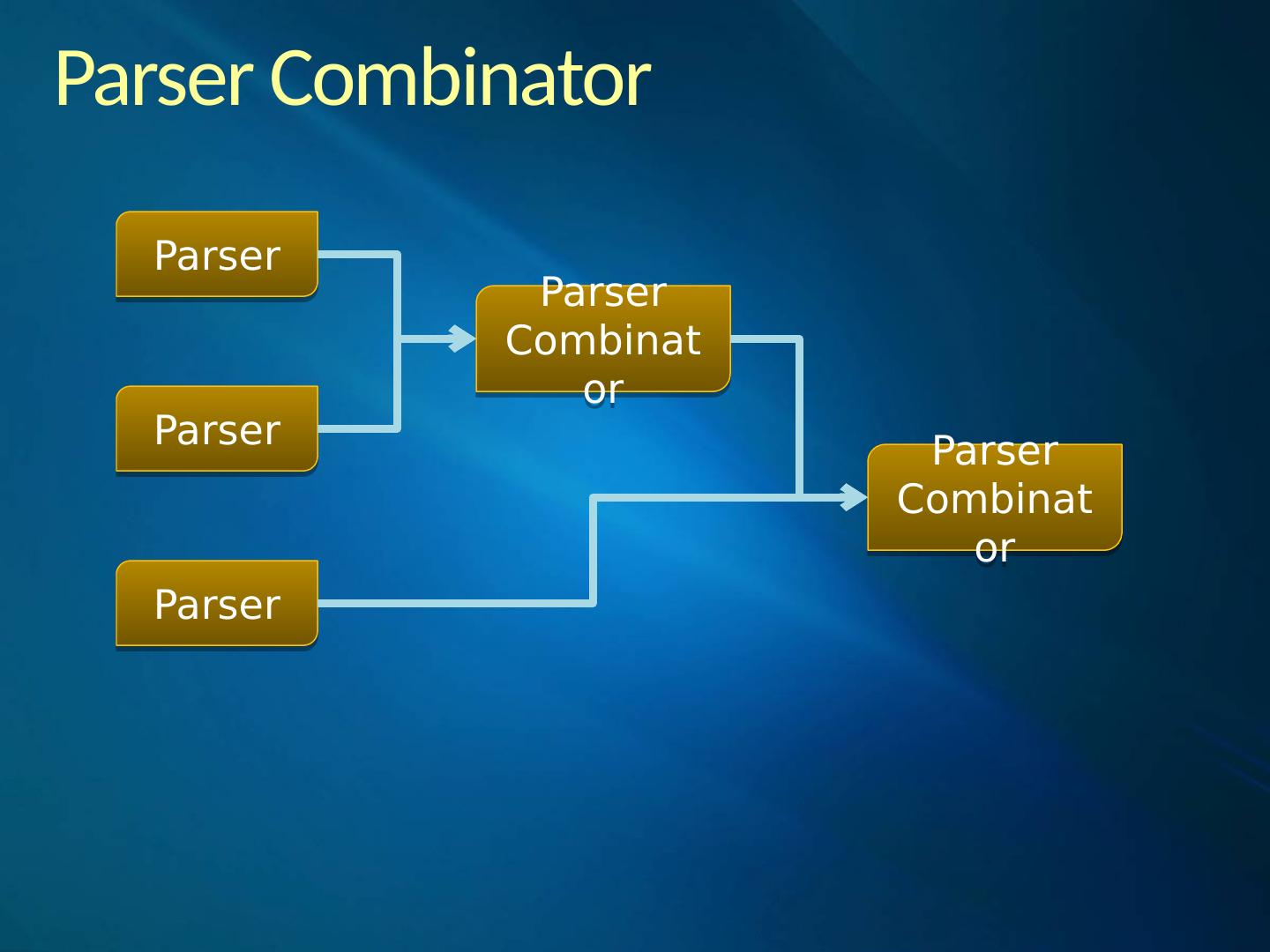
5 .Parser Combinator A Parser is a function A character parser A numeric parser Parsers can be composed to form higher order parser functions E.g. a sequence parser accepts two parsers and returns a composite parser Such a higher order parser function is called a Parser Combinator . A Parser Combinator accepts several parsers as input and returns a composite parser as result

6 .Parser Combinator Parser Parser Parser Combinator Parser Parser Combinator

7 .Parser Combinator Primitives (plain characters , uint_ , etc.) bool match_char (char ch ) { return ch == input(); } Sequences bool match_sequence (F1 f1 , F2 f2 ) { return f1() && f2(); } Alternatives bool match_alternative (F1 f1 , F2 f2 ) { return f1() || f2(); } Modifiers ( kleen , plus, etc.) bool match_kleene (F f ) { while (f()); return true; } Nonterminals (factor, term, expr ) bool match_rule () { return match_rhs (); }

8 .Parsing Expression Grammar Formal grammar for describing a formal language in terms of a set of rules used to recognize strings of this language Does not require a tokenization stage Similar to Extended Backus-Naur Form (EBNF) Unlike (E)BNF, PEG’s are not ambiguous Exactly one valid parse tree for each PEG Any PEG can be directly represented as a recursive-descent parser Different Interpretation as EBNF Greedy Loops First come first serve alternates

9 .Parsing Expression Grammar Formal grammar for describing a formal language in terms of a set of rules used to recognize strings of this language Does not require a tokenization stage Similar to Extended Backus-Naur Form (EBNF) Unlike (E)BNF, PEG’s are not ambiguous Exactly one valid parse tree for each PEG Any PEG can be directly represented as a recursive-descent parser Different Interpretation as EBNF Greedy Loops First come first serve alternates

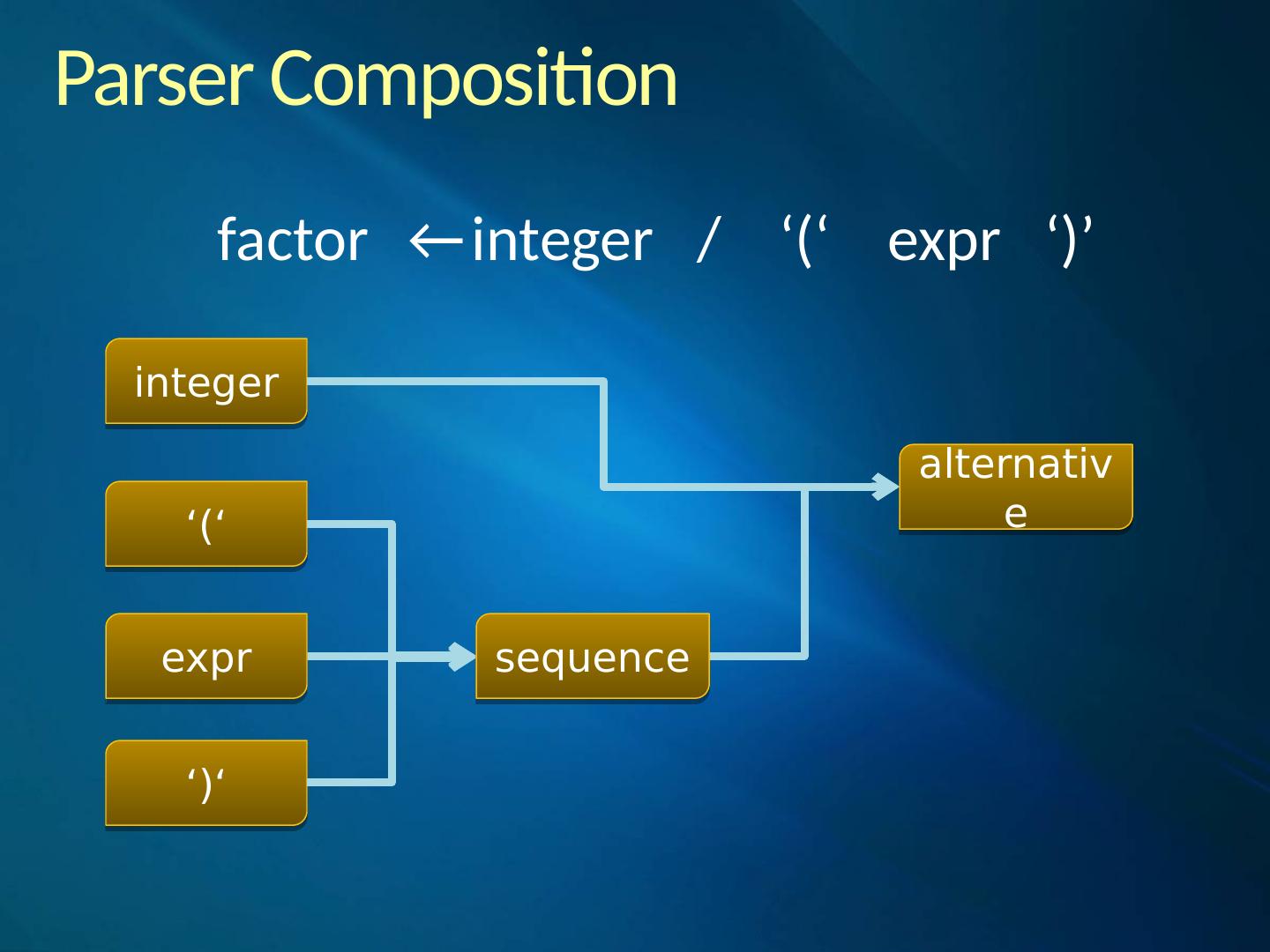
10 .Parser Composition integer ‘(‘ ‘)‘ factor ← integer / ‘(‘ expr ‘)’ expr alternative sequence

11 .Parser Composition factor ← integer / ‘(‘ expr ‘)’ bool match_fact () { return match_integer () || ( match_char ( ‘(‘ ) && match_expr () && match_char ( ‘)’ ) ); }

12 .Let’s build a toy Spirit X3

13 .The Parser B ase C lass namespace boost { namespace spirit { namespace x3 { template < typename Derived> struct parser { Derived const& derived() const { return * static_cast <Derived const*>(this); } }; }

14 .The parse member function template < typename Iterator , typename Context> bool parse( Iterator & first, Iterator last, Context const& ctx ) const

15 .Postconditions Upon return from p.parse the following post conditions should hold: On a successful match, first is positioned one past the last matching character. On a failed match, first is restored to its original position prior to entry. No post-skips: trailing skip characters will not be skipped.

16 .Our F irst Primitive Parser template < typename Char> struct char_parser : parser< char_parser <Char>> { char_parser (Char ch ) : ch ( ch ) {} template < typename Iterator , typename Context> bool parse( Iterator & first, Iterator last, Context const& ctx ) const { if (first != last && *first == ch ) { ++first; return true; } return false; } Char ch ; };

17 .char_ ET template < typename Char> inline char_parser <Char> char_(Char ch ) { return char_parser <Char>( ch ); };

18 .Our F irst Composite Parser template < typename Left, typename Right> struct sequence_parser : parser< sequence_parser <Left, Right>> { sequence_parser (Left left , Right right ) : left(left), right(right) {} template < typename Iterator , typename Context> bool parse( Iterator & first, Iterator last, Context const& ctx ) const { return left.parse (first, last, ctx ) && right.parse (first, last, ctx ); } Left left ; Right right ; };

19 .Sequence ET template < typename Left, typename Right> inline sequence_parser <Left, Right> operator>>( parser<Left> const& left, parser<Right> const& right) { return sequence_parser <Left, Right>( left.derived (), right.derived ()); }

20 .Another Composite Parser template < typename Left, typename Right> struct alternative_parser : parser< alternative_parser <Left, Right>> { alternative_parser (Left left , Right right ) : left(left), right(right) {} template < typename Iterator , typename Context> bool parse( Iterator & first, Iterator last, Context const& ctx ) const { if ( left.parse (first, last, ctx )) return true; return right.parse (first, last, ctx ); } Left left ; Right right ; };

21 .Alternative ET template < typename Left, typename Right> inline alternative_parser <Left, Right> operator|( parser<Left> const& left, parser<Right> const& right) { return alternative_parser <Left, Right>( left.derived (), right.derived ()); }

22 .Simple Rules auto abc = char_(‘a’) >> char_(‘b’) >> char_(‘c’) ; auto a_or_bc = char_(‘a’) | ( char_(‘b’) >> char_(‘c’) ) ;

23 .But how about Recursion? I want a rule that parses these inputs: “x” “ax” “ aax ” “ aaaaax ” In other words: I want zero or more ‘ a’s followed by an ‘x’ No, we don’t have the Kleene star yet ;-)

24 .But how about Recursion? auto const x = char_(‘x’) | ax; auto const ax = char_(‘a’) >> x;

25 .But how about Recursion? auto const x = char_(‘x’) | ax ; auto const ax = char_(‘a’) >> x ; Oooops !

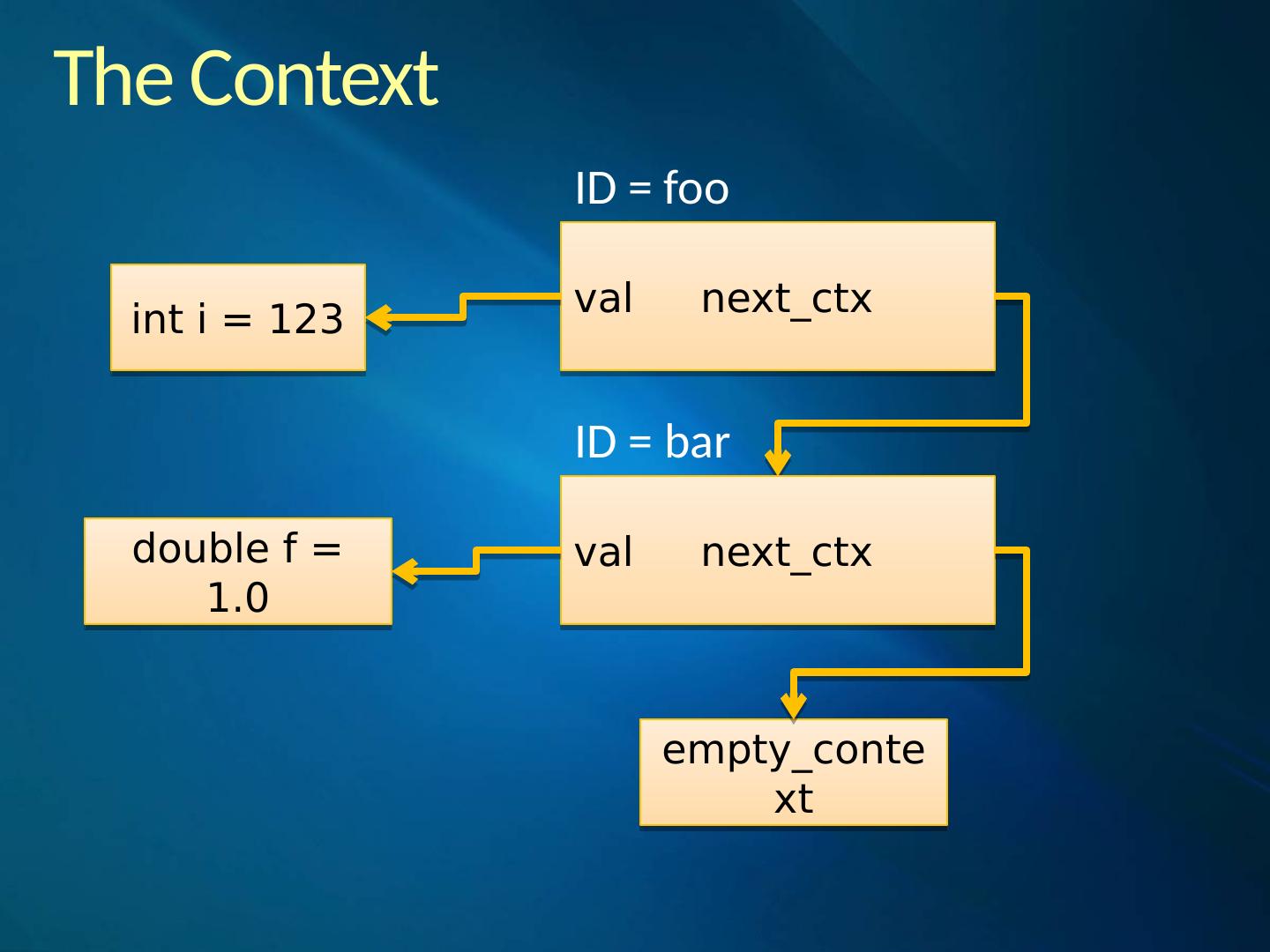
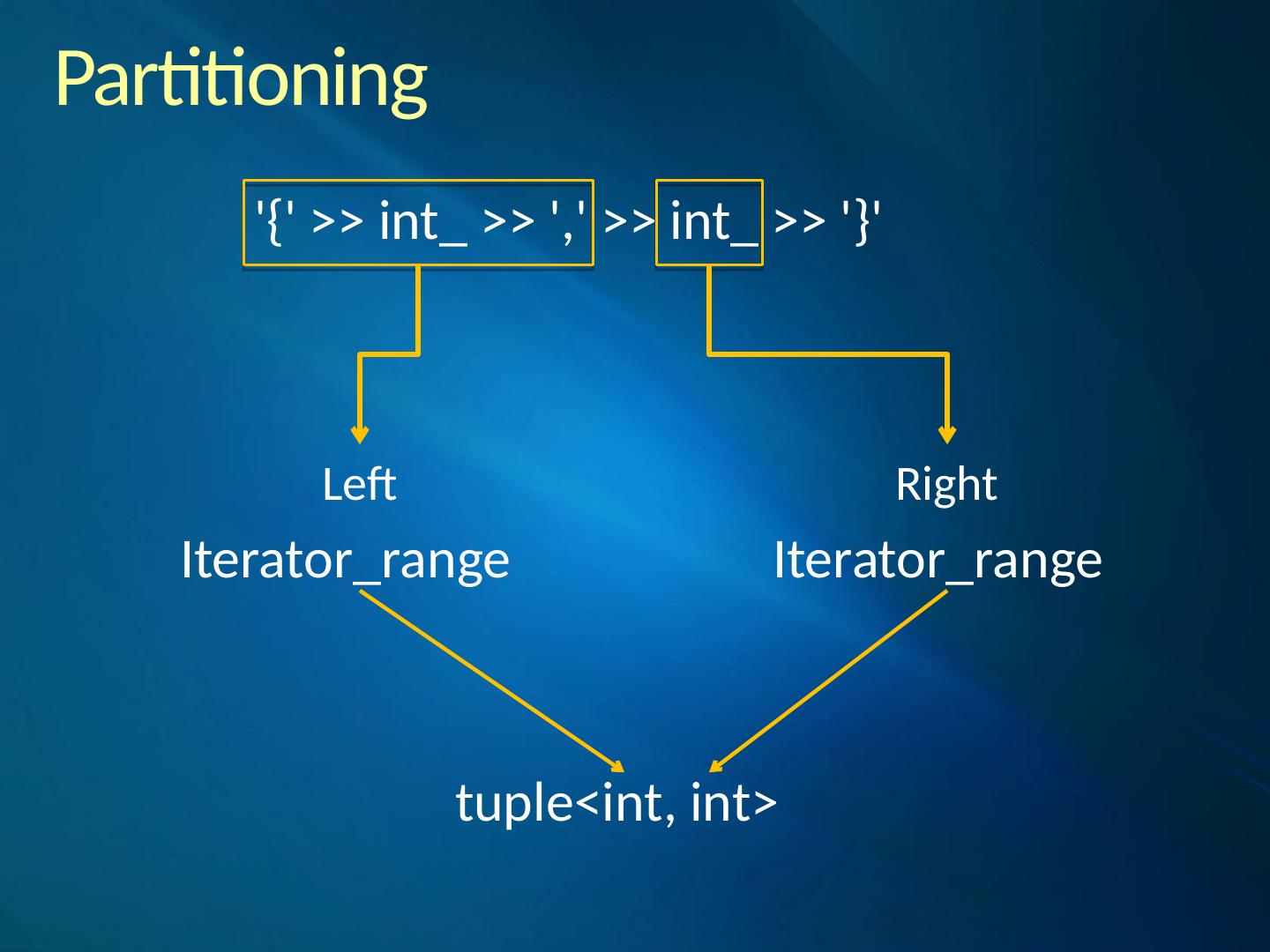
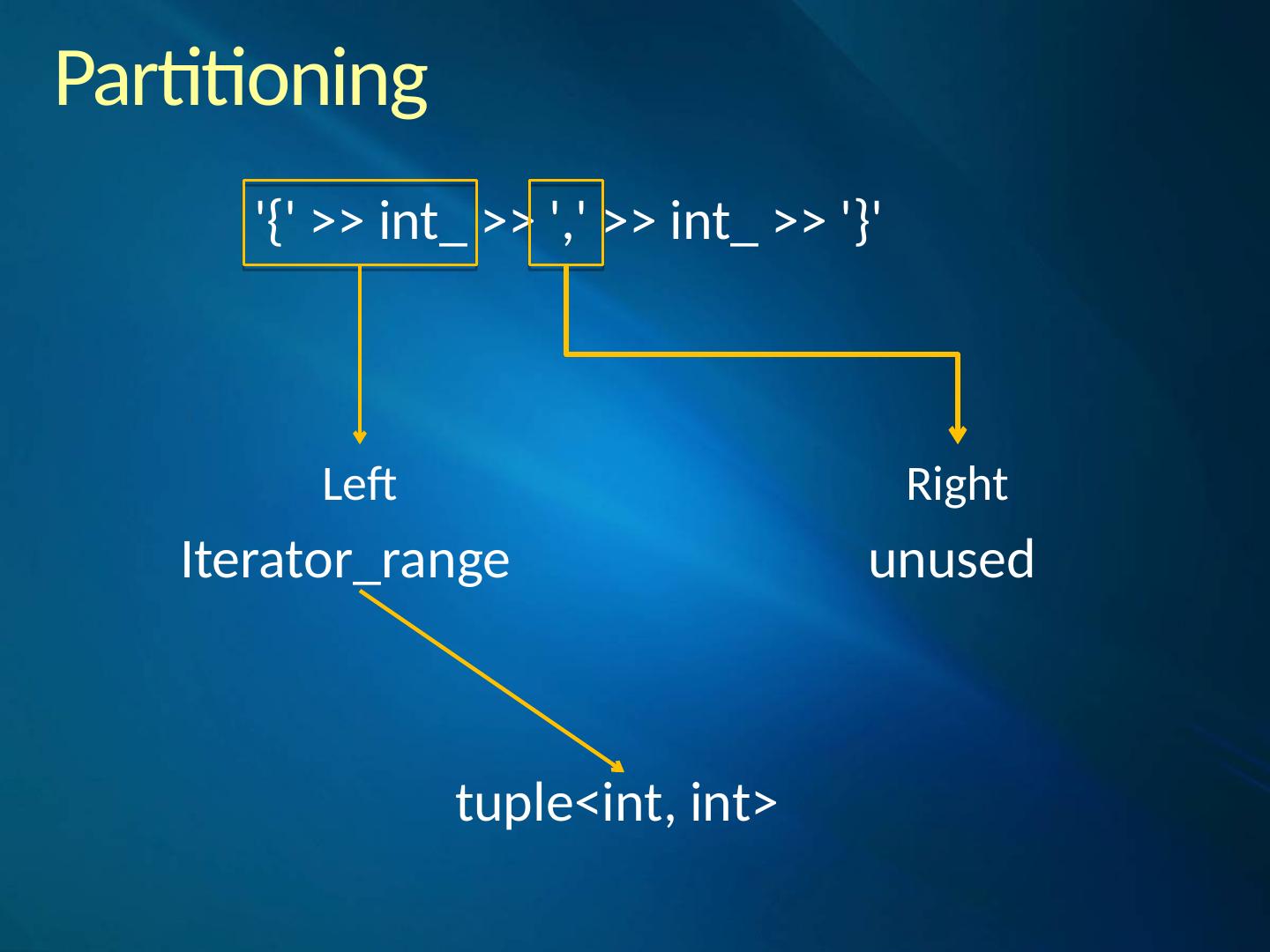
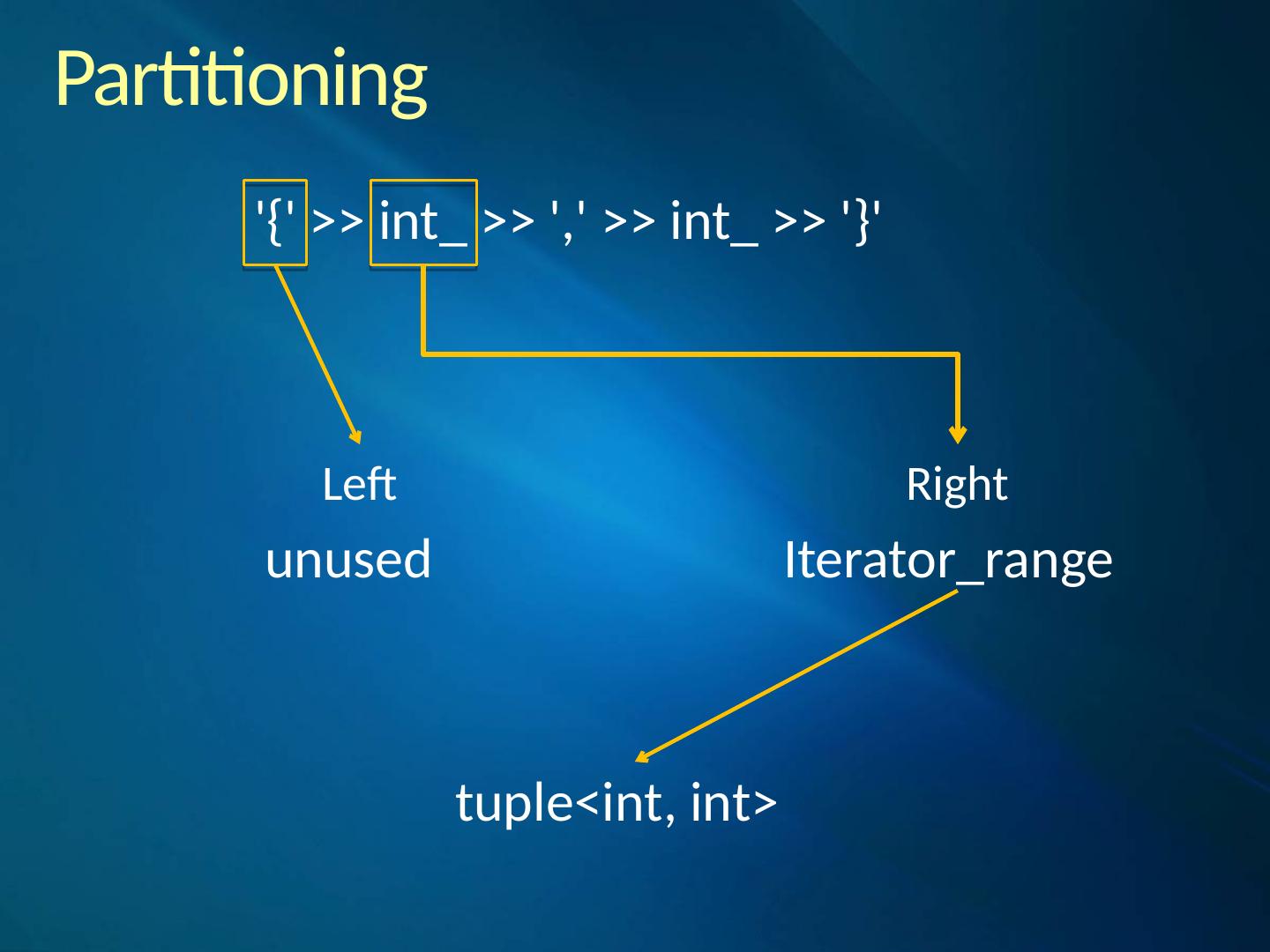
26 .Nonterminals The rule is a polymorphic parser that acts as a named placeholder capturing the behavior of a PEG expression assigned to it. Naming a PEG expression allows it to be referenced later and makes it possible for the rule to call itself. This is one of the most important mechanisms and the reason behind the word “recursive” in recursive descent parsing.

27 .Spirit-2 and Spirit-Classic style Uses type-erasure Abstract class with virtual functions Boost or std function rule< Iterator > x, ax; x = char_(‘x’) | ax; ax = char_(‘a’) >> x;

28 .Problems with type-erasure All template parameters for parse should be known before hand. Hence the rule needs to know the “scanner” type (Spirit-Classic) and the Iterator type (Spirit-2). Code bloat The virtual functions force instantiations even if, in the end, they are not really used. Same with Boost or std function. Prevents optimizations The virtual function is an opaque wall. In general, compilers cannot see beyond this opaque wall and cannot perform optimizations.

29 .X3 style Does not use type-erasure Inspired by Spirit-Classic Subrules Taken to the next level with the help of C++11 facilities that were not available at the time (e.g. auto and variadic templates) V2 and Classic subrules are compile time monsters with its heavy reliance on expression templates