傅里叶光学

1 .工程光学 郭 峰 青岛理工大学 Engineering Optics

2 . 课程特点与要求 教师与课程的基本要求： 　　 传授知识，掌握方法 教师与课程的高级要求： 　　 开启心智，拓展视野 教师与课程的理想要求 /38 我讲授的目的，不是为你们参加考试做准备－－甚至不是为你们服务于工业或军事做准备，我最想做的是向你们给出对这个奇妙世界的一些欣赏，以及物理学家们看待这个世界的方式，这是现今时代里真正文化的主要部分 费曼

3 .　卷积运算 　相关运算 　 傅里叶变换 　 傅里叶光学 /57

4 ./57 1 ．卷积的定义 卷积的定义式： 一 卷积运算 二维卷积的表达式：

5 ./57 卷积表示两个函数乘积的积分，但与通常的两个函数乘积的积分不同，在积分式中有 ，则其意义为： a. 置换变量 ：将 与 中的自变量 x 换成积分变量 ， 如下图 0 1 1 0 1 一 卷积运算

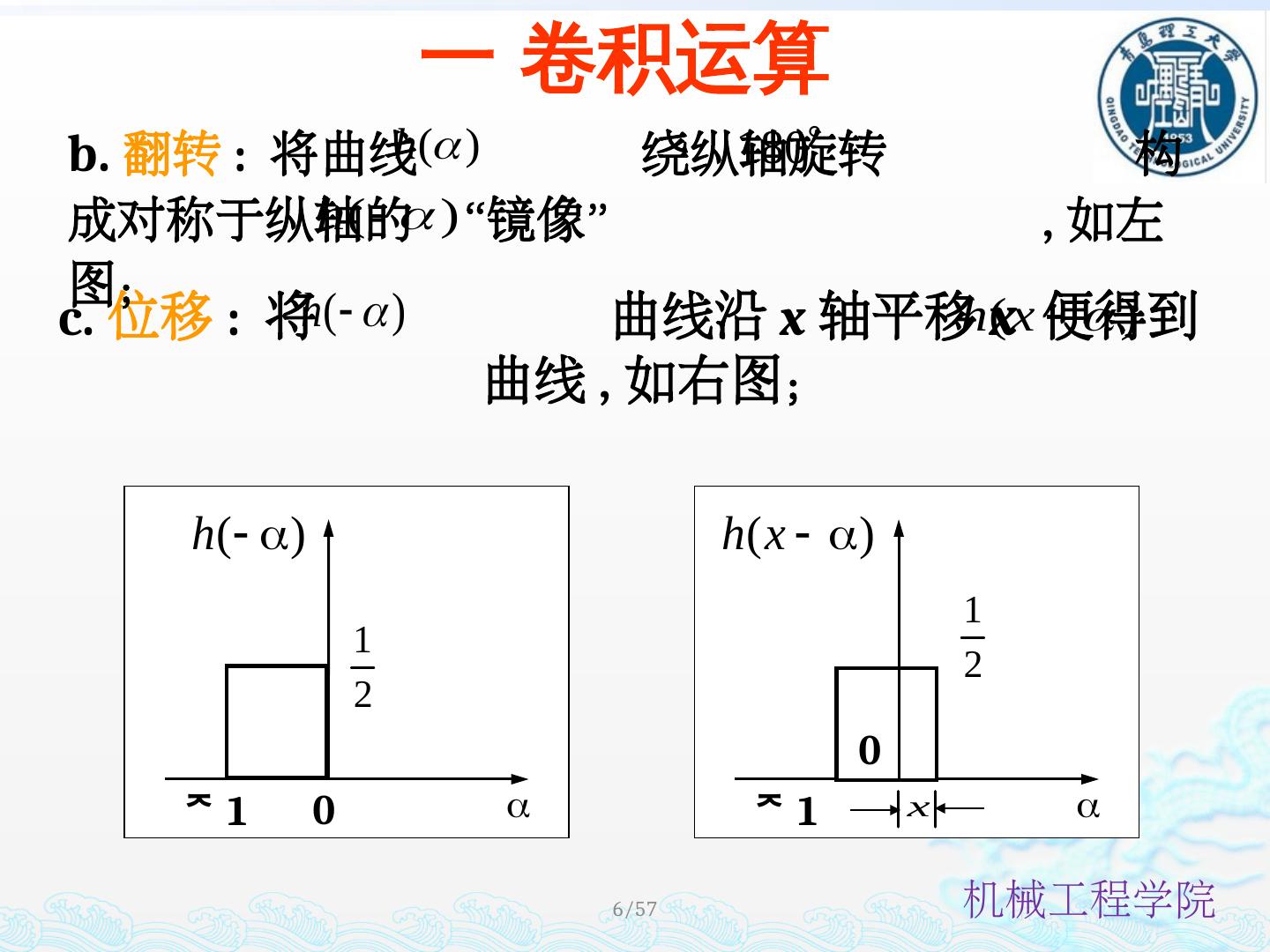
6 ./57 c. 位移 : 将 曲线沿 x 轴平移 x 便得到 曲线 , 如右图； b. 翻转 : 将曲线 绕纵轴旋转 构成对称于纵轴的 “镜像” , 如左图； 0  1 0  1 一 卷积运算

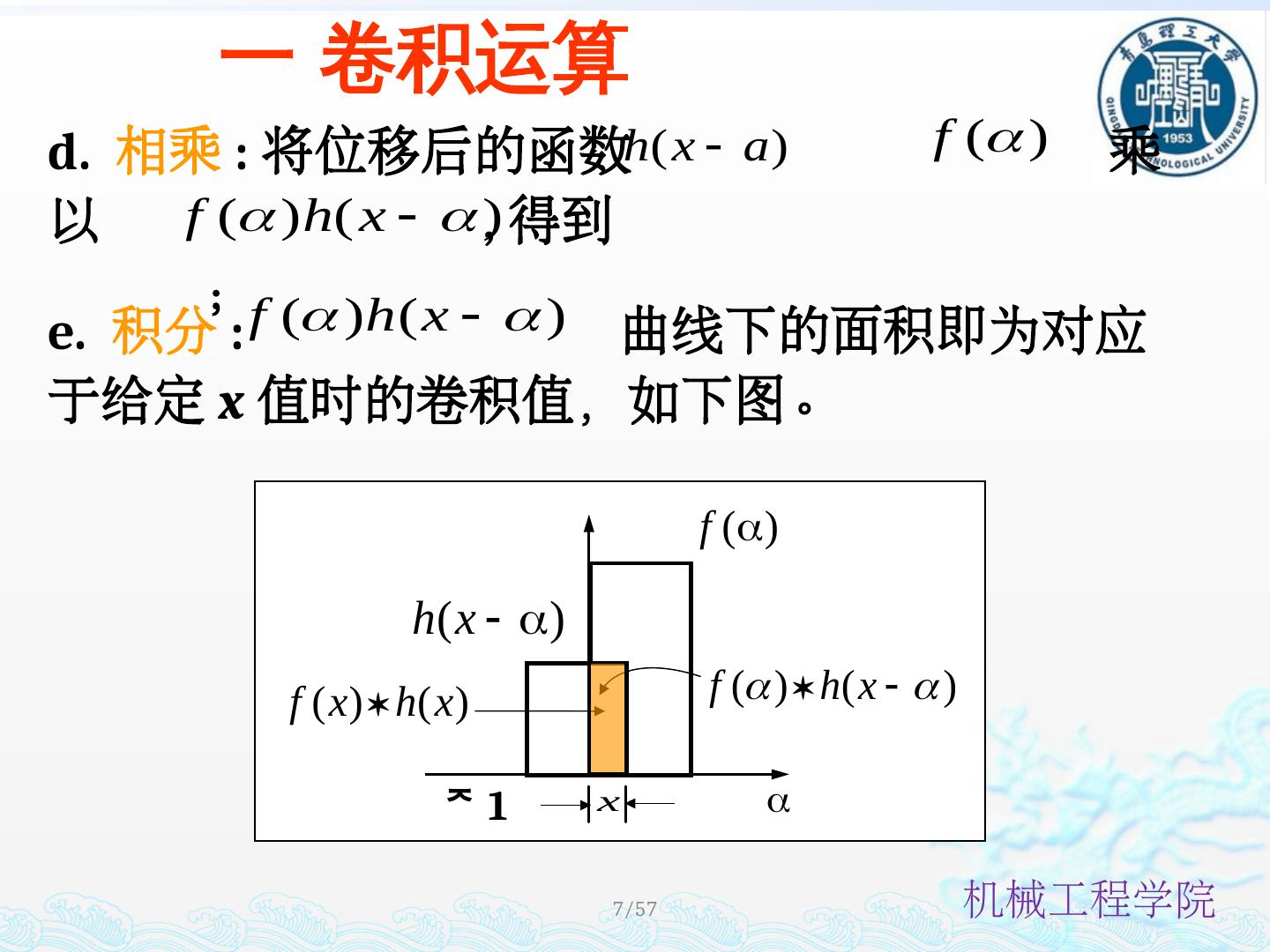
7 ./57 d. 相乘 : 将位移后的函数 乘以 , 得到 ； e. 积分 : 曲线下的面积即为对应于给定 x 值时的卷积值，如下图。 0  1 一 卷积运算

8 .卷积的功能就是将函数进行模糊处理 展宽：卷积运算结果的宽度是被卷积函数的宽度之和 平滑：被卷积的函数经过卷积运算，其细微结构被消除，函数本身的起伏振荡变得平缓圆滑 /57 一 卷积运算

9 .2 ．卷积的性质 1) 　交换性 2) 　线性 　　同样 /57 一卷 积运算

10 .一 卷积运算 3) 　位移不变性 若 则 /57

11 .一 卷积运算 /57

12 .一 卷积运算 /57

13 ./57 0 1 -1 x f(x)*h(x) - 2

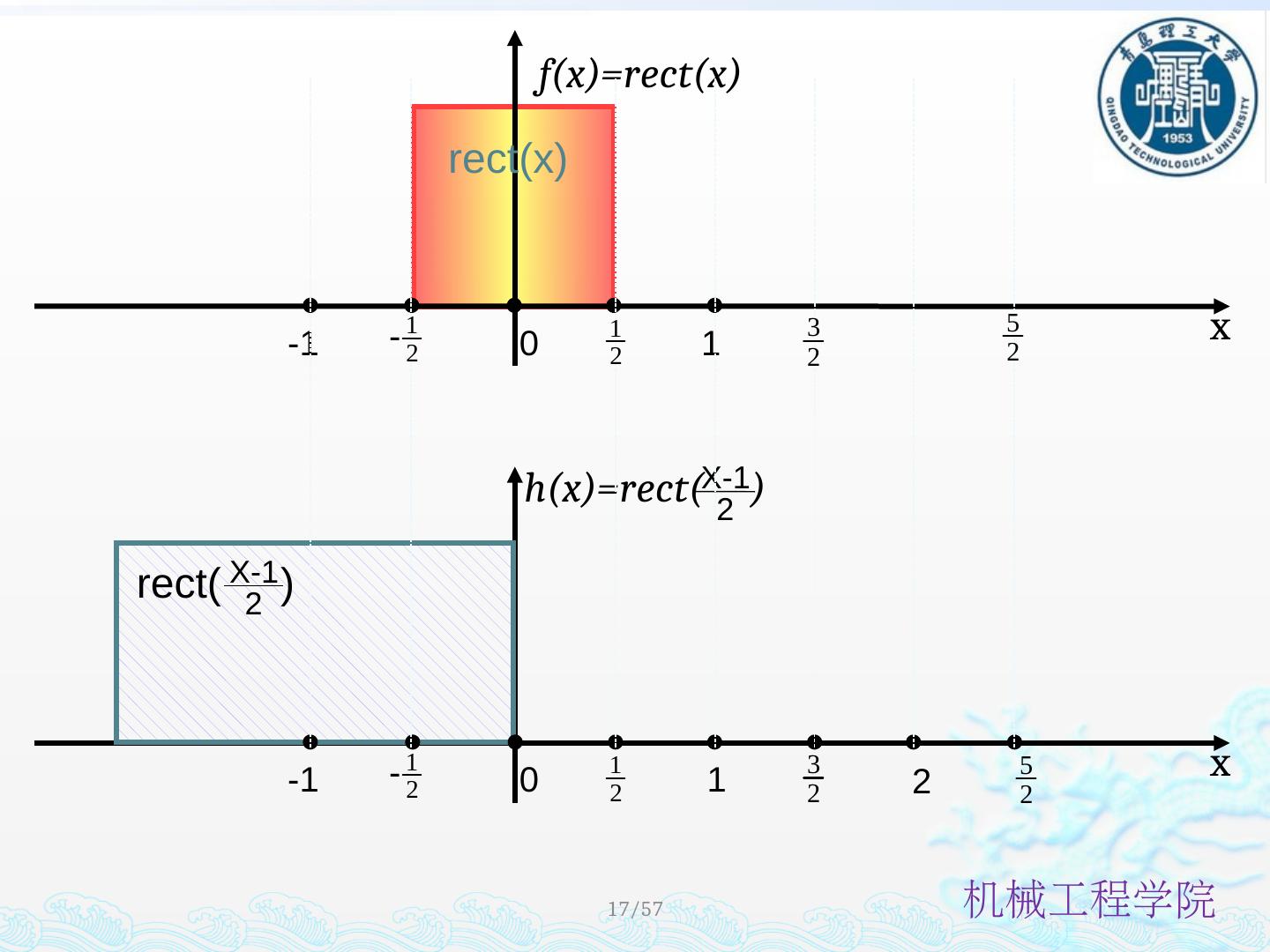
14 ./57 x f(x)=rect(x) rect(x) 0 1 -1 - x h(x)=rect( ) 0 1 -1 - rect( ) X-1 2 2 X-1 2

15 ./57 x h(x)=rect( ) 0 1 -1 - 2 X-1 2 0 1 -1 x h(x)*f(x) - f(x)=rect(x) 2

16 ./57 x h(x)=rect( ) 0 1 -1 - 2 X-1 2 0 1 -1 x h(x)*f(x) - f(x)=rect(x) 2

17 ./57 x h(x)=rect( ) 0 1 -1 - 2 X-1 2 0 1 -1 x h(x)*f(x) - f(x)=rect(x) 2

18 ./57 h(x)=rect( ) X-1 2 x 0 1 -1 - 2 0 1 -1 x f(x)*h(x) - f(x)=rect(x) 2

19 ./57 5 ．卷积计算 2) 已知： 求： 解：

20 ./57 因此有

21 ./57 0  2 2

22 .二 相关运算 1 相关运算的定义 互相关 /57 平移、扫描、求和 自相关

23 .二 相关运算 互相关是函数间相似性的量度 　　两个完全不同的、毫无关系的函数 　互相关的值是零 　　两个函数在某一部位上存在相似性 　 存在非零的互相关值在相应的位置 自相关是函数自身相似性的量度 　　零点的自相关值最大 　　函数自身的复制性决定自相关值 /57 问题：为什么卷积和相关的运算差别并不大，但物理意义却差这么多？

24 .

25 .统计学 中，加权的 滑动平均 是一种卷积。  概率论 中，两个统计独立变量 X 与 Y 的和的 概率密度函数 是 X 与 Y 的概率密度函数的卷积。   声学 中， 回声 可以用 源声 与一个反映各种 反射效应 的函数的卷积表示。  电子工程 与 信号处理 中，任一个 线性系统 的输出都可以通过将输入信号与系统函数（系统的 冲激响应 ）做卷积获得。  物理学 中，任何一个线性系统（符合 叠加原理 ）都存在卷积。

26 ./114 傅里叶的两个最主要的贡献 —— “ 周期信号都可表示为成谐波关系的正弦信号的加权和” —— 傅里叶的第一个主要论点 “非周期信号都可表示为正弦信号的加权积分” —— 傅里叶的第二个主要论点 三傅里叶变换

27 ./114 将函数表示为不同频率函数的线性组合 　从信号分析的角度 　　 将信号表示为不同频率正（余）弦分量的线性组合 　　信号间进行比较 、分析、处理 　从系统分析角度 　　 通过单频正弦信号激励下的响应，可求得总响应 三傅里叶变换

28 .变换是一种运算，不是因果关系 光学现象可以视为傅里叶变换 　　　　从而任一波前可以分解为一系列不同空间频率的平面波前成分的叠加， 　　　　对于周期函数，空间频率的取值是离散的，而非周期函数空间频率是连续的 不论光学系统是否成像，它都可以看成从输入面到输出面的一种光速完成的变换 /114 三傅里叶变换

29 ./114 x g’(x) 0 d 1