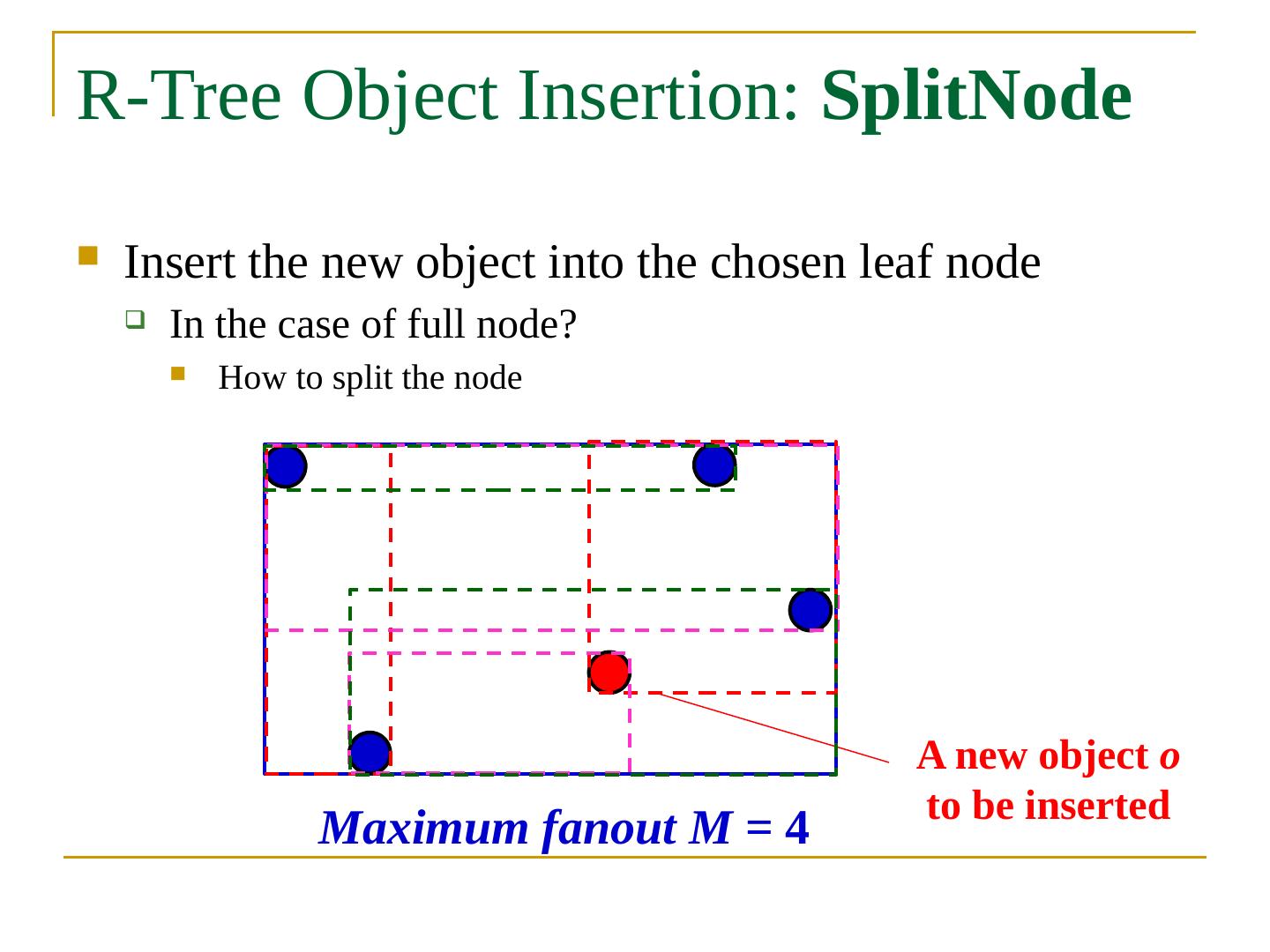
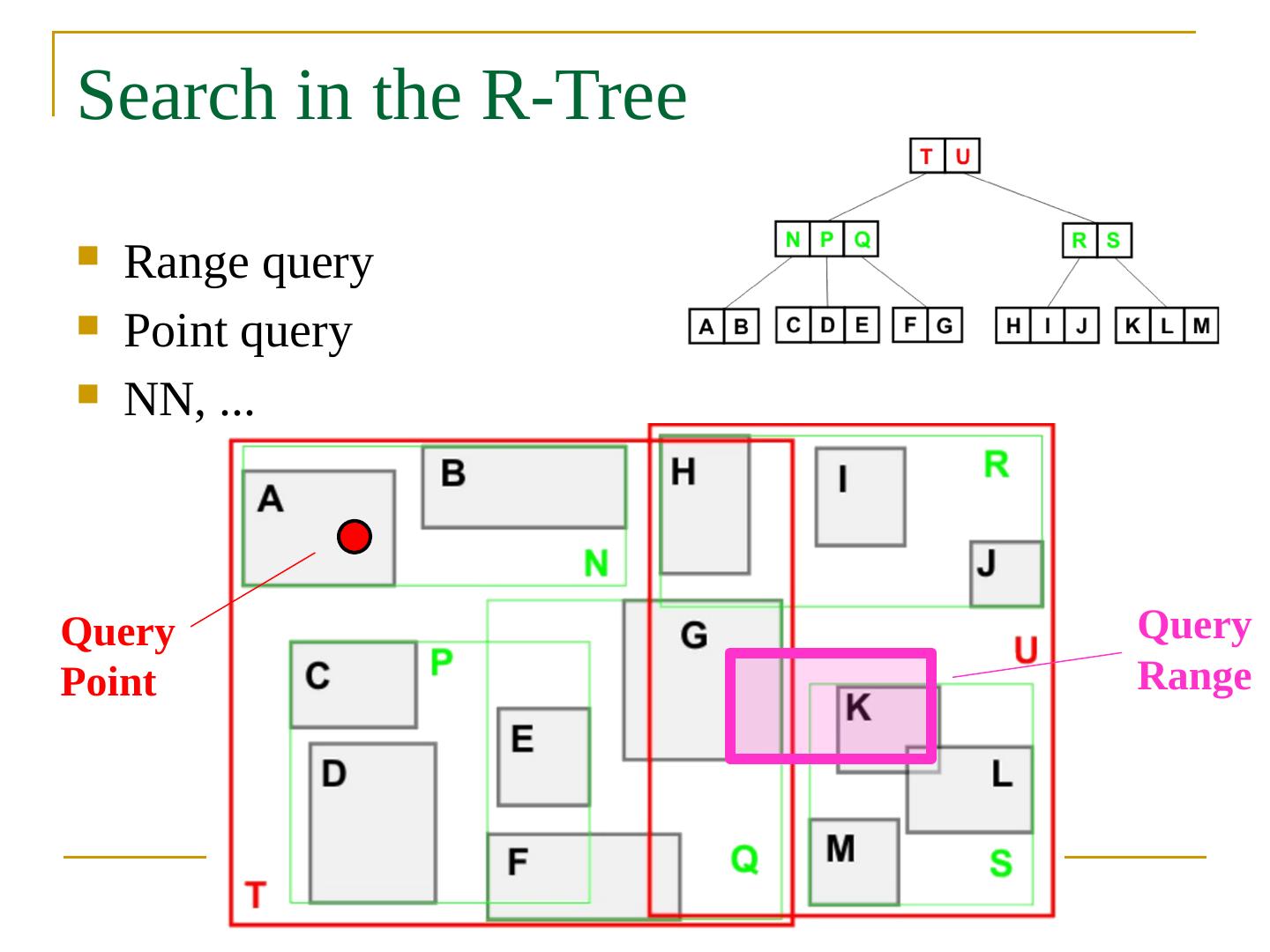
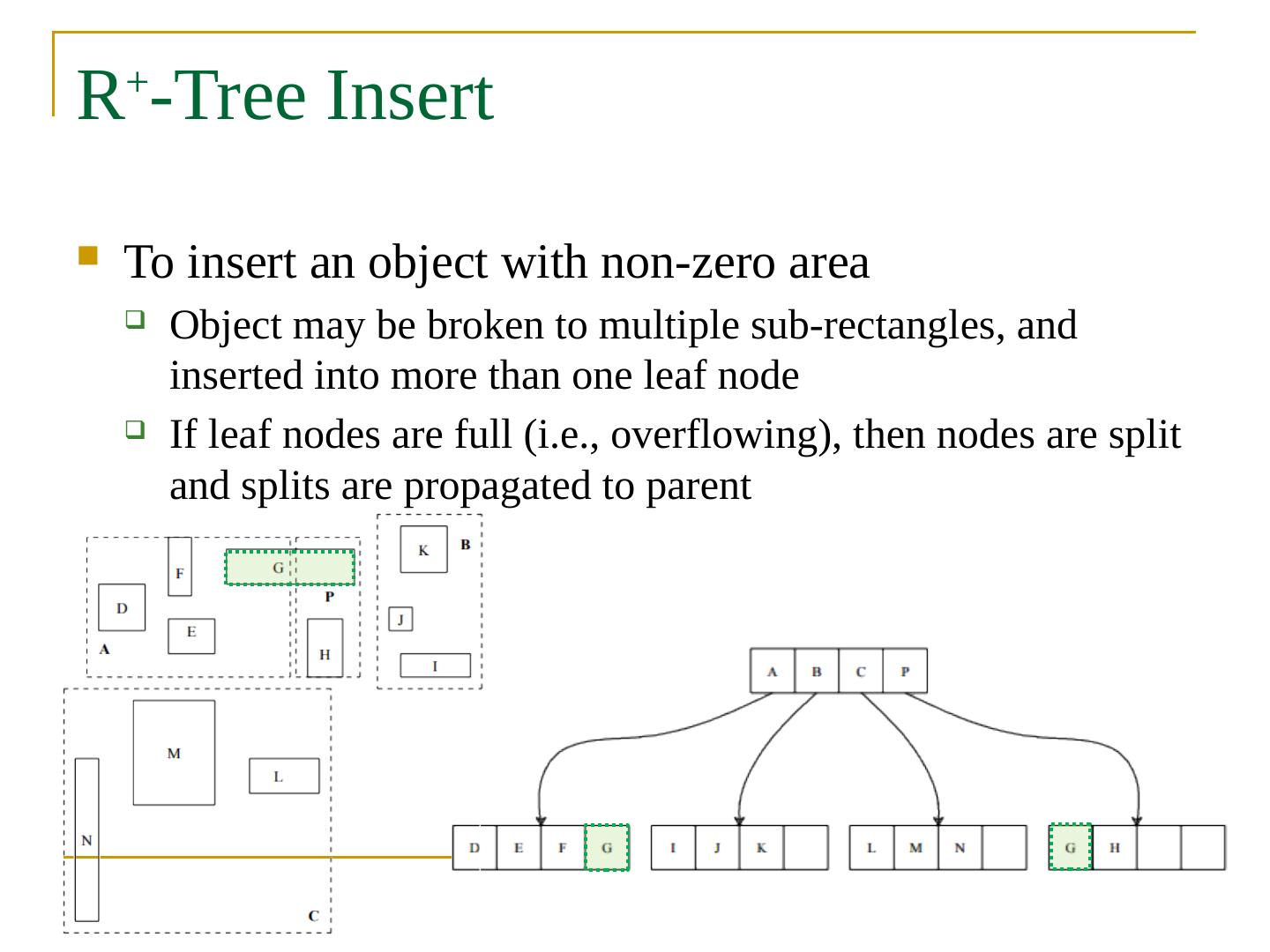
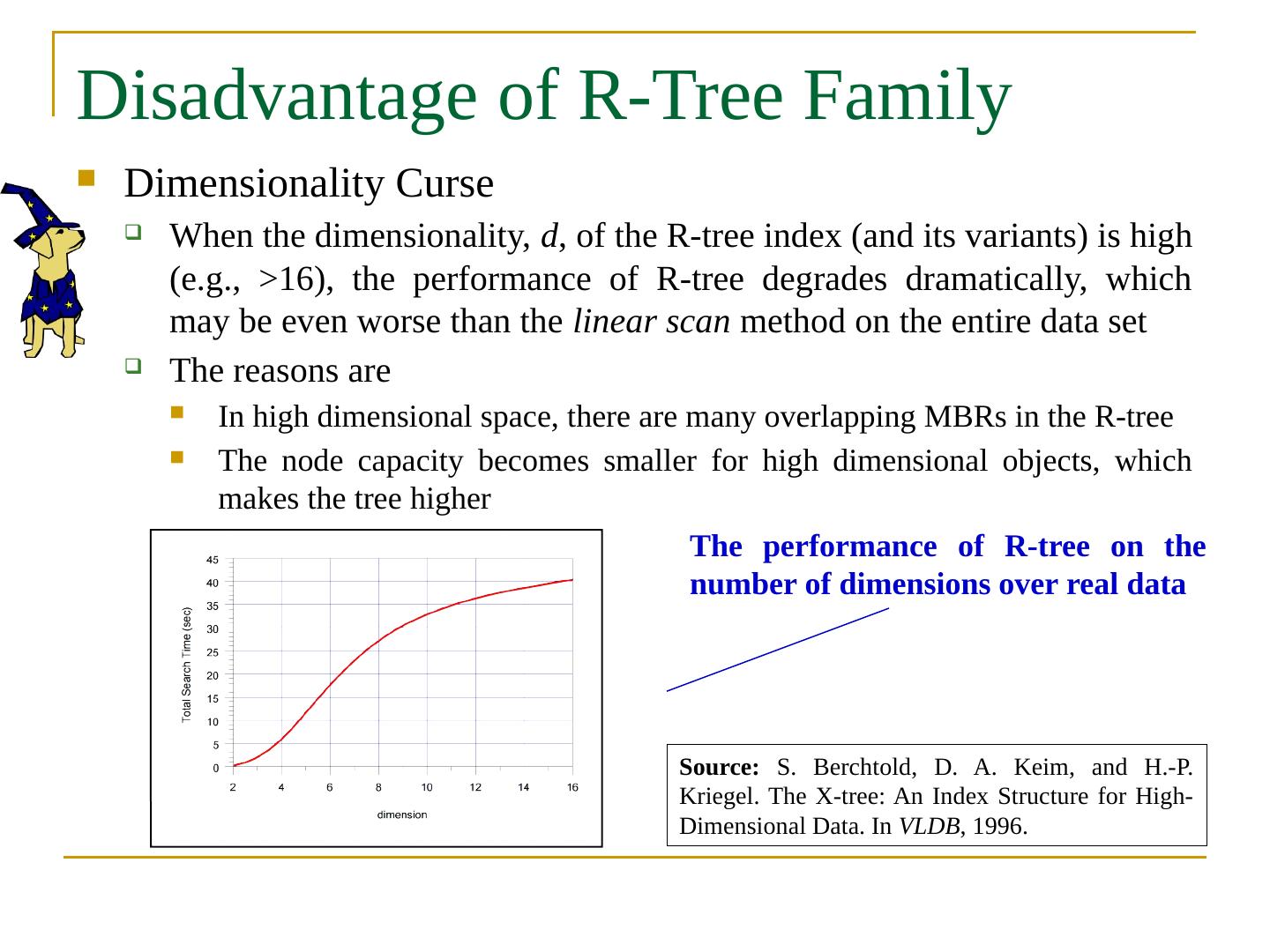
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Indexing Big Data
数据的索引技术,极大提高了数据访问效率,是现代搜索引擎,数据库等产品的核心理论基础,Kent州立大学计算机系教授把常用的数据索引技术进行了分析,并从其中索引到具体的论文研究,方便数据库和搜索引擎技术理论学习者查阅。
Get familiar with many indexing mechanisms:
展开查看详情
1 .Big Data Analytics Xiang Lian Department of Computer Science Kent State University Email: xlian@kent.edu Homepage: http ://www.cs.kent.edu/~xlian/ Indexing Big Data
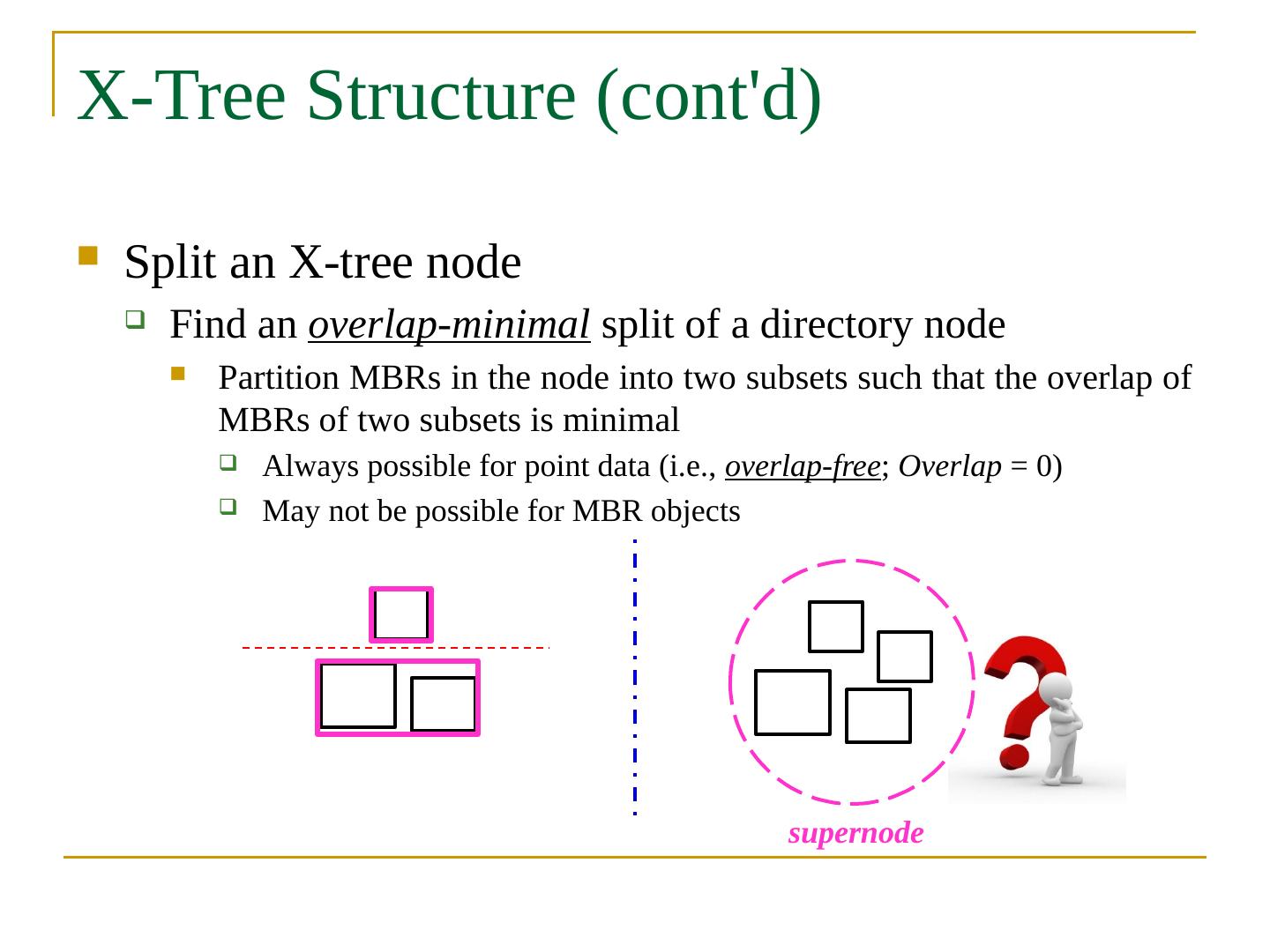
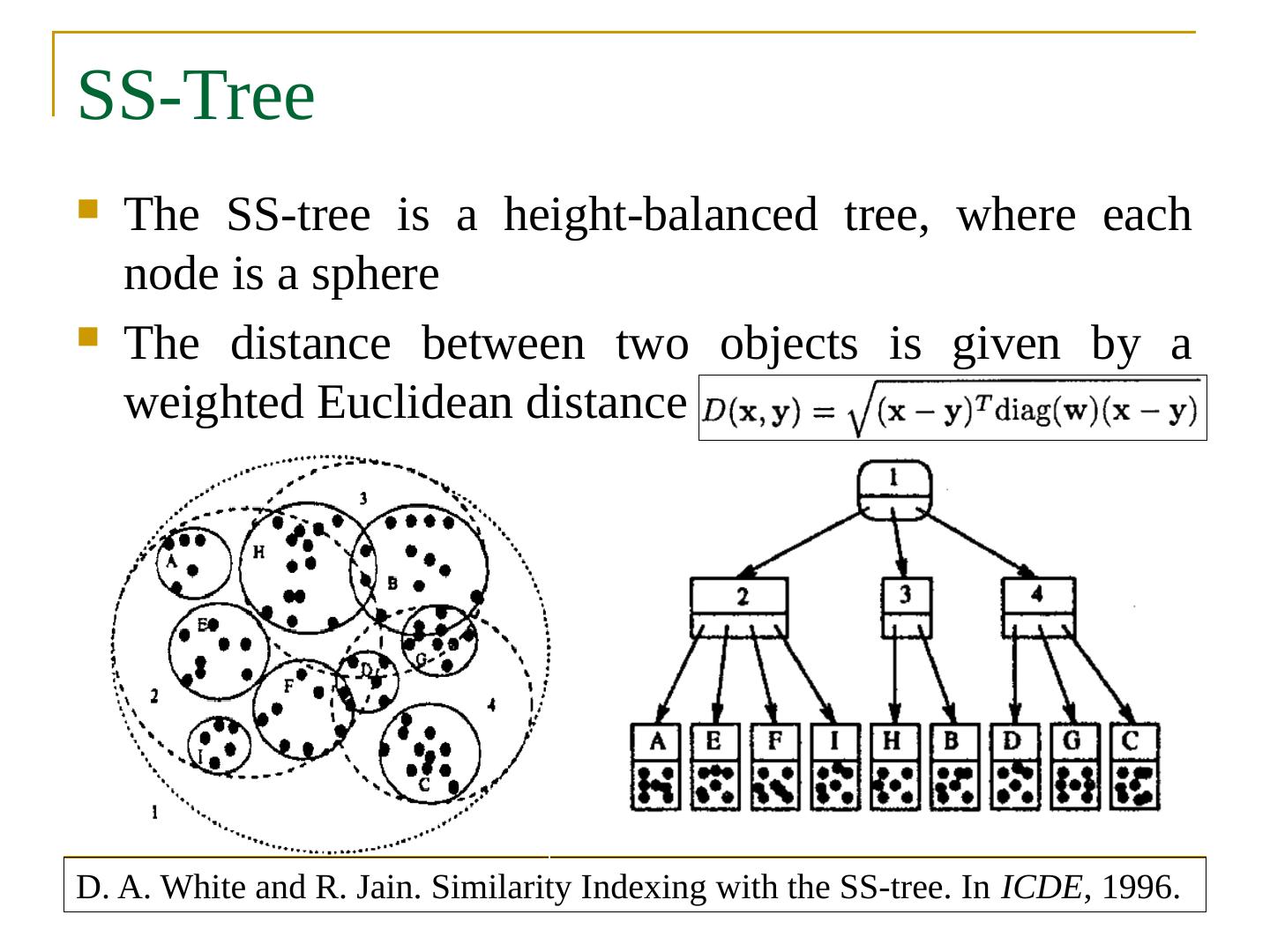
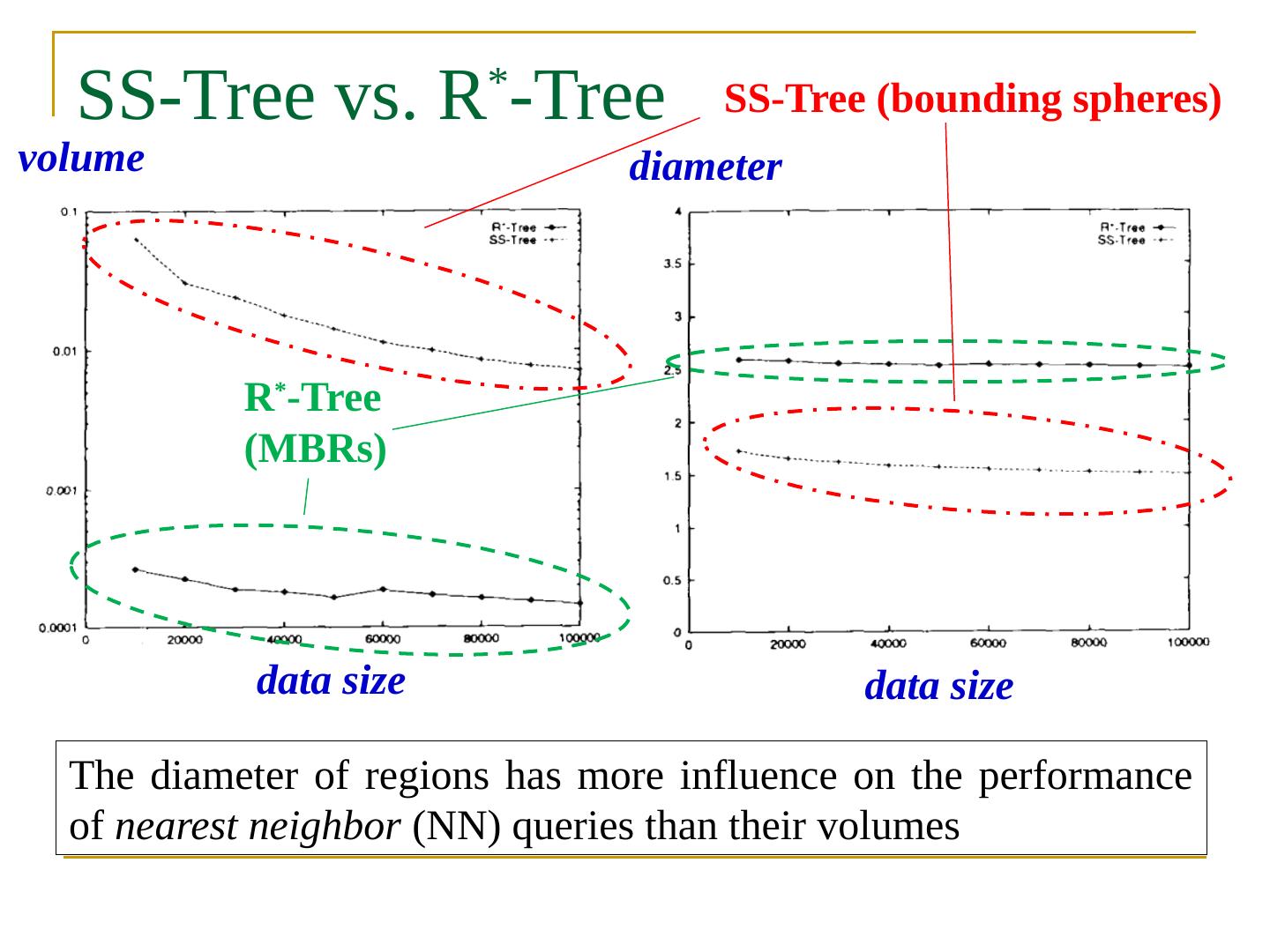
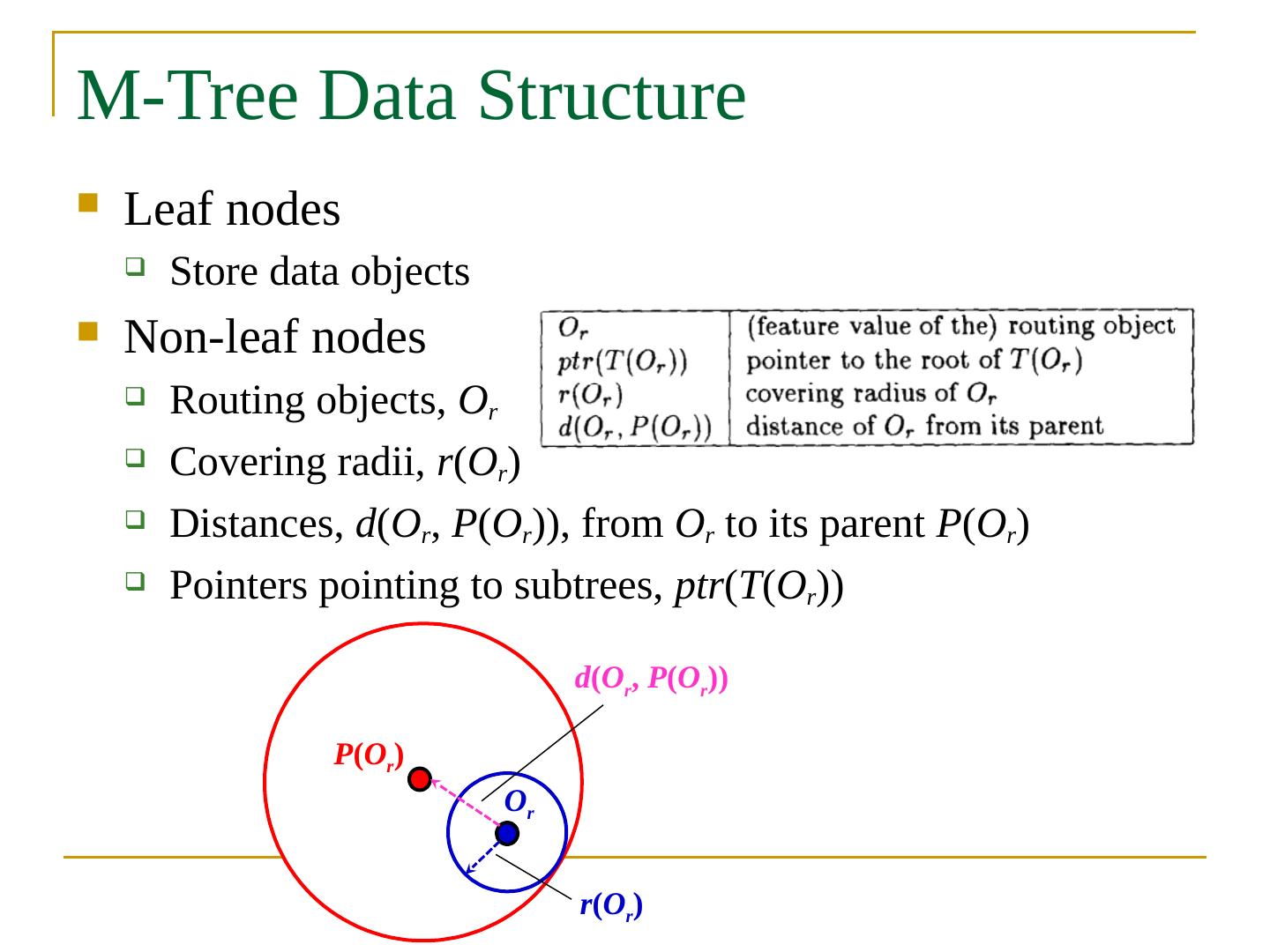
2 .Objectives In this chapter, you will: Get familiar with many indexing mechanisms: B + -tree, extensible hashing, bitmap Grid file Z-order, Hilbert curve Bitmap index Quadtree k -d tree R-tree, R + -tree, R * -tree SS-tree, SR-tree X-tree M-tree Embedding-based index Inverted index Local sensitive hashing Similarity search over indexes Distributed indexes
3 .Outline Introduction Indexing Mechanisms Similarity Search Over Indexes Indexing for High-Dimensional Data Permutation-Based Indexing
4 .Introduction In real applications, we usually collect data of large scale Relational tables with millions of records (tuples) Sensor networks with thousands of sensor nodes, each collecting data such as temperature, humidity, etc. over time In mobile computing or location-based services, millions of mobile users move around in the city … Due to the large scale of data, it is very necessary to build indexes for accelerating the search over large data sets
5 .The Reason for Indexes Consider a relational table with two attributes, PID (person ID) and Age Find those people with age between 20 and 30 Two records : {( PID: 1, Age: 25), (PID: 2, Age: 31)} How about 10 records? 100 records? 1,000 records? 1,000,000 records? The search efficiency is not scalable for large data sets!
6 .The Reason for Indexes Consider a relational table with two attributes, PID (person ID) and Age Find those people with age between 20 and 30 Two records : {( PID: 1, Age: 25), (PID: 2, Age: 31)} How about 10 records? 100 records? 1,000 records? 1,000,000 records? The search efficiency is not scalable for large data sets!
7 .The Reason for Indexes Consider a relational table with two attributes, PID (person ID) and Age Find those people with age between 20 and 30 Two records : {( PID: 1, Age: 25), (PID: 2, Age: 31)} How about 10 records? 100 records? 1,000 records? 1,000,000 records? The search efficiency is not scalable for large data sets!
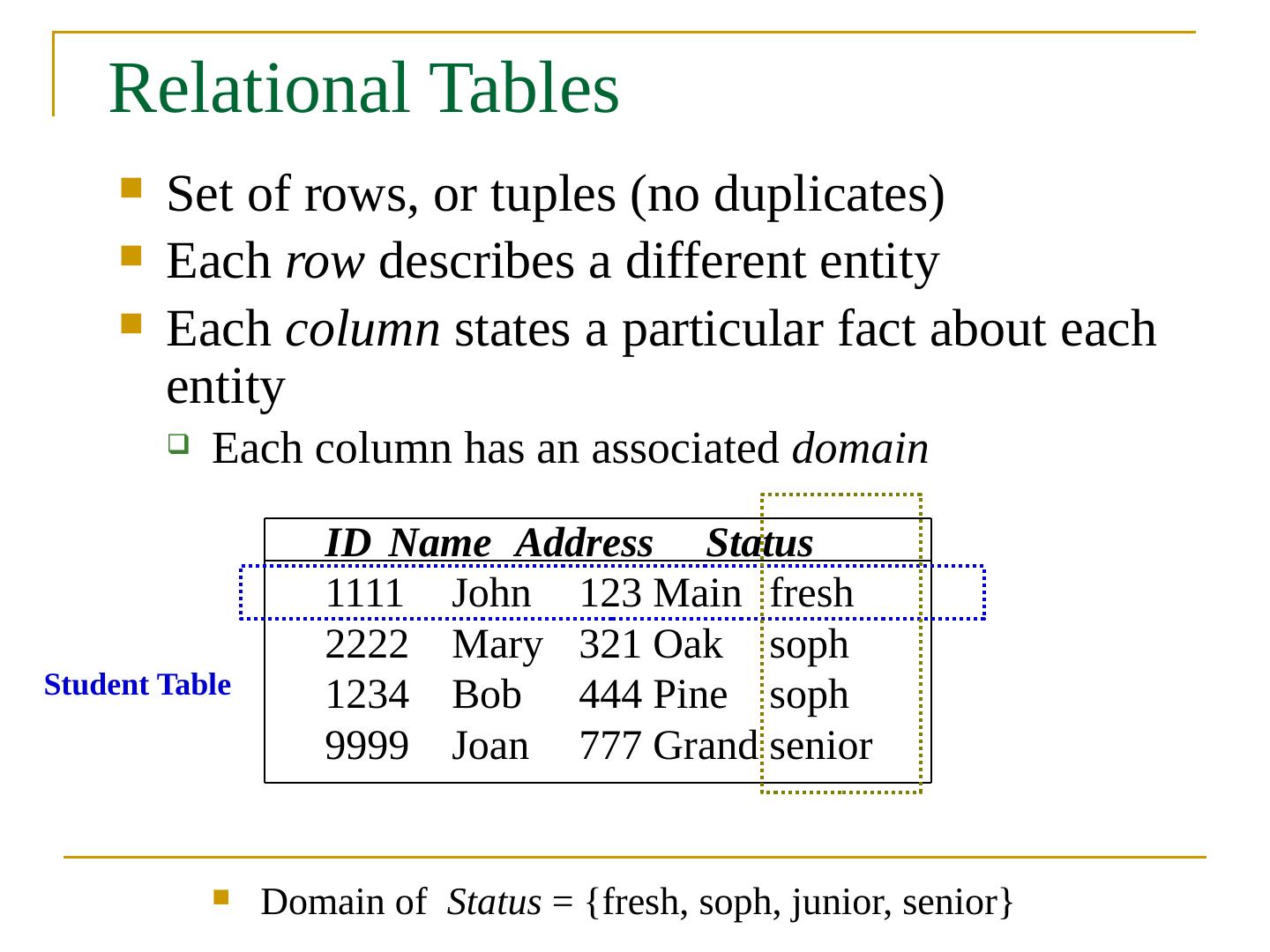
8 .Relational Tables Set of rows, or tuples (no duplicates) Each row describes a different entity Each column states a particular fact about each entity Each column has an associated domain Domain of Status = {fresh, soph , junior, senior} ID Name Address Status 1111 John 123 Main fresh 2222 Mary 321 Oak soph 1234 Bob 444 Pine soph 9999 Joan 777 Grand senior Student Table
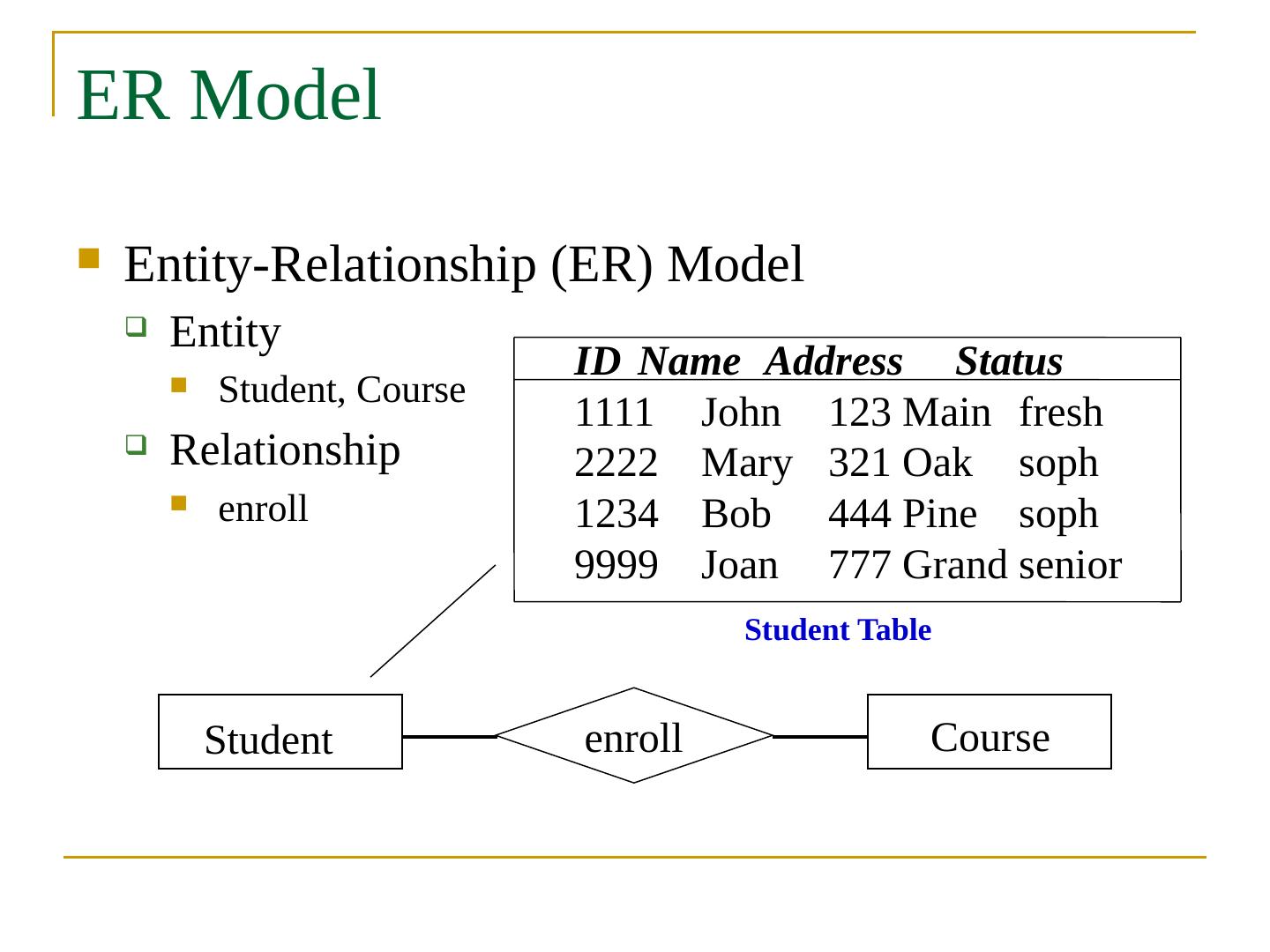
9 .ER Model Entity-Relationship (ER) Model Entity Student, Course Relationship enroll enroll Student Course Student Table ID Name Address Status 1111 John 123 Main fresh 2222 Mary 321 Oak soph 1234 Bob 444 Pine soph 9999 Joan 777 Grand senior
10 .Queries on Relational Tables SQL – database language FROM clause specifies the data source WHERE clause gives the conditions of tuples in the query result SELECT clause retains listed columns SELECT Name FROM Student WHERE Status = ‘ soph ’ and ID >1000 and ID<2000 equality query range query
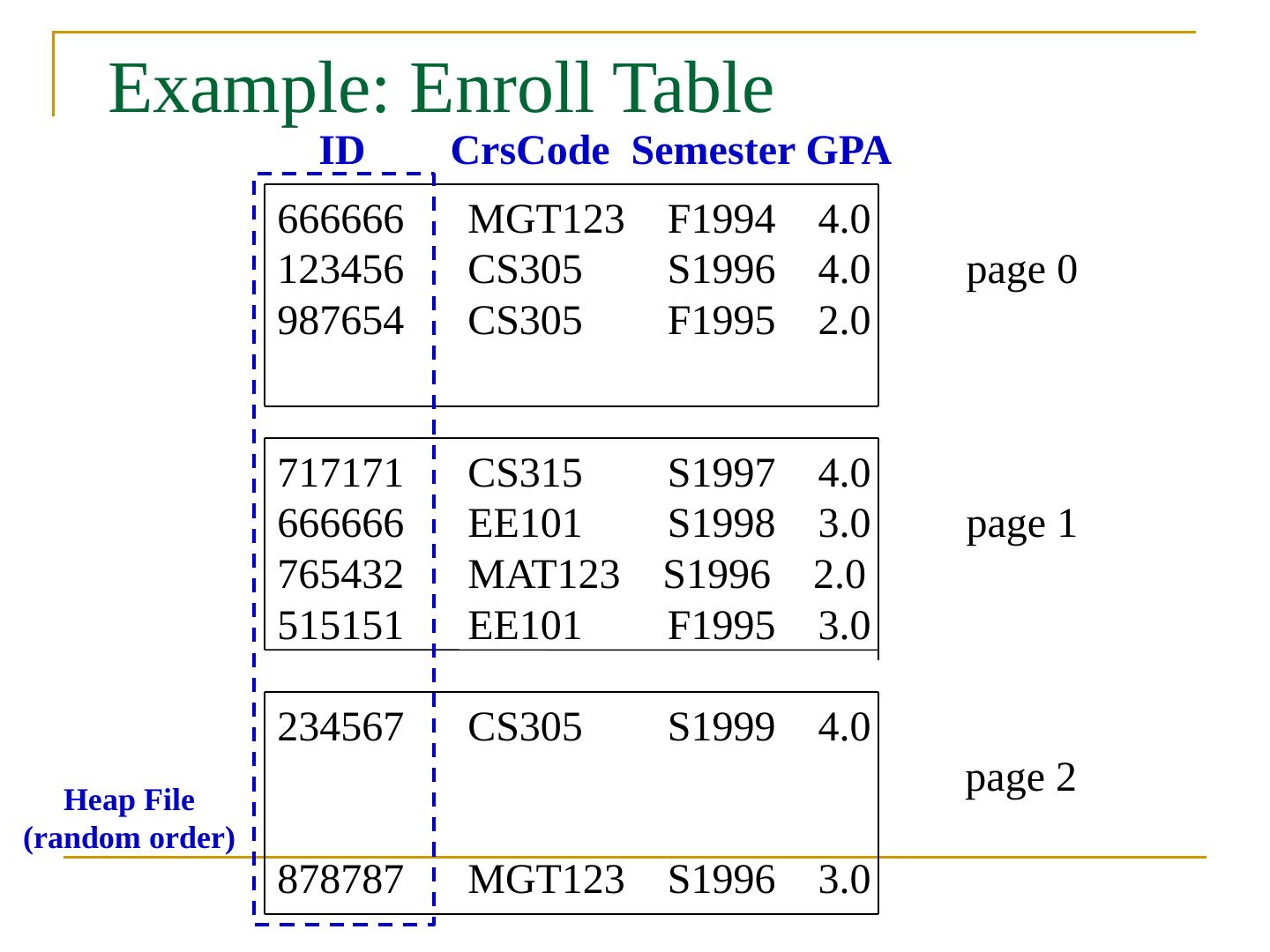
11 .Example: Enroll Table 666666 MGT123 F1994 4.0 123456 CS305 S1996 4.0 page 0 987654 CS305 F1995 2.0 717171 CS315 S1997 4.0 666666 EE101 S1998 3.0 page 1 765432 MAT123 S1996 2.0 515151 EE101 F1995 3.0 234567 CS305 S1999 4.0 page 2 878787 MGT123 S1996 3.0 Heap File (random order) ID CrsCode Semester GPA
12 .Example: Enroll Table 666666 MGT123 F1994 4.0 123456 CS305 S1996 4.0 page 0 987654 CS305 F1995 2.0 717171 CS315 S1997 4.0 666666 EE101 S1998 3.0 page 1 765432 MAT123 S1996 2.0 515151 EE101 F1995 3.0 234567 CS305 S1999 4.0 page 2 878787 MGT123 S1996 3.0 Heap File (random order) ID CrsCode Semester GPA
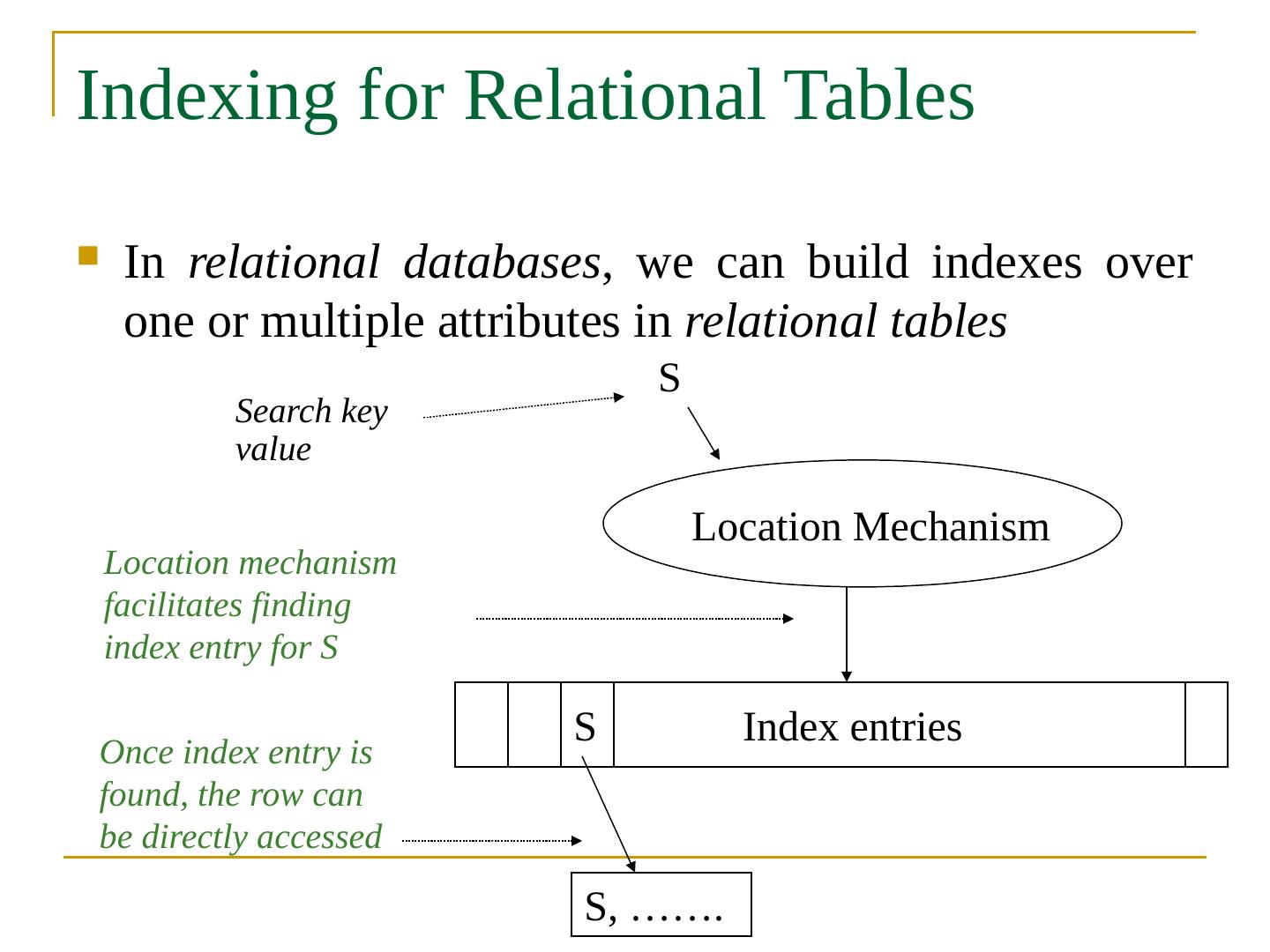
13 .Indexing for Relational Tables In relational databases , we can build indexes over one or multiple attributes in relational tables Location Mechanism Index entries S Search key value Location mechanism facilitates finding index entry for S S S, ……. Once index entry is found, the row can be directly accessed
14 .Indexing for Relational Tables In relational databases , we can build indexes over one or multiple attributes in relational tables Location Mechanism Index entries S Search key value Location mechanism facilitates finding index entry for S S S, ……. Once index entry is found, the row can be directly accessed
15 .Clustered Secondary Index 1 2 3 8 10 1 2 3 8 10
16 .Unclustered Secondary Index 1 2 3 8 10 1 2 3 8 10
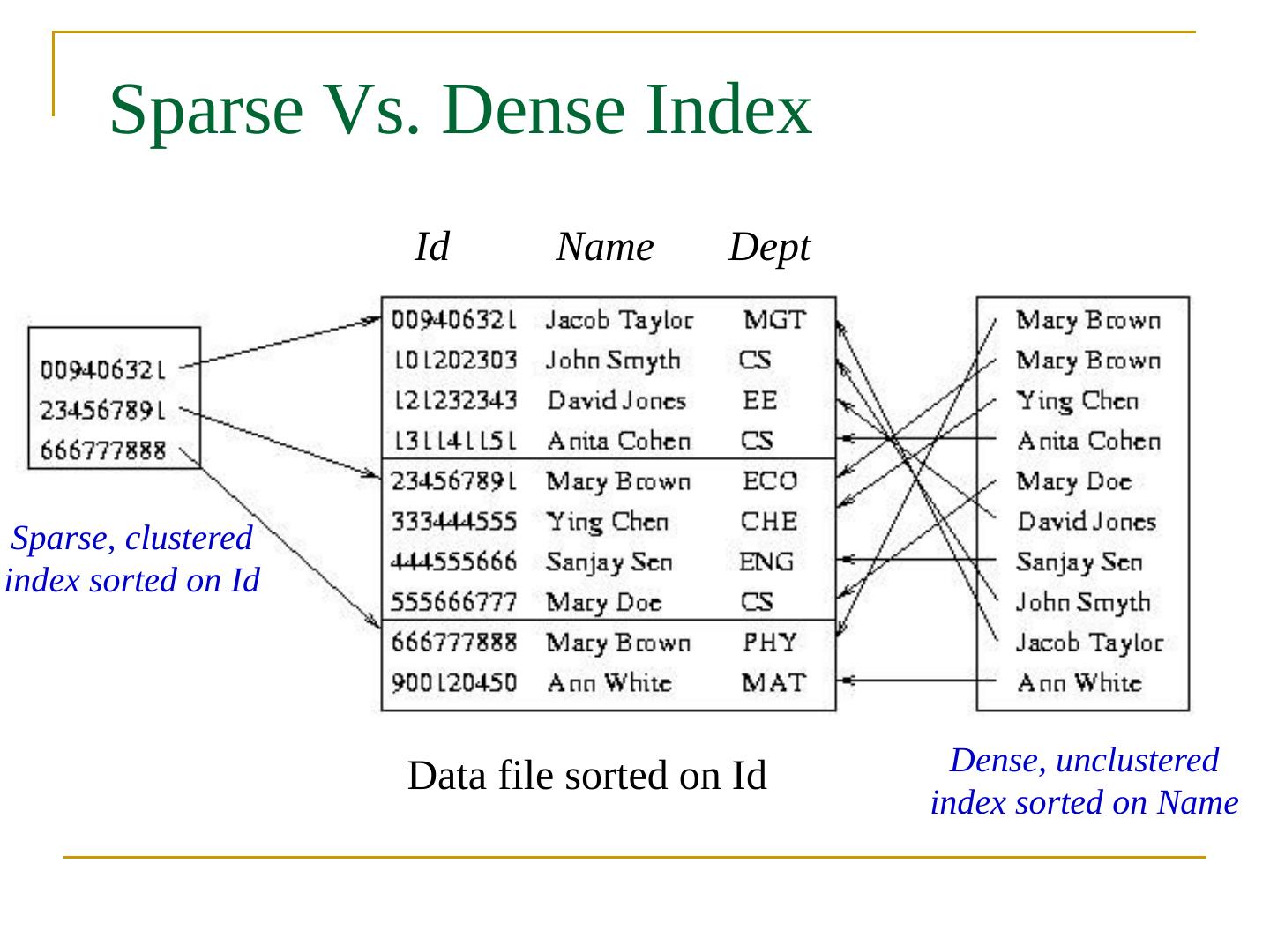
17 .Sparse vs. Dense Index Dense index : has index entry for each data record Unclustered index must be dense Clustered index need not be dense Sparse index : has index entry for each page of data file Sparse index must be clustered
18 .Sparse Vs. Dense Index Sparse, clustered index sorted on Id Dense, unclustered index sorted on Name Data file sorted on Id Id Name Dept
19 .Indexes for Relational Tables Index Sequential Access Method (ISAM ) B + -tree Hashing
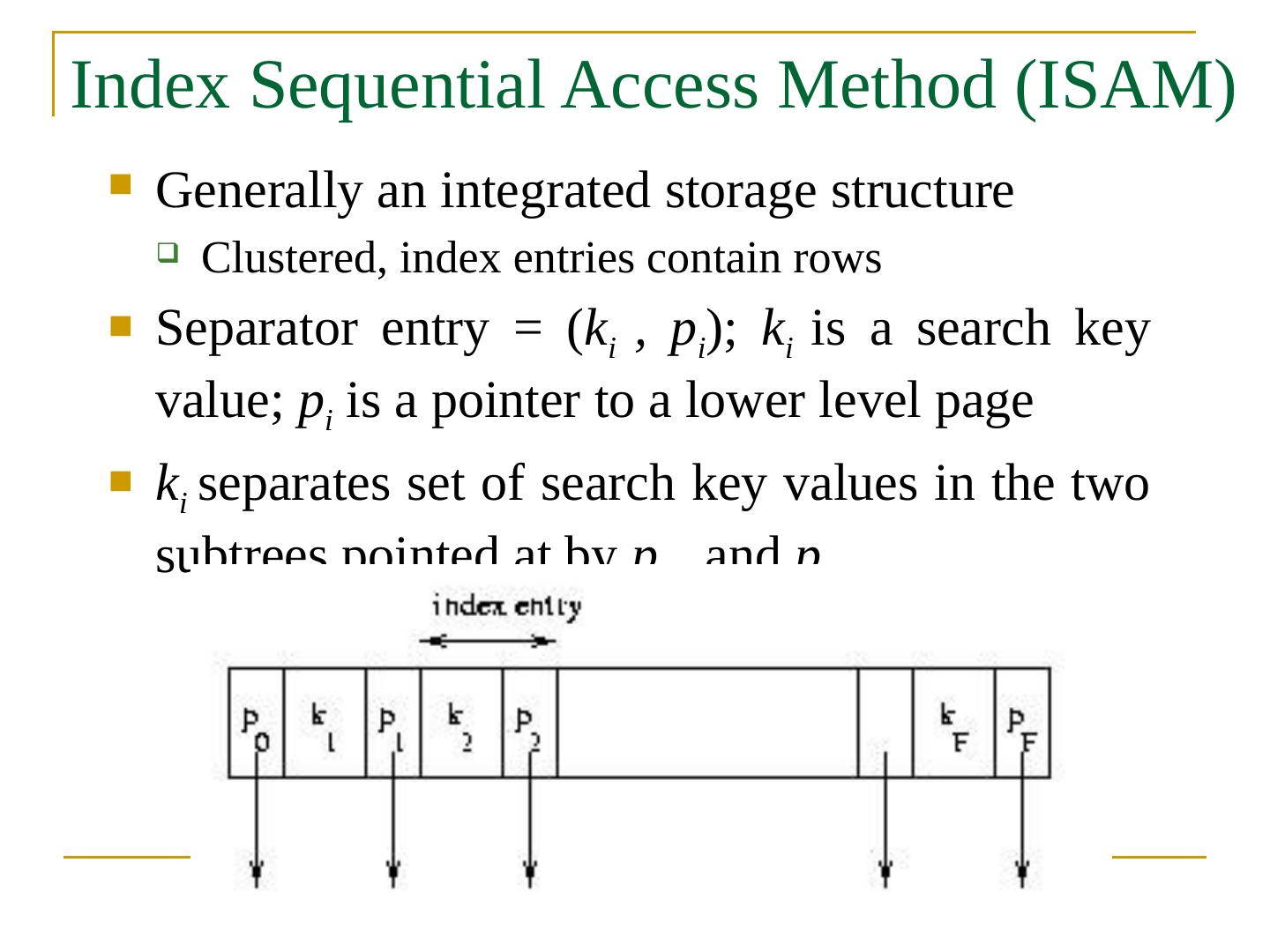
20 .Index Sequential Access Method (ISAM) Generally an integrated storage structure Clustered, index entries contain rows Separator entry = ( k i , p i ); k i is a search key value; p i is a pointer to a lower level page k i separates set of search key values in the two subtrees pointed at by p i-1 and p i.
21 .Example: Index Sequential Access Method Location mechanism
22 .Overflow Chains - Contents of leaf pages change – Row deletion yields empty slot in leaf page – Row insertion can result in overflow leaf page and ultimately overflow chain – Chains can be long, unsorted, scattered on disk – Thus ISAM can be inefficient if table is dynamic
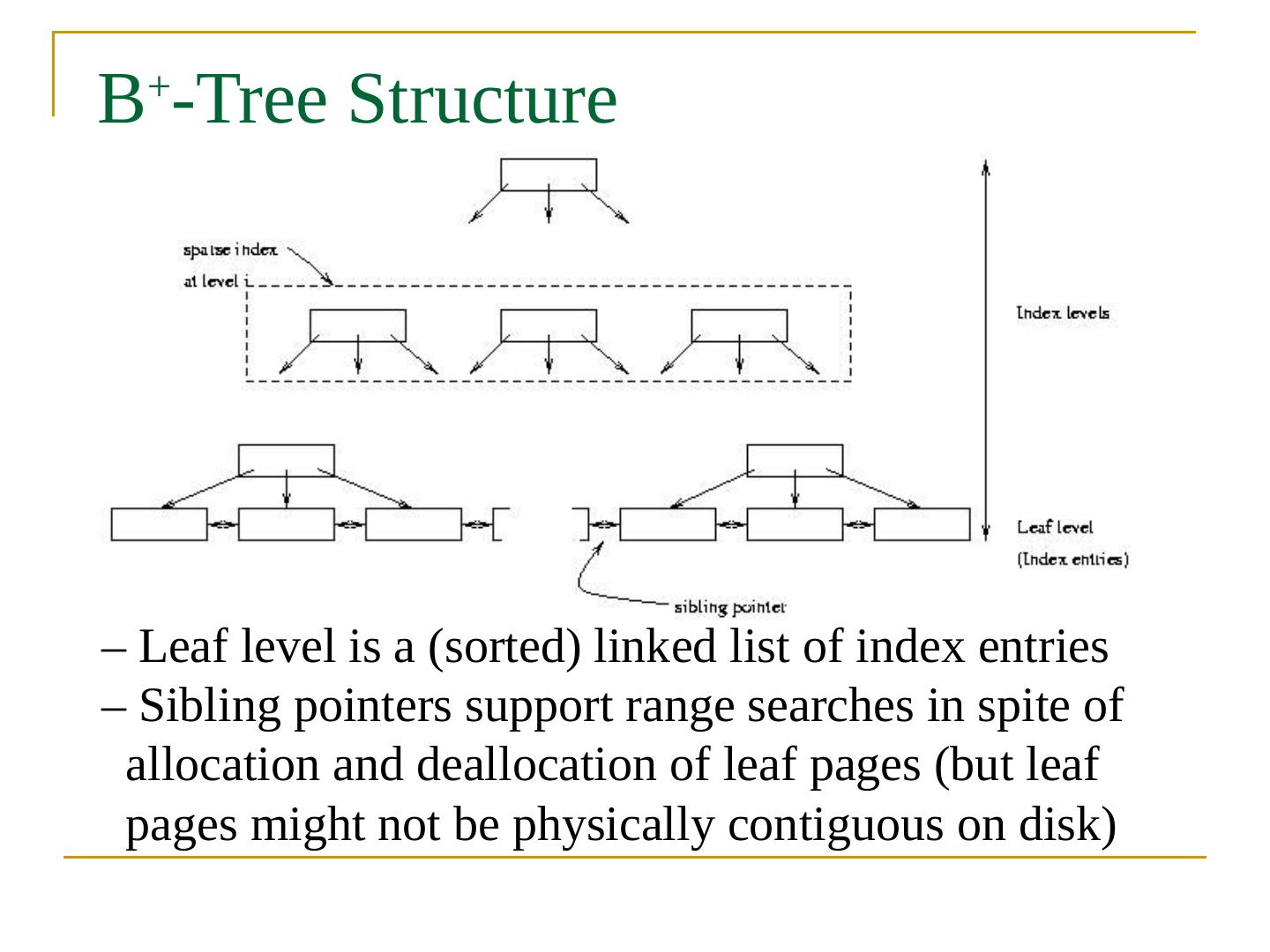
23 .B + -Tree Structure – Leaf level is a (sorted) linked list of index entries – Sibling pointers support range searches in spite of allocation and deallocation of leaf pages (but leaf pages might not be physically contiguous on disk)
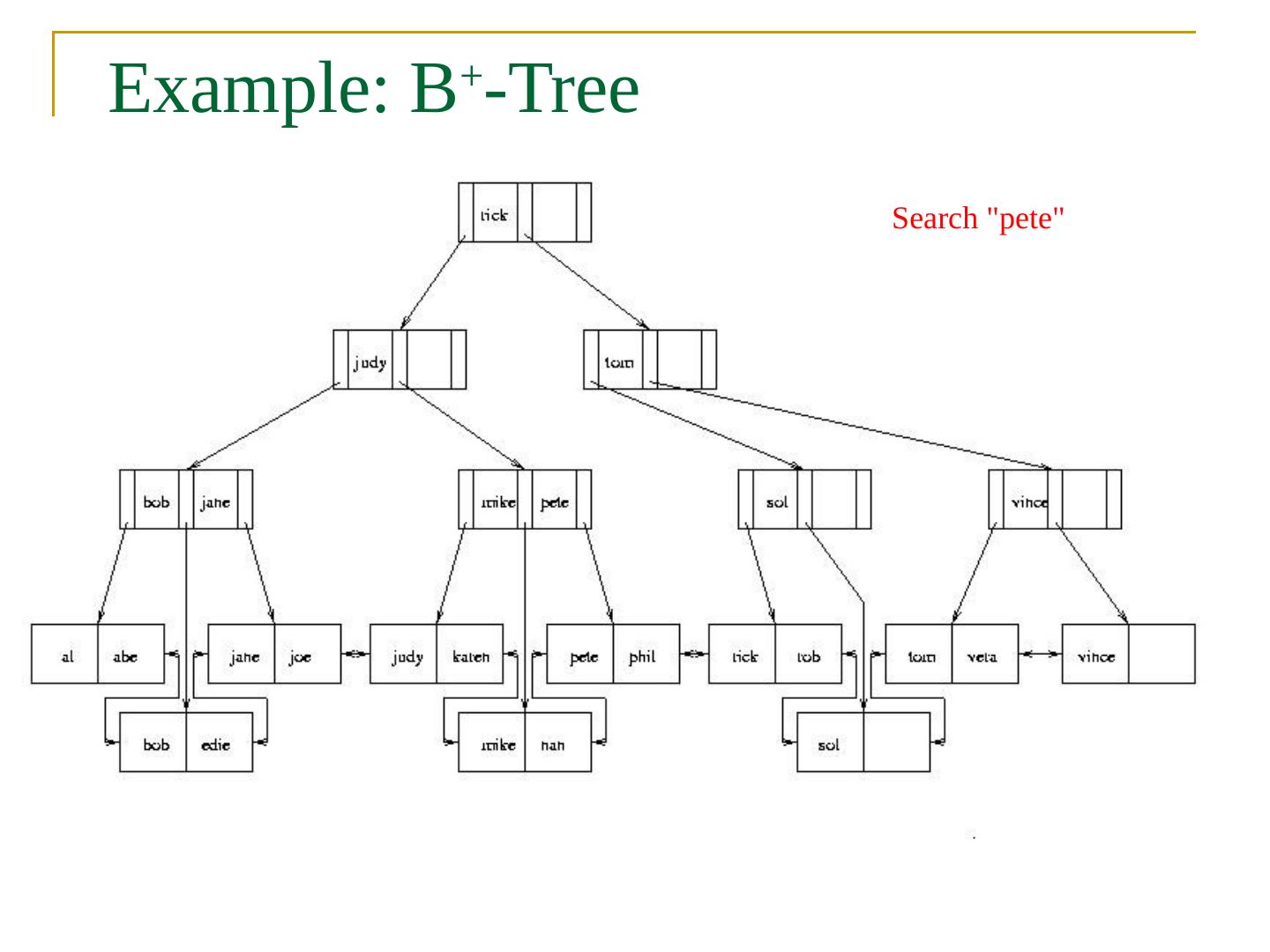
24 .Example: B + -Tree Search " pete "
25 .Example: B + -Tree Search " pete "
26 .Insertion and Deletion in B + Tree Structure of tree changes to handle row insertion and deletion – no overflow chains Tree remains balanced : all paths from root to index entries have same length Algorithm guarantees that the number of separator entries in an index page is between /2 and Hence the maximum search cost is log /2 Q + 1 (with ISAM search cost depends on length of overflow chain)
27 .Handling Insertions - Example - Insert “vince” = 2
28 .Handling Insertions (cont’d) – Insert “vera”: Since there is no room in leaf page: 1. Create new leaf page, C 2. Split index entries between B and C (but maintain sorted order) 3. Add separator entry at parent level = 2
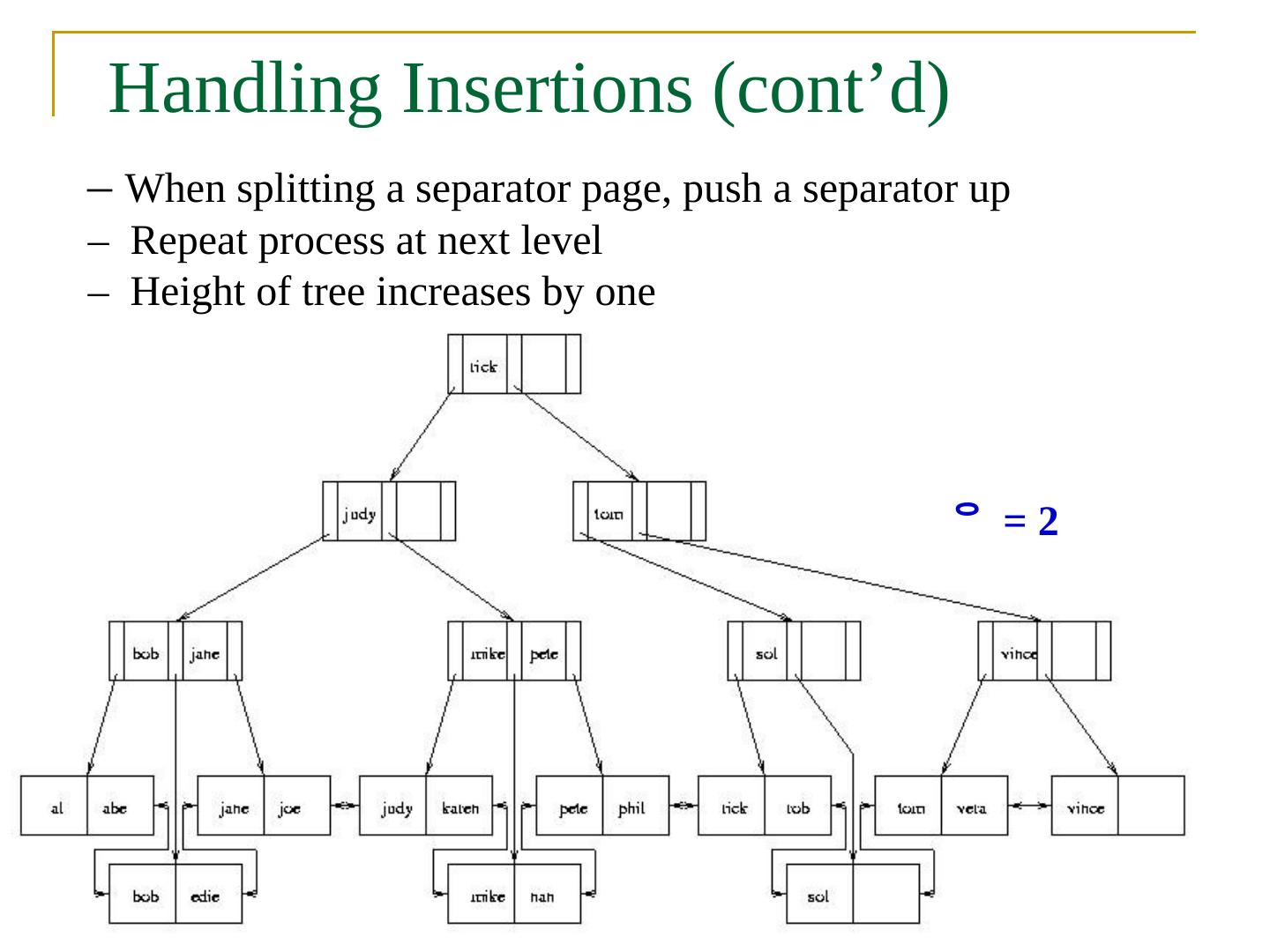
29 .Handling Insertions ( con’t ) – Insert “rob”. Since there is no room in leaf page A: 1. Split A into A1 and A2 and divide index entries between the two (but maintain sorted order) 2. Split D into D1 and D2 to make room for additional pointer 3. Three separators are needed: “sol”, “tom” and “vince” = 2