Data Mining Cluster Analysis Basics - UTC.edu

1 .Data Mining Cluster Analysis Basics From Introduction to Data Mining by Tan , Steinbach, Kumar

2 .What is Cluster Analysis? Finding groups of objects such that the objects in a group will be similar (or related) to one another and different from (or unrelated to) the objects in other groups Inter-cluster distances are maximized Intra-cluster distances are minimized

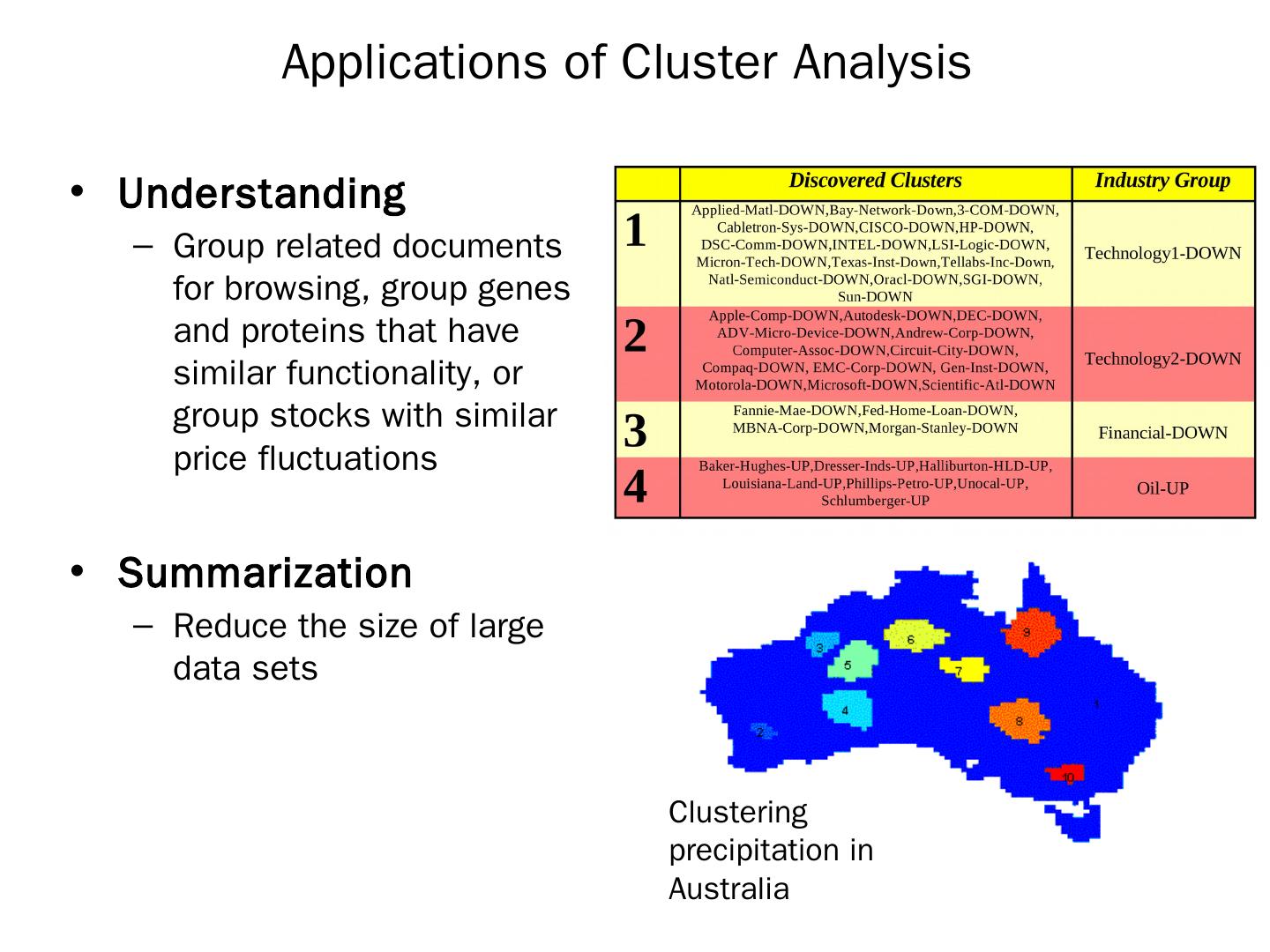
3 .Applications of Cluster Analysis Understanding Group related documents for browsing, group genes and proteins that have similar functionality, or group stocks with similar price fluctuations Summarization Reduce the size of large data sets Clustering precipitation in Australia

4 .What is not Cluster Analysis? Supervised classification Have class label information Simple segmentation Dividing students into different registration groups alphabetically, by last name Results of a query Groupings are a result of an external specification Graph partitioning Some mutual relevance and synergy, but areas are not identical

5 .Notion of a Cluster can be Ambiguous How many clusters? Four Clusters Two Clusters Six Clusters

6 .Types of Clusterings A clustering is a set of clusters Important distinction between hierarchical and partitional sets of clusters Partitional Clustering A division data objects into non-overlapping subsets (clusters) such that each data object is in exactly one subset Hierarchical clustering A set of nested clusters organized as a hierarchical tree

7 .Partitional Clustering Original Points A Partitional Clustering

8 .Hierarchical Clustering Traditional Hierarchical Clustering Non-traditional Hierarchical Clustering Non-traditional Dendrogram Traditional Dendrogram

9 .Other Distinctions Between Sets of Clusters Exclusive versus non-exclusive In non-exclusive clusterings, points may belong to multiple clusters. Can represent multiple classes or ‘border’ points Fuzzy versus non-fuzzy In fuzzy clustering, a point belongs to every cluster with some weight between 0 and 1 Weights must sum to 1 Probabilistic clustering has similar characteristics Partial versus complete In some cases, we only want to cluster some of the data Heterogeneous versus homogeneous Cluster of widely different sizes, shapes, and densities

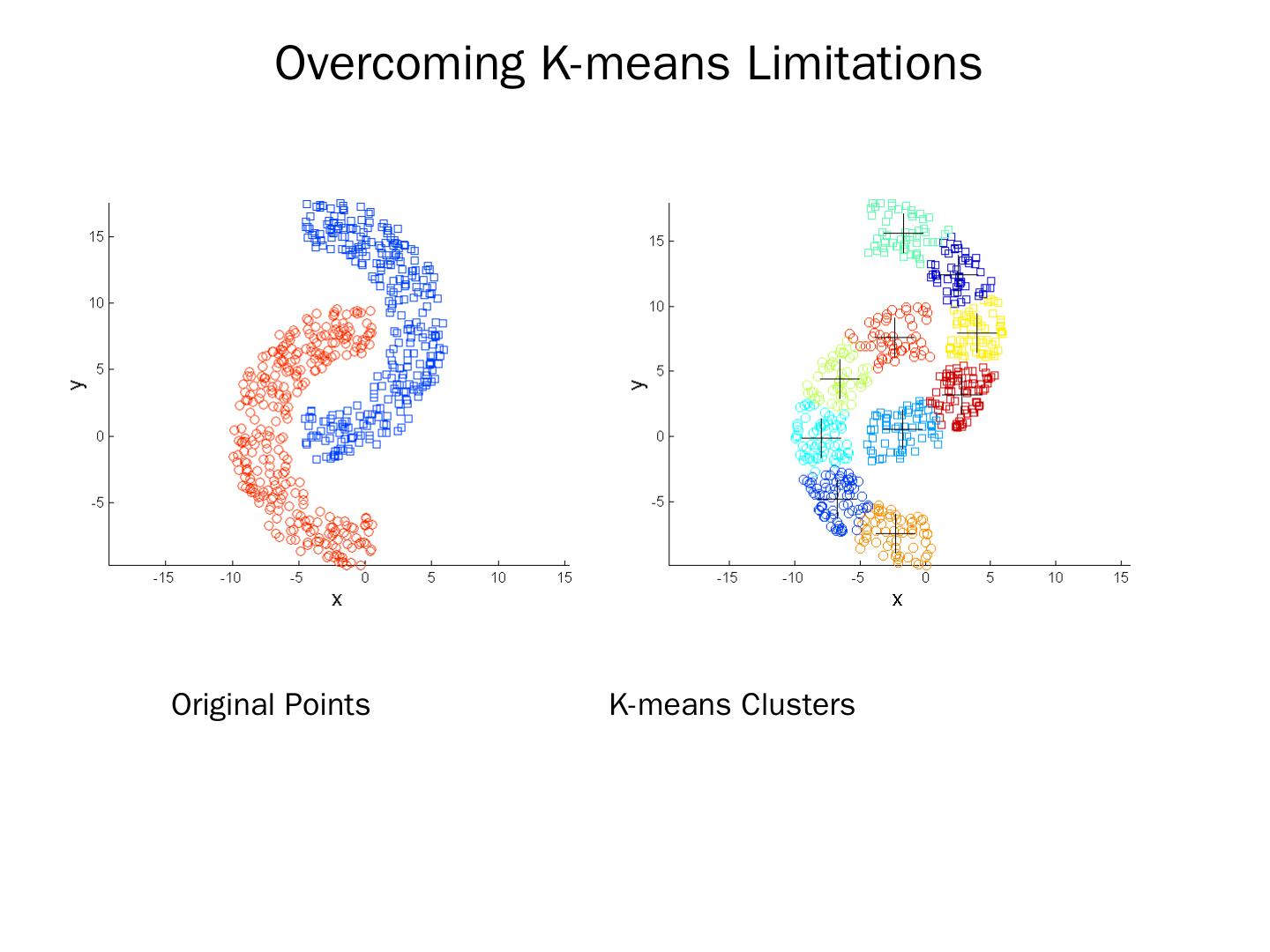
10 .Types of Clusters Well-separated clusters Center-based clusters Contiguous clusters Density-based clusters Property or Conceptual Described by an Objective Function

11 .Types of Clusters: Well-Separated Well-Separated Clusters: A cluster is a set of points such that any point in a cluster is closer (or more similar) to every other point in the cluster than to any point not in the cluster. 3 well-separated clusters

12 .Types of Clusters: Center-Based Center-based A cluster is a set of objects such that an object in a cluster is closer (more similar) to the “center” of a cluster, than to the center of any other cluster The center of a cluster is often a centroid , the average of all the points in the cluster, or a medoid , the most “representative” point of a cluster 4 center-based clusters

13 .Types of Clusters: Contiguity-Based Contiguous Cluster (Nearest neighbor or Transitive) A cluster is a set of points such that a point in a cluster is closer (or more similar) to one or more other points in the cluster than to any point not in the cluster. 8 contiguous clusters

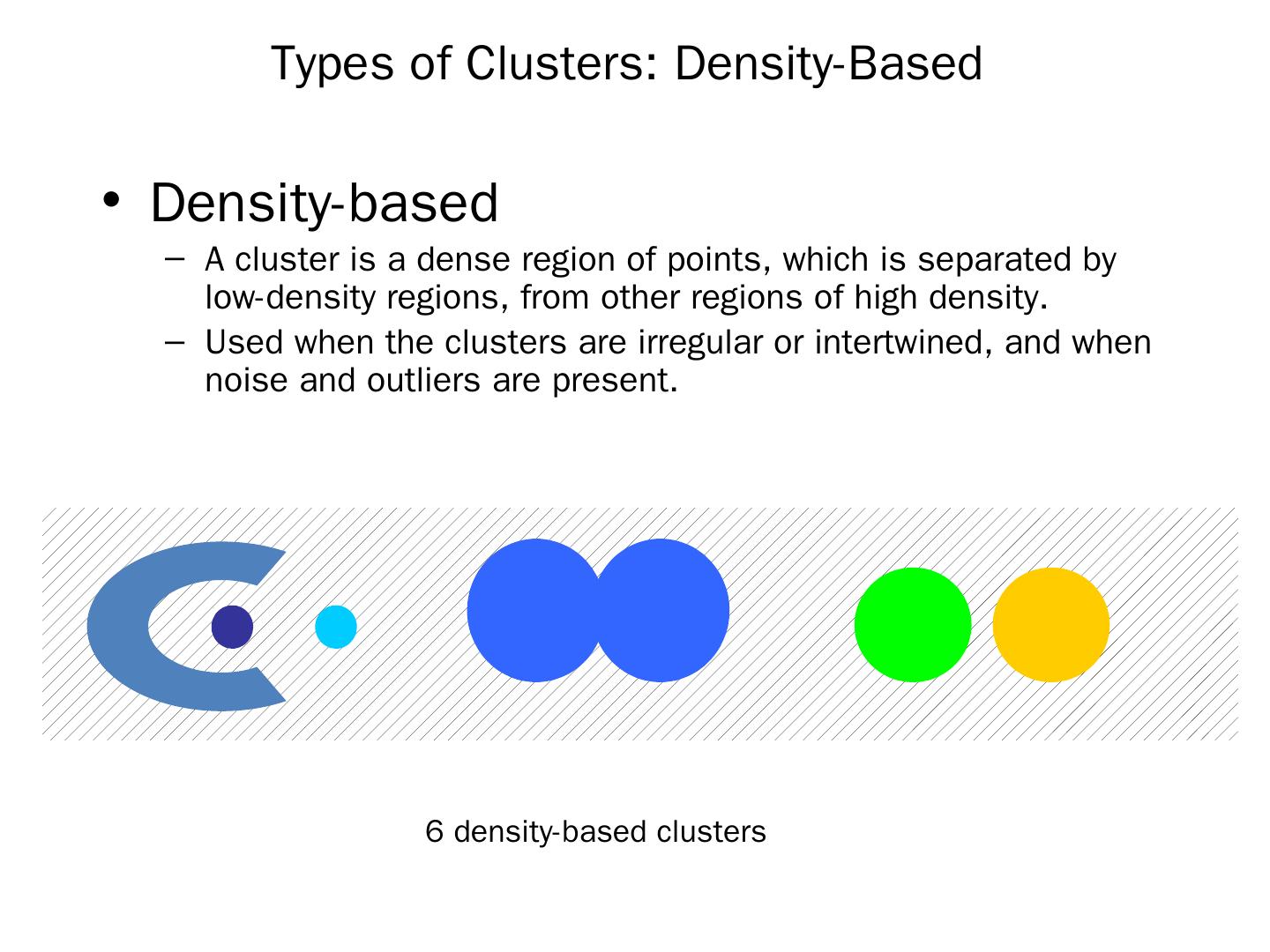
14 .Types of Clusters: Density-Based Density-based A cluster is a dense region of points, which is separated by low-density regions, from other regions of high density. Used when the clusters are irregular or intertwined, and when noise and outliers are present. 6 density-based clusters

15 .Types of Clusters: Conceptual Clusters Shared Property or Conceptual Clusters Finds clusters that share some common property or represent a particular concept. . 2 Overlapping Circles

16 .Types of Clusters: Conceptual Clusters Shared Property or Conceptual Clusters Finds clusters that share some common property or represent a particular concept. . 2 Overlapping Circles

17 .Types of Clusters: Objective Function … Map the clustering problem to a different domain and solve a related problem in that domain Proximity matrix defines a weighted graph, where the nodes are the points being clustered, and the weighted edges represent the proximities between points Clustering is equivalent to breaking the graph into connected components, one for each cluster. Want to minimize the edge weight between clusters and maximize the edge weight within clusters

18 .Characteristics of the Input Data Are Important Type of proximity or density measure This is a derived measure, but central to clustering Sparseness Dictates type of similarity Adds to efficiency Attribute type Dictates type of similarity Type of Data Dictates type of similarity Other characteristics, e.g., autocorrelation Dimensionality Noise and Outliers Type of Distribution

19 .Clustering Algorithms K-means and its variants Hierarchical clustering Density-based clustering

20 .K-means Clustering Partitional clustering approach Each cluster is associated with a centroid (center point) Each point is assigned to the cluster with the closest centroid Number of clusters, K, must be specified The basic algorithm is very simple

21 .K-means Clustering – Details Initial centroids are often chosen randomly. Clusters produced vary from one run to another. The centroid is (typically) the mean of the points in the cluster. ‘Closeness’ is measured by Euclidean distance, cosine similarity, correlation, etc. K-means will converge for common similarity measures mentioned above. Most of the convergence happens in the first few iterations. Often the stopping condition is changed to ‘Until relatively few points change clusters’ Complexity is O( n * K * I * d ) n = number of points, K = number of clusters, I = number of iterations, d = number of attributes

22 .Two different K-means Clusterings Sub-optimal Clustering Optimal Clustering Original Points

23 .Importance of Choosing Initial Centroids

24 .Importance of Choosing Initial Centroids

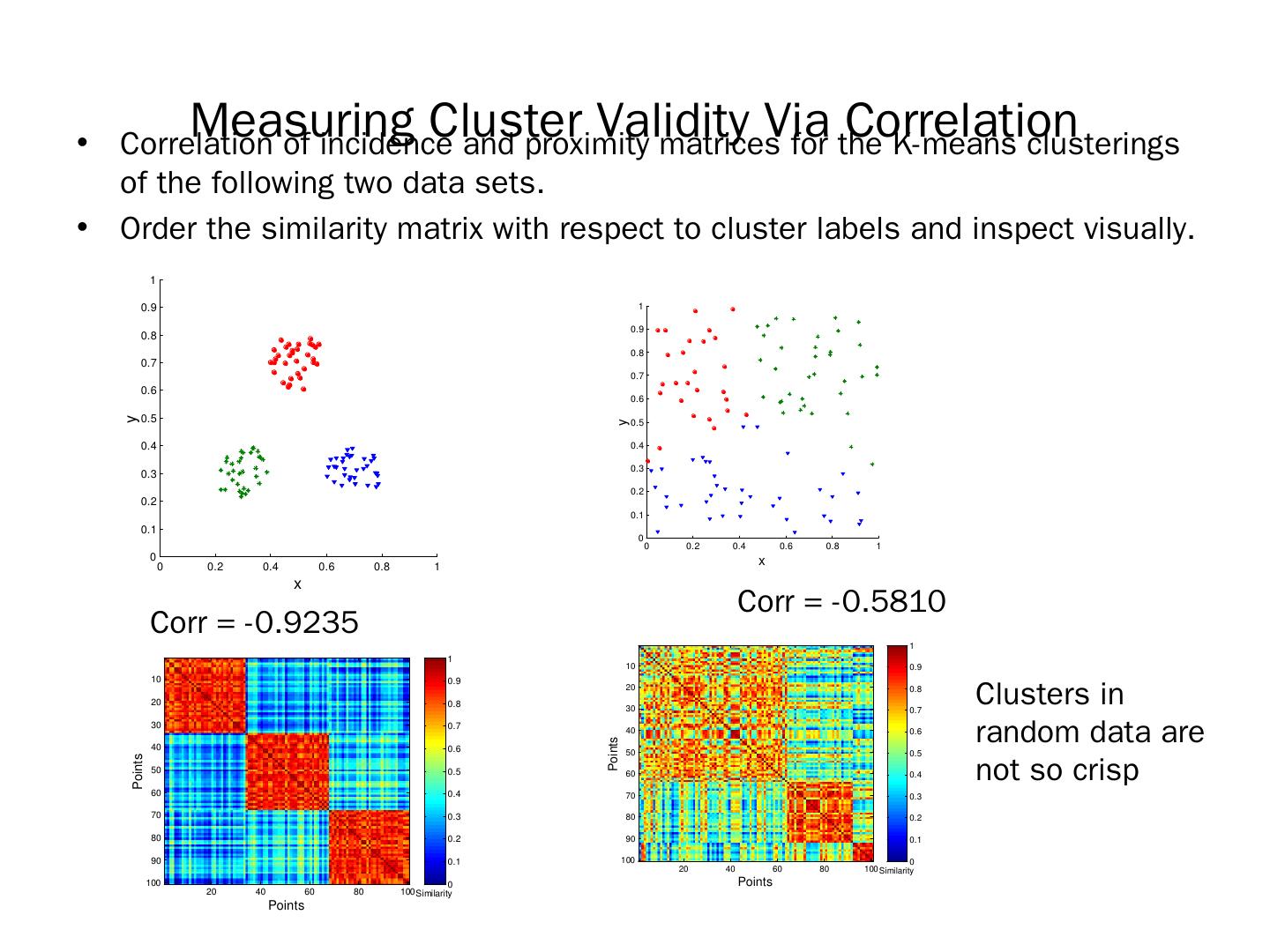
25 .Evaluating K-means Clusters Most common measure is Sum of Squared Error (SSE) For each point, the error is the distance to the nearest cluster To get SSE, we square these errors and sum them. x is a data point in cluster C i and m i is the representative point for cluster C i can show that m i corresponds to the center (mean) of the cluster Given two clusters, we can choose the one with the smallest error One easy way to reduce SSE is to increase K, the number of clusters A good clustering with smaller K can have a lower SSE than a poor clustering with higher K

26 .Importance of Choosing Initial Centroids …

27 .Importance of Choosing Initial Centroids …

28 .Problems with Selecting Initial Points If there are K ‘real’ clusters then the chance of selecting one centroid from each cluster is small. Chance is relatively small when K is large If clusters are the same size, n, then For example, if K = 10, then probability = 10!/10 10 = 0.00036 Sometimes the initial centroids will readjust themselves in ‘right’ way, and sometimes they don’t Consider an example of five pairs of clusters

29 .10 Clusters Example Starting with two initial centroids in one cluster of each pair of clusters