K-means Clustering - MIRLab

1 .K-means Clustering J.-S. Roger Jang ( 張智星 ) jang@mirlab.org http://mirlab.org/jang MIR Lab, CSIE Dept. National Taiwan University 18年9月2 日 

2 .Problem Definition Quiz!  Input A dataset in d-dim. Space X  {x1 , x2 ,  , xn }  m: Number of clusters  Output M cluster centers: C  {c1 , c2 ,  , cm }, m  n  Requirement  The difference between X and C should be as small as p ossible (since we want to use C to represent X) 2/28 

3 .Goal of K-means Clustering  Example of k-meals clustering in 2D 3/28 

4 .Objection Function  Objective function (aka distortion) Quiz!  x c 2 ej  i j xi G j m m m n J ( X ; C , A)   e j      aij xi  c j , where 2 2 xi  c j j 1 j 1 xi G j j 1 i 1 X  {x1 , x2 ,  , xn } : dataset (d  n) C  {c1 , c2 ,  , cm } : cluster centers (d  m, m  n) A : assignment matrix (n  m) m aij  {0,1}, aij  1 iff xi  G j , with  aij  1, i j 1  No of parameters: d*m (for C) plus n*m (for A, with constraints)  NP-hard problem if exact solution is required. 4/28 

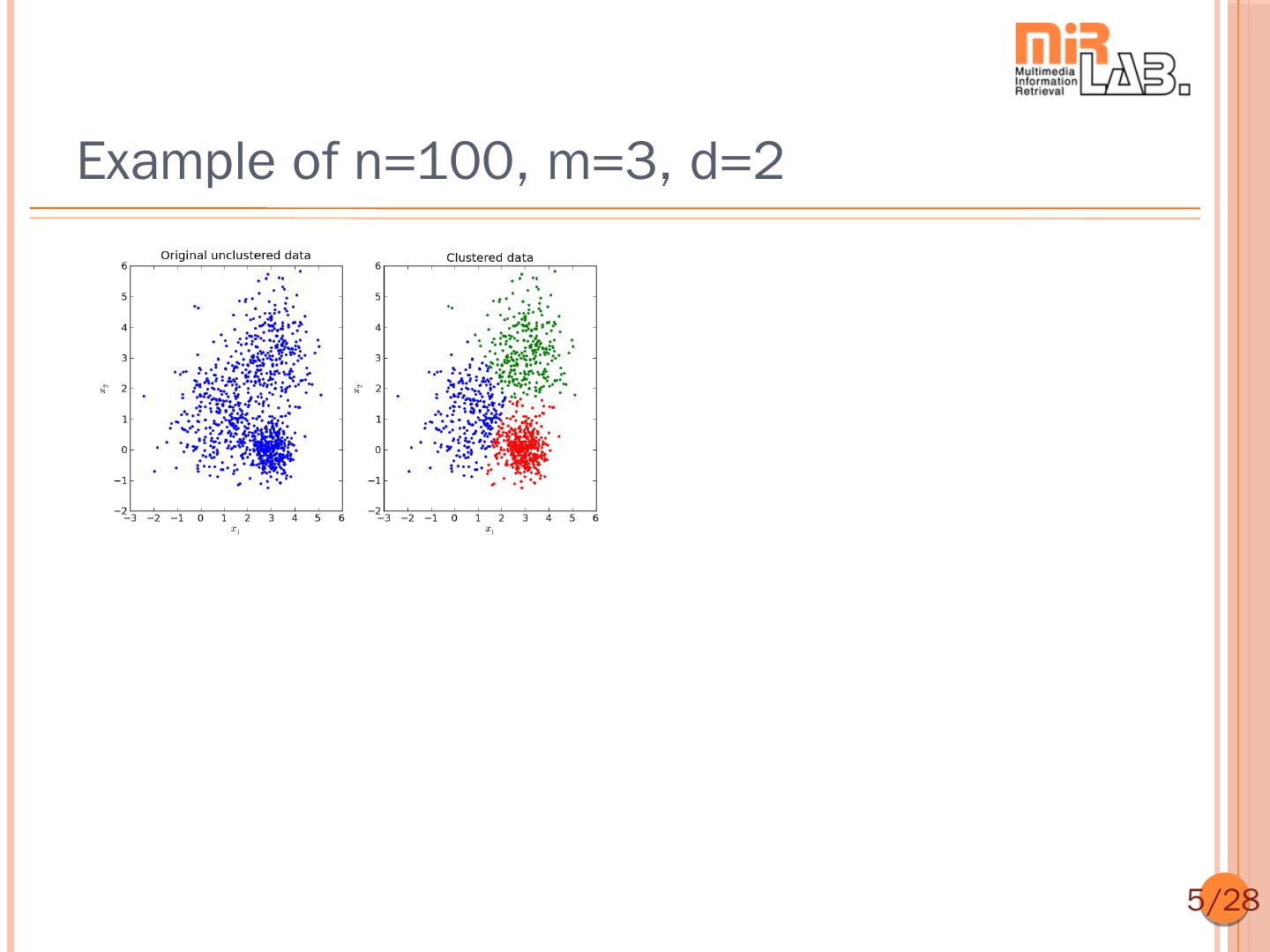
5 .Example of n=100, m=3, d=2 5/28 

6 .Strategy for Minimizing the Objective Functio n  Observation  J(X;C, A) is parameterized by C and A  Joint optimization is hard, but separate optimization with respective to C and A is easy  Strategy AKA “coordinate optimization”  Fix C and find the best A to minimize J(X; C, A)  Fix A and find the best C to minimize J(X; C, A)  Repeat the above two steps until convergence 6/28 

7 .Example of Coordinate Optimization f ( x, y )  x 2  y 2  y  1  x y 2  1  y 2  1 Quiz! f ( x, y ) y2 1  2 x y  y  1   y  1  0  x   2 2 x 2 y 2  y  1 f ( x, y ) x 2  x 2  2 y  1  x 2 y   2 y  0  y   y 2 x 2  x  1 ezmeshc(@(x,y) x.^2.*(y.^2+y+1)+x.*(y.^2-1)+y.^2-1) 7/28 

8 .Task 1: How to Find Assignment A?  Goal  Find A to minimize J(X; C, A) with fixed C  Fact  Analytic (close-form) solution exists  1 if j  arg min x  c 2 aˆij   q i q Quiz!  0, otherwise Aˆ  arg min J ( X ; C , A)  J ( X ; C , A)  J ( X ; C , Aˆ ), C A 8/28 

9 .Task 2: How to Find Centers in C?  Goal  Find C to minimize J(X; C, A) with fixed A  Fact  Analytic (close-form) solution exists: n Quiz! a x ij i cˆ j  i 1 n a i 1 ij Cˆ  arg min J ( X ; C , A)  J ( X ; C , A)  J ( X ; Cˆ , A), A C 9/28 

10 . Quiz! Algorithm 1. Initialize Start with initial centers  Select initial centers in C 2. Find clusters (assignment) in A  Assign each point to its nearest centers  That is, find A to minimize J(X; C, A) with fixed C 3. Find centers in C  Compute each cluster centers as the mean of the cluster’s d ata  That is, find C to minimize J(X; C, A) with fixed A 4. Stopping criterion  Stop if “change is small”. Otherwise go back to step 2. 10 /28 

11 .Another Algorithm Quiz! 1. Initialize  Select Start with initial clusters initial clusters in A 2. Find centers in C  Compute each cluster centers as the mean of the cluster’s data  That is, find C to minimize J(X; C, A) with fixed A 3. Find clusters (assignment) in A  Assign each point to its nearest centers  That is, find A to minimize J(X; C, A) with fixed C 4. Stopping criterion  Stop if “change is small”. Otherwise go back to step 2. 11 /28 

12 . 18年9月2日 More about Stopping Criteria  Possible stopping criteria  Distortionimprovement over previous iteration is small  No more change in clusters  Change in cluster centers is small  Fact  Convergence Quiz! is guarantee since J is reduced repeatedly.  For algorithm that starts with initial centers: J ( X ; C1 , _)  J ( X ; C1 , A1 )  J ( X ; C2 , A1 )  J ( X ; C2 , A2 )  J ( X ; C3 , A2 )  J ( X ; C3 , A3 )    J ( X ; C1 )  J ( X ; C2 )  J ( X ; C3 )   12 /28 

13 . 18年9月2日 Properties of K-means Clustering  Properties  Always converges  No guarantee to converge to global minimum  To increase the likelihood of reaching the global minimu m  Start with various sets of initial centers  Start with sensible choice of initial centers  Potential distance functions  Euclidean distance  Texicab distance  How to determine the best choice of k  Cluster validation 13 /28 

14 . 18年9月2日 Snapshots of K-means Clustering 14 /28 

15 . 18年9月2日 Demos of K-means Clustering  Required toolboxes  Utility Toolbox  Machine Learning Toolbox  Demos  kMeansClustering.m  vecQuantize.m  Center splitting to reach 2p clusters 15 /28 

16 . 18年9月2日 Demo of K-means Clustering  Required toolboxes 0.8 0.8  Utility Toolbox 0.6 0.6 0.4 0.4  Machine Learning Toolbox 0.2 0.2 Input 2 0 0 Demos ­0.2 ­0.2  ­0.4 ­0.4  kMeansClustering.m ­0.6 ­0.6 ­0.8 ­0.8  vecQuantize.m ­0.8 ­0.6 ­0.4 ­0.2 0 0.2 0.4 0.6 0.8 ­0.8 ­0.6 ­0.4 ­0.2 0 Input 1 0.2 0.4 0.6 0.8  Center splitting to reach 2p clusters 16 /28 

17 . 18年9月2日 Application: Image Compression  Goal  Convert an image from true colors to index colors with mi nimum distortion  Steps  Collectpixel data from a true-color image  Perform k-means clustering to obtain cluster centers as t he indexed colors  Compression ratio Quiz! before  m * n * 3 * 8 bits after  m * n * log 2  c   c * 3 * 8 bits before m * n *3*8 24 24     after m * n * log 2  c   c * 3 * 8 log  c   24c log 2  c  2 m*n 17 /28 

18 . 18年9月2日 True-color vs. Index-color Images Quiz!  True-color image  Index-color image  Each pixel is represe  Each pixel is represe nted by a vector of 3 nted by an index into components [R, G, B]. a color map of 2b col  Advantage ors.  More colors  Advantage  Less storage 18 /28 

19 .Example of Image Compression 18年9月2日  Date: 1998/04/05  Dimension: 480x640  Raw data size: 480*64 0*3 bytes = 900KB  File size: 49.1KB  Compression ratio = 9 00/49.1 = 18.33 19 /28 

20 .Example of Image Compression 18年9月2日  Date: 2015/11/01  Dimension: 3648x5472  Raw data size: 3648*5 472*3 bytes = 57.1MB  File size: 3.1MB  Compression ratio = 5 7.1/3.1 = 18.42 20 /28 

21 . 18年9月2日 Image Compression Using K-Means Clusteri ng  Some quantities of the k-means clustering n = 480x640 = 307200 (no of vectors to be clustered)  d = 3 (R, G, B)  m = 256 (no. of clusters) 21 /28 

22 . 18年9月2日 Example: Image Compression Using K-me ans 18年9月2日 22 22 /28 

23 . 18年9月2日 Example: Image Compression Using K-me ans 18年9月2日 23 23 /28 

24 . 18年9月2日 Indexing Techniques  Indexing of pixels for a 2x3x3 image 1 1 1  1 2 3 4 5 6 3 75 97 1  7 8 910 11 12 1 1 1 1 31 5  4 86 218 41 6  13 14 15 16 17 18 0 2  Related command: reshape X = imread('annie19980405.jpg'); image(X); [m, n, p]=size(X); index=reshape(1:m*n*p, m*n, 3)'; data=double(X(index)); 24 /28 

25 . 18年9月2日 Code Example X = imread('annie19980405.jpg'); image(X) [m, n, p]=size(X); index=reshape(1:m*n*p, m*n, 3)'; data=double(X(index)); maxI=6; for i=1:maxI centerNum=2^i; fprintf('i=%d/%d: no. of centers=%d\n', i, maxI, centerNum); center=kMeansClustering(data, centerNum); distMat=distPairwise(center, data); [minValue, minIndex]=min(distMat); X2=reshape(minIndex, m, n); map=center'/255; figure; image(X2); colormap(map); colorbar; axis image; drawnow; end 25 /28 

26 . 18年9月2日 Extensions to Block-based Image Compressi on  Extensions to image data compression via clusterin g  Use qxq blocks as the unit for VQ (see exercise)  Smart indexing by creating the indices of the blocks of page 1 first.  True-color image display (No way to display the compressed image as an index-color image)  Use separate before  m * ncode books for RGB * 3 * 8 bits Quiz! m n after  * * log 2  c   c * q 2 * 3 * 8 bits q q before m * n * 3*8 24q 2    after m n 24cq 4 * * log 2  c   c * q * 3 * 8 log 2  c   2 q q m*n 26 /28 

27 . 18年9月2日 Extension to L1-norm  Use L1-norm instead of L2-norm in the objective func tion  Optimization strategy  Same as k-means clustering, except that the centers are Quiz! found by the median operator  Advantage Quiz!  Less susceptible to outliers 27 /28 

28 . 18年9月2日 Extension to Circle Fitting  Find circles via k-means clustering 4 3 2 1 0 ­1 ­2 ­1 0 1 2 3 4 28 /28